【数据结构与算法】——图(一)
前言
这部分内容只是基于学校和网上整理,后续在C++学习后会在C++或数据结构专栏更新
本文包括图的基本概念、两种存储方式(邻接矩阵、邻接表)
本人其他博客:https://blog.csdn.net/2401_86940607
源代码见gitte: https://gitee.com/mozhengy
图
- 前言
- 正文
- 1.图的基本概念
- 1.1 图的定义
- 1.2 关键要素与术语
- 1. 有向图
- 2. 无向图
- 3. 简单图
- 4. 多重图
- 5. 完全图(简单完全图)
- 6. 子图
- 7. 连通、连通图与连通分量
- 8. 强连通图与强连通分量
- 9. 生成树与生成森林
- 10. 顶点的度、入度与出度
- 思维导图总结
- 2 图的存储方式与基本运算算法
- 2.1 邻接矩阵
- 1. 邻接矩阵的定义
- 2. 代码实现解析
- 3. 时间复杂度与空间复杂度
- 4. 邻接矩阵的优缺点
- 5. 代码运行示例
- 2.2 邻接表
- 1.邻接表的定义
- 2. 存储结构组成
- 3. 无向图与有向图的存储方式
- 4. 顶点度的计算
- 5. 优缺点对比
- 总结
正文
1.图的基本概念
1.1 图的定义
图(Graph)是由顶点的有穷非空集合 V V V 和顶点之间边的集合 E E E 组成,记为 G = ( V , E ) G=(V, E) G=(V,E)。其中:
- 顶点集合 V V V:图的基本元素,必须包含至少一个顶点(即 ∣ V ∣ ≥ 1 |V| \geq 1 ∣V∣≥1)。
- 边集合 E E E:描述顶点之间的关系,每条边连接两个顶点。边可以是无向的(如 ( v i , v j ) (v_i, v_j) (vi,vj))或有向的(如 ⟨ v i , v j ⟩ \langle v_i, v_j \rangle ⟨vi,vj⟩,称为弧,其中 v i v_i vi 是弧尾, v j v_j vj 是弧头)。
1.2 关键要素与术语
1. 有向图
若 E E E 是有向边(也称弧)的有限集合,则称图 G G G 为有向图。
- 弧是顶点的有序对,记为 ⟨ v , w ⟩ \langle v, w \rangle ⟨v,w⟩,其中:
- v v v 称为弧尾, w w w 称为弧头。
- ⟨ v , w ⟩ \langle v, w \rangle ⟨v,w⟩ 表示从顶点 v v v 到 w w w 的弧,称 v v v 邻接到 w w w,或 w w w 邻接自 v v v。
示例:
图 G 1 G_1 G1 的定义与图示如下:
G 1 = ( V 1 , E 1 ) , V 1 = { 1 , 2 , 3 } , E 1 = { ⟨ 1 , 2 ⟩ , ⟨ 2 , 1 ⟩ , ⟨ 2 , 3 ⟩ } G_1 = (V_1, E_1), \quad V_1 = \{1, 2, 3\}, \quad E_1 = \{\langle1,2\rangle, \langle2,1\rangle, \langle2,3\rangle\} G1=(V1,E1),V1={1,2,3},E1={⟨1,2⟩,⟨2,1⟩,⟨2,3⟩}
2. 无向图
若 E E E 是无向边(简称边)的有限集合,则称图 G G G 为无向图。
- 边是顶点的无序对,记为 ( v , w ) (v, w) (v,w) 或 ( w , v ) (w, v) (w,v)。
- 顶点 v v v 和 w w w 互为邻接点,边 ( v , w ) (v, w) (v,w) 依附于这两个顶点。
示例:
图 G 2 G_2 G2 的定义与图示如下:
G 2 = ( V 2 , E 2 ) , V 2 = { 1 , 2 , 3 , 4 } , E 2 = { ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 4 ) } G_2 = (V_2, E_2), \quad V_2 = \{1, 2, 3, 4\}, \quad E_2 = \{(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)\} G2=(V2,E2),V2={1,2,3,4},E2={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
3. 简单图
若图 G G G 满足: 1. 不存在重复边; 2. 不存在顶点到自身的边(自环),
则称 G G G 为简单图。
数据结构中默认讨论简单图。
4. 多重图
若图 G G G 中允许: 1. 两个顶点间存在多条边; 2. 顶点通过边与自身关联(自环),
则称 G G G 为多重图。
5. 完全图(简单完全图)
无向完全图:任意两顶点间均有边,边数为 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)。 有向完全图:任意两顶点间有方向相反的两条弧,弧数为 n ( n − 1 ) n(n-1) n(n−1)。
无向完全图(3个顶点,3条边)
6. 子图
设有图 G = ( V , E ) G = (V, E) G=(V,E) 和 G ′ = ( V ′ , E ′ ) G' = (V', E') G′=(V′,E′),若满足:
V ′ ⊆ V V' \subseteq V V′⊆V 且 E ′ ⊆ E E' \subseteq E E′⊆E,则称 G ′ G' G′ 是 G G G 的子图。
若 V ′ = V V' = V V′=V,则称 G ′ G' G′ 为 G G G 的生成子图。
7. 连通、连通图与连通分量
连通:无向图中顶点 v v v 到 w w w 有路径。
连通图:任意两顶点均连通的图。
连通分量:无向图中的极大连通子图。
非连通图特性:若顶点数为 n n n,边数 < n − 1 < n-1 <n−1,则必为非连通图。
8. 强连通图与强连通分量
强连通:有向图中顶点 v v v 和 w w w 双向可达。
强连通图:任意两顶点均强连通的图。
强连通分量:有向图中的极大强连通子图。
9. 生成树与生成森林
生成树:连通图的极小连通子图,包含所有顶点且边数为 n − 1 n-1 n−1。
生成森林:非连通图中各连通分量的生成树的集合。
生成树(4个顶点,3条边)
10. 顶点的度、入度与出度
无向图:顶点 v v v 的度 T D ( v ) TD(v) TD(v) 为依附于它的边数。
∑ i = 1 n T D ( v i ) = 2 e (每条边贡献2度) \sum_{i=1}^{n} TD(v_i) = 2e \quad \text{(每条边贡献2度)} i=1∑nTD(vi)=2e(每条边贡献2度)
有向图:
- 入度 I D ( v ) ID(v) ID(v):以 v v v 为终点的弧数。
- 出度 O D ( v ) OD(v) OD(v):以 v v v 为起点的弧数。
- 总度 T D ( v ) = I D ( v ) + O D ( v ) TD(v) = ID(v) + OD(v) TD(v)=ID(v)+OD(v)。
∑ i = 1 n I D ( v i ) = ∑ i = 1 n O D ( v i ) = e \sum_{i=1}^{n} ID(v_i) = \sum_{i=1}^{n} OD(v_i) = e i=1∑nID(vi)=i=1∑nOD(vi)=e
思维导图总结

2 图的存储方式与基本运算算法
2.1 邻接矩阵
这种算法比较简单,适合稠密图
1. 邻接矩阵的定义
邻接矩阵(Adjacency Matrix) 是图的两种主要存储结构之一,通过二维数组表示顶点之间的连接关系。具体定义如下:
- 顶点集合:用一维数组
vexs[]存储顶点信息。 - 边集合:用二维数组
arc[][]存储边的信息。
对于无权图:
arc[i][j] = 1表示顶点 v i v_i vi 和 v j v_j vj 之间有边。
arc[i][j] = 0表示无边。
对于带权图(网):
arc[i][j] = weight表示边的权值。
arc[i][j] = INF表示不可达(通常用极大值如65535表示)。
无向图 vs 有向图:
无向图的邻接矩阵是对称矩阵(arc[i][j] = arc[j][i])。
-有向图的邻接矩阵可能不对称。
2. 代码实现解析
1 数据结构定义
#define MAXVEX 100 // 最大顶点数
#define INF 65535 // 不可达标记
#define DIRECTED true // 是否为有向图typedef struct {VertexType vexs[MAXVEX]; // 顶点表EdgeType arc[MAXVEX][MAXVEX]; // 邻接矩阵int vexNum, edgeNum; // 顶点数、边数
} MGraph;
vexs[]:存储顶点名称(如字符'A','B')。arc[][]:存储边的权值,初始值为INF。vexNum,edgeNum:记录图的顶点数和边数。
2 创建邻接矩阵
int Graph_Create(MGraph& G) {// 输入顶点数和边数printf("请输入顶点数:");scanf("%d", &G.vexNum);printf("请输入边数:");scanf("%d", &G.edgeNum);// 初始化顶点表for (int i = 0; i < G.vexNum; i++) {printf("请输入第 %d 个的顶点名称: ", i + 1);scanf(" %c", &G.vexs[i]);}// 初始化邻接矩阵为INFfor (int i = 0; i < G.vexNum; i++) {for (int j = 0; j < G.vexNum; j++) {G.arc[i][j] = INF;}}// 输入边信息printf("下标为 -1 -1 则退出创建边\n");for (int i = 0; i < G.edgeNum; i++) {int vi, vj, weight;printf("请输入要创建边的下标 v1 v2 ");scanf("%d %d", &vi, &vj);if (vi == -1 && vj == -1) break;printf("请输入边为[%d][%d]的权值 weight = ", vi, vj);scanf("%d", &weight);G.arc[vi][vj] = weight;if (!DIRECTED) { // 无向图需对称赋值G.arc[vj][vi] = weight;}}return 0;
}
关键步骤说明:
- 输入顶点和边数:确定图的规模。
- 初始化顶点表:按顺序存储顶点名称。
- 初始化邻接矩阵:将所有边的权值设为
INF。 - 填充边信息:根据输入的顶点下标和权值更新矩阵。
- 如果是无向图(
DIRECTED=false),需对称赋值arc[vj][vi] = weight。
- 如果是无向图(
3 打印邻接矩阵
void Graph_Show(MGraph G) {// 打印顶点名称printf("顶点表: ");for (int i = 0; i < G.vexNum; i++)printf("%c ", G.vexs[i]);printf("\n");// 打印邻接矩阵printf("邻接矩阵:\n");for (int i = 0; i < G.vexNum; i++) {for (int j = 0; j < G.vexNum; j++) {if (G.arc[i][j] == INF) printf("%6s", "∞");else printf("%6d", G.arc[i][j]);}printf("\n");}
}
3. 时间复杂度与空间复杂度
| 操作 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 创建邻接矩阵 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) |
| 判断边是否存在 | O ( 1 ) O(1) O(1) | - |
| 遍历所有邻接点 | O ( n ) O(n) O(n) | - |
- 适用场景:适合稠密图(边数接近顶点数平方)。
4. 邻接矩阵的优缺点
优点
- 快速判断两顶点是否相邻:直接访问
arc[i][j]。 - 方便计算顶点的度:
无向图:第 i i i 行非INF的元素个数。
有向图:第 i i i 行的和是出度,第 i i i 列的和是入度。
缺点
- 空间浪费:存储稀疏图时存在大量无效元素。
- 添加/删除顶点成本高:需要调整二维数组大小。
5. 代码运行示例
输入数据
顶点数:4
边数:4
顶点名称:A B C D
边信息:
0 1 5
1 2 3
1 3 2
-1 -1
输出结果
顶点表: A B C D
邻接矩阵:∞ 5 ∞ ∞5 ∞ 3 2∞ 3 ∞ ∞∞ 2 ∞ ∞
这里是用mermaid语法,应该有个箭头的
2.2 邻接表
1.邻接表的定义
当一个图为稀疏图时(边数相对顶点较少),使用邻接矩阵法显然要浪费大量的存储空间,而图的邻接表法结合了顺序存储和链式存储方法,大大减少了这种不必要的浪费。
邻接表(Adjacency List) 是图的链式存储结构,通过为每个顶点维护一个链表来存储其邻接顶点信息。
- 核心思想:仅存储实际存在的边,避免稀疏图中的空间浪费。
- 适用场景:稀疏图(边数 e e e 远小于顶点数 n n n 的平方)。
2. 存储结构组成
邻接表由 顶点表 和 边表(邻接表) 两部分组成:
顶点表(头结点)
用一个数组(或结构体数组)存储图中所有顶点的信息,每个顶点包含两部分:
顶点自身的数据(如编号、名称等);
一个指针,指向该顶点对应的边表(即所有与该顶点相邻的边 / 弧)。
边表(边结点)
每个顶点对应一个 单链表(边表),链表中的每个节点(边节点)表示与该顶点相邻的一条边(或弧),包含以下信息:
邻接顶点的编号(即边的另一端顶点在顶点表中的位置);
边的权值(若为带权图,需额外存储权值;无权图可省略);
指向下一个邻接边节点的指针,用于连接同一顶点的所有邻接边。

无向图示例

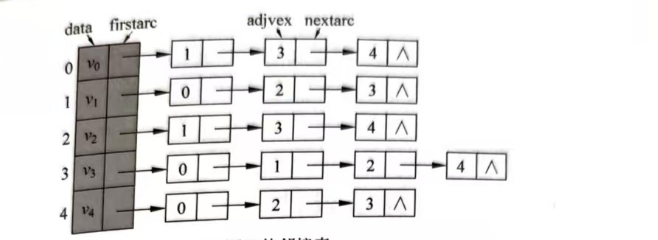
有向图示例


代码表示
(1)头文件和声明
#include<iostream>
#include<math.h>
#include<stdio.h>#define MAXV 20
#define INF 1e9
typedef int InfoType;
typedef struct ANode
{int adjvex; //该边的邻接点的编号struct ANode* nextarc; //指向下一边的指针int weight; //该边的相关信息(这里是整形的权值)
}ArcNode; //边结点的类型typedef struct Vnode
{InfoType data; //顶点的其他信息ArcNode* firstarc;//指向第一个边结点
}VNode; //邻接表头结点的类型typedef struct
{VNode adjlist[MAXV];//邻接表头结点的数组int n; //顶点数int e; //边数
}AdjGraph; //完整图的类型(2) 创建图
以单向有向图为例
//创建图
void CreateAdj(AdjGraph*& G, int A[MAXV][MAXV], int n, int e) {int i, j;ArcNode* p; // 临时边结点指针// 1. 分配图的内存空间G = (AdjGraph*)malloc(sizeof(AdjGraph));if (G == NULL) { /* 错误处理,此处省略 */ }// 2. 初始化顶点结点:清空每个顶点的邻接表(表头指针置空)for (i = 0; i < n; i++) {G->adjlist[i].firstarc = NULL; // 顶点i的邻接表初始化为空G->adjlist[i].data = 0; // 顶点数据(若有需要可自定义初始化)}// 3. 遍历邻接矩阵,构建邻接表(头插法)for (i = 0; i < n; i++) { // 遍历每个顶点(作为起点)for (j = n - 1; j >= 0; j--) { // 从后往前遍历列(头插法,保证邻接顺序与矩阵行顺序一致)if (A[i][j] != 0 && A[i][j] != INF) { // 非自环边且存在有效边// 创建新边结点:表示顶点i到j的边p = (ArcNode*)malloc(sizeof(ArcNode));p->adjvex = j; // 目标顶点为jp->weight = A[i][j]; // 边权赋值// 头插法:将新边插入到顶点i邻接表的头部p->nextarc = G->adjlist[i].firstarc; // 新边的下一条边为原表头边G->adjlist[i].firstarc = p; // 表头更新为新边}}}// 4. 设置图的顶点数和边数(用于后续操作)G->n = n;G->e = e;
}
(3)输出图
//输出
void DisAdj(AdjGraph* G) {int i; // 顶点索引ArcNode* p; // 遍历邻接表的临时指针for (i = 0; i < G->n; i++) { // 遍历每个顶点p = G->adjlist[i].firstarc; // 获取顶点i的邻接表表头printf("%3d:", i); // 输出顶点编号// 遍历邻接表,输出所有邻接边while (p != NULL) {// 输出格式:邻接顶点编号[边权]->printf("%3d[%d]->", p->adjvex, p->weight);p = p->nextarc; // 移动到下一条邻接边}printf("^\n"); // 邻接表结束标志(^表示链表终止)}
}
(3)销毁图
void DeatroyAdj(AdjGraph* G) {int i; // 顶点索引ArcNode *pre, *p; // 双指针法释放链表内存:pre指向当前结点,p指向下一结点for (i = 0; i < G->n; i++) { // 遍历每个顶点的邻接表pre = G->adjlist[i].firstarc; // 获取邻接表表头if (pre == NULL) continue; // 若邻接表为空,跳过p = pre->nextarc; // p初始化为第一个结点的下一个结点while (p != NULL) { // 循环直到链表末尾free(pre); // 释放当前结点内存pre = p; // pre后移到p的位置p = p->nextarc;// p后移到下一个结点}free(pre); // 释放最后一个结点(循环结束后pre指向最后一个结点)G->adjlist[i].firstarc = NULL; // 清空表头指针(}free(G); // 释放图的整体内存G = NULL; // 置空指针
}
3. 无向图与有向图的存储方式
| 图类型 | 存储规则 | 空间复杂度 |
|---|---|---|
| 无向图 | 每条边 ( v i , v j ) (v_i, v_j) (vi,vj) 存储两次: - 在 v i v_i vi 的邻接链表中插入 v j v_j vj - 在 v j v_j vj 的邻接链表中插入 v i v_i vi | O ( n + 2 e ) O(n + 2e) O(n+2e) → 简化为 O ( n + e ) O(n + e) O(n+e) |
| 有向图 | 每条弧 ⟨ v i , v j ⟩ \langle v_i, v_j \rangle ⟨vi,vj⟩ 存储一次: - 仅在 v i v_i vi 的邻接链表中插入 v j v_j vj | O ( n + e ) O(n + e) O(n+e) |
4. 顶点度的计算
-
无向图:
- 顶点的度 = 邻接链表的节点数。
- 总边数 e = 1 2 ∑ i = 0 n − 1 链表长度 ( i ) e = \frac{1}{2} \sum_{i=0}^{n-1} \text{链表长度}(i) e=21∑i=0n−1链表长度(i)
-
有向图:
- 出度 = 邻接链表的节点数。
- 入度:需遍历所有邻接链表,统计目标顶点出现的次数(或使用逆邻接表优化)。
5. 优缺点对比
优点
- 空间高效:仅存储实际存在的边,适合稀疏图。
- 动态扩展灵活:添加/删除边只需操作链表。
- 便于遍历邻接顶点:直接访问链表即可。
缺点
- 判断边存在性慢:需遍历链表,最坏情况 O ( e ) O(e) O(e)。
- 计算入度复杂:需遍历全表(可结合逆邻接表优化)。
总结
由于内容过多(写的有点冗余),度的计算,DFS、BFS将在另一篇文章更新,如有错误还望指正,也请多多三连支持一下,谢谢
