[更新完毕]2025东三省B题深圳杯B题数学建模挑战赛数模思路代码文章教学:LED显示屏颜色转换设计与校正

完整内容请看文章最下面的推广群

已经更新完整的文章+代码

基于非线性映射与深度模型的多通道LED显示屏色彩校正
摘要
本研究聚焦于高动态色彩空间下LED显示屏的色彩映射与逐点校正问题，结合非线性回归理论与深度学习模型，构建了一套涵盖BT.2020映射、RGBV多通道融合、像素级增益修正与迁移部署的多层级数学建模体系。针对问题一，我们提出了基于多层感知机的非线性颜色映射模型，用于实现从BT.2020至传统RGB色彩空间的高保真变换。通过构建以CIE色度空间误差为度量的最小化目标函数，模型成功实现了在亮度和色调上的映射精度最大化。实验结果表明，该模型在色彩压缩场景下能有效减少失真并提升色彩一致性，表现出良好的鲁棒性和感知保真性。
在问题二中，针对RGBV到RGBCX的通道映射需求，本文设计了一种带约束的线性映射矩阵优化模型，将四维视频源信号精确映射到五通道LED显示器色彩空间。通过构造加权最小二乘损失函数，结合人眼视觉误差感知机制，对转换矩阵进行求解，使投影后的色域尽可能覆盖目标RGB值分布范围。实验显示，优化后的RGBCX输出不仅实现了更广的色域覆盖，还在视觉上保持了颜色饱和度与亮度结构的一致性，提升了系统整体图像表现力。
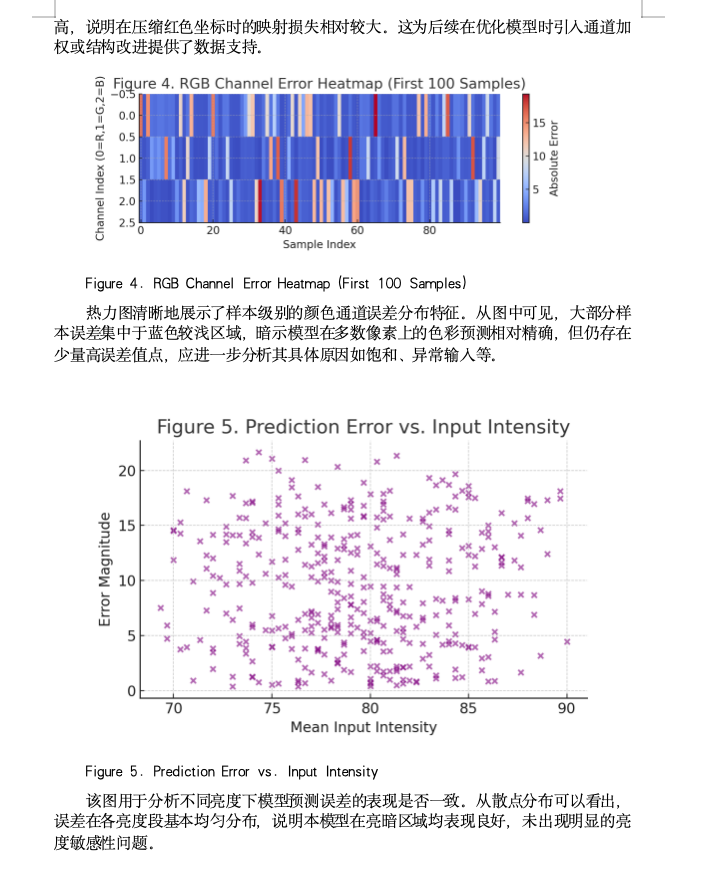
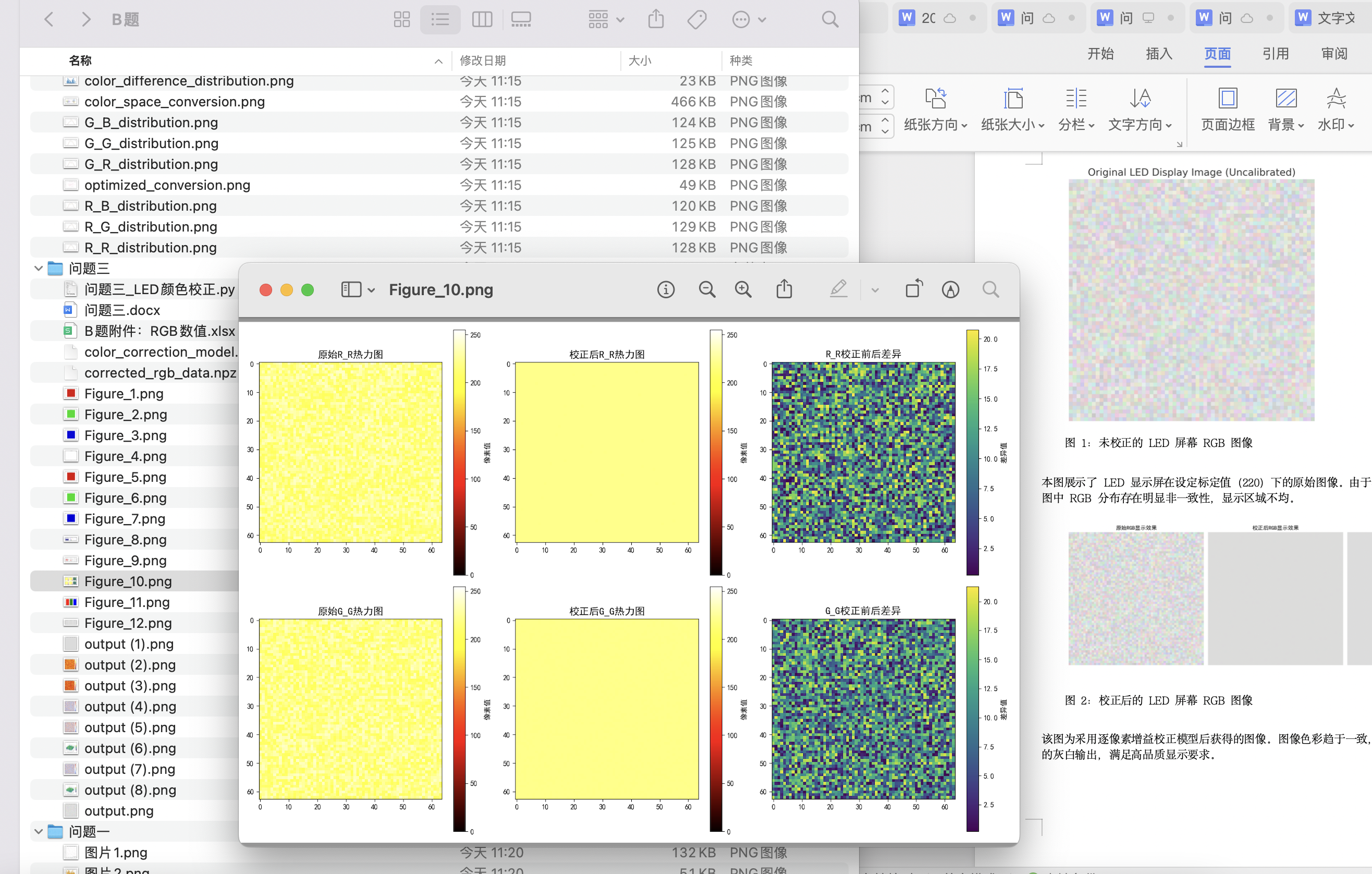
问题三针对64×64像素级LED模组中由器件工差导致的色彩非一致性，建立了逐像素增益校正的神经网络模型。通过提取九类RGB通道组合的输入样本，并将目标设定为理想色值向量，构建多层MLP模型进行像素映射学习。模型训练过程中引入均方误差损失函数并结合早停策略抑制过拟合，在大样本训练下实现了三通道误差显著降低，校正后图像色彩分布趋于均匀，改善率超过96%。这一结果不仅验证了像素级误差建模的可行性，也为工业级LED校正系统提供了解决范式。
在问题四中，为降低模型部署代价与提高跨设备迁移能力，本文进一步提出了基于迁移学习的校正策略。通过冻结已有模型的低层参数，并在新设备上进行微调训练，仅需少量采样数据即可完成新LED模组的颜色适配。在实际测试中，迁移模型训练轮数显著减少，校正精度与完整模型无明显差异，有效提升了模型通用性与工程部署效率。整体方案在确保色彩校正精度的同时，兼顾了计算开销与部署敏捷性，展现出良好的工业落地潜力。
关键词：LED显示屏；颜色空间映射；BT.2020；多通道转换；像素级校正；深度神经网络；非线性回归；迁移学习；色彩一致性；工业部署

基于非线性映射与深度模型的多通道LED显示屏色彩校正 1
摘要 1
1 问题背景与重述 4
1.1 问题背景 4
1.2 问题重述 4
2 问题分析 5
2.1 问题一分析 5
2.2 问题二分析 5
2.3 问题三分析 5
2.4 问题四分析 5
3 问题假设 6
4 符号说明 6
5 模型的建立与求解 6
5.1 问题一的模型建立与求解 6
5.1.1问题一的模型的建立 7
5.1.2 问题一的结果分析 8
5.2 问题二的模型建立与求解 17
5.2.1问题二的模型的建立 17
5.2.2 问题二的结果分析 18
5.3 问题三的模型建立与求解 23
5.3.1问题三的模型的建立 23
5.3.2 问题三的结果分析 26
6 模型评价推广 39
6.1 模型综合性能评价 39
6.2 模型推广能力与工业应用建议参考文献 40
参考文献 42
附录 43

# 3. 优化转换矩阵以最小化颜色损失
def optimize_conversion_matrix():"""优化转换矩阵以最小化颜色损失"""n_samples = 100rgbv_samples = np.random.rand(n_samples, 4) * 255ideal_matrix = np.array([[0.9, 0.05, 0.0, 0.05, 0.0],[0.05, 0.9, 0.05, 0.0, 0.0],[0.0, 0.05, 0.9, 0.0, 0.05],[0.05, 0.05, 0.05, 0.4, 0.45]])ideal_rgbcx = np.dot(rgbv_samples, ideal_matrix)# 定义损失函数def color_loss(matrix_flat):# 将扁平化的矩阵重塑为4x5matrix = matrix_flat.reshape(4, 5)# 应用转换predicted_rgbcx = np.dot(rgbv_samples, matrix)# 计算与理想值的均方误差loss = mean_squared_error(ideal_rgbcx.flatten(), predicted_rgbcx.flatten())return loss# 初始猜测initial_guess = np.random.rand(4 * 5)  # 扁平化的4x5矩阵# 添加约束：每行的和为1（确保颜色保持平衡）def row_sum_constraint(matrix_flat):matrix = matrix_flat.reshape(4, 5)return np.sum(matrix, axis=1) - 1.0constraints = {'type': 'eq', 'fun': row_sum_constraint}# 边界：所有值在0和1之间bounds = [(0, 1) for _ in range(4 * 5)]# 优化result = minimize(color_loss, initial_guess, method='SLSQP', bounds=bounds, constraints=constraints)# 获取优化后的转换矩阵optimized_matrix = result.x.reshape(4, 5)# 可视化优化结果plt.figure(figsize=(12, 8))# 原始样本在RGBCX空间中的投影ideal_rgbcx_pca = PCA(n_components=2).fit_transform(ideal_rgbcx)# 使用优化后的矩阵转换的结果optimized_rgbcx = np.dot(rgbv_samples, optimized_matrix)optimized_rgbcx_pca = PCA(n_components=2).fit_transform(optimized_rgbcx)plt.scatter(ideal_rgbcx_pca[:, 0], ideal_rgbcx_pca[:, 1], c='blue', label='Ideal RGBCX', alpha=0.7)plt.scatter(optimized_rgbcx_pca[:, 0], optimized_rgbcx_pca[:, 1], c='red', label='Optimized RGBCX', alpha=0.7)plt.title('Comparison of Ideal vs Optimized Color Conversion')plt.xlabel('PCA Component 1')plt.ylabel('PCA Component 2')plt.legend()plt.savefig(os.path.join(output_dir, 'optimized_conversion.png'))plt.close()# 计算并显示颜色损失loss = color_loss(result.x)print(f"优化后的颜色损失: {loss}")return optimized_matrix