Top100(26-30)
二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
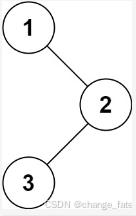
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
解法一: 递归
function inorderTraversal(root: TreeNode | null): number[] {const resArr: number[] = []if (root == null) return resArr inOrder(root, resArr)return resArr
};
function inOrder(node: TreeNode, resArr: number[]) {if (node == null) returninOrder(node.left, resArr)resArr.push(node.val)inOrder(node.right, resArr)
};
解法二:非递归
- 思路:
- (1)准备辅助栈,当二叉树节点为空了且栈中没有节点了,我们就停止访问。
- (2)从根节点开始,每次优先进入每棵的子树的最左边一个节点,我们将其不断加入栈中,用来保存父问题。
- (3)到达最左后,可以开始访问,如果它还有右节点,则将右边也加入栈中,之后右子树的访问也是优先到最左。
var inorderTraversal = function (root) {let stack = []let res = []let cur = rootconsole.log(root)while (cur != null || stack.length > 0) {if (cur != null) {stack.push(cur)cur = cur.left} else {cur = stack.pop()res.push(cur.val)cur = cur.right}}return res
二叉树的最大深度
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
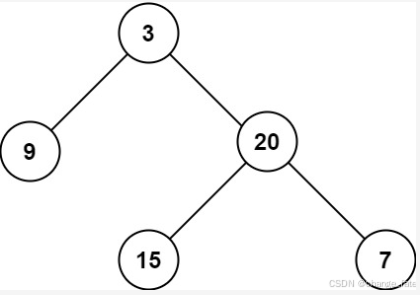
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
解法一: 递归
思路:
(1)最大深度是所有叶子节点的深度的最大值,深度是指树的根节点到任一-叶子节点路径上节点的数量,
(2)因此从根节点每次往下一层深度就会加1。
(3)因此二叉树的深度就等于根结点这个1层加上左子树和右子树深度的最大值
时间复杂度: O(n),其中n为二叉树的节点数,遍历整棵二叉树
空间复杂度: O(n),最坏情况下,二叉树化为链表,递归栈深度最大为n
function maxDepth(root: TreeNode | null): number {if (root == null) return 0return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
};
解法二: 层遍历
var maxDepth = function (root) {if (root == null) { return 0 }let q = [root]let depth = 0while (q.length !== 0) {let sz = q.lengthfor (let i = 0; i < sz; i++) {let cur = q.shift()if (cur.left) {q.push(cur.left)}if (cur.right) {q.push(cur.right)}}depth++}return depth
岛屿最大面积【Medium】
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
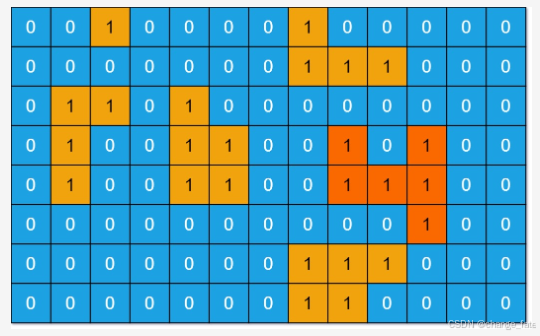
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
TODO:
LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
TODO: 不想看
零钱兑换
TODO: 动态规划
链表中倒数第K个节点
TODO没找到
斐波那契数 【easy】
解法1: 递归法
var fib = function (n) {if (n < 2) {return n}return fib(n - 2) + fib(n - 1)
};
解法二: 迭代法
var fib = function (n) {if (n < 2) {return n}let a1 = 0let a2 = 1let res = 0for (let i = 1; i < n; i++) {res = a1 + a2a1 = a2a2 = res}return res
}
翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
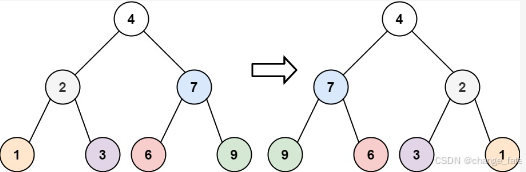
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
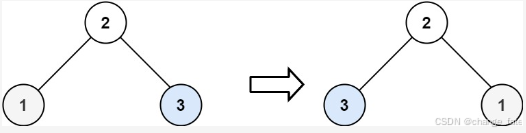
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
解法一: 递归
var invertTree = function (root) {traverse(root);return root;
};function traverse(root) {if (root == null) {return}let tmp = root.leftroot.left = root.rightroot.right = tmpinvertTree(root.left)invertTree(root.right)
}
解法二:
var invertTree = function (root) {
// 方法二:
if (root == null) {
return null
}
let left = invertTree(root.left)
let right = invertTree(root.right)
root.left = right
root.right = left
return root
};
长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
解法一:暴力法
解法二: 滑动窗口
var minSubArrayLen = function (target, nums) {let left = 0let right = 0let sum = 0let result = Infinitylet subLength = nums.lengthwhile (right < subLength) {sum += nums[right]while (sum >= target) {result = Math.min(result, right - left + 1)sum -= nums[left++]}right++}return result === Infinity ? 0 : result
};
接雨水
TODO 动态规划
最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
TODO: 动态规划
二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
解法一:递归
var preorderTraversal = function (root) {if (root == null) {return []}let res = []function traversal(node) {if (!node) returnres.push(node.val)traversal(node.left)traversal(node.right)}traversal(root)return res
};
合并区间 【Medium】
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
思路:
首先对输入的区间数组进行排序,然后通过一个循环和条件判断来合并重叠的区间。如果合并后的数组为空或者当前区间不与合并后数组的最后一个区间重叠,就将其直接添加到结果中。如果重叠,则更新合并后数组的最后一个区间的右端点。最终返回合并后的区间数组。
TODO
二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:
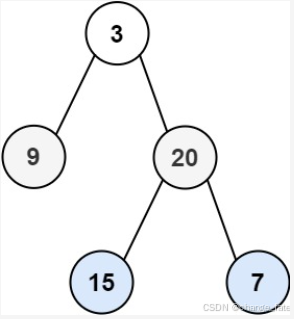
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
