当前位置：首页 > web >正文

无向图的连通性问题

web 2025/7/28 13:08:07

前置知识点:图的DFS 树，DFS 序

无向图的连通分量

连通分量是指一个无向图的一个极大连通子图，连通分量中的任意两个点都存在一条路径可以直接或间接互相到达。

对于一个无向图，如何求出它的所有连通分量呢？

算法一：图上 DFS

对于一个没有访问过的点，我们从这个点开始DFS，访问所有还没有访问过的点，每访问到一个点，我们就将其标记为已访问。在某一个点 DFS 结束时，所有在这一轮访问到的点就在一个连通分量中。显然该算法的时间复杂度为 O(n+m)O(n+m) 。

参考代码：

const int N = 1e5+5;
int n, m;
int fa[N], vis[N], root;  // fa[i]: 节点 i 所在连通分量的代表元素
int vector<int> g[N];
void dfs(int u) {vis[u] = 1;fa[u] = root;for(auto v : g[u]) {if(!vis[v])dfs(v);}
}for(int i = 1; i <= n; i++) {if(!vis[i]) {root = i;dfs(i);}
}

算法二：并查集

通过扫描所有的边，不断合并两个连通分量，最终形成图的各个连通分量。算法时间复杂度为： O(n+mα(n))O(n+mα(n)) 。

参考代码：

const int N = 1e5+5;
int n, m;
int fa[N];
int find(int x) {if(fa[x] == x) return x;return fa[x] = find(fa[x]);
}
void  merge(int x, int y) {x = find(x);y = find(y);fa[x] = y;
}
int main() {cin >> n >> m;for(int i = 1; i <= n; i++) fa[i] = i;for(int i = 1; i <= m; i++) {int u, v;cin >> u >> v;merge(u, v);}
}

❓问题： 在对图进行遍历后，能否快速判断某个连通分支是一棵树？

🚩回答： 如果使用 DFS 遍历来实现，那么只要在扩展时，走到走过的节点，就说明存在“冗余的边”，不可能是树。如果使用并查集，那么在合并时如果两个节点的祖先相同，则说明存在“冗余的边”，不可能是树。

练习题

P4786 无向图的连通分量 - TopsCoding
P1203 细胞 - TopsCoding

无向图的割点和桥

前置概念（定义）

点连通度 ：在一个无向连通图中，如果有一个顶点集合 VV ，删除顶点集合 VV 以及与 VV 中顶点相连（至少有一端在 VV 中）的所有边后，原图不连通，就称这个点集 VV 为 割点集合 。大小为 11 的点割集又被称作割点。

一个图的点连通度 ：最小割点集合中的顶点数。

边连通度 ：在一个无向连通图中，如果有一个边集合 EE ，删除这个边集 EE 中的边以后，原图不连通，就称这个边集 EE 为 割边集合 。

一个图的边连通度 ：最小割边集合中的边数。大小为 11 的边割集又被称作桥。

点双连通图 ：如果一个无向连通图的点连通度大于 11 ，则称该图是点双连通的（point biconnected），简称点双连通或点重连通(即删去任意一点原图仍然连通)。换句话说， 没有割点的连通图是点双连通的 。

边双连通图 ：如果一个无向连通图的边连通度大于 11 ，则称该图是边双连通的（edge biconnected），简称边双连通或边重连通(即删去任意一条边原图仍然连通)。换句话说， 没有桥的连通图是边双连通的 。

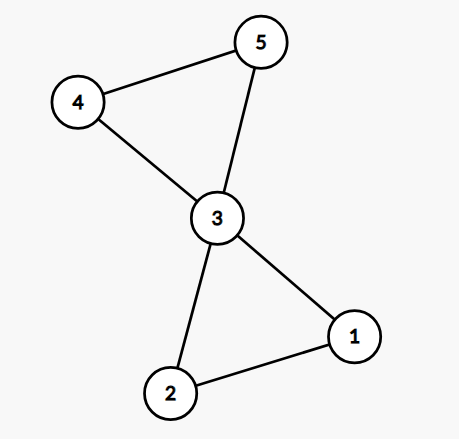
割点：一个图有割点，当且仅当这个图的点连通度为 11 时，割点集合的唯一元素被称为割点(cut point)(即删去割点原图不连通)。一个图可能有多个割点。有割点的图不一定有割边，如下图所示，结点 33 为割点，但是图中没有割边。

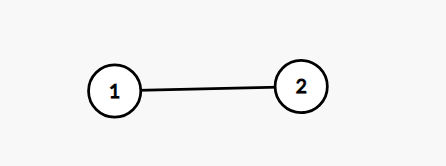
割边（桥） ：如果一个无向连通图的边连通度大于 11 ，则称该图是边双连通的(edge biconnected)，简称双连通或重连通(即删去任意一边原图仍然连通)。一个图有桥，当且仅当这个图的边连通度为 11 时，割边集合的唯一元素被称为桥(bridge)(即删去桥原图不连通)。一个图可能有多个桥。有割边的图也不一定有割点，如下图所示。

根据定义做两个猜想：两个割点之间的边一定是割边。割边的两个端点一定是割点。

可惜的是，这两个猜想都是错误的！反例如下图：

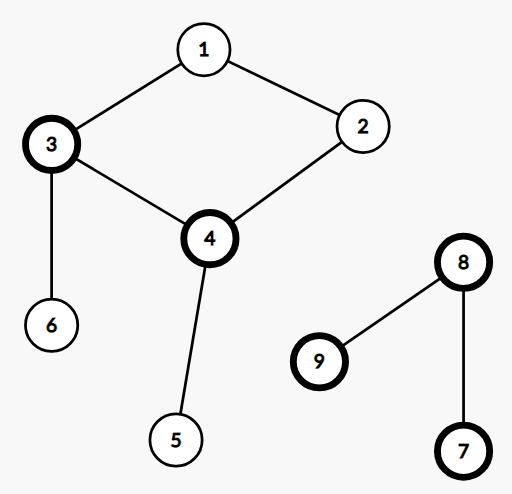
上图中，结点 3,43,4 为割点，但是边 (3,4)(3,4) 不是割边。边 (7,8),(8,9)(7,8),(8,9) 为割边，但点 7,97,9 不是割点。

通俗版定义

对于一个无向图，如果把一个点删除后这个图的连通块（极大连通分量）数增加了，那么这个点就是这个图的割点（又称割顶）。

Tarjan 求无向图的割点和桥

根据著名计算机科学家 Robert Tarjan 的名字命名的 Tarjan 算法能够在线性时间内求出无向图的割点与桥，进一步可求出无向图的双连通分量。在有向图方面，Tarjan 算法能够求出有向图的强连通分量、必经点与必经边(下一节将会介绍)。Robert Tarjan 在数据结构方面也做出了很多卓有成效的工作，包括证明并查集的时间复杂度，提出斐波那契堆、Splay Tree 和 Lint-Cut Tree 等。

1. 时间戳

在图的 深度优先遍历 过程中，按照每个节点第一次被访问的时间顺序，依次给予 NN 个节点 1∼N1∼N 的整数标记，该标记就被称为“时间戳”，记为 dfn[x]dfn[x] 。

2. 搜索树

在无向连通图中任选一个节点出发进行深度优先遍历,每个点只访问一次。所有发生递归的边 (x,y)(x,y) （换言之，从 xx 到 yy 是对 yy 的第一次访问）构成一棵树，我们把它称为“无向连通图的搜索树”。当然，一般无向图（不定连通）的各个连通块的搜索树构成无向图的“搜索森林”。

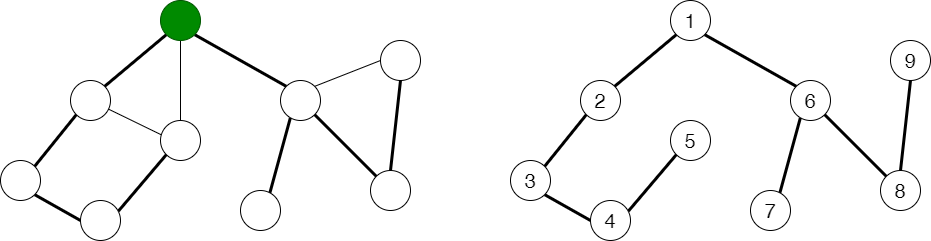
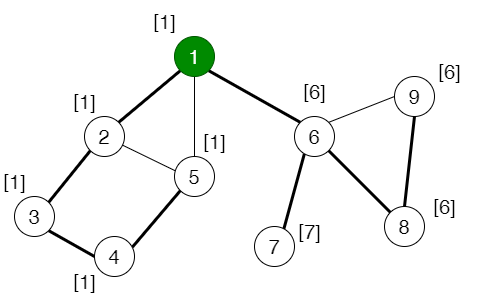
下图左侧展示了一张无向连通图，绿色节点是深度优先遍历的起点，加粗的边是“发生递归”的边（假设我们在遇到多个分支时，总是优先访问最靠左的一条)。右侧展示了深度优先遍历的搜索树，并标注了节点的时间戳。

graph

3. 追溯值

除了时间戳之外，Tarjan 算法还引入了一个“追溯值” low[x]low[x] 。设 subtree(x)subtree(x) 表示搜索树中以 xx 为根的子树。 low[x]low[x] 定义为以下节点的时间戳的最小值：

subtree(x)subtree(x) 中的节点。
通过一条不在搜索树上的边，能够到达 subtree(x)subtree(x) 的节点。

简而言之， xx 的追溯值 low[x]low[x] 定义为 xx 或 xx 的子树能够回溯到的最早的栈中节点的 dfndfn 值 。

以上图为例。为了叙述简便，我们用时间戳代替节点编号。 subtree(2)={2,3,4,5}subtree(2)={2,3,4,5} 。另外，节点 11 通过不在搜索树上的边 (1,5)(1,5) 能够到达 subtree(2)subtree(2) 。所以 low[2]=1low[2]=1 。

根据定义，为了计算 low[x]low[x] ，应该先令 low[x]=dfn[x]low[x]=dfn[x] ，然后考虑从 xx 出发的每条边 (x,y)(x,y) ：

若在搜索树上 xx 是 yy 的父节点，则令 low[x]=min⁡(low[x],low[y])low[x]=min(low[x],low[y]) 。
若无向边 (x,y)(x,y) 不是搜索树上的边，则令 low[x]=min⁡(low[x],dfn[y])low[x]=min(low[x],dfn[y]) 。下图的中括号里的数值标注了每个节点的“追溯值” lowlow 。

割边判定法则

无向边 (x,y)(x,y) 是桥，当且仅当搜索树上存在 xx 的一个子节点 yy ，满足：

dfn[x]<low[y]dfn[x]<low[y]

根据定义， dfn[x]<low[y]dfn[x]<low[y] 说明从 subtree(y)subtree(y) 出发在不经过 (x,y)(x,y) 的前提下，不管走哪条边，都无法到达 xx 或比 xx 更早访问的节点。若把 (x,y)(x,y) 删除，则 subtree(y)subtree(y) 就好像形成了一个封闭的环境，与节点 xx 没有边相连，图断开成了两部分。因此 (x,y)(x,y) 是割边。

反之，若不存在这样的子节点 yy ，使得 dfn[x]<low[y]dfn[x]<low[y] ，则说明每个 subtree(y)subtree(y) 都能绕行其他边到达 xx 或比 xx 更早访问的节点， (x,y)(x,y) 自然就不是割边。

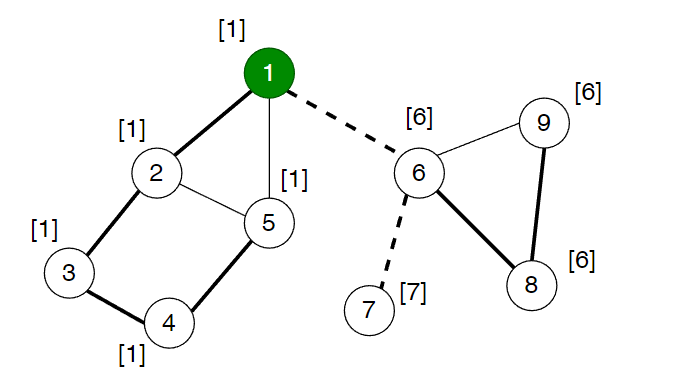
下面的无向图中有两条“桥”边，用虚线标识。读者不难发现，桥一定是搜索树中的边，并且一个简单环中的边一定都不是桥。

下面的程序求出一张无向图中所有的桥。特别需要注意，因为我们遍历的是无向图，所以从每个点 xx 出发，总能访问到它的父节点 fafa 。根据 low[]low[] 的计算方法， (x,fa)(x,fa) 属于搜索树上的边(无向边=两条双向边)，且 fafa 不是 xx 的子节点故不能用 fafa 的时间来更新 low[x]low[x] 。

但是， 如果仅记录每个节点的父节点，会无法处理重边的情况——当 xx 与 fafa 之间有多条边时， (x,fa)(x,fa) 一定不是桥 。在这些重复的边中，只有一条算是“搜索树上的边”，其他的几条都不算。故有重边时， dfn[fa]dfn[fa] 能用来更新 low[x]low[x] 。

一个好的解决方案是：改为记录“递归进入每个节点的边的编号”。编号可认为是边在邻接表中存储的下标位置。我们可以用“成对变换”技巧（ 使用链式前向星存边 ）。把无向图的每条边看作双向边，成对存储在下标“2和3”、“4和5”、“6和7”、......处。若沿着编号为 ii 的边递归进入了节点 xx ，则忽略从 xx 出发的编号为 i xor 1i xor 1 的边，通过其他边计算 low[x]low[x] 即可。

模板题：P6811 无向图的割边（桥） - TopsCoding

参考代码：

#include <bits/stdc++.h>
using namespace std;const int N = 1e5+5;
int head[N], ver[N*2], Next[N*2];
int dfn[N], low[N], n, m, tot = 1, num;
bool bridge[N*2];void add(int x, int y) {ver[++tot] = y;Next[tot] = head[x];head[x] = tot;
}void tarjan(int x, int in_edge) {dfn[x] = low[x] = ++num;for(int i = head[x]; i; i = Next[i]) {int y = ver[i];if(!dfn[y]) {tarjan(y, i);low[x] = min(low[x], low[y]);if(low[y] > dfn[x]) { // 是割边（桥）bridge[i] = bridge[i^1] = true;}} // 否则，不是搜索树边，且不是同一条边else if(i != (in_edge^1)) {low[x] = min(low[x], dfn[y]);}}
}int main(){cin >> n >> m;while(m--) {int x, y;cin >> x >> y;add(x, y); add(y, x);  // 这里同一条边是相邻存进“链式前向星”里的,一奇一偶}for(int i = 1; i <= n; i++) {if(!dfn[i]) tarjan(i, 0);}vector<pair<int, int> > ans;for(int i = 2; i <= tot; i+=2) {if(bridge[i]) {int x = ver[i^1], y = ver[i];if(x > y) swap(x, y);ans.push_back(make_pair(x, y));}}cout << ans.size() << '\n';sort(ans.begin(), ans.end());for(auto p : ans)cout << p.first << ' ' << p.second << '\n';return 0;
}

割点判定法则

若 xx 不是搜索树的根节点(深度优先遍历的起点)，则 xx 是割点当且仅当搜索树上存在 xx 的一个子节点 yy ，满足：

dfn[x]≤low[y]dfn[x]≤low[y]

特别地，若 xx 是搜索树的根节点，则 xx 是割点当且仅当搜索树上存在至少两个子节点 y1,y2y1,y2 满足上述条件。这是因为如果只有一棵子树,去掉根结点后肯定不会出现多棵子树，因此就不会是割点。

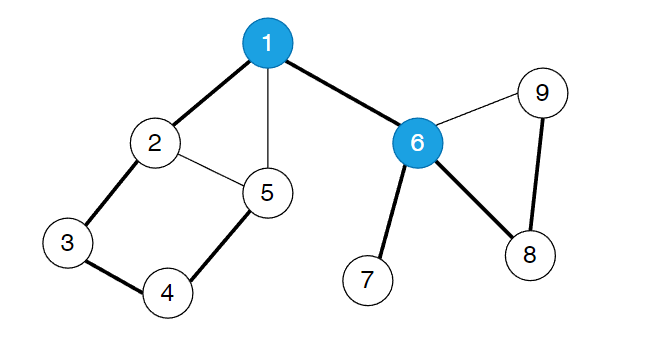
证明方法与割边的情形类似，这里就不再赘述(删去 xx 后 yy 及它的子树上的结点就不能到达 xx 的祖先)。在“割边判定法则”画出的例子中，共有2个割点，分别是时间戳为 11 和 66 的两个点。

下面的程序求出一张无向图中所有的割点。因为割点判定法则是小于等于号，所以在求割点时，不必考虑父节点和重边的问题，从 xx 出发能访问到的所有点的时间戳都可以用来更新 low[x]low[x] 。

模板题: P6812 无向图的割点（割顶） - TopsCoding

参考代码:

#include <bits/stdc++.h>
using namespace std;const int N = 1e5+5;
int head[N], ver[N*2], Next[N*2];
int dfn[N], low[N], n, m, tot = 1, num, root, ans;
bool cut[N];void add(int x, int y) {ver[++tot] = y;Next[tot] = head[x];head[x] = tot;
}void tarjan(int x) {dfn[x] = low[x] = ++num;int flag = 0;for(int i = head[x]; i; i = Next[i]) {int y = ver[i];if(!dfn[y]) {tarjan(y);low[x] = min(low[x], low[y]);if(low[y] >= dfn[x]) {flag++;if(x != root || flag > 1) cut[x] = true;}} // 否则，不是搜索树边else  {low[x] = min(low[x], dfn[y]);}}
}int main(){cin >> n >> m;while(m--) {int x, y;cin >> x >> y;if(x == y) continue;add(x, y); add(y, x);  // 这里同一条边是相邻存进“链式前向星”里的}for(int i = 1; i <= n; i++) {if(!dfn[i]){root = i;tarjan(i);}}for(int i = 1; i <= n; i++) {if(cut[i]) ans++;}cout << ans << '\n';for(int i = 1; i <= n; i++)if(cut[i]) cout << i << ' ';return 0;
}

练习题

P6811 无向图的割边（桥） - TopsCoding
P6812 无向图的割点（割顶） - TopsCoding
P4787 POI 2008 城市封锁 - TopsCoding

无向图的双连通分量

定义

在一张连通的无向图中，对于两个点 uu 和 vv ，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 uu 和 vv 边双连通 。

在一张连通的无向图中，对于两个点 uu 和 vv ，如果无论删去哪个点（只能删去一个，且不能删 uu 和 vv 自己）都不能使它们不连通，我们就说 uu 和 vv 点双连通 。

边双连通具有传递性，即，若 x,yx,y 边双连通， y,zy,z 边双连通，则 x,zx,z 边双连通。

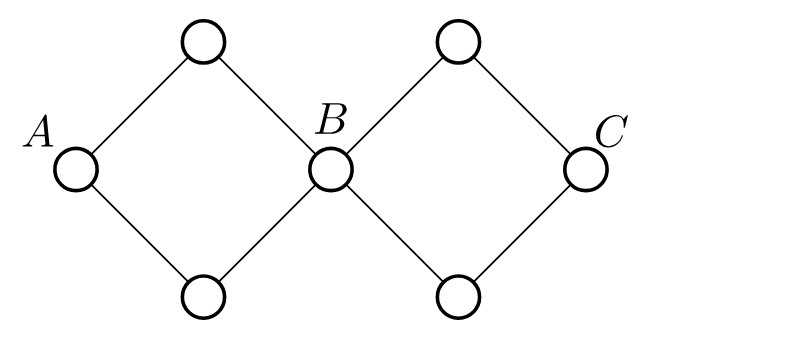
点双连通不具有传递性，反例如下图， A,BA,B 点双连通， B,CB,C 点双连通，而 A,CA,C 不点双连通。

若一张无向连通图不存在割点，则称它为“点双连通图”。若一张无向连通图不存在桥，则称它为“边双连通图”。

无向图的极大点双连通子图被称为“点双连通分量”，简记为“v-DCC”(vertex double connected component)。无向连通图的极大边双连通子图被称为“边双连通分量”，简记为“e-DCC”(edge double connected component)。二者统称为“双连通分量”，简记为“DCC”。

在上面的定义中，我们称一个双连通子图 G′=(V′,E′)G′=(V′,E′) “极大”(其中 V′⊆VV′⊆V ， E′⊆EE′⊆E )，是指不存在包含 G′G′ 的更大的子图 G′′=(V′′,E′′)G′′=(V′′,E′′) ，满足 V′⊆V′′⊆VV′⊆V′′⊆V ， E′⊆E′′⊆EE′⊆E′′⊆E 并且 G′′G′′ 也是双连通子图。

定理

一张无向连通图是“点双连通图” ，当且仅当满足下列两个条件之一：

图的顶点数不超过 22 。
图中任意两点都同时包含在至少一个简单环中。其中“简单环”指的是不自交的环，也就是我们通常画出的环。

一张无向连通图是“边双连通图” ，当且仅当任意一条边都包含在至少一个简单环中。

证明：

该定理给出了无向连通图是“点双连通图”或“边双连通图”的充要条件。我们以“点双连通图”为例进行证明，对于“边双连通图”的证明，请尝试自己完成证明。

对于顶点数不超过 22 的情况，定理显然成立，下面假设图中顶点数不小于 33 。

先证 充分性 。若任意两点 x,yx,y 都同时包含在至少一个简单环中，则 x,yx,y 之间至少有两条不相交的路径。无论从图中删除哪个节点， x,yx,y 均能通过两条路径之一相连。故图中不存在割点，是点双连通图。

再证 必要性 。反证法，假设一张无向连通图是“点双连通图”，并且存在两点 x,yx,y 它们不同时处于任何一个简单环中。如果 x,yx,y 之间仅存在 11 条简单路径，那么路径上至少有一个割点，与“点双连通”矛盾。

如果 x,yx,y 之间存在 22 条或 22 条以上的简单路径，那容易发现，任意两条都至少有一个除 x,yx,y 之外的交点；进一步可推导出， x,yx,y 之间的所有路径必定同时交于除 x,yx,y 之外的某一点 pp (不然就会存在两条没有交点的路径，形成一个简单环)。根据定义， pp 是一个点，这与“点双连通”矛盾。故假设不成立。

证毕。

e-DCC 的求法

边双连通分量(e-DCC)的求法边双连通分量的计算非常容易。只需求出无向图中所有的桥，把桥都删除后，无向图会分成若干个连通块，每一个连通块就是一个“边双连通分量”下面的无向图共有 22 条“桥”边， 33 个“边双连通分量”：

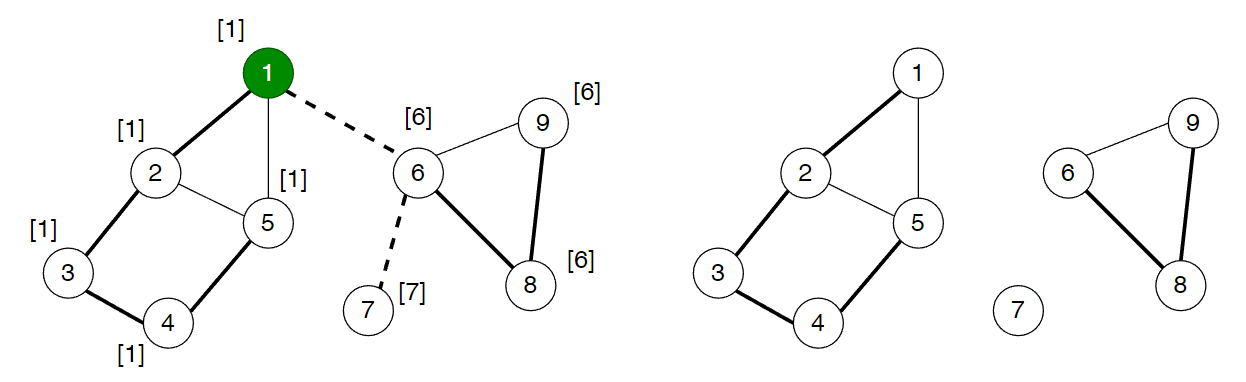
在具体的程序实现中，一般先用 Tarjan 算法标记出所有的桥边。然后，再对整个无向图执行一次深度优先遍历(遍历的过程中不访问桥边)，划分出每个连通块。下面的代码在 Tarjan 求桥的参考程序基础上，计算出数组 cc ， c[x]c[x] 表示节点所属的“边双连通分量”的编号。

模板题： P6813 无向图的边双连通分量 - TopsCoding

参考代码：

const int N = 5e5+5, M = 2e6+5;
int head[N], ver[M*2], nxt[M*2];
int dfn[N], low[N], n, m, tot = 1, num;
bool bridge[N*2];
int c[N], dcc;
vector<int> ans[N];void add(int x, int y) {ver[++tot] = y;nxt[tot] = head[x];head[x] = tot;
}void tarjan(int x, int in_edge) {dfn[x] = low[x] = ++num;for(int i = head[x]; i; i = nxt[i]) {int y = ver[i];if(!dfn[y]) {tarjan(y, i);low[x] = min(low[x], low[y]);if(low[y] > dfn[x]) { // 是割边（桥）bridge[i] = bridge[i^1] = true;}} // 否则，不是搜索树边，且不是同一条边else if(i != (in_edge^1)) {low[x] = min(low[x], dfn[y]);}}
}void dfs(int u) {ans[dcc].push_back(u);c[u] = dcc;for(int i = head[u]; i; i = nxt[i]) {int v = ver[i];if(!c[v] && !bridge[i])dfs(v);}
}int main(){cin >> n >> m;while(m--) {int x, y;cin >> x >> y;add(x, y); add(y, x);}for(int i = 1; i <= n; i++) {if(!dfn[i]) tarjan(i, 0);}for(int i = 1; i <= n; i++) {if(!c[i])++dcc, dfs(i);}cout << dcc << '\n';for(int i = 1; i <= dcc; i++) {cout << ans[i].size() << ' ';for(auto x : ans[i])cout << x << ' ';cout << '\n';}return 0;
}

e-DCC 的缩点

把每个 e-DCC 看作一个节点，把桥边 (x,y)(x,y) 看作连接编号为 c[x]c[x] 和 c[y]c[y] 的 e-DCC 对应节点的无向边，会产生一棵树(若原来的无向图不连通，则产生森林)。这种把 e-DCC 收缩为一个节点的方法就称为“缩点”。下面的代码在 Tarjan 求桥 e-DCC 的参考程序基础上，把 e-DCC 缩点，构成一新的树(或森林)，存储在另一个邻接表中。

const int N = 5e5+5, M = 2e6+5;
int head[N], ver[M*2], nxt[M*2];
int dfn[N], low[N], n, m, tot = 1, num;
bool bridge[N*2];
int c[N], dcc;  // c[i]: 结点 i 所属边双连通分量编号
vector<int> ans[N];
int hc[N], vc[M*2], nxtc[M*2], totc = 1;
void add(int x, int y) {ver[++tot] = y;nxt[tot] = head[x];head[x] = tot;
}
void add_c(int x, int y) {vc[++totc] = y;nxtc[totc] = hc[x];hc[x] = totc;
}void tarjan(int x, int in_edge) {dfn[x] = low[x] = ++num;for(int i = head[x]; i; i = nxt[i]) {int y = ver[i];if(!dfn[y]) {tarjan(y, i);low[x] = min(low[x], low[y]);if(low[y] > dfn[x]) { // 是割边（桥）bridge[i] = bridge[i^1] = true;}} // 否则，不是搜索树边，且不是同一条边else if(i != (in_edge^1)) {low[x] = min(low[x], dfn[y]);}}
}void dfs(int u) {//ans[dcc].push_back(u);c[u] = dcc;for(int i = head[u]; i; i = nxt[i]) {int v = ver[i];if(!c[v] && !bridge[i])dfs(v);}
}int main(){cin >> n >> m;while(m--) {int x, y;cin >> x >> y;add(x, y); add(y, x);}for(int i = 1; i <= n; i++) {if(!dfn[i]) tarjan(i, 0);}for(int i = 1; i <= n; i++) {if(!c[i])++dcc, dfs(i);}// 新建缩点后的图for(int i = 2; i <= tot; i++) {int x = ver[i^1], y = ver[i];if(c[x] == c[y]) continue;  // 在同一个连通块add_c(c[x], c[y]);}cout << "缩点后点数：" << dcc << '\n';cout << "缩点后边数（可能有重边）：" << totc / 2 << '\n';for(int i = 2; i <= totc; i++)cout << vc[i^1] << ' ' << vc[i] << '\n';return 0;
}

v-DCC的求法

点双连通分量是一个极其容易误解的概念。它与删除割点后图中剩余的连通块是不一样的，请格外留意。

若每个节点为孤立点，则它自己单独构成一个 v-DCC。除了孤立点之外，点双连通分量的大小至少为 22 。根据 v-DCC 定义中的“极大”性，虽然桥（割边）不属于任何 e-DCC（边双连通分量），但是割点可能属于多个 v-DCC。下面的无向图共有 22 个割点， 44 个点双连通分量。

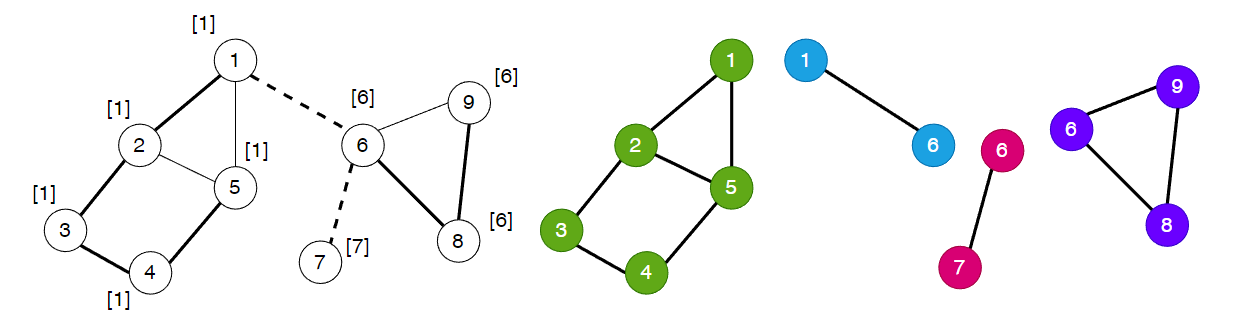
我们考虑使用上面的 dfndfn 和 lowlow 来求，我们将深度优先遍历时遇到的所有边加入到栈里面，当找到一个割点的时候，就将这个割点往下走到的所有边弹出，而这些边所连接的点就是一个点双连通分量了。

具体来说，需要在 Tarjan 算法的过程中维护一个栈，并按照如下方法维护栈中的元素：

当一个节点 第一次 被访问时，把该节点入栈。
当割点判定法则中的条件 dfn[x]≤low[y]dfn[x]≤low[y] 成立时，此时 xx 是割点， subtree(y)subtree(y) 为一个点双连通分量。为了得到 subtree(y)subtree(y) ，无论 xx 是否为根 ，都要将 subtree(y)subtree(y) 弹出，具体操作如下：
（1）栈顶为 subtree(y)subtree(y) 的最底端（最深处），从栈中不断弹出节点，直至节点 yy 被弹出（ yy 要弹出 ）。
（2）刚才弹出的所有节点 与节点 xx 一起构成一个 v-DCC。

下面的程序在求出割点的同时，计算出 vector 数组 dccdcc ， dcc[i]dcc[i] 保存编号为 ii 的 v-DCC 中的所有节点。

模板题： P6814 无向图的点双连通分量 - TopsCoding

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5, M = 2e6+5;
int head[N], ver[M * 2], Next[M * 2];
int dfn[N], low[N], num, stk[N], top;
int n, m, tot = 1, root, cnt;
bool cut[N];
vector<int> dcc[N * 2];//dcc[i] 存储编号为 i 的 v-DCC 中的所有节点
void add(int x, int y) {//邻接表存图ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}
void tarjan(int x) {dfn[x] = low[x] = ++num;stk[++top] = x;if (x == root && head[x] == 0) { //孤立点dcc[++cnt].push_back(x);return;}int flag = 0;for (int i = head[x]; i; i = Next[i]) {int y = ver[i];if (!dfn[y]) {tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]) {flag++;if(x != root || flag > 1) cut[x] = true;cnt++;int z;do {z = stk[top--];dcc[cnt].push_back(z);} while (z != y);dcc[cnt].push_back(x);}} elselow[x] = min(low[x], dfn[y]);}
}
int main() {cin >> n >> m;for (int i = 1; i <= m; i++) {int x, y;cin >> x >> y;if (x == y)continue;add(x, y), add(y, x);}for (int i = 1; i <= n; i++)if (!dfn[i])root = i, tarjan(i);cout << cnt << "\n";for (int i = 1; i <= cnt; i++) { //输出cout << dcc[i].size();for (int j = 0; j < dcc[i].size(); j++)cout << ' ' << dcc[i][j];cout << "\n";}return 0;
}

v-DCC 的缩点

v-DCC 的缩点比 e-DCC 要复杂一些一一因为一个割点可能属于多个 v-DCC。设图中共有 pp 个割点和 tt 个 v-DCC。我们建立一张含 p+tp+t 个节点的新图，把每个 v-DCC 和每个割点都作为新图中的节点，并在每个割点与包含它的所有 v-DCC 之间连边。容易发现，这张新图其实是一棵树(或森林)，如下图所示：

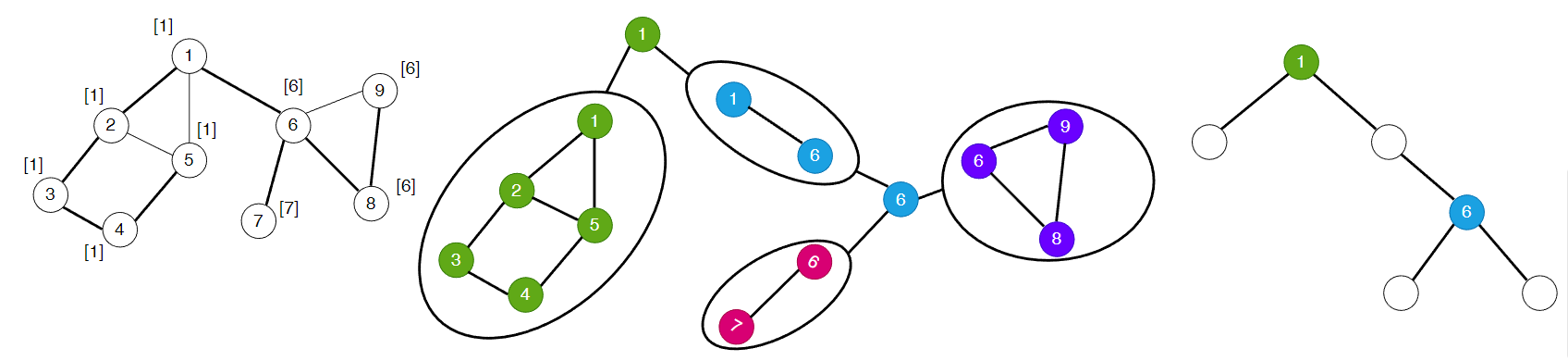
下面的代码在 Tarjan 求割点和 v-DCC 的参考程序的 main 函数基础上，对 v-DCC 缩点，构成一棵新的树(或森林)，存储在另一个邻接表中。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5, M = 2e6+5;
int head[N], ver[M * 2], nxt[M * 2];
int dfn[N], low[N], num, stk[N], top;
int n, m, tot = 1, root, cnt;  // cnt: 割点数量
bool cut[N];
vector<int> dcc[N * 2];//dcc[i] 存储编号为 i 的 v-DCC 中的所有节点
int hc[N], vc[M*2], nxtc[M*2], totc = 1;
int c[N], new_id[N];void add(int x, int y) {//邻接表存图ver[++tot] = y;nxt[tot] = head[x];head[x] = tot;
}
void add_c(int x, int y) {vc[++totc] = y;nxtc[totc] = hc[x];hc[x] = totc;
}void tarjan(int x) {dfn[x] = low[x] = ++num;stk[++top] = x;if (x == root && head[x] == 0) { //孤立点dcc[++cnt].push_back(x);return;}int flag = 0;for (int i = head[x]; i; i = nxt[i]) {int y = ver[i];if (!dfn[y]) {tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]) {flag++;if(x != root || flag > 1) cut[x] = true;cnt++;int z;do {z = stk[top--];dcc[cnt].push_back(z);} while (z != y);dcc[cnt].push_back(x);}} elselow[x] = min(low[x], dfn[y]);}
}
int main() {cin >> n >> m;for (int i = 1; i <= m; i++) {int x, y;cin >> x >> y;if (x == y)continue;add(x, y), add(y, x);}for (int i = 1; i <= n; i++)if (!dfn[i])root = i, tarjan(i);// 给每个割点一个新的编号num = cnt;for(int i = 1; i <= n; i++)if(cut[i]) new_id[i] = ++num;// 建新图，从每个 v-DCC 到它包含的所有割点连边for(int i = 1; i <= n; i++) {for(auto x : dcc[i]) {if(cut[x]) {add_c(i, new_id[x]);add_c(new_id[x], i);}else c[x] = i; // 除割点外，其它点仅属于一个 v-DCC}}printf("缩点后的森林的点数：%d，边数 %d\n", num, totc/2);printf("编号 1~%d 为原图的 v-DCC，>%d 的为原图割点\n", cnt, cnt);for(int i = 2; i < totc; i += 2)printf("%d %d\n", vc[i^1], vc[i]);return 0;
}