【LeetCode Solutions】LeetCode 热题 100 题解（1 ~ 5）

哈希 - LeetCode 1. 两数之和（简单）

【题目描述】

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

【示例 1】

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

【示例 2】

输入：nums = [3,2,4], target = 6
输出：[1,2]

【示例 3】

输入：nums = [3,3], target = 6
输出：[0,1]

【提示】

$2\le nums.length\le 10^4$
$-10^9\le nums[i]\le 10^9$
$-10^9\le target\le 10^9$

---

【分析】

维护一个哈希表，记录 $nums[1]\sim nums[i-1]$，当遍历到 $nums[i]$ 时，通过哈希表查找是否存在 $target-nums[i]$，如果存在说明找到答案。

---

【代码】

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int, int> st;  // 维护 nums[i] 及其下标for (int i = 0; i < nums.size(); i++) {int x = target - nums[i];if (st.count(x)) return { st[x], i };st[nums[i]] = i;}return {};  // 为了防止编译出问题}
};

哈希 - LeetCode 49. 字母异位词分组（中等）

【题目描述】

给你一个字符串数组，请你将字母异位词组合在一起。可以按任意顺序返回结果列表。

字母异位词是由重新排列源单词的所有字母得到的一个新单词。

【示例 1】

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

【示例 2】

输入: strs = [""]
输出: [[""]]

【示例 3】

输入: strs = ["a"]
输出: [["a"]]

【提示】

$1\le strs.length\le 10^4$
$0\le strs[i].length\le 100$
strs[i] 仅包含小写字母

---

【分析】

我们可以将每个字符串按字典序排序，这样如果两个字符串所含的字符相同那么排序后的字符串一定也相同，然后我们再用一个哈希表记录每类字符串即可。

---

【代码】

class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {vector<vector<string>> res;unordered_map<string, int> st;  // 记录每一类的下标int idx = 0;for (auto s: strs) {string t = s;sort(t.begin(), t.end());if (!st[t]) st[t] = ++idx, res.push_back(vector<string>{s});else res[st[t] - 1].push_back(s);  // 注意 vector 中下标从 0 开始}return res;}
};

哈希 - LeetCode 128. 最长连续序列（中等）

【题目描述】

给定一个未排序的整数数组 nums，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 $O(n)$ 的算法解决此问题。

【示例 1】

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

【示例 2】

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

【示例 3】

输入：nums = [1,0,1,2]
输出：3

【提示】

$0<=nums.length<=10^5$
$-10^9<=nums[i]<=10^9$

---

【分析】

首先用哈希表记录下每个数是否存在，然后按照任意顺序枚举每个数，假如枚举到 $x$，然后我们就不断查看 $x+1,x+2,\dots ,y$ 是否存在，直到 $y+1$ 不存在，那么连续序列的长度就为 $y-x+1$。

但如果每次都这样枚举时间复杂度为 $O(n^2)$，需要优化，我们只枚举每段连续序列的起点，也就是最小值，如果 $x-1$ 存在说明 $x$ 肯定不是最长连续序列的起点，就不用枚举了。

此外还需要进行判重，对于遍历过的序列将其从哈希表中删去，保证每个数只被枚举一次，这样时间复杂度就为 $O(n)$。

---

【代码】

class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> st(nums.begin(), nums.end());for (int num: nums) st.insert(num);int res = 0;for (int num: nums)if (st.count(num) && !st.count(num - 1)) {  // num 为连续序列的起点int x = num;while (st.count(x)) st.erase(x++);  // 将 num 为起点的连续序列从哈希表中删去res = max(res, x - num);}return res;}
};

双指针 - LeetCode 283. 移动零（简单）

【题目描述】

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意，必须在不复制数组的情况下原地对数组进行操作。

【示例 1】

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

【示例 2】

输入: nums = [0]
输出: [0]

【提示】

$1<=nums.length<=10^4$
$-2^{31}<=nums[i]<=2^{31}-1$

进阶：你能尽量减少完成的操作次数吗？

---

【分析】

非常简单的双指针算法，一个指针 $i$ 从前往后遍历数组，另一个指针 $k$ 从前往后存储非零元素，如果 $nums[i]$ 非零，就将其移动到位置 $k$ 上。

---

【代码】

class Solution {
public:void moveZeroes(vector<int>& nums) {for (int i = 0, k = 0; i < nums.size(); i++)if (nums[i]) swap(nums[i], nums[k++]);}
};

双指针 - LeetCode 11. 盛最多水的容器（中等）

【题目描述】

给定一个长度为 n 的整数数组 height。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

【示例 1】

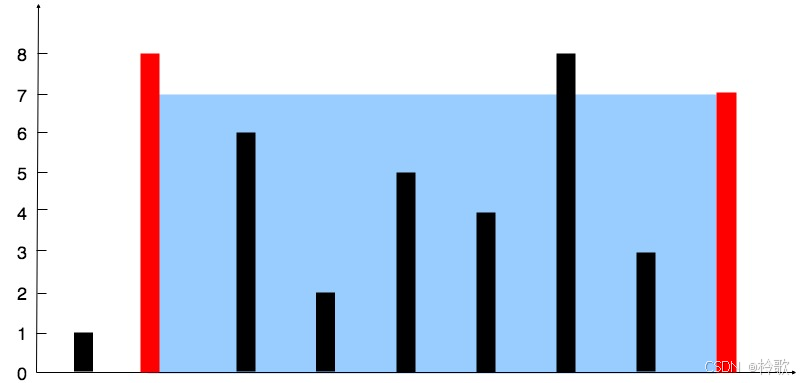
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

【示例 2】

输入：height = [1,1]
输出：1

【提示】

$n=height.length$
$2\le n\le 10^5$
$0\le height[i]\le 10^4$

---

【分析】

很巧妙的一道贪心思维题，我们先在最左边和最右边设置两个指针，每次将指针指向的数较小的那个指针往中间靠拢一格，且每次都维护一遍最大值即可。

因为当一个指针往中间移动时，矩形的宽度缩小了，想要面积变大，那肯定需要指针指向的数值（即矩形高度）变大，而矩形的高度的瓶颈在于较短的那一条边，因此移动较小的指针。

---

【代码】

class Solution {
public:int maxArea(vector<int>& height) {int res = 0;for (int l = 0, r = height.size() - 1; l < r; ) {res = max(res, (r - l) * min(height[l], height[r]));if (height[l] < height[r]) l++;else r--;}return res;}
};