统计学习方法的三要素

假设你是一个外卖配送平台的调度员。你的目标是最小化所有骑手完成所有订单的总配送时间。

• 决策变量 (x)： 如何将订单分配给骑手？骑手按什么顺序送餐？这些分配和路径选择就是你的决策变量。

• 目标函数 (f(x))： 一个计算函数，输入是你的分配方案和路径方案，输出就是所有骑手完成所有订单所花费的总时间。这个总时间函数 f(x) 就是你的目标函数，你需要最小化它。

• 约束条件： 每个订单必须被送达；骑手一次只能送一个订单（或有限个）；订单必须在承诺时间内送达；骑手不能超速行驶等等。

在这个例子中，目标函数（总配送时间）清晰地定义了你追求的目标（最快送达），优化算法会尝试不同的订单分配和路径规划方案（改变 x），计算每种方案下的 f(x)，最终找出能使得 f(x) 最小的那个方案。

一、监督学习：模型

参数空间即是：所有w和b组成的一个空间。

 二、监督学习：策略

其中：Y表示真实值，f(X)表示输入X，经过模型预测函数f得到的预测值。

风险函数对损失函数求期望。由于联合概率P(x,y)并不是已知的，所以风险函数并不能直接求得，因此选择经验风险替代风险函数。

常见的损失函数

0-1损失函数主要针对的是分类问题、平方损失函数和绝对损失函数主要针对的是回归问题、对数损失函数主要针对的是概率问题。

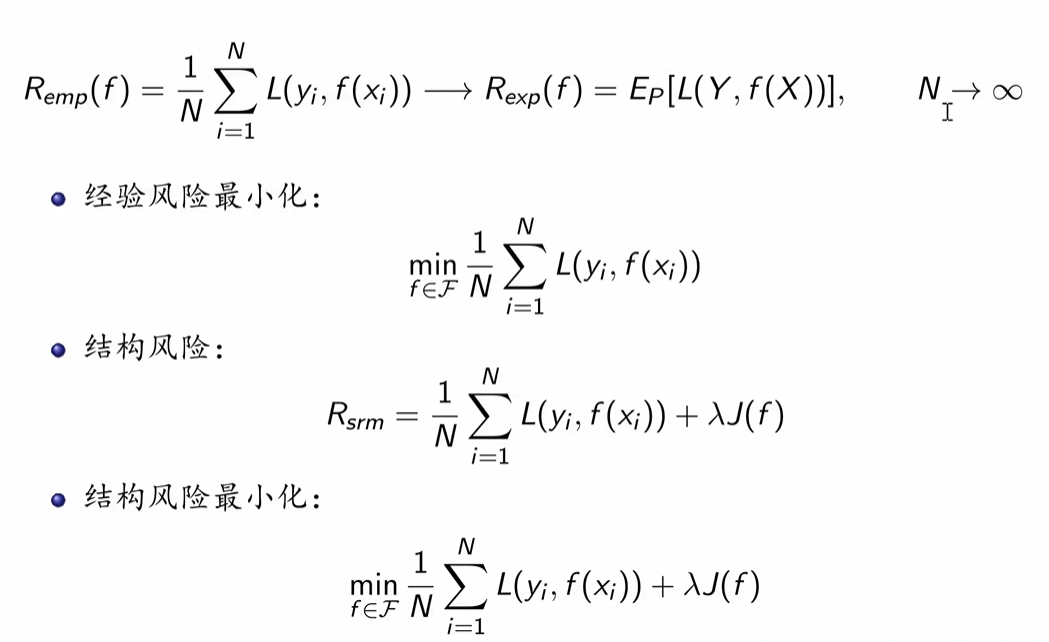
根据大数定律，当N趋于无穷时，经验风险就趋于风险函数。因此用经验风险替代风险函数是有依据的。但是在实际问题中，N往往是有限的。所以仅仅使用经验风险替代风险函数是不太理想的。因此需要对经验风险进行校正。

策略一：经验风险最小化

当N足够大时，我们可以认为经验风险是风险函数的一个估计值。这种情况下，只要选择使经验风险最小的模型即可。

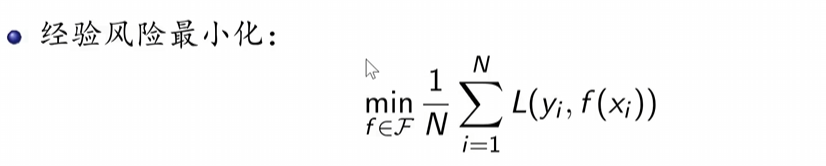
策略二：结构风险最小化

当N不够大时，将经验风险作为风险函数的估计值会造成过拟合现象。于是引入结构风险。

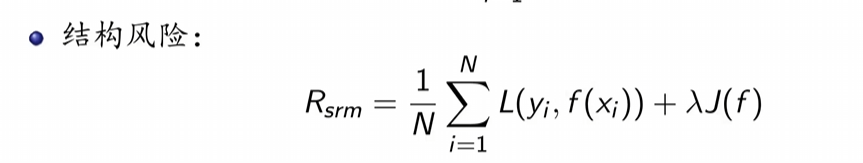
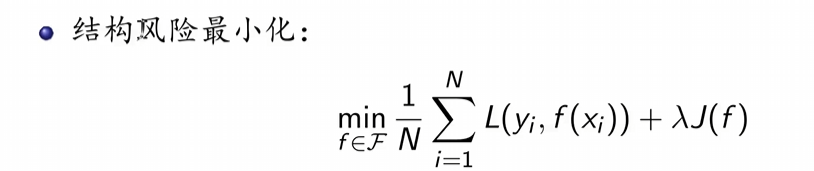
三、监督学习：算法

• 算法：如何求解最优模型的问题
• 若优化问题存在显示解析解，算法简易
• 通常不存在解析解，需要数值计算方法，比如梯度下降法