当前位置：首页 > ops >正文

粒子群优化（Particle Swarm Optimization, PSO）

ops 2025/7/22 14:13:58

粒子群优化是一种基于群体智能的优化算法，由Kennedy和Eberhart于1995年提出，灵感来源于鸟群或鱼群在觅食时通过信息共享协作寻找最优位置的行为。

一 PSO的基本原理

群体中的个体（粒子）通过共享自身经验和群体经验，不断调整自身的位置，最终逼近最优解。

适用于连续型优化问题（如函数优化、参数调优等），也可扩展至离散问题。

粒子：代表解空间中的一个潜在解，包含以下属性：

（1）位置：当前解的位置，即优化问题的候选解。

（2）速度：粒子在解空间中移动的方向和步长。

（3）个体最优：粒子自身历史最优位置。

（4）全局最优：群体中所有粒子的历史最优位置。

二算法步骤

2.1 初始化：

随机生成一组粒子的位置和速度（初始解）

设定群体大小、搜索空间维度和参数，下面详细了解一下：

搜索空间维度对应优化问题中变量的个数：

eg：优化函数 $f(x_1, x_2)$ 是二维问题，优化一个包含10个参数的模型则是十维问题。

在工程应用中就可以按照机械设计中的材料参数来设定（三维：长度、厚度、密度）

参数：

（1）群体大小（粒子数量）：群体越大，搜索能力越强，但计算成本增加，一般是20~50粒子。

（2）惯性权重 $w$ ：控制粒子的搜索方法：

$w$ 较大时，粒子偏向全局搜索（探索新区域）。

$w$ 较小时，偏向局部精细搜索（开发已知区域）。

$w$ 可以设定为固定值，但是设置成动态调整的更好：初始阶段 $w = 0.9$ → 逐渐线性递减至 $w = 0.4$ ，全局到局部。

（3）加速常数 $c_1$ 和 $c_2$

$c_1$ （个体认知系数）：粒子向自身历史最优位置的学习强度。

$c_2$ （社会学习系数）：粒子向群体全局最优位置的学习强度。

设定数值：

经典设置（标准PSO）： $c_1$ = 2.0 $c_2$ =2.0（需 w<1 避免发散）。

$c_1$ + $c_2$ ≤ 4.0（稳定性条件）

自适应调整：早期强调个体探索（ $c_1$ 较大），后期增加群体协作（ $c_2$ 较大）。

（4）最大速度 $v_{\text{max}}$

限速防止粒子失控（如超出搜索空间）。

通常设置为每个维度对应变量范围的10%~20%。

eg：若变量范围是 x∈[−5,5] ，则 $v_{\text{max}} = 1.0$ 。

（5）迭代次数与终止条件

控制算法何时停止。

设定方法：

固定迭代次数：如100~1000次（根据问题复杂度调整）。

动态终止：适应度连续多代（如20代）无显著改进。

（6）其他参数

初始位置与速度：

通常在搜索空间内随机均匀分布。

若问题有先验知识，可集中初始化到可能最优区域附近。

邻域拓扑：

全局拓扑（全连接）：粒子共享全局最优 gBest（经典PSO）。

gBest：表示整个粒子群的历史最优位置。

局部拓扑（如环形或星型）：仅与邻居共享信息（减缓收敛，避免局部最优）。

2.2计算适应度

根据目标函数评估每个粒子的适应度（性能）。

适应度是目标问题的量化表现，直接反映粒子当前位置（候选解）的性能。

适应度函数通常是优化问题的目标函数或其变体。

（1）目标函数的直接映射

方法：直接使用优化问题的目标函数值作为适应度。

示例：最小化函数 $f(x) = x^2$ → 适应度 $Fitness = x^2$

（2）目标函数的转换

当目标函数的值域不适合直接比较时，需进行转换：

倒数法（最小化问题）： $Fitness = \frac{1}{1 + f(x)}$ 避免目标函数值为 0 时出现无穷大。

缩放和平移：例如将结果归一化到 [0,1] 区间。

（3）多目标问题的适应度

若问题有多个优化目标，需转换为单目标适应度：

加权求和法： $Fitness = \sum_{i=1}^n w_i \cdot f_i(x)$ 其中 $w_i$ 是权重系数，反映各子目标的重要性。

Pareto 前沿法：在多目标PSO中，通过非支配排序确定粒子的适应度等级。

(4) 约束条件的处理

对于带有约束的优化问题（如 $g_i(x) \leq 0$ ），需在适应度中惩罚不可行解。

罚函数法：

$Fitness = f(x) + \sum_{i=1}^k \lambda_i \cdot \max(0, g_i(x))$

$\lambda_i$ 是惩罚系数，约束被违反时增加适应度值（最小化问题）以降低选中概率。

可行性优先法则：可行解的适应度优于所有不可行解。

步骤：

初始化粒子位置：在解空间中随机生成粒子的初始位置。

计算每个粒子的目标函数值：根据具体问题求解 f(x)

转换为适应度值：按需调整（如取倒数、加符号）以适应最大化或最小化需求。

约束处理：若存在约束条件，通过罚函数修正适应度值。

记录最优值：将当前适应度与个体历史最优（pBest）和全局最优（gBest）比较，决定是否更新。

2.3更新个体最优（pBest）

若当前位置优于个体历史最优值，则更新 pBest = 当前位置。

2.4更新全局最优（gBest）

选择适应度最好的粒子，更新群体全局最优 gBest。

2.5更新速度和位置

速度更新公式：

$v_{i}(t+1) = w \cdot v_{i}(t) + c_1 \cdot r_1 \cdot (pBest_i - x_i(t)) + c_2 \cdot r_2 \cdot (gBest - x_i(t))$

位置更新公式：

$x_{i}(t+1) = x_{i}(t) + v_{i}(t+1)$

$w$ ：惯性权重（控制保留原速度的比例）。

$c_1, c_2$ ：个体认知和社会学习的加速因子（通常 $c_1 + c_2 \leq 4$ ）。

$r_1, r_2$ ：0到1之间的随机数（增加随机性）。

那我们更新速度和位置的作用是什么呢？

速度更新：动态平衡探索（全局搜索）与开发（局部优化），指导粒子的移动方向。

位置更新：根据速度实际移动粒子，生成新候选解，并触发反馈机制。

两者结合使PSO能够高效覆盖解空间，最终收敛到全局或局部最优解。

2.6终止条件

达到最大迭代次数、适应度无明显改进或满足精度要求时停止。

三优缺点分析

优点：

（1）原理简单，实现容易。

（2）参数少，收敛速度较快。

（3）适用于高维、非线性问题。

缺点：

（1）易陷入局部最优。

（2）对参数敏感（需调节 $w, c_1, c_2$ ）。

（3）不保证全局最优解。

四常见变体

（1）标准PSO：基础版本，无惯性权重。

（2）带惯性权重的PSO（PSO-W）：引入动态变化的 w。

（3）混合PSO：与其他算法结合（如遗传算法、模拟退火）。

（4）多目标PSO：针对多目标优化问题。

（5）自适应PSO：根据群体状态动态调整参数。

五应用实例

函数优化：寻找复杂函数的最小值/最大值。

神经网络训练：优化权重参数。

工程优化：结构设计、路径规划、电力系统调度。

特征选择：在机器学习中筛选最优特征子集。

简单代码示例：

import numpy as np# 定义目标函数（示例函数：Sphere函数，最小值为0，最优解为全0向量）
def fitness_function(position):return np.sum(position**2)# PSO算法类
class ParticleSwarmOptimizer:def __init__(self, num_particles, dimensions, bounds, max_iter, w=0.5, c1=1.5, c2=1.5):self.num_particles = num_particles  # 粒子数量self.dimensions = dimensions        # 解空间维度self.bounds = bounds                # 搜索空间范围 [min, max]self.max_iter = max_iter            # 最大迭代次数self.w = w                          # 惯性权重self.c1 = c1                        # 个体学习因子self.c2 = c2                        # 群体学习因子# 初始化粒子群self.particles = []for _ in range(num_particles):position = np.random.uniform(bounds[0], bounds[1], dimensions)velocity = np.random.uniform(-1, 1, dimensions)  # 初始速度随机生成pbest_position = position.copy()pbest_value = fitness_function(position)self.particles.append({'position': position,'velocity': velocity,'pbest_position': pbest_position,'pbest_value': pbest_value})# 初始化全局最优解self.gbest_value = float('inf')self.gbest_position = np.zeros(dimensions)for p in self.particles:if p['pbest_value'] < self.gbest_value:self.gbest_value = p['pbest_value']self.gbest_position = p['pbest_position'].copy()def optimize(self):for iter in range(self.max_iter):for p in self.particles:# 更新速度r1 = np.random.rand(self.dimensions)r2 = np.random.rand(self.dimensions)velocity = (self.w * p['velocity'] +self.c1 * r1 * (p['pbest_position'] - p['position']) +self.c2 * r2 * (self.gbest_position - p['position']))p['velocity'] = velocity# 更新位置p['position'] += p['velocity']# 边界检查（防止越界）p['position'] = np.clip(p['position'], self.bounds[0], self.bounds[1])# 计算适应度current_value = fitness_function(p['position'])# 更新个体最优pBestif current_value < p['pbest_value']:p['pbest_position'] = p['position'].copy()p['pbest_value'] = current_value# 更新全局最优gBestif current_value < self.gbest_value:self.gbest_value = current_valueself.gbest_position = p['position'].copy()# 打印当前迭代结果if (iter + 1) % 10 == 0:print(f"Iteration {iter + 1}, Best Value: {self.gbest_value:.4f}")return self.gbest_position, self.gbest_value# 设置参数
num_particles = 30
dimensions = 5   # Sphere函数的维度（例如5维）
bounds = [-5, 5] # 搜索空间范围 [-5, 5]
max_iter = 100# 运行PSO
pso = ParticleSwarmOptimizer(num_particles, dimensions, bounds, max_iter, w=0.7, c1=1.5, c2=1.5)
best_position, best_value = pso.optimize()# 输出结果
print("\n----- Final Result -----")
print(f"Best Position: {best_position}")
print(f"Best Value: {best_value:.6f}")

只需修改 fitness_function 的定义，就可以替换其他目标函数。

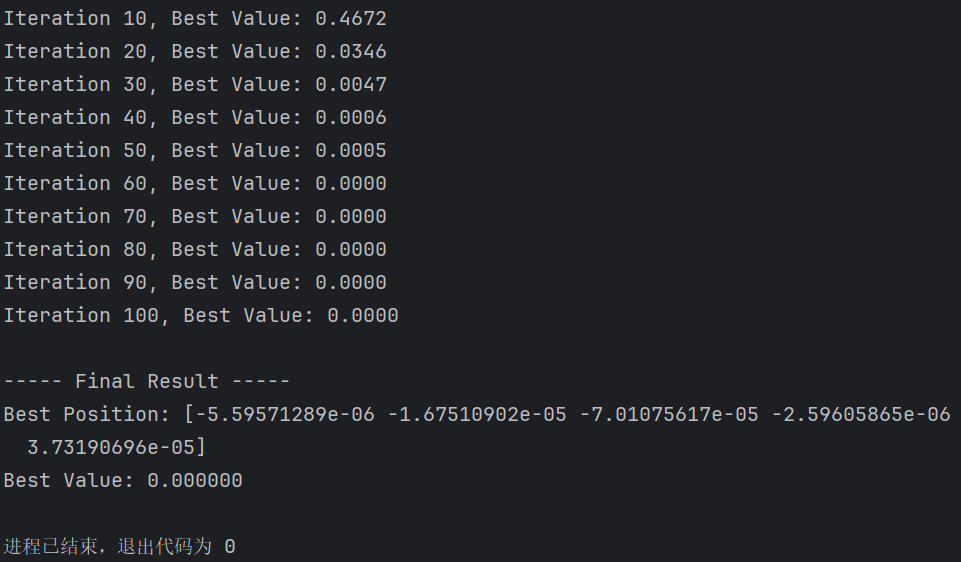
上述代码输出：