【C++高阶一】二叉搜索树

1.什么是二叉搜索树

任何一个节点，他的左子树的所有节点都比他小，右子树的所有节点都比他大

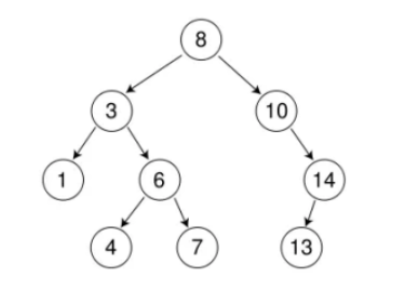
二叉搜索树是有序的，中序遍历这棵二叉搜索树刚好是升序
时间复杂度为O(N)，因为会出现这种极端情况

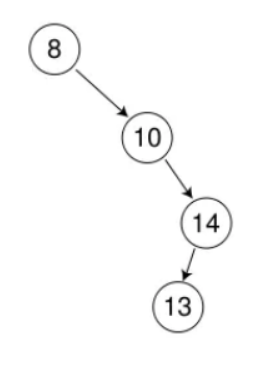
二叉搜索树中不能出现值相同的节点

2.二叉搜索树非递归实现

大致框架

template<class K>
struct BSTreeNode //二叉搜索树节点
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};template<class K>
class BSTree//二叉搜索树
{typedef BSTreeNode<K> Node;
public:private:Node* _root = nullptr;
};

2.1插入

插入的值比根大就往右走，比根小就往左走，如果遇见和插入值相同的值就返回false

bool insert(const k& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else {parent->_right = cur;}return true;}

parent保存每一步的父节点，在插入之后起到父子节点连接作用

2.2删除

2.2.1删除分析一

1. 被删除节点无孩子：
   直接将此节点删除，不用做特殊处理
2. 被删除节点只有左孩子：
   此节点被删除后，将此节点的左孩子连接到此节点的父亲节点
3. 被删除节点只有右孩子：
   此节点被删除后，将此节点的右孩子连接到此节点的父亲节点

bool erase(const k& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if(cur->_key > key){parent = cur;cur = cur->_right;}else//找到了{if (cur->_left == nullptr)//左孩子为空{if (cur == _root)_root = cur->_right;else{if (cur == parent->_right)parent->_right = cur->_right;elseparent->_left = cur->_right;}delete cur;}else if (cur->_right == nullptr)//右孩子为空{if (cur == _root)_root = cur->_left;else{if (cur == parent->_right)parent->_right = cur->_leftelseparent->_left = cur->_left;}delete cur;}//第四种情况 //else{}}}return false；
}

表面只写了两种情况，其实已经把无孩子的情况包括了

2.2.2删除分析二

当被删除的节点存在左右孩子时，我们要使用替换法
被替换的节点一定要满足一个条件:
是左子树的最大值 || 是右子树的最小值

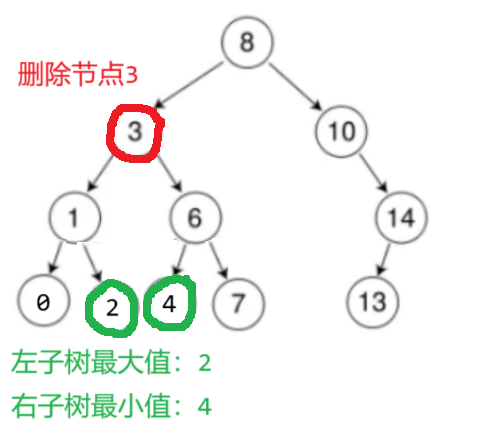
假设使用右子树中最小的节点来替换，其左孩子为空，但右孩子未知，还需要分情况讨论

else//左右孩子都不为空
{//用右子树最小值来替换Node* Temp_parent = cur;//临时父节点Node* R_subtree_min = cur->_right;//右子树最小值while (R_subtree_min->_left){Temp_parent = R_subtree_min;R_subtree_min = R_subtree_min->_left;}swap(cur->_key, R_subtree_min->_key);if (R_subtree_min == Temp_parent->_left){Temp_parent->_left = R_subtree_min->_right;}else{Temp_parent->_right = R_subtree_min->_right;}delete R_subtree_min;
}

2.3查找

bool find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}

3.二叉搜索树递归实现

递归实现全都使用了函数嵌套的方式，是为了使用_root这个定义在类中的成员变量

3.1插入

插入的基本思路一样,但递归到空时构建新节点的链接有三种方式：
1.多传一个参数，记录父节点
2.递归到空节点的上一层，比如if(root->_left==NULL) 开始构建节点
3.传引用
前两个方法和循环写法没什么区别，下面都使用传引用

bool Re_insert(const K& key)
{return _Re_insert(_root, key);
}bool _Re_insert(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}if (root->_key > key){return _Re_insert(root->_left, key);}else if (root->_key < key){return _Re_insert(root->_right, key);}else{return false;}
}

3.2删除

bool Re_erase(const K& key)
{return _Re_erase(_root, key);
}
bool _Re_erase(Node*& root, const K& key)
{if (root == nullptr)return false;if (root->_key > key){return _Re_erase(root->_left, key);}else if (root->_key < key){return _Re_erase(root->_right, key);}else//找到了，准备删除{if (root->_left == nullptr)//左孩子为空{Node* temp = root;root = root->_right;delete temp;return true;}else if (root->_right == nullptr)//右孩子为空{Node* temp = root;root = root->_left;delete temp;return true;}else//左右孩子都不为空{//找右子树的最小值Node* temp = root->_right;while (temp->_left){temp = temp->_left;}swap(root->_key, temp->_key);return _Re_erase(root->_right, key);}}
}

3.3查找

bool Re_find(const K& key)
{return _Re_find(_root, key);
}
private:
bool _Re_find(Node* root,const K& key)
{if (root == nullptr)return false;if (root->_key > kry){return _Re_find(root->_left, key);}else if (root->_key < kry){return _Re_find(root->_right, key);}else{return true;}
}

4.完整代码

template<class K>
struct BSTreeNode //二叉搜索树节点
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};template<class K>
class BSTree//二叉搜索树
{typedef BSTreeNode<K> Node;
public:bool insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else {parent->_right = cur;}return true;}bool erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if(cur->_key < key){parent = cur;cur = cur->_right;}else//找到了,准备删除{if (cur->_left == nullptr)//左孩子为空{if (cur == _root)_root = cur->_right;else{if (cur == parent->_right)parent->_right = cur->_right;elseparent->_left = cur->_right;}delete cur;}else if (cur->_right == nullptr)//右孩子为空{if (cur == _root)_root = cur->_left;else{if (cur == parent->_right)parent->_right = cur->_leftelseparent->_left = cur->_left;}delete cur;}else//左右孩子都不为空{//用右子树最小值来替换Node* Temp_parent = cur;//临时父节点Node* R_subtree_min = cur->_right;//右子树最小值while (R_subtree_min->_left){Temp_parent = R_subtree_min;R_subtree_min = R_subtree_min->_left;}swap(cur->_key, R_subtree_min->_key);if (R_subtree_min == Temp_parent->_left){Temp_parent->_left = R_subtree_min->_right;}else{Temp_parent->_right = R_subtree_min->_right;}delete R_subtree_min;}return true;}}return false;}bool find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;}bool Re_insert(const K& key){return _Re_insert(_root, key);}bool Re_erase(const K& key){return _Re_erase(_root, key);}bool Re_find(const K& key){return _Re_find(_root, key);}
private:bool _Re_insert(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key){return _Re_insert(root->_left, key);}else if (root->_key < key){return _Re_insert(root->_right, key);}else{return false;}}bool _Re_erase(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key > key){return _Re_erase(root->_left, key);}else if (root->_key < key){return _Re_erase(root->_right, key);}else//找到了，准备删除{if (root->_left == nullptr)//左孩子为空{Node* temp = root;root = root->_right;delete temp;return true;}else if (root->_right == nullptr)//右孩子为空{Node* temp = root;root = root->_left;delete temp;return true;}else//左右孩子都不为空{//找右子树的最小值Node* temp = root->_right;while (temp->_left){temp = temp->_left;}swap(root->_key, temp->_key);return _Re_erase(root->_right, key);}}}bool _Re_find(Node* root,const K& key){if (root == nullptr)return false;if (root->_key > kry){return _Re_find(root->_left, key);}else if (root->_key < kry){return _Re_find(root->_right, key);}else{return true;}}
private:Node* _root = nullptr;
};