6.4.2_1最短路径问题_BFS算法

最短路径问题：

单源：一个源头出发到各个其他顶点最短路径 

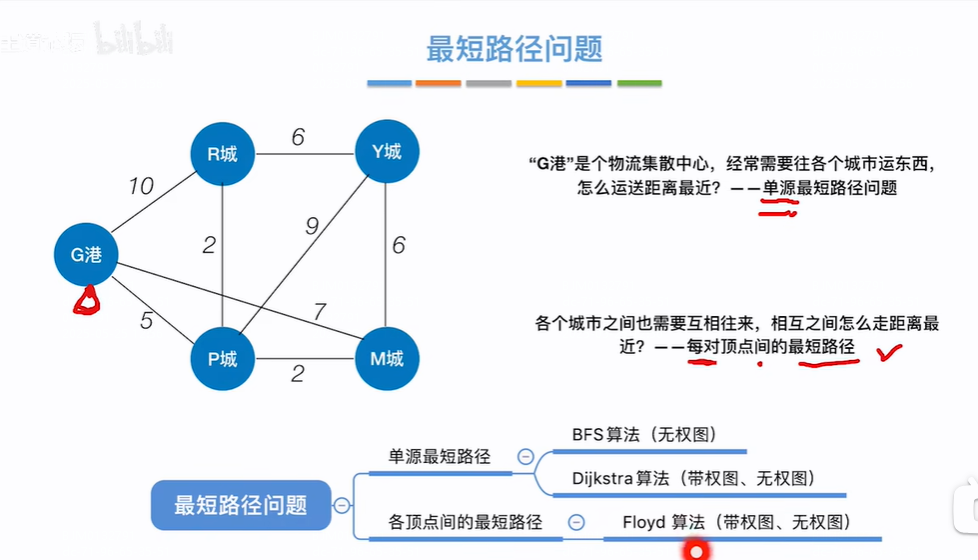
BFS求无权图的单源最短路径：

无权图认为每个边之间的权值都为1，并不是无权

BFS广度优先遍历从2(单源)开始走一遍流程

广度优先遍历BFS解决无权图单源最短路径代码更改：

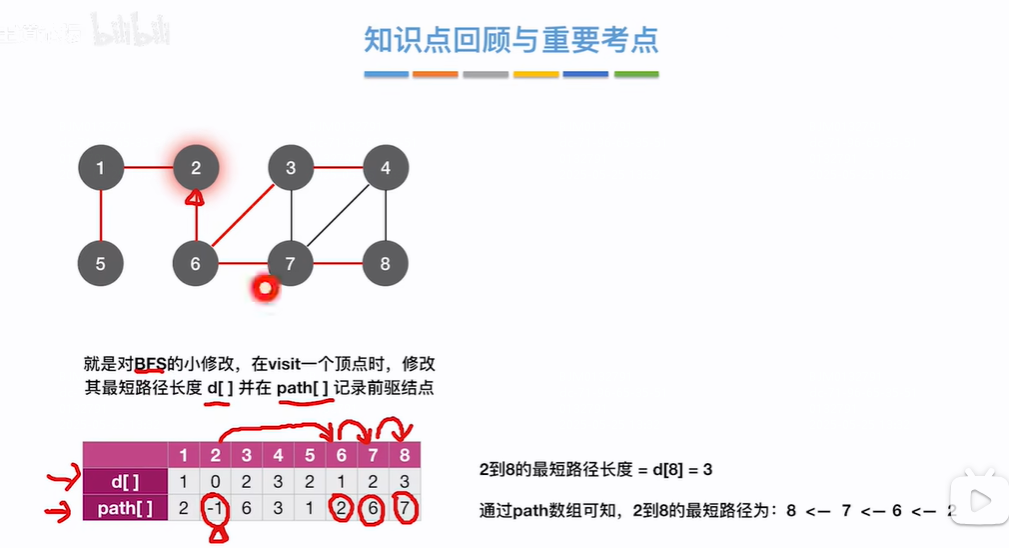
添加了2个数组，d[]用来记录各个顶点到原始顶点的最短记录的长度和path[]记录每个顶点在最短路径上的直接前驱(每个顶点从哪个顶点过来)，把原BFS遍历的while循环中的visited访问代码改成了

过程如下：

单源为2顶点，即u=2，开始for循环把各个顶点到单源的最短记录长度d[]都初始化成∞，把path[]最短路径从哪个顶点过来设为-1，d[u]=0因为2顶点到2顶点路径长度为0，然后开始BFS访问2顶点，2入队，队列不为空进入for循环，2出队开始此时u=2，for循环求2的邻接边顶点w1和6，如果邻接边顶点w没被访问过，开始访问并且设置d[w]=d[u]+1，即下图中的1顶点到单源顶点的路径长度为d[1]=d[2]+1=1，因为是从2顶点直接过来的，即path[1]=u=2，6同，d[6]=1，path[6]=2，然后进行下一轮while循环，此时队头指针在1元素，1出队即u=1，进行查找1的邻接边顶点2和5,2已经被访问跳出for循环，5未被访问即开始访问并且d[5]=d[1]+1=1+1=2，path[5]=u=1，此时队列不为空，队头指针指向6元素，6出队，u=6开始for循环找6的邻接点2、3、7，2已被访问3、7未被访问，开始访问3，即w=3则设置d[]数组和path[]数组，d[w]=d[u]+1即d[3]=d[6]+1=1+1=2，path[w]=path[3]=u=6,3被访问并且入队，另外一个邻接点7没被访问开始访问7，w=7,d[7]=d[6]+1=2,path[7]=6,7被访问且入队，队列不为空开始进行下一轮while循环，队头元素为5,5出队则u=5，此时队头元素指向3，开始找5的邻接点1,1被访问过跳出for循环，队列不为空走下一轮while循环，3出队u=3，开始找3的邻接点4、6、7,6和7已被访问不再访问。。。。。。直到4和8顶点的所有邻接点都已被访问过不再访问d[]和path[]数组都被修改了

21653748

 

知识回顾：

如下最终得到了一个d[]和path[]的值，可以得到各个顶点与单源顶点的最短路径长度+路径序列，如顶点为8的到单源2的最短路径长度为d[8]=3，路径序列求法从当前顶点开始一直往前找path直到找到path的值为单源顶点的整个序列就是该顶点到单源的路径序列，如8顶点：8顶点对应的前驱path[8]=7,path[7]=6，path[6]=2,即找到了单源依次路径序列为8、7、6、2即8<-7<-6<-2（左朝向是因为是求单源到各个顶点的路径长度，所以让单源指向）

通过广度优先遍历可以得到一个广度优先生成树，树的每个节点在第几层也直接反映了2单源到各个顶点的距离，则如果是最短路径的话，通过广度优先遍历构造出来的生成树一定是高度/深度最小的

 

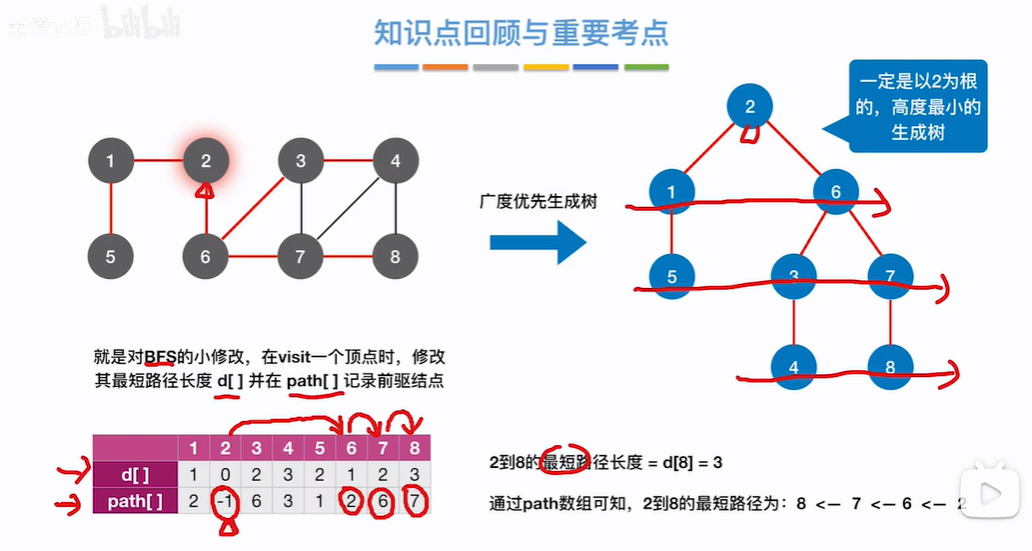
。。。。。。不知道有意义不。。。。。。。