当前位置： 首页 > ops >正文

【数据结构】堆

ops 2025/8/21 5:06:14

本文是小编巩固自身而作，如有错误，欢迎指出！

1.树

1.1树的概念与结构

树是⼀种⾮线性的数据结构，它是由 n（n>=0） 个有限结点组成⼀个具有层次关系的集合。把它叫做 树是因为它看起来像⼀棵倒挂的树，也就是说它是根朝上⽽叶朝下的。

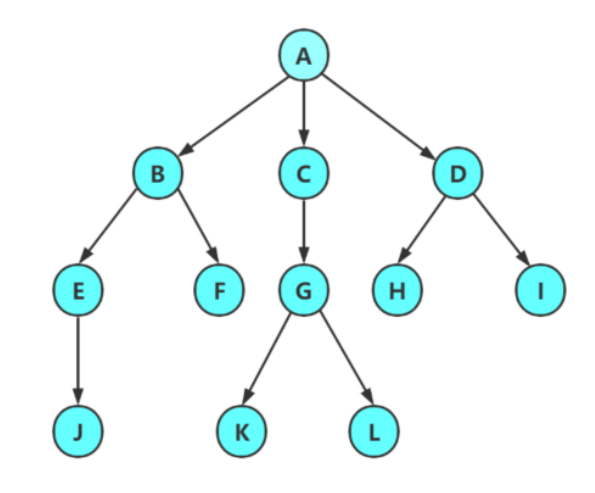
树形结构中，子树之间不能有交集，否则就不是树形结构

⾮树形结构：

因此，我们可以得到 

• 子树是不相交的

• 除了根结点外，每个结点有且仅有⼀个父结点

• ⼀棵N个结点的树有N-1条边

1.2树的一些 相关术语

 

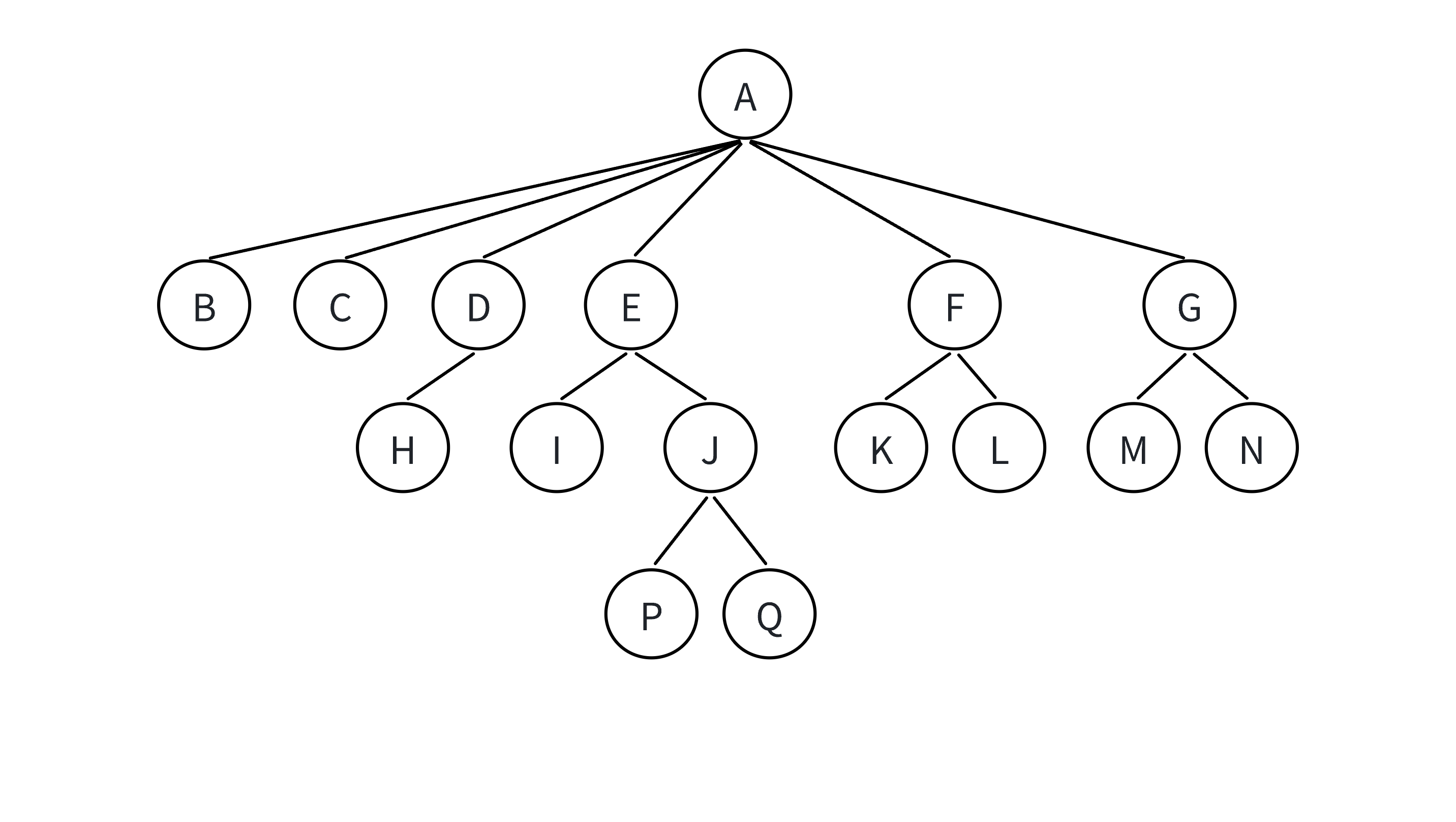
⽗结点/双亲结点：若⼀个结点含有⼦结点，则这个结点称为其⼦结点的⽗结点；如上图：A是B的⽗ 结点

⼦结点/孩⼦结点：⼀个结点含有的⼦树的根结点称为该结点的⼦结点；如上图：B是A的孩⼦结点

结点的度：⼀个结点有⼏个孩⼦，他的度就是多少；⽐如A的度为6，F的度为2，K的度为0 树的度：⼀棵树中，最⼤的结点的度称为树的度；如上图：树的度为 6

 叶⼦结点/终端结点：度为 0 的结点称为叶结点；如上图： B、C、H、I... 等结点为叶结点

分⽀结点/⾮终端结点：度不为 0 的结点；如上图： D、E、F、G... 等结点为分⽀结点

兄弟结点：具有相同⽗结点的结点互称为兄弟结点(亲兄弟)；如上图： B、C 是兄弟结

结点的层次：从根开始定义起，根为第 1 层，根的⼦结点为第 2 层，以此类推；

 树的⾼度或深度：树中结点的最⼤层次；如上图：树的⾼度为 4

结点的祖先：从根到该结点所经分⽀上的所有结点；如上图： A 是所有结点的祖先

路径：⼀条从树中任意节点出发，沿⽗节点-⼦节点连接，达到任意节点的序列；⽐如A到Q的路径为： A-E-J-Q；H到Q的路径H-D-A-E-J-Q

⼦孙：以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙。如上图：所有结点都是A的⼦孙

森林：由 m（m>0） 棵互不相交的树的集合称为森林；

2.二叉树

2.1二叉树的概念与结构

在树形结构中，我们最常⽤的就是⼆叉树，⼀棵⼆叉树是结点的⼀个有限集合，该集合由⼀个根结点 加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。

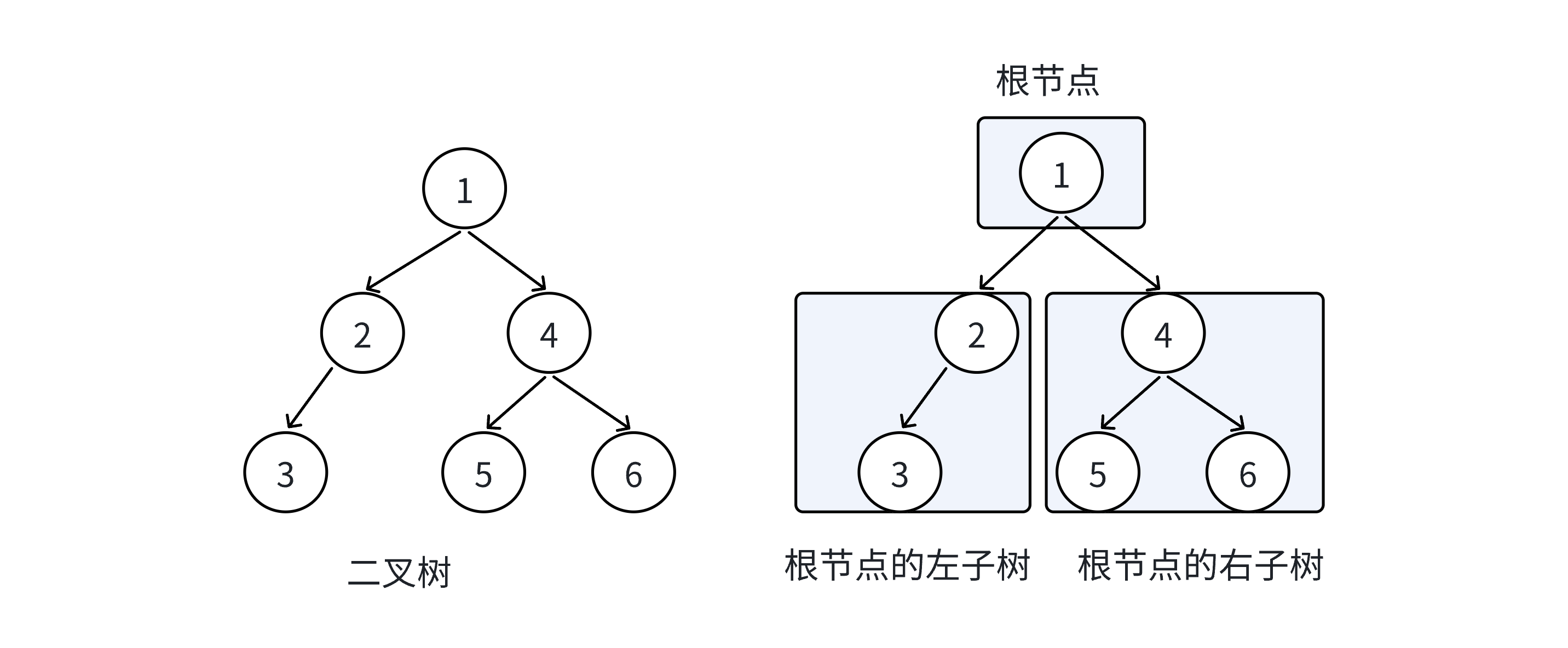
从上图可以看出⼆叉树具备以下特点：

1. ⼆叉树不存在度⼤于 2 的结点

2. ⼆叉树的⼦树有左右之分，次序不能颠倒，因此⼆叉树是有序树

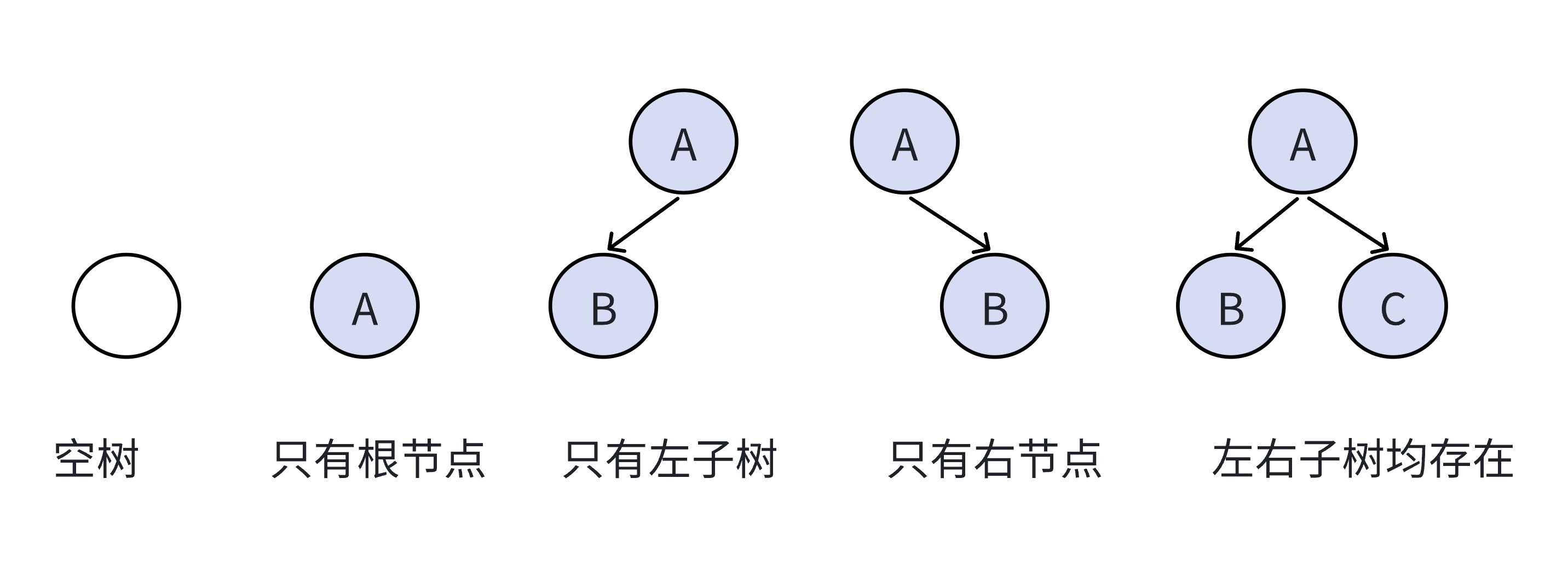
注意：对于任意的⼆叉树都是由以下⼏种情况复合⽽成的 

2.2特殊的二叉树

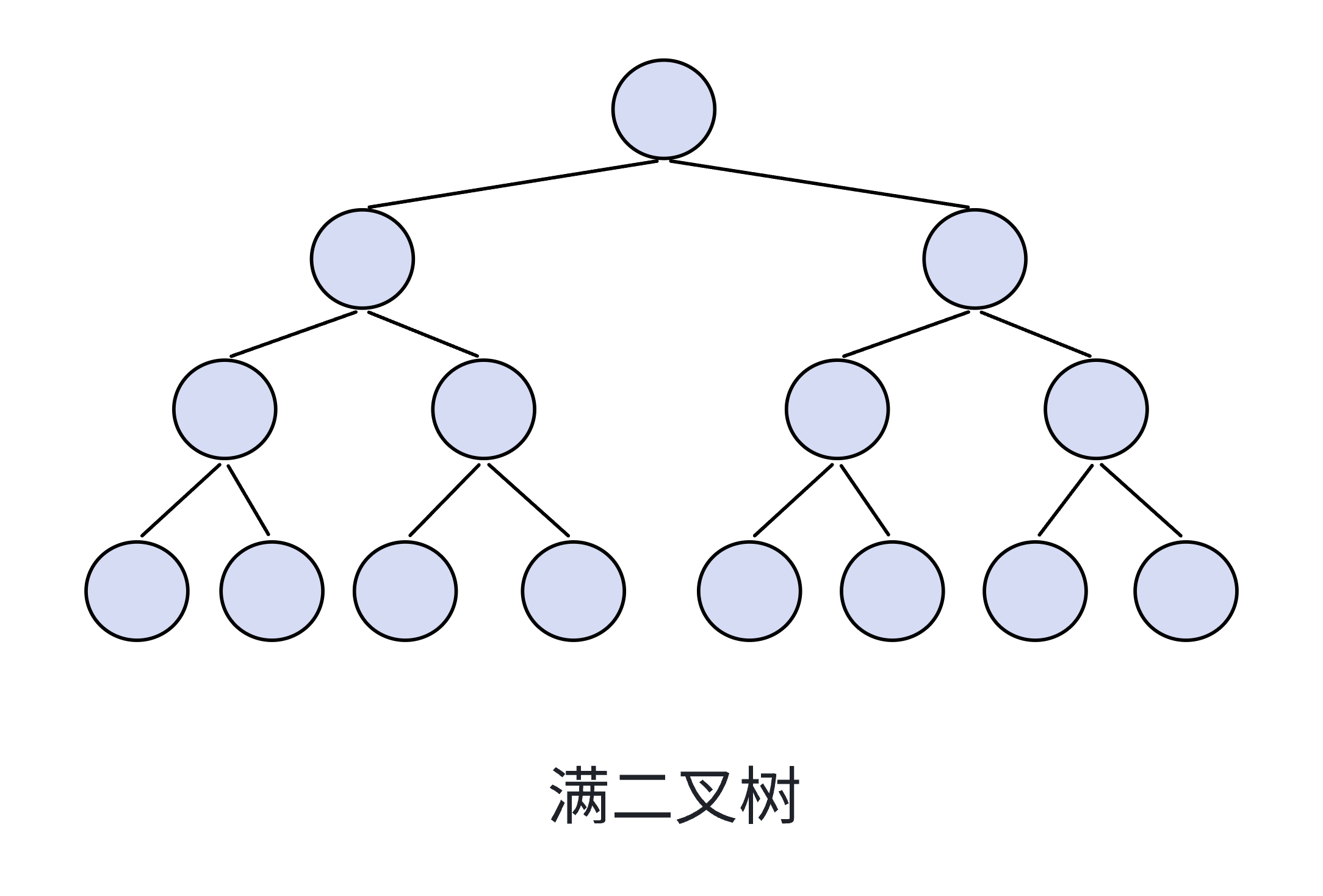
2.2.1满二叉树

⼀个⼆叉树，如果每⼀个层的结点数都达到最⼤值，则这个⼆叉树就是满⼆叉树。也就是说，如果⼀ 个⼆叉树的层数为 K ，且结点总数是2^k −1 ，则它就是满⼆叉树。

 

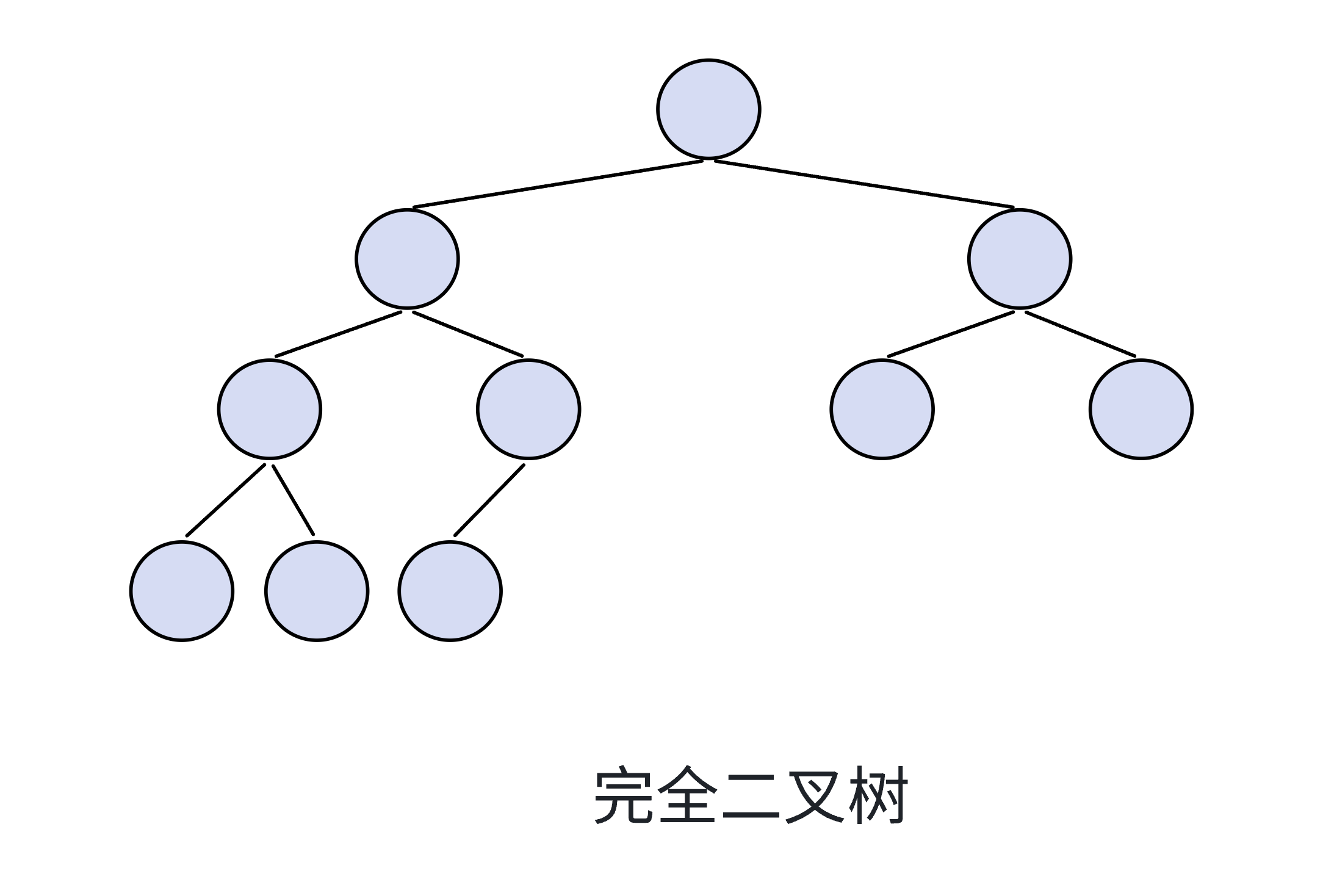
2.2.2完全二叉树 

完全⼆叉树是效率很⾼的数据结构，完全⼆叉树是由满⼆叉树⽽引出来的。

对于深度为 K 的，有 n 个 结点的⼆叉树，当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从 1 ⾄ n 的结点⼀⼀对应时称 之为完全⼆叉树。

要注意的是满⼆叉树是⼀种特殊的完全⼆叉树。

 

3.堆

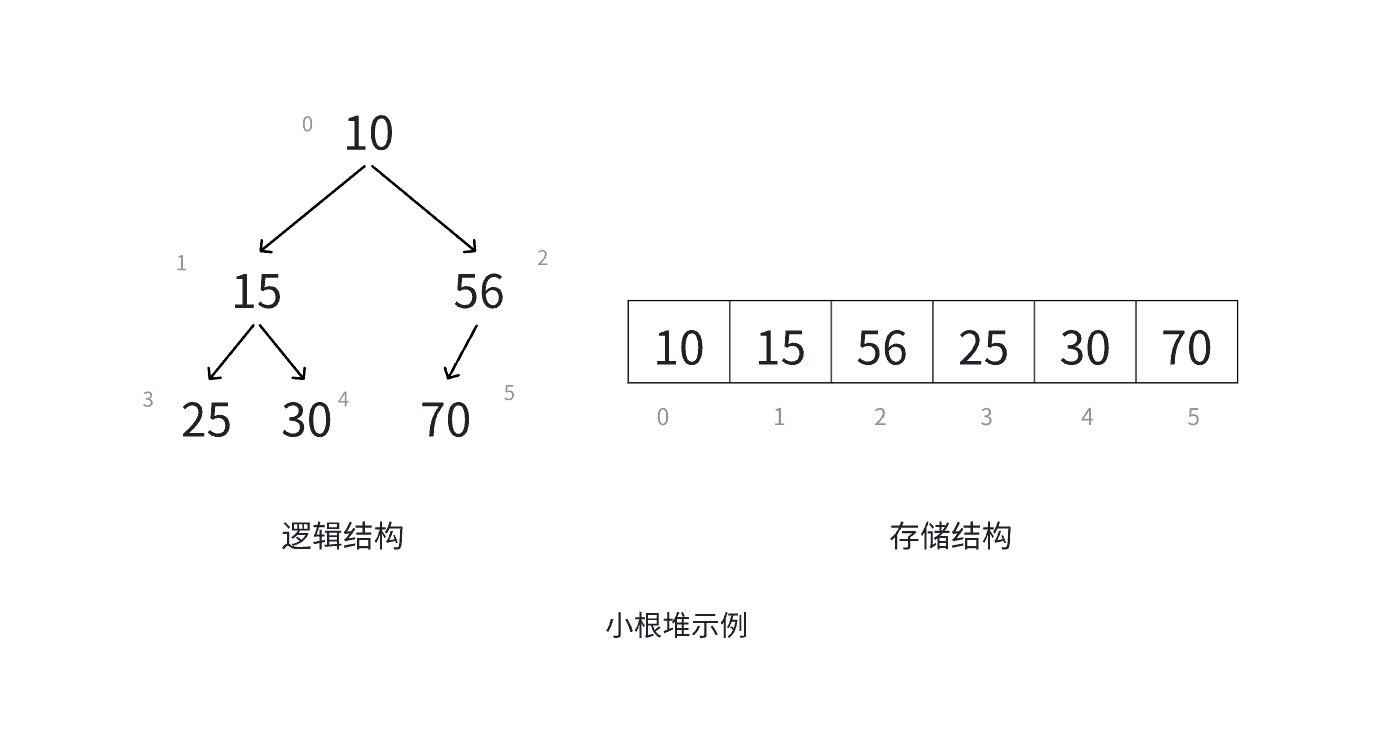
⼀般堆使⽤顺序结构的数组来存储数据，堆是⼀种特殊的⼆叉树，具有⼆叉树的特性的同时，还具备 其他的特性。

3.1堆的概念与结构

用直白点的话说就是，大数在上面就是大堆，小数在上面就是小堆

 

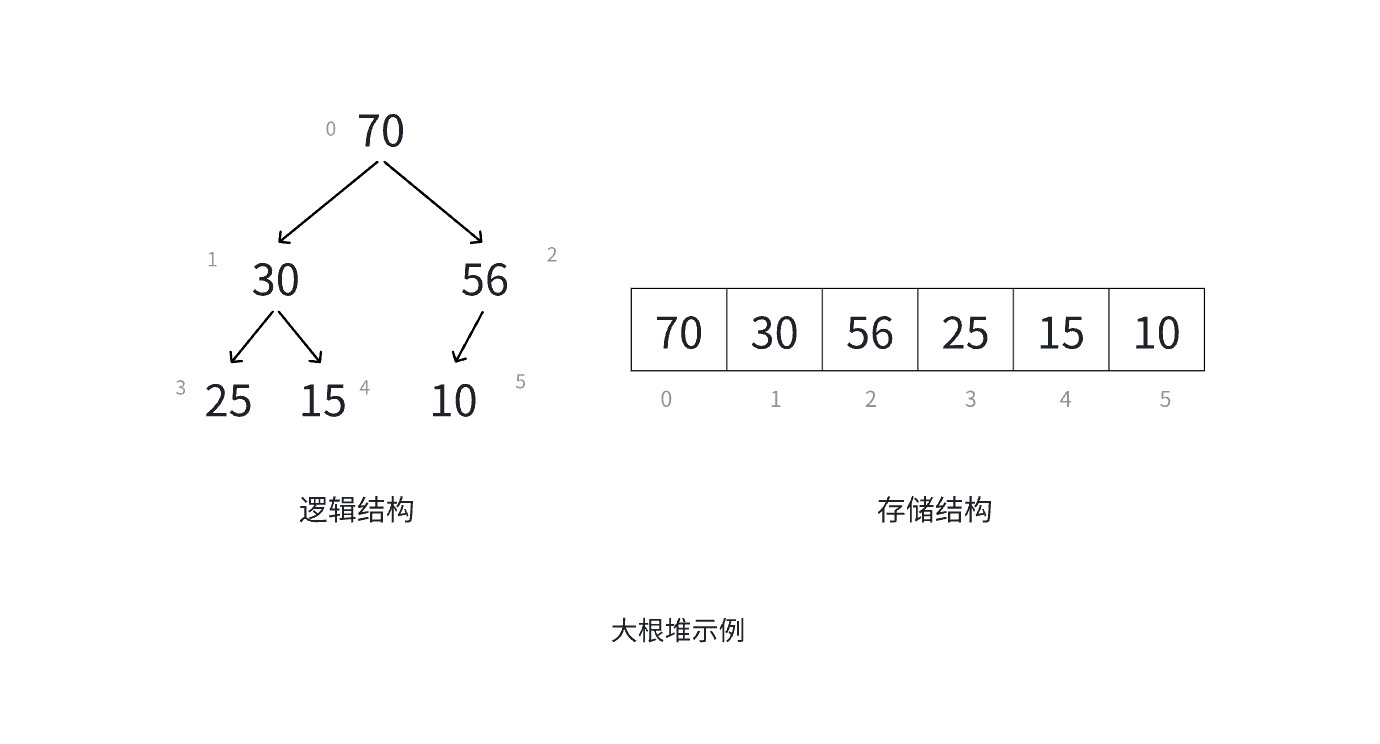
 二叉树性质

• 对于具有 n 个结点的完全⼆叉树，如果按照从上⾄下从左⾄右的数组顺序对所有结点从 0 开始编号，则对于序号为 i 的结点有：

1. 若 i>0 ， i 位置结点的双亲序号： (i-1)/2 ； i=0 ， i 为根结点编号，⽆双亲结点

2. 若 2i+1，左孩⼦序号： 2i+1 ， 2i+1>=n 否则⽆左孩⼦

3. 若 2i+2，右孩⼦序号： 2i+2 ， 2i+2>=n 否则⽆右孩⼦

3.2堆的实现

3.2.1堆的结构

以数组，类似于顺序表的方式实现

//堆的结构
typedef int HPdatatype;
typedef struct heap
{HPdatatype* arr;int size;//有效数据个数int capacity;//空间大小}HP;

3.2.2堆初始化

void HPinit(HP* php)//堆初始化
{php->arr = NULL;php->size = php->capacity = 0;
}

3.2.3向堆插入数据

如果是顺序表插入数据，直接将数据尾插即可，可是在堆内插入数据后，就要重新考虑是否要改变顺序，这里我们就采用向上调整算法

向上调整算法的核心思路就是把插入的节点和其母节点进行比较，然后改变顺序。 

 

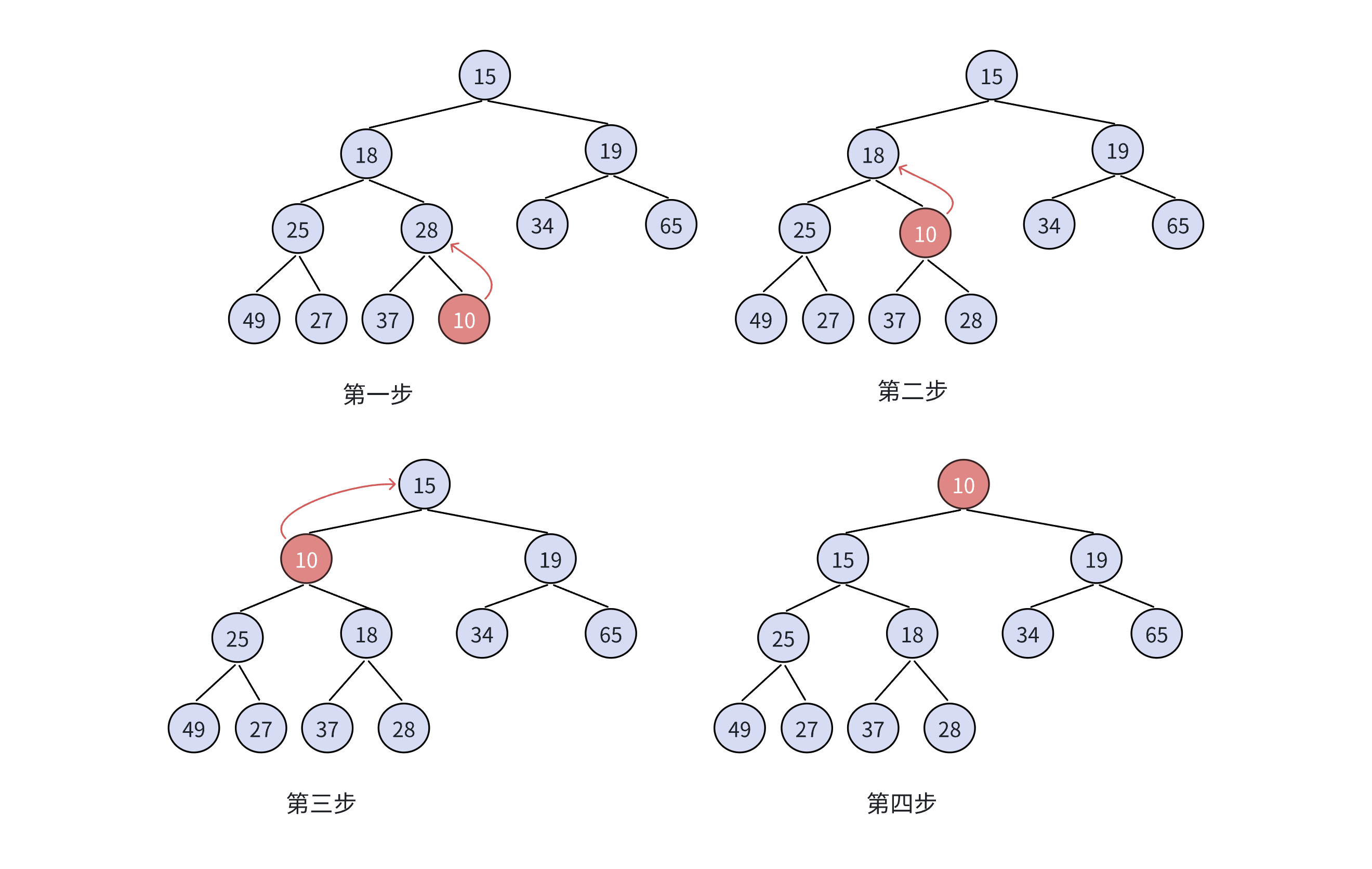
void Adjustup(HPdatatype* arr,int child)//向上调整算法
{int parrent = (child - 1) / 2;//这里的child是指他的下标，不是数据while (child > 0){if (arr[child] < arr[parrent]){//调整Swap(&arr[child], &arr[parrent]);child = parrent;parrent = (child - 1) / 2;//母节点和子节点的关系}else{break;}}
}

 

void HPpush(HP* php,HPdatatype x)//向堆插入数据
{assert(php);//判断空间是否足够if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPdatatype* tmp = (HPdatatype*)realloc(php->arr,sizeof(HPdatatype)*newcapacity);if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x;Adjustup(php->arr, php->size);php->size++;}

 3.2.4出堆

 在堆中，出堆是将堆顶的数据删除之后将整个堆重新排序。

在这里我们采用向下调整算法，所谓向下调整算法，就是将最后一个节点和和堆顶交换，然后和子节点进行比较，进行交换。

 

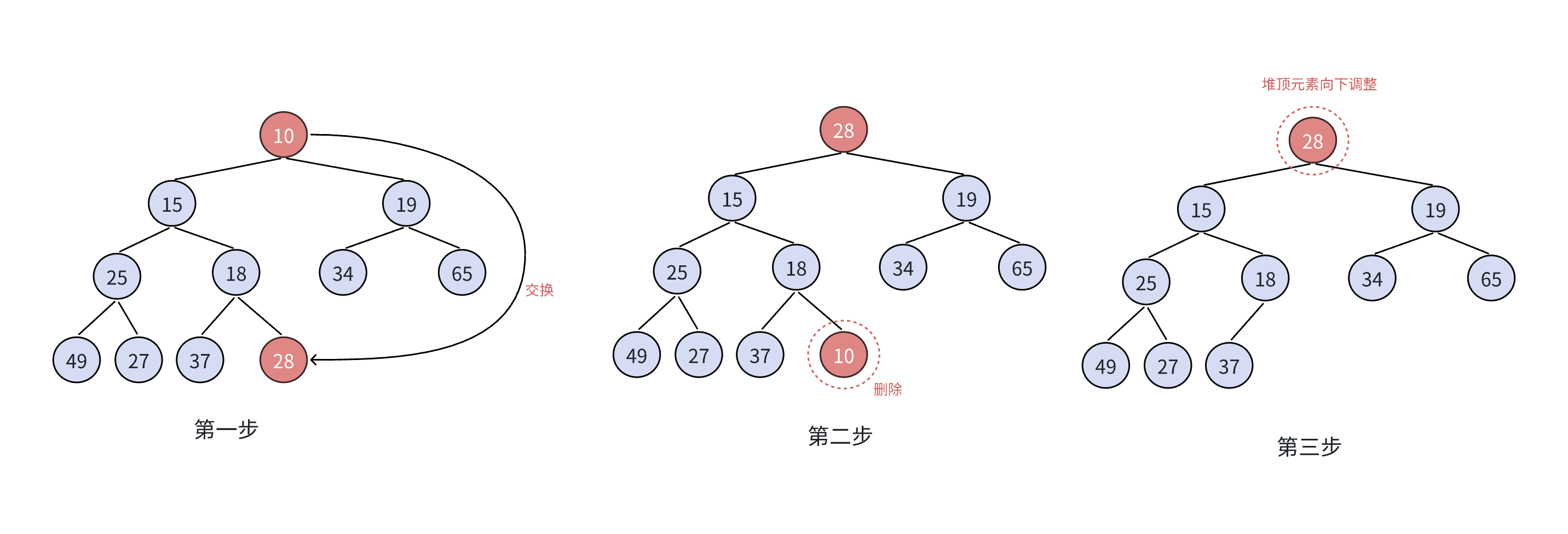
void Adjustdown(HPdatatype* arr,int parent,int n)//向下调整算法
{int child = parent * 2 + 1;//左孩子while (child < n){//小堆>if (child+1<n && arr[child]<arr[child + 1])//确保是将最小（大）的数进行交换	{child++;}//if (arr[child] > arr[parent])//小堆<{//调整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HPpop(HP* php)//出堆
{assert(!HPempty(php));//将最开始的父节点删掉Swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下调整Adjustdown(php->arr, 0, php->size);}

 3.2.5堆排序

我们根据堆的数据结构，可以较为简单的实现堆排序，如下码

void HPsort1(int* arr, int n)//堆排序
{HP hp;HPinit(&hp);for (int i = 0;i < n;i++){HPpush(&hp, arr[i]);}int i = 0;while (!HPempty(&hp)){int top = HPtop(&hp);arr[i++] = top;HPpop(&hp);}HPdestroy(&hp);
}

但是如果不借助堆的数据结构，该怎么样进行排序呢？ 

其思路就是：数组建堆，⾸尾交换，交换后的堆尾数据从堆中删掉，将堆顶数据向下调整选出次⼤的数据

void HPsort2(int* arr, int n)//堆排序
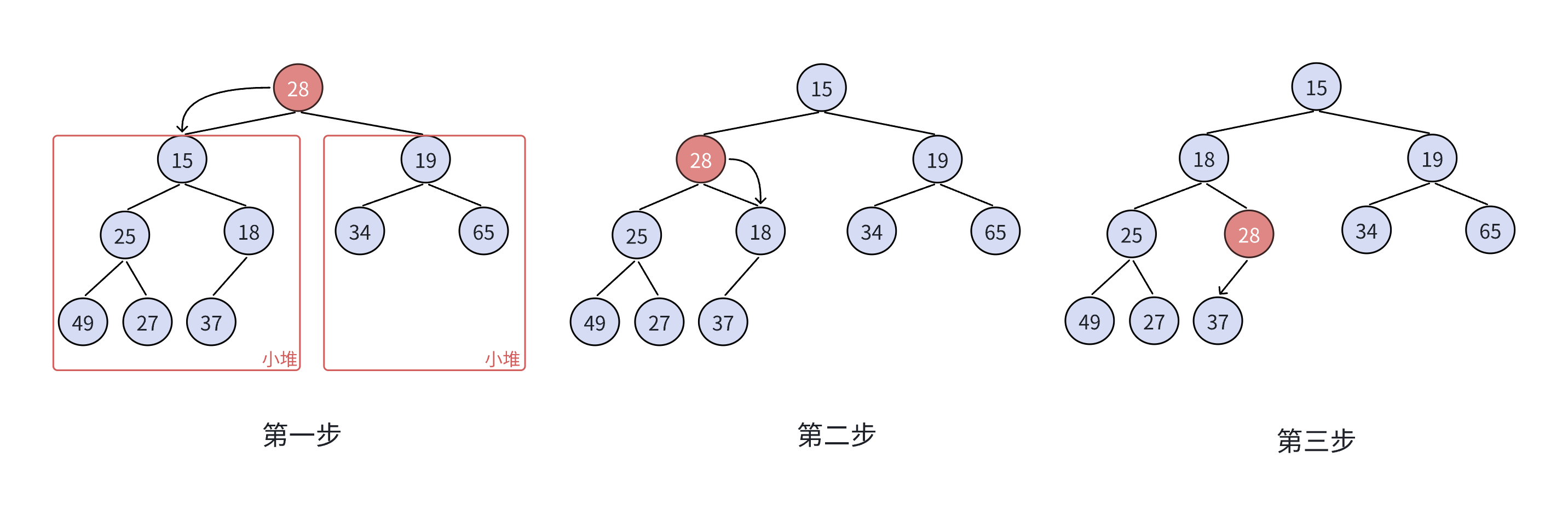
{//根据数组建堆，向下调整建堆for (int i = (n - 1 - 1) / 2;i > 0;i--)//下标是n-1，父节点是n-1/2{Adjustdown(arr, i, n);}//根据堆进行排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);Adjustdown(arr, 0, end);end--;}}

 其中建堆过程如下

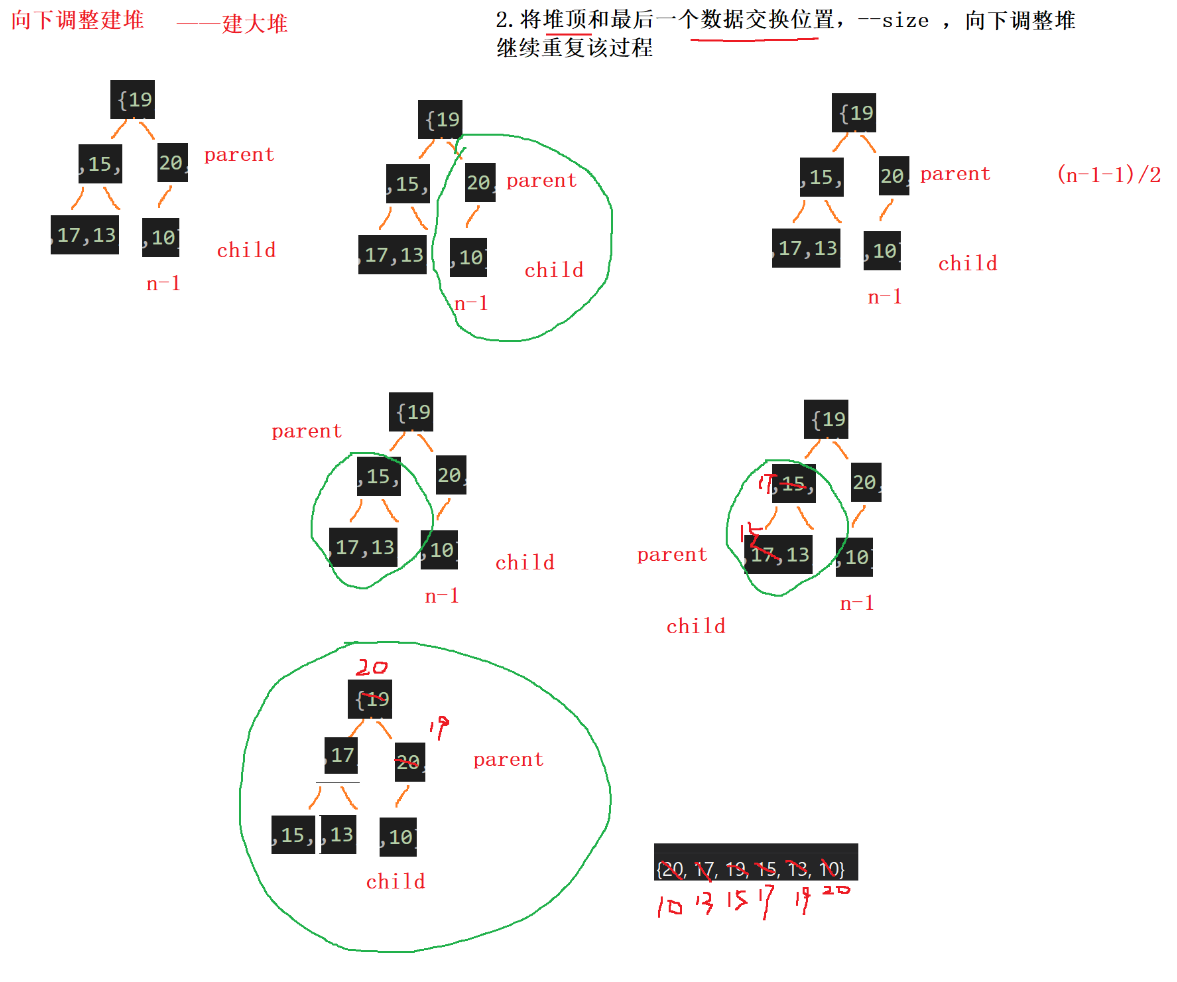
先调整最右子数，再调整相邻的子树。，再调整整个树

然后排序过程的原理就是

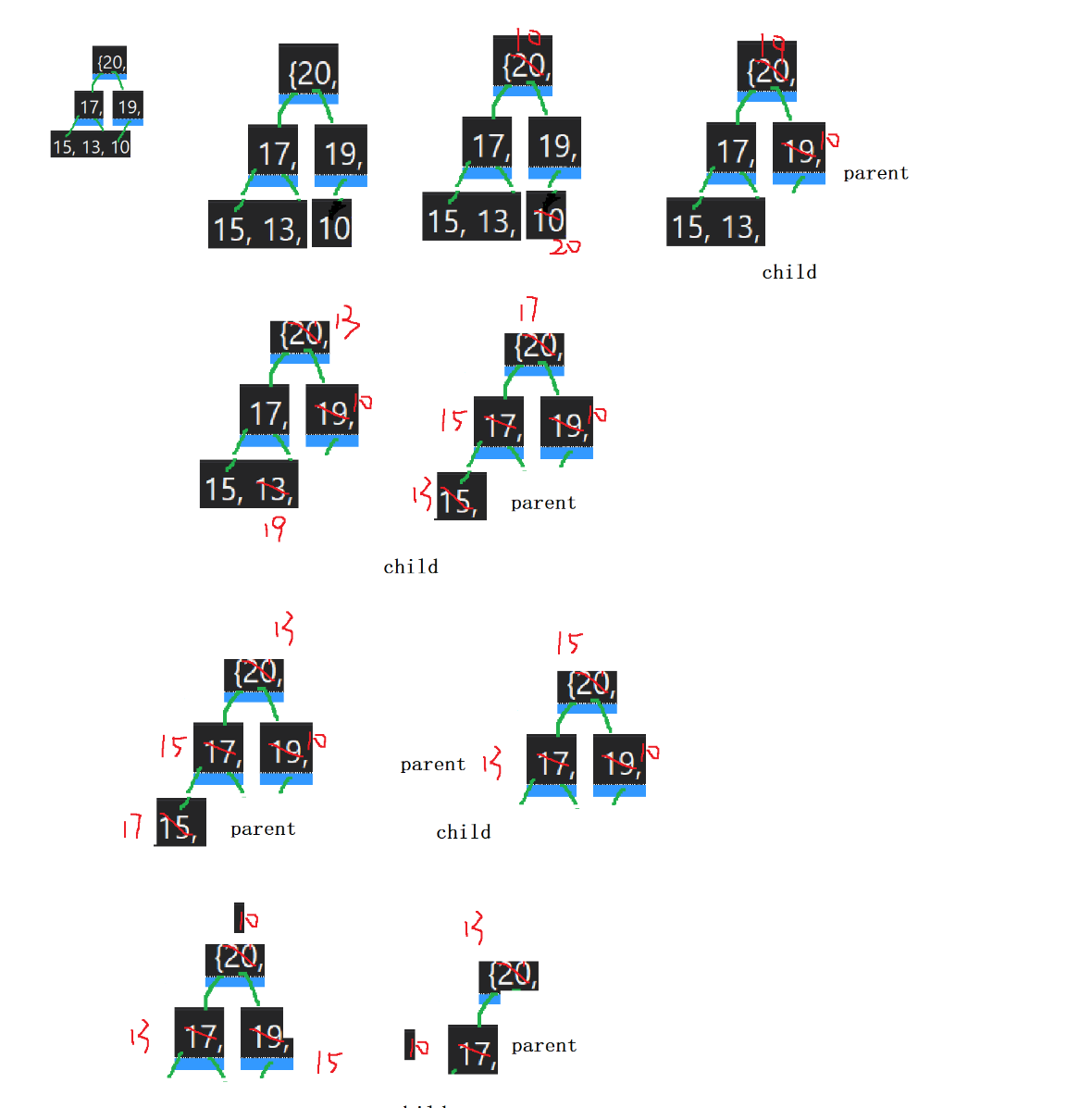
 将最大和最小的数交换位置，即将最大数储存在数组末端，然后在进行向下调整，此次调整时，将数组的下标自减，就可以最后一个数排除在外，然后重复这个过程，就可以实现排序

3.3完整代码实现

.h文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//堆的结构
typedef int HPdatatype;
typedef struct heap
{HPdatatype* arr;int size;//有效数据个数int capacity;//空间大小}HP;void HPinit(HP* php);//堆初始化
void HPdestroy(HP* php);//销毁堆
void HPpush(HP* php,HPdatatype x);//向堆插入数据
void Adjustup(HPdatatype* arr, int child);//向上调整算法
void Adjustdown(HPdatatype* arr,int parent,int n);//向下调整算法
void Swap(int* x, int* y);//交换函数
void HPprint(HP* php);//打印函数
void HPpop(HP* php);//出堆
bool HPempty(HP* php);//判空
HPdatatype HPtop(HP* php);//取堆顶数据
void HPsort1(int* arr, int n);//堆排序--数据结构
void HPsort2(int* arr, int n);//堆排序

.c文件 

#define _CRT_SECURE_NO_WARNINGS
#include"heap.h"void HPinit(HP* php)//堆初始化
{php->arr = NULL;php->size = php->capacity = 0;
}
void HPdestroy(HP* php)//销毁堆
{if (php->arr){free(php->arr);php->arr = NULL;php->size = php->capacity = 0;}
}
void Swap(int* x, int* y)//交换函数
{int tmp = *x;*x = *y;*y = tmp;
}
void Adjustup(HPdatatype* arr,int child)//向上调整算法
{int parrent = (child - 1) / 2;while (child > 0){//小堆<//大堆>if (arr[child] < arr[parrent]){//调整Swap(&arr[child], &arr[parrent]);child = parrent;parrent = (child - 1) / 2;}else{break;}}
}
void HPpush(HP* php,HPdatatype x)//向堆插入数据
{assert(php);//判断空间是否足够if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPdatatype* tmp = (HPdatatype*)realloc(php->arr,sizeof(HPdatatype)*newcapacity);if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x;Adjustup(php->arr, php->size);php->size++;}
void HPprint(HP* php)//打印函数
{for (int i = 0;i < php->size;i++){printf("%d ",php->arr[i]);}printf("\n");
}
bool HPempty(HP* php)//判空
{assert(php);return php->size == 0;
}
void Adjustdown(HPdatatype* arr,int parent,int n)//向下调整算法
{int child = parent * 2 + 1;//左孩子while (child < n){if (child+1<n && arr[child]> arr[child + 1])//小堆>{child++;}//if (arr[child] < arr[parent])//小堆<{//调整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HPpop(HP* php)//出堆
{assert(!HPempty(php));//将最开始的父节点删掉Swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下调整Adjustdown(php->arr, 0, php->size);}
HPdatatype HPtop(HP* php)//取堆顶数据
{assert(!HPempty(php));return php->arr[0];
}
void HPsort1(int* arr, int n)//堆排序
{HP hp;HPinit(&hp);for (int i = 0;i < n;i++){HPpush(&hp, arr[i]);}int i = 0;while (!HPempty(&hp)){int top = HPtop(&hp);arr[i++] = top;HPpop(&hp);}HPdestroy(&hp);
}

 .c文件（测试）

#define _CRT_SECURE_NO_WARNINGS
#include"heap.h"void HPsort2(int* arr, int n)//堆排序
{//根据数组建堆，向下调整建堆for (int i = (n - 1 - 1) / 2;i >= 0;i--){Adjustdown(arr, i, n);}//根据堆进行排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);Adjustdown(arr, 0, end);end--;}}void test01()
{HP hp;HPinit(&hp);HPpush(&hp, 56);HPpush(&hp, 15);HPpush(&hp, 10);HPpop(&hp);HPprint(&hp);HPdestroy(&hp);
}
test02()
{HP hp;HPinit(&hp);HPpush(&hp, 66);HPpush(&hp, 26);HPpush(&hp, 76);HPprint(&hp);printf("\n");while (!HPempty(&hp)){int top = HPtop(&hp);printf("%d ", top);HPpop(&hp);}HPdestroy(&hp);}
int main()
{//test01();/*test02();*/int arr[6] = { 19, 23, 45, 43, 22, 11 };/*HPsort1(arr, 6);*/HPsort2(arr, 6);for (int i = 0;i < 6;i++){printf("%d ", arr[i]);}return 0;
}

本次分享就到这里结束了，后续会继续更新，感谢阅读！

 

 

 

 

 

 

 

http://www.xdnf.cn/news/7111.html

相关文章：

  • BUUCTF——ReadlezPHP
  • KnowCard：我的知识卡片生成器是怎么炼成的？
  • 高能数造闪耀 CIBF 2025，以创新技术引领新能源智造新征程
  • Android 自定义悬浮拖动吸附按钮
  • MyBatis 延迟加载与缓存
  • 【时时三省】(C语言基础)数组习题
  • Linux虚拟文件系统(1)
  • 《沙尘暴》观影记：当家庭成为人性的修罗场
  • 记录一次修改nacos安全问题导致服务调用出现404
  • 【Canvas与诗词】醉里挑灯看剑 梦回吹角连营
  • DeepSeek 赋能脑科学：解锁神经科学研究与应用的新密码
  • 一文讲解Function Calling是什么？
  • vmware虚拟机运行多个产生卡顿问题
  • python打卡第29天
  • Python——一些琐碎知识点
  • Java八股文——Java基础篇
  • 刷题心得：荷兰国旗问题与三指针法题目背景
  • AM32电调学习解读七：其他代码文件介绍
  • 2901. 最长相邻不相等子序列 II
  • Seata源码—6.Seata AT模式的数据源代理一
  • 2025.05.17得物机考笔试真题第二题
  • React 19中useContext不需要Provider了。
  • Java基础知识总结（超详细整理）
  • 32LED心形灯程序源代码
  • 常见的 HTTP 接口（请求方法）
  • PCB设计（十九）PCB设计中NPN/PNP选型策略
  • Window远程连接Linux桌面版
  • 掘金欧洲宠物经济新蓝海：比利时天然宠粮市场爆发与跨境新机遇
  • c++从入门到精通（六）--特殊工具与技术-完结篇
  • Azure 机器学习初学者指南