Transformer KV缓存优化(MHA、MQA、GQA、MLA,参考:DeepSeek-V2)
这里写目录标题
- 1、说明
- 2、KV缓存优化
- 2.0 KV缓存(Cache)的核心原理
- 2.1 KV缓存优化
- 2.2 性能对比
- 2.3 架构
- 2.4多头注意力 (MHA)
- 2.5 多头潜在注意力 (MLA)
- 2.5.1 低秩键值联合压缩 (Low-Rank Key-Value )
- 2.5.2. 解耦旋转位置嵌入(Dcoupled RoPE )
- 一、核心问题:传统RoPE与低秩KV压缩的冲突
- 二、解耦RoPE策略:分离位置信息的“双重表示”
- 三、关键公式与实例解析
- 1. **符号定义(简化维度示例)**
- 2. **位置相关查询 q t R q_t^R qtR 的生成(公式14)**
- 3. **共享位置键 k t R k_t^R ktR 的生成(公式15)**
- 4. **查询与键的拼接(公式16-17)**
- 5. **注意力计算(公式18)**
- 四、核心优势:通过“分离-拼接”实现高效与位置建模的双赢
- 五、与传统RoPE的对比(以1头为例)
- 六、总结:解耦策略如何让MLA“两全其美”
- 2.5.3.MLA完整计算过程
- 数学:矩阵分块计算,多token的矩阵分成单个token相乘
- 向量与多维矩阵乘法
- 矩阵分块计算
- 多Token矩阵分块处理
- 分块计算的优势
- 总结
1、说明
本文参考: 论文DeepSeek-V2
我们用我们提出的多头潜在注意力 (MLA) 和 DeepSeekMoE 优化了 Transformer 框架(Vaswani et al., 2017)中的注意力模块和前馈网络 (FFN)。(1) 在注意力机制的背景下,多头注意力 (MHA) 的键值 (KV) 缓存(Vaswani et al., 2017)对 LLM 的推理效率构成了重大障碍。已经探索了各种方法来解决这个问题,包括分组查询注意力 (GQA) (Ainslie et al., 2023) 和多查询注意力 (MQA) (Shazeer, 2019)。但是,这些方法在尝试减少 KV 缓存时通常会牺牲性能。为了实现两全其美的效果,我们引入了 MLA,这是一种配备了低秩键值联合压缩的注意力机制。从经验上讲,MLA 实现了优于 MHA 的性能,同时显著降低了推理过程中的 KV 缓存,从而提高了推理效率。(2) 对于前馈网络 (FFN),我们遵循 DeepSeekMoE 架构 (Dai et al., 2024),该架构采用细粒度的专家分割和共享的专家隔离,以提高专家专业化的潜力。与 GShard 等传统 MoE 架构相比,DeepSeekMoE 架构表现出巨大的优势(Lepikhin et al., 2021),使我们能够以经济的成本训练强大的模型。由于我们在训练期间采用专家并行性,因此我们还设计了补充机制来控制通信开销并确保负载平衡。通过结合这两种技术,DeepSeek-V2 同时具有强大的性能(图 1(a))、经济的训练成本和高效的推理吞吐量(图 1(b))。
2、KV缓存优化
2.0 KV缓存(Cache)的核心原理
Transformer 的 KV Cache(Key-Value Cache) 是一种针对自回归生成任务(如文本生成)的推理优化技术,通过缓存中间计算结果减少重复运算,显著提升模型效率。以下从原理、作用、实现等角度详细解析:
一、KV Cache 的核心原理
-
自注意力机制的计算冗余问题
在 Transformer 的自注意力机制中,每个 token 需计算对应的 Query(Q)、Key(K)、Value(V)矩阵。生成新 token 时,若未缓存 K 和 V,模型需重新计算所有历史 token 的 K 和 V,导致计算复杂度为 O(n²)(n 为序列长度)。 -
KV Cache 的缓存机制
• 首次推理:处理初始 token 时,完整计算并存储 K 和 V 矩阵。
• 后续推理:生成新 token 时,仅计算当前 token 的 Q,并从缓存中读取历史 K 和 V,避免重复计算。复杂度降至 O(n)。
• 动态更新:将新 token 的 K 和 V 追加至缓存,供后续步骤复用。
-
传统Transformer的缺陷
在自注意力机制中,每个token的输出依赖于对所有历史token的注意力计算:- 查询(Query, Q)、键(Key, K)、值(Value, V) 由输入通过线性层生成:
Q = X W Q , K = X W K , V = X W V Q = XW_Q, \quad K = XW_K, \quad V = XW_V Q=XWQ,K=XWK,V=XWV - 注意力分数计算为:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dkQKT)V
在生成任务(如逐个token生成文本)中,若每次生成新token都重新计算所有历史token的K和V,会导致计算量随序列长度呈平方增长(时间复杂度为 O ( n 2 ) O(n^2) O(n2)),效率极低。
- 查询(Query, Q)、键(Key, K)、值(Value, V) 由输入通过线性层生成:
-
KV缓存的核心思想
缓存历史层的K和V,避免重复计算:
在推理阶段(生成任务),当处理第 i i i 个token时,仅计算当前token的Q,而K和V则复用之前 i − 1 i-1 i−1 个token的缓存结果。具体步骤如下:- 首次计算:处理第1个token时,生成其K₁和V₁,存入缓存。
- 后续生成:处理第 n n n 个token时:
- 计算当前token的Qₙ。
- 从缓存中获取前 n − 1 n-1 n−1 个token的K₁₋ₙ₋₁和V₁₋ₙ₋₁,与当前Kₙ、Vₙ拼接后,用于计算注意力。
- 将新的Kₙ和Vₙ添加到缓存中,供下一个token使用。
通过这种方式,每次生成新token的时间复杂度降至 O ( n ) O(n) O(n)(仅新增一次线性计算和拼接操作),大幅提升长序列生成效率。
二、KV Cache 的适用场景与限制
- 适用场景
• 自回归模型:如 GPT、LLaMA 等生成式模型。
• 实时交互任务:聊天机器人、翻译等对延迟敏感的场景。
- 限制
• 因果性要求:仅适用于因果掩码(Causal Mask)模型,如 Decoder-only 架构。
• 显存瓶颈:长序列生成时缓存占用显存,需权衡速度与内存。
三、KV Cache 的核心作用
- 加速推理
• 通过避免重复计算 K 和 V,推理速度提升 2-3 倍。例如,某聊天机器人的响应时间从 0.5 秒降至 0.2 秒。
• 实验表明,开启 KV Cache 后,生成 1000 个 token 的耗时从指数级增长(如 332 秒)变为线性增长(29 秒)。
- 降低显存占用
• 复用缓存减少中间张量的存储需求。例如,某移动设备上的内存占用从 1GB 降至 0.6GB。
• 尽管缓存占用显存(如 Llama3-70B 在 4k token 时需约 10.5GB),但整体效率仍显著优化。
- 支持长序列生成
• 长文本生成时,KV Cache 维持对历史上下文的完整理解,确保语义连贯性。
2.1 KV缓存优化
我们用我们提出的多头潜在注意力 (MLA) 和 DeepSeekMoE 优化了 Transformer 框架(Vaswani et al., 2017)中的注意力模块和前馈网络 (FFN)。(1) 在注意力机制的背景下,多头注意力 (MHA) 的键值 (KV) 缓存(Vaswani et al., 2017)对 LLM 的推理效率构成了重大障碍。已经探索了各种方法来解决这个问题,包括分组查询注意力 (GQA) (Ainslie et al., 2023) 和多查询注意力 (MQA) (Shazeer, 2019)。但是,这些方法在尝试减少 KV 缓存时通常会牺牲性能。为了实现两全其美的效果,我们引入了 MLA,这是一种配备了低秩键值联合压缩的注意力机制。从经验上讲,MLA 实现了优于 MHA 的性能,同时显著降低了推理过程中的 KV 缓存,从而提高了推理效率。(2) 对于前馈网络 (FFN),我们遵循 DeepSeekMoE 架构 (Dai et al., 2024),该架构采用细粒度的专家分割和共享的专家隔离,以提高专家专业化的潜力。与 GShard 等传统 MoE 架构相比,DeepSeekMoE 架构表现出巨大的优势(Lepikhin et al., 2021),使我们能够以经济的成本训练强大的模型。由于我们在训练期间采用专家并行性,因此我们还设计了补充机制来控制通信开销并确保负载平衡。通过结合这两种技术,DeepSeek-V2 同时具有强大的性能(图 1(a))、经济的训练成本和高效的推理吞吐量(图 1(b))。
2.2 性能对比
2.1 多头潜在注意力:提升推理效率
传统Transformer模型通常采用多头注意力(MHA,Vaswani等人,2017),但在生成过程中,其庞大的键值(KV)缓存会成为限制推理效率的瓶颈。为减少KV缓存,研究者提出了多查询注意力(MQA,Shazeer,2019)和分组查询注意力(GQA,Ainslie等人,2023)。这些方法需要的KV缓存规模较小,但性能不及MHA(附录D.1提供了MHA、GQA和MQA的消融实验结果)。
针对DeepSeek-V2,我们设计了一种创新的注意力机制——多头潜在注意力(MLA)。通过低秩键值联合压缩,MLA在实现比MHA更强性能的同时,仅需显著更少的KV缓存。以下将介绍其架构,并在附录D.2中提供MLA与MHA的对比。
我们在表 1 中演示了不同注意力机制之间每个令牌的 KV 缓存的比较。MLA 只需要少量的 KV 缓存,相当于只有 2.25 组的 GQA,但可以达到比 MHA 更强的性能。

表 1 不同注意力机制之间每个令牌的 KV 缓存比较。 n h n_{h} nh 表示关注头的数量, d h d_{h} dh 表示每个关注头的维度,l 表示层数, n g n_{g} ng 表示 GQA 中的组数, d c d_{c} dc 和 d h R d_{h}^{R} dhR 分别表示 MLA 中解耦查询和 key 的 KV 压缩维度和每头维度。KV 缓存量由元素数量来衡量,与存储精度无关。对于 DeepSeek-V2, d c d_{c} dc 设置为 4 d h 4 d_{h} 4dh, d h R d_{h}^{R} dhR 设置为 d h 2 \frac{d_{h}}{2} 2dh。因此,它的 KV 缓存等于只有 2.25 组的 GQA,但其性能比 MHA 强。
2.3 架构
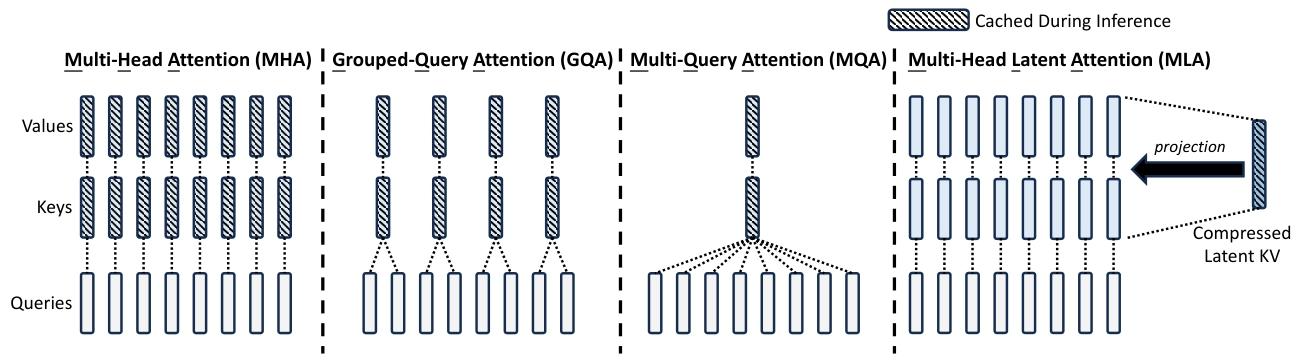

图 3 |多头注意力 (MHA)、分组查询注意力 (GQA)、多查询注意力 (MQA) 和多头潜在注意力 (MLA) 的简化图示。MLA 通过将 key 和 values 联合压缩成一个 latent vector,显著降低了推理过程中的 KV 缓存。
2.4多头注意力 (MHA)
预备知识:标准多头注意力
首先介绍标准MHA机制作为背景。设d为嵌入维度, n h n_{h} nh为注意力头数, d h d_{h} dh为每头维度, h t ∈ R d h_{t} \in \mathbb{R}^{d} ht∈Rd为第t个token在注意力层的输入。标准MHA通过三个矩阵WQ、WK、 W V ∈ R d h n h × d W^{V} \in \mathbb{R}^{d_{h} n_{h} ×d} WV∈Rdhnh×d分别生成qt、kt、 v t ∈ R d h n h v_{t} \in \mathbb{R}^{d_{h} n_{h}} vt∈Rdhnh :
n h n_{h} nh be the number of attention heads, d h d_{h} dh be the dimension
per head, and h t ∈ R d h_{t} \in \mathbb{R}^{d} ht∈Rdbe the attention input of the
𝑡-th token at an attention layer. Standard MHA first produces q t q_{t} qt
,kt, v t ∈ R d h n h v_{t} \in \mathbb{R}^{d_{h} n_{h}} vt∈Rdhnh through three matrices
w Q w^{Q} wQ , W K W^{K} WK , W V ∈ R d h n h × d W^{V} \in \mathbb{R}^{d_{h} n_{h} ×d} WV∈Rdhnh×d ,
respectively:
q t = W Q h t , ( 1 ) q_{t}=W^{Q} h_{t}, \quad(1) qt=WQht,(1)
k t = W K h t , ( 2 ) k_{t}=W^{K} h_{t}, (2) kt=WKht,(2)
v t = W V h t , ( 3 ) v_{t}=W^{V} h_{t}, (3) vt=WVht,(3)
随后,qt、kt、vt被切分为nh个头以进行多头注意力计算:
[ q t , 1 ; q t , 2 ; … ; q t , n h ] = q t , ( 4 ) [q_{t,1}; q_{t,2}; \dots; q_{t,n_h}] = q_t, \quad (4) [qt,1;qt,2;…;qt,nh]=qt,(4)
[ k t , 1 ; k t , 2 ; … ; k t , n h ] = k t , ( 5 ) [k_{t,1}; k_{t,2}; \dots; k_{t,n_h}] = k_t, \quad (5) [kt,1;kt,2;…;kt,nh]=kt,(5)
[ v t , 1 ; v t , 2 ; … ; v t , n h ] = v t , ( 6 ) [v_{t,1}; v_{t,2}; \dots; v_{t,n_h}] = v_t, \quad (6) [vt,1;vt,2;…;vt,nh]=vt,(6)
o t , i = ∑ j = 1 t Softmax j ( q t , i T k j , i d h ) v j , i , ( 7 ) o_{t,i} = \sum_{j=1}^t \text{Softmax}_j \left( \frac{q_{t,i}^T k_{j,i}}{\sqrt{d_h}} \right) v_{j,i}, \quad (7) ot,i=j=1∑tSoftmaxj(dhqt,iTkj,i)vj,i,(7)
u t = W O [ o t , 1 ; o t , 2 ; … ; o t , n h ] , ( 8 ) u_t = W^O [o_{t,1}; o_{t,2}; \dots; o_{t,n_h}], \quad (8) ut=WO[ot,1;ot,2;…;ot,nh],(8)
其中q𝑡,𝑖, k𝑡,𝑖, v t , i ∈ R d k v_{t, i} \in \mathbb{R}^{d_{k}} vt,i∈Rdk分别表示第 i 个注意力头的查询、键和值; W O ∈ R d × d h n h W^{O} \in \mathbb{R}^{d ×d_{h} n_{h}} WO∈Rd×dhnh 为输出投影矩阵。推理时,所有键和值需缓存以加速计算,因此MHA每个token需缓存 2 n h d h l 2 n_{h} d_{h} l 2nhdhl个元素( l l l 表示层数)。在模型部署中,这种庞大的KV缓存是限制最大批量大小和序列长度的主要瓶颈。
注意: KV,不是超参数 W K W^{K} WK , W V ∈ R d h n h × d W^{V} \in \mathbb{R}^{d_{h} n_{h} ×d} WV∈Rdhnh×d ,而是相乘后的KV矩阵: k t = W K h t , ( 2 ) 、 v t = W V h t , ( 3 ) k_{t}=W^{K} h_{t}, (2)、v_{t}=W^{V} h_{t},(3) kt=WKht,(2)、vt=WVht,(3)
where q𝑡,𝑖, k𝑡,𝑖, v t , i ∈ R d k v_{t, i} \in \mathbb{R}^{d_{k}} vt,i∈Rdk denote the
query, key, and value of the 𝑖-th attention head, respectively;
W O ∈ R d × d h n h W^{O} \in \mathbb{R}^{d ×d_{h} n_{h}} WO∈Rd×dhnh denotes the output projection matrix. During inference, all keys and values need,
to be cached to accelerate inference, so MHA needs to cache 2 n h d h l 2 n_{h} d_{h} l 2nhdhl elements for each token. In model deployment, this heavy KV cache is a large bottleneck that limits the maximum batch size and sequence length.
2.5 多头潜在注意力 (MLA)
2.5.1 低秩键值联合压缩 (Low-Rank Key-Value )
MLA的核心是通过键值的低秩联合压缩来减少KV缓存:
c t K V = W D K V h t , ( 9 ) c_t^{KV} = W^{DKV} h_t, \quad (9) ctKV=WDKVht,(9)
k t C = W U K c t K V , ( 10 ) k_t^C = W^{UK} c_t^{KV}, \quad (10) ktC=WUKctKV,(10)
v t C = W U V c t K V , ( 11 ) v_t^C = W^{UV} c_t^{KV}, \quad (11) vtC=WUVctKV,(11)
其中, c t K V ∈ R d c c_t^{KV} \in \mathbb{R}^{d_c} ctKV∈Rdc 是键和值的压缩潜向量; d c ( ≪ d h n h ) d_c \ (\ll d_h n_h) dc (≪dhnh) 表示KV压缩维度; W D K V ∈ R d c × d W^{DKV} \in \mathbb{R}^{d_c \times d} WDKV∈Rdc×d 是下投影矩阵; W U K 、 W U V ∈ R d h n h × d c W^{UK}、W^{UV} \in \mathbb{R}^{d_h n_h \times d_c} WUK、WUV∈Rdhnh×dc 分别是键和值的上投影矩阵。推理时,MLA仅需缓存 c t K V c_t^{KV} ctKV,因此其KV缓存仅包含 d c l d_c l dcl 个元素( l l l 表示层数)。此外,由于推理时 W U K W^{UK} WUK 可融入 W Q W^Q WQ, W U V W^{UV} WUV 可融入 W O W^O WO,我们甚至无需显式计算注意力的键和值。图3直观展示了MLA通过键值联合压缩减少KV缓存的过程。
为减少训练时的激活内存,我们还对查询进行低秩压缩(尽管这不会减少KV缓存):
c t Q = W D Q h t , ( 12 ) c_t^Q = W^{DQ} h_t, \quad (12) ctQ=WDQht,(12)
q t C = W U Q c t Q , ( 13 ) q_t^C = W^{UQ} c_t^Q, \quad (13) qtC=WUQctQ,(13)
其中, c t Q ∈ R d c ′ c_t^Q \in \mathbb{R}^{d'_c} ctQ∈Rdc′ 是查询的压缩潜向量; d c ′ ( ≪ d h n h ) d'_c \ (\ll d_h n_h) dc′ (≪dhnh) 表示查询压缩维度; W D Q ∈ R d c ′ × d 、 W U Q ∈ R d h n h × d c ′ W^{DQ} \in \mathbb{R}^{d'_c \times d}、W^{UQ} \in \mathbb{R}^{d_h n_h \times d'_c} WDQ∈Rdc′×d、WUQ∈Rdhnh×dc′ 分别是查询的下投影和上投影矩阵。
解释:“ W U K W^{UK} WUK 可融入 W Q W^Q WQ, W U V W^{UV} WUV 可融入 W O W^O WO”
在MLA的低秩键值联合压缩中,“ W U K W^{UK} WUK 可融入 W Q W^Q WQ, W U V W^{UV} WUV 可融入 W O W^O WO”是指通过矩阵运算的结合律,将键/值的上投影矩阵与注意力模块的输入/输出投影矩阵合并,从而在推理时跳过显式计算键和值的步骤。以下结合公式和实例具体解释:
-
矩阵吸收的数学原理
假设:- W Q W^Q WQ 是标准MHA中生成查询的投影矩阵,形状为 R d h n h × d \mathbb{R}^{d_h n_h \times d} Rdhnh×d
- W U K W^{UK} WUK 是键的上投影矩阵,形状为 R d h n h × d c \mathbb{R}^{d_h n_h \times d_c} Rdhnh×dc
- W D K V W^{DKV} WDKV 是键值的下投影矩阵,形状为 R d c × d \mathbb{R}^{d_c \times d} Rdc×d
根据公式(9)(10),键的生成过程为:
k t C = W U K c t K V = W U K ( W D K V h t ) = ( W U K W D K V ) h t k_t^C = W^{UK} c_t^{KV} = W^{UK} (W^{DKV} h_t) = (W^{UK} W^{DKV}) h_t ktC=WUKctKV=WUK(WDKVht)=(WUKWDKV)ht
这里, W U K W^{UK} WUK 和 W D K V W^{DKV} WDKV 可合并为一个新的矩阵 W ′ Q = W U K W D K V W'^Q = W^{UK} W^{DKV} W′Q=WUKWDKV,使得:
k t C = W ′ Q h t k_t^C = W'^Q h_t ktC=W′Qht
此时,生成键的过程被转化为一次矩阵乘法,等价于将 W U K W^{UK} WUK 的操作“吸收”到 W Q W^Q WQ 中(实际是与 W Q W^Q WQ 合并)。同理,值的生成矩阵 W U V W^{UV} WUV 可与输出投影矩阵 W O W^O WO 合并,避免显式计算 v t C v_t^C vtC。 -
举例说明(简化维度)
假设:- d = 512 d = 512 d=512(输入维度), d c = 128 d_c = 128 dc=128(KV压缩维度), d h n h = 1024 d_h n_h = 1024 dhnh=1024(单头维度×头数)
- W D K V W^{DKV} WDKV 是 128 × 512 128×512 128×512 的下投影矩阵, W U K W^{UK} WUK 是 1024 × 128 1024×128 1024×128 的键上投影矩阵
标准MHA流程(需显式计算键):
- c t K V = W D K V h t c_t^{KV} = W^{DKV} h_t ctKV=WDKVht(128维向量)
- k t C = W U K c t K V k_t^C = W^{UK} c_t^{KV} ktC=WUKctKV(1024维键,需存储)
MLA优化后(吸收矩阵,跳过键计算):
- 合并矩阵: W ′ Q = W U K W D K V W'^Q = W^{UK} W^{DKV} W′Q=WUKWDKV(形状为 1024 × 512 1024×512 1024×512)
- 直接计算: k t C = W ′ Q h t k_t^C = W'^Q h_t ktC=W′Qht(无需单独存储 W U K W^{UK} WUK 和 c t K V c_t^{KV} ctKV,推理时仅需缓存 c t K V c_t^{KV} ctKV)
数学推导与示例
1. 键(Key)的融合
• 原始计算:
k t C = W U K ⋅ c t K V = W U K ⋅ ( W D K V ⋅ h t ) k_t^C = W^{UK} \cdot c_t^{KV} = W^{UK} \cdot (W^{DKV} \cdot h_t) ktC=WUK⋅ctKV=WUK⋅(WDKV⋅ht)
• 合并权重:
将 W U K ⋅ W D K V W^{UK} \cdot W^{DKV} WUK⋅WDKV合并为新的查询权重矩阵 W Q ′ W^{Q'} WQ′:
W Q ′ = W Q ⋅ ( W U K ⋅ W D K V ) W^{Q'} = W^Q \cdot (W^{UK} \cdot W^{DKV}) WQ′=WQ⋅(WUK⋅WDKV)
此时,查询计算简化为:
q t ′ = W Q ′ ⋅ h t q_t' = W^{Q'} \cdot h_t qt′=WQ′⋅ht
实际计算注意力时,直接使用 q t ′ q_t' qt′,无需单独存储 k t C k_t^C ktC。
2. 值(Value)的融合
• 原始计算:
v t C = W U V ⋅ c t K V = W U V ⋅ ( W D K V ⋅ h t ) v_t^C = W^{UV} \cdot c_t^{KV} = W^{UV} \cdot (W^{DKV} \cdot h_t) vtC=WUV⋅ctKV=WUV⋅(WDKV⋅ht)
• 合并到输出矩阵:
将 W U V ⋅ W D K V W^{UV} \cdot W^{DKV} WUV⋅WDKV合并到输出矩阵 W O W^O WO中:
W O ′ = W O ⋅ ( W U V ⋅ W D K V ) W^{O'} = W^O \cdot (W^{UV} \cdot W^{DKV}) WO′=WO⋅(WUV⋅WDKV)
最终输出计算为:
u t = W O ′ ⋅ Attention ( q t ′ , k t ′ , v t ′ ) u_t = W^{O'} \cdot \text{Attention}(q_t', k_t', v_t') ut=WO′⋅Attention(qt′,kt′,vt′)
实例说明
假设模型参数为:
• 输入维度 d = 512 d=512 d=512,压缩维度 d c = 128 d_c=128 dc=128,头数 n h = 8 n_h=8 nh=8,每头维度 d h = 64 d_h=64 dh=64。
• W D K V ∈ R 128 × 512 W^{DKV} \in \mathbb{R}^{128 \times 512} WDKV∈R128×512, W U K ∈ R 512 × 128 W^{UK} \in \mathbb{R}^{512 \times 128} WUK∈R512×128, W Q ∈ R 512 × 512 W^Q \in \mathbb{R}^{512 \times 512} WQ∈R512×512。
推理优化步骤:
-
合并键的投影:
W Q ′ = W Q ⋅ ( W U K ⋅ W D K V ) ∈ R 512 × 512 W^{Q'} = W^Q \cdot (W^{UK} \cdot W^{DKV}) \in \mathbb{R}^{512 \times 512} WQ′=WQ⋅(WUK⋅WDKV)∈R512×512
实际计算查询时:
q t ′ = W Q ′ ⋅ h t q_t' = W^{Q'} \cdot h_t qt′=WQ′⋅ht
原始需要存储 k t C ∈ R 512 k_t^C \in \mathbb{R}^{512} ktC∈R512,优化后直接通过 q t ′ q_t' qt′隐式包含键信息。 -
合并值的投影:
W O ′ = W O ⋅ ( W U V ⋅ W D K V ) ∈ R 512 × 512 W^{O'} = W^O \cdot (W^{UV} \cdot W^{DKV}) \in \mathbb{R}^{512 \times 512} WO′=WO⋅(WUV⋅WDKV)∈R512×512
输出计算直接使用合并后的 W O ′ W^{O'} WO′,无需单独计算值向量 v t C v_t^C vtC。
2.5.2. 解耦旋转位置嵌入(Dcoupled RoPE )
一、核心问题:传统RoPE与低秩KV压缩的冲突
DeepSeek-V2在设计MLA时遇到一个关键矛盾:
- RoPE的位置敏感性:RoPE通过旋转矩阵对键(K)和查询(Q)添加位置信息,要求键和查询在计算时携带与位置相关的参数(如不同位置的旋转矩阵 R t \mathbf{R}_t Rt)。
- 矩阵吸收失效:在MLA的低秩压缩中,键的生成需要将上投影矩阵 W U K W^{UK} WUK 融入查询投影矩阵 W Q W^Q WQ(见2.1.2节),以跳过显式计算键值对。但RoPE的旋转矩阵会插入在 W Q W^Q WQ 和 W U K W^{UK} WUK 之间,导致:
传统流程: k t C = W U K ⋅ R t ⋅ W D K V h t \text{传统流程:} \quad k_t^C = W^{UK} \cdot \mathbf{R}_t \cdot W^{DKV} h_t 传统流程:ktC=WUK⋅Rt⋅WDKVht
由于矩阵乘法不满足交换律, W U K W^{UK} WUK 无法与 W Q W^Q WQ 合并,必须为每个位置 t t t 单独计算 k t C k_t^C ktC,导致推理时需重新计算所有前缀token的键,计算量随序列长度呈平方级增长(例如128K序列时,每次生成新token需计算128K次键,效率极低)。
在DeepSeek-V2模型中,将旋转位置编码(RoPE)与低秩KV压缩技术结合时,由于矩阵乘法不满足交换律,导致推理过程中必须重新计算所有前缀token的键(Key),从而显著降低效率。以下是该问题的技术细节及实例分析:
核心矛盾:RoPE与低秩KV压缩的互斥性
-
低秩KV压缩的原理
• 压缩过程:输入向量 h t h_t ht通过低秩矩阵 W D K V ∈ R d c × d W^{DKV} \in \mathbb{R}^{d_c \times d} WDKV∈Rdc×d( d c d_c dc为压缩维度, d d d为原始维度)压缩为潜在向量 c t K V c_t^{KV} ctKV:
c t K V = W D K V ⋅ h t c_t^{KV} = W^{DKV} \cdot h_t ctKV=WDKV⋅ht
• 还原键值:通过上投影矩阵 W U K ∈ R d × d c W^{UK} \in \mathbb{R}^{d \times d_c} WUK∈Rd×dc和 W U V W^{UV} WUV还原完整键值:
k t C = W U K ⋅ c t K V , v t C = W U V ⋅ c t K V k_t^C = W^{UK} \cdot c_t^{KV}, \quad v_t^C = W^{UV} \cdot c_t^{KV} ktC=WUK⋅ctKV,vtC=WUV⋅ctKV
理想情况下,推理时可通过矩阵结合律将两步合并,例如将 W U K ⋅ W D K V W^{UK} \cdot W^{DKV} WUK⋅WDKV融入 W Q W^Q WQ,从而避免显式计算 k t C k_t^C ktC。
W Q ′ = W Q ⋅ ( W U K ⋅ W D K V ) ∈ R 512 × 512 W^{Q'} = W^Q \cdot (W^{UK} \cdot W^{DKV}) \in \mathbb{R}^{512 \times 512} WQ′=WQ⋅(WUK⋅WDKV)∈R512×512 -
RoPE的位置敏感性
• RoPE的作用:RoPE通过旋转矩阵 R t R_t Rt对查询(Query)和键(Key)引入位置相关的相位偏移:
q t = R t ⋅ ( W Q ⋅ h t ) , k t = R t ⋅ ( W U K ⋅ c t K V ) q_t = R_t \cdot (W^Q \cdot h_t), \quad k_t = R_t \cdot (W^{UK} \cdot c_t^{KV}) qt=Rt⋅(WQ⋅ht),kt=Rt⋅(WUK⋅ctKV)
• 冲突点:RoPE矩阵 R t R_t Rt与低秩矩阵 W U K W^{UK} WUK的位置耦合,导致矩阵乘法顺序不可交换。
数学推导与冲突示例
-
原始计算流程
• 键的计算:
k t C = R t ⋅ ( W U K ⋅ c t K V ) = R t ⋅ W U K ⋅ W D K V ⋅ h t k_t^C = R_t \cdot (W^{UK} \cdot c_t^{KV}) = R_t \cdot W^{UK} \cdot W^{DKV} \cdot h_t ktC=Rt⋅(WUK⋅ctKV)=Rt⋅WUK⋅WDKV⋅ht
• 理想合并:若矩阵乘法可交换,可将 W U K ⋅ W D K V W^{UK} \cdot W^{DKV} WUK⋅WDKV提前合并到 W Q W^Q WQ中:
W Q ′ = W Q ⋅ ( W U K ⋅ W D K V ) W^{Q'} = W^Q \cdot (W^{UK} \cdot W^{DKV}) WQ′=WQ⋅(WUK⋅WDKV)
此时查询计算简化为 q t ′ = R t ⋅ W Q ′ ⋅ h t q_t' = R_t \cdot W^{Q'} \cdot h_t qt′=Rt⋅WQ′⋅ht,无需显式存储 k t C k_t^C ktC。 -
实际冲突分析
• 交换律失效:由于 R t R_t Rt与 W U K W^{UK} WUK的乘法顺序不可交换,即:
R t ⋅ W U K ≠ W U K ⋅ R t R_t \cdot W^{UK} \neq W^{UK} \cdot R_t Rt⋅WUK=WUK⋅Rt
导致无法将 W U K W^{UK} WUK吸收到 W Q W^Q WQ中。
• 示例:假设 W U K ∈ R 512 × 128 W^{UK} \in \mathbb{R}^{512 \times 128} WUK∈R512×128, R t ∈ R 512 × 512 R_t \in \mathbb{R}^{512 \times 512} Rt∈R512×512,则:
R t ⋅ W U K ∈ R 512 × 128 , W U K ⋅ R t ∈ R 128 × 512 ( 维度不匹配 ) R_t \cdot W^{UK} \in \mathbb{R}^{512 \times 128}, \quad W^{UK} \cdot R_t \in \mathbb{R}^{128 \times 512} \quad (\text{维度不匹配}) Rt⋅WUK∈R512×128,WUK⋅Rt∈R128×512(维度不匹配)
即使维度匹配(如方阵),数值结果仍不同:
若 W U K = [ 1 2 3 4 ] , R t = [ 0 1 1 0 ] , 则 R t ⋅ W U K = [ 3 4 1 2 ] ≠ W U K ⋅ R t = [ 2 1 4 3 ] \text{若} \quad W^{UK} = \begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}, R_t = \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}, \quad \text{则} \quad R_t \cdot W^{UK} = \begin{bmatrix}3 & 4 \\ 1 & 2\end{bmatrix} \neq W^{UK} \cdot R_t = \begin{bmatrix}2 & 1 \\ 4 & 3\end{bmatrix} 若WUK=[1324],Rt=[0110],则Rt⋅WUK=[3142]=WUK⋅Rt=[2413]
二、解耦RoPE策略:分离位置信息的“双重表示”
为解决上述问题,DeepSeek-V2提出解耦策略:将查询和键拆分为位置无关的压缩部分(用于高效计算)和位置相关的RoPE部分(用于捕获序列顺序),两者独立处理后拼接使用。
三、关键公式与实例解析
1. 符号定义(简化维度示例)
假设:
- 输入维度 d = 512 d = 512 d=512,压缩维度 d c = 128 d_c = 128 dc=128,查询压缩维度 d c ′ = 256 d'_c = 256 dc′=256
- 注意力头数 n h = 32 n_h = 32 nh=32,每头维度 d h = 16 d_h = 16 dh=16,解耦位置维度 d h R = 8 d_h^R = 8 dhR=8(每头位置相关子空间维度)
- c t Q c_t^Q ctQ:查询的压缩潜向量(256维,来自2.1.2节的查询压缩)
- h t h_t ht:输入隐藏层向量(512维)
2. 位置相关查询 q t R q_t^R qtR 的生成(公式14)
[ q t , 1 R ; q t , 2 R ; … ; q t , 32 R ] = q t R = RoPE ( W Q R c t Q ) [q_{t,1}^R; q_{t,2}^R; \dots; q_{t,32}^R] = q_t^R = \text{RoPE}\left( W^{QR} c_t^Q \right) [qt,1R;qt,2R;…;qt,32R]=qtR=RoPE(WQRctQ)
- W Q R W^{QR} WQR:投影矩阵(形状 32 × 8 × 256 32 \times 8 \times 256 32×8×256,将256维压缩查询投影到32头×8维的位置子空间)
- 实例:
- c t Q = [ x 1 , x 2 , . . . , x 256 ] c_t^Q = [x_1, x_2, ..., x_{256}] ctQ=[x1,x2,...,x256](压缩后的查询)
- W Q R c t Q W^{QR} c_t^Q WQRctQ 生成32个8维向量(每头一个),经RoPE添加位置信息后,得到每头的位置相关查询 q t , i R ∈ R 8 q_{t,i}^R \in \mathbb{R}^8 qt,iR∈R8。
3. 共享位置键 k t R k_t^R ktR 的生成(公式15)
k t R = RoPE ( W K R h t ) k_t^R = \text{RoPE}\left( W^{KR} h_t \right) ktR=RoPE(WKRht)
- W K R W^{KR} WKR:投影矩阵(形状 8 × 512 8 \times 512 8×512,将512维输入投影到8维位置空间)
- 实例:
- h t h_t ht 经 W K R W^{KR} WKR 投影为8维向量,再经RoPE处理,得到共享的位置键 k t R ∈ R 8 k_t^R \in \mathbb{R}^8 ktR∈R8(所有头共用,减少参数和计算量)。
4. 查询与键的拼接(公式16-17)
q t , i = [ q t , i C ; q t , i R ] , k t , i = [ k t , i C ; k t R ] q_{t,i} = [q_{t,i}^C; q_{t,i}^R], \quad k_{t,i} = [k_{t,i}^C; k_t^R] qt,i=[qt,iC;qt,iR],kt,i=[kt,iC;ktR]
- 实例:
- 压缩部分 q t , i C ∈ R 16 q_{t,i}^C \in \mathbb{R}^{16} qt,iC∈R16(每头原始维度),位置部分 q t , i R ∈ R 8 q_{t,i}^R \in \mathbb{R}^8 qt,iR∈R8,拼接后查询维度为 16 + 8 = 24 16+8=24 16+8=24。
- 键的压缩部分 k t , i C ∈ R 16 k_{t,i}^C \in \mathbb{R}^{16} kt,iC∈R16,位置部分 k t R ∈ R 8 k_t^R \in \mathbb{R}^8 ktR∈R8,拼接后键维度为 16 + 8 = 24 16+8=24 16+8=24。
5. 注意力计算(公式18)
o t , i = ∑ j = 1 t Softmax j ( q t , i T k j , i 24 ) v j , i C o_{t,i} = \sum_{j=1}^t \text{Softmax}_j \left( \frac{q_{t,i}^T k_{j,i}}{\sqrt{24}} \right) v_{j,i}^C ot,i=j=1∑tSoftmaxj(24qt,iTkj,i)vj,iC
- 分母 d h + d h R = 16 + 8 = 24 \sqrt{d_h + d_h^R} = \sqrt{16+8} = \sqrt{24} dh+dhR=16+8=24 是拼接后维度的归一化因子,确保注意力分数稳定。
四、核心优势:通过“分离-拼接”实现高效与位置建模的双赢
-
保留矩阵吸收(高效推理):
- 压缩部分 q t C , k t C q_t^C, k_t^C qtC,ktC 不含位置信息,其投影矩阵 W U K , W U V W^{UK}, W^{UV} WUK,WUV 仍可被吸收到 W Q , W O W^Q, W^O WQ,WO 中(如 W Q = W U Q ⋅ W D Q W^Q = W^{UQ} \cdot W^{DQ} WQ=WUQ⋅WDQ),避免重新计算前缀键。
- 实例:若序列长度为128K,传统RoPE需缓存 2 × 32 × 16 × 128 K × l 2 \times 32 \times 16 \times 128K \times l 2×32×16×128K×l 个元素,而解耦策略仅需缓存 ( 128 + 8 ) × l × 128 K (128 + 8) \times l \times 128K (128+8)×l×128K 个元素,缓存量减少93.3%(与文档表1数据一致)。
-
精准位置建模:
- 位置相关部分 q t R , k t R q_t^R, k_t^R qtR,ktR 专门处理序列顺序,通过RoPE捕获长距离依赖,例如:
- 当token位置从 t t t 到 t + 1 t+1 t+1, q t R q_t^R qtR 和 q t + 1 R q_{t+1}^R qt+1R 的旋转矩阵不同,确保模型区分前后顺序。
- 位置相关部分 q t R , k t R q_t^R, k_t^R qtR,ktR 专门处理序列顺序,通过RoPE捕获长距离依赖,例如:
-
计算量控制:
- 共享键 k t R k_t^R ktR 对所有头生效,无需为每个头单独计算位置键,计算量从 O ( n h d h l ) O(n_h d_h l) O(nhdhl) 降至 O ( ( d c + d h R ) l ) O((d_c + d_h^R) l) O((dc+dhR)l),支持128K长上下文高效处理(见文档图4,DeepSeek-V2在128K时性能稳定)。
五、与传统RoPE的对比(以1头为例)
| 步骤 | 传统RoPE(直接应用) | 解耦RoPE(MLA策略) |
|---|---|---|
| 键生成 | k t = W K h t ⋅ R t k_t = W^K h_t \cdot \mathbf{R}_t kt=WKht⋅Rt(含位置矩阵) | k t = [ k t C ; k t R ] k_t = [k_t^C; k_t^R] kt=[ktC;ktR]( k t C k_t^C ktC 无位置, k t R k_t^R ktR 含RoPE) |
| 矩阵吸收 | 不可吸收( R t \mathbf{R}_t Rt 阻断) | 可吸收( k t C k_t^C ktC 的 W U K W^{UK} WUK 融入 W Q W^Q WQ) |
| 前缀键重计算 | 每次生成新token需重算所有历史键 | 仅需计算一次共享 k t R k_t^R ktR, k t C k_t^C ktC 可快速生成 |
| KV缓存(1层) | 2 × 16 × 1 = 32 2 \times 16 \times 1 = 32 2×16×1=32 元素 | 128 ( d c ) + 8 ( d h R ) = 136 128(d_c) + 8(d_h^R) = 136 128(dc)+8(dhR)=136 元素(虽略增,但远低于MHA的 2 × 16 × 32 = 1024 2 \times 16 \times 32 = 1024 2×16×32=1024 元素) |
六、总结:解耦策略如何让MLA“两全其美”
通过将位置信息从压缩的键/查询中分离,解耦RoPE策略实现了三大突破:
- 技术兼容:在低秩KV压缩的同时,保留RoPE的位置建模能力,避免传统RoPE导致的推理瓶颈。
- 效率提升:通过矩阵吸收和共享位置键,将键值对的计算复杂度从 O ( n 2 ) O(n^2) O(n2) 降至 O ( n ) O(n) O(n),支持128K长上下文高效生成。
- 性能保障:实验表明(见文档附录D.2),解耦后的MLA在保持KV缓存大幅减少的同时,性能优于传统MHA,实现了“高效+强性能”的平衡。
这一设计是DeepSeek-V2能在长上下文场景(如128K序列)中保持高吞吐量的关键技术之一,也是其架构创新的核心亮点。
2.5.3.MLA完整计算过程
为了展示MLA的完整计算过程,我们在下面给出其完整公式:

其中,蓝色框选的向量在生成时需要缓存。在推理过程中,原始公式需要从 c t K V c_{t}^{K V} ctKV 中恢复 k t c k_{t}^{c} ktc 和 v t c v_{t}^{c} vtc 用于注意力计算。幸运的是,由于矩阵乘法的结合律,我们可以将 W U K W^{U K} WUK 合并到 W U Q W^{UQ} WUQ 中,将 W U V W^{U V} WUV 合并到 w o w^{o} wo 中。因此,我们无需为每个查询计算键值对。通过这种优化,我们避免了推理过程中重新计算 k r C k_{r}^{C} krC 和 v t C v_{t}^{C} vtC 的计算开销。
数学:矩阵分块计算,多token的矩阵分成单个token相乘
详细解释举例说明:向量与多维矩阵乘法,矩阵分块计算,多token的矩阵如何分成单个token去相乘
向量与多维矩阵乘法
定义:向量与矩阵相乘时,需满足维度匹配。若矩阵为 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n,向量为 v ∈ R n v \in \mathbb{R}^n v∈Rn,则乘积 A v Av Av 的结果为 R m \mathbb{R}^m Rm 的向量。计算方式为矩阵每行与向量的点积。
示例:
- 设矩阵 A = [ 1 2 3 4 ] A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} A=[1324],向量 v = [ 5 6 ] v = \begin{bmatrix} 5 \\ 6 \end{bmatrix} v=[56]。
- 计算 A v Av Av:
A v = [ 1 × 5 + 2 × 6 3 × 5 + 4 × 6 ] = [ 17 39 ] . Av = \begin{bmatrix} 1 \times 5 + 2 \times 6 \\ 3 \times 5 + 4 \times 6 \end{bmatrix} = \begin{bmatrix} 17 \\ 39 \end{bmatrix}. Av=[1×5+2×63×5+4×6]=[1739].
矩阵分块计算
定义:将大矩阵划分为小块(子矩阵),通过块间运算简化计算。分块需满足乘法规则:若 A A A 分块为 [ A i j ] [A_{ij}] [Aij], B B B 分块为 [ B j k ] [B_{jk}] [Bjk],则乘积 C = A B C = AB C=AB 的块 C i k = ∑ j A i j B j k C_{ik} = \sum_j A_{ij}B_{jk} Cik=∑jAijBjk。
示例:
- 矩阵 A = [ A 11 A 12 A 21 A 22 ] A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} A=[A11A21A12A22], B = [ B 11 B 12 B 21 B 22 ] B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} B=[B11B21B12B22],其中每个子块为 2 × 2 2 \times 2 2×2 矩阵。
- 计算块 C 11 C_{11} C11:
C 11 = A 11 B 11 + A 12 B 21 . C_{11} = A_{11}B_{11} + A_{12}B_{21}. C11=A11B11+A12B21. - 所有块计算完成后,合并得到 C C C。
多Token矩阵分块处理
场景:在自然语言处理中,多个token(如词向量)按行排列成矩阵 X ∈ R k × d X \in \mathbb{R}^{k \times d} X∈Rk×d,需计算 X W XW XW( W ∈ R d × h W \in \mathbb{R}^{d \times h} W∈Rd×h)。
分块策略:
-
按行分块:将 X X X 拆分为单个token的行向量。
- 例如, X = [ — x 1 — — x 2 — ⋮ — x k — ] X = \begin{bmatrix} \text{---} \ x_1 \ \text{---} \\ \text{---} \ x_2 \ \text{---} \\ \vdots \\ \text{---} \ x_k \ \text{---} \end{bmatrix} X= — x1 —— x2 —⋮— xk — ,每个 x i ∈ R 1 × d x_i \in \mathbb{R}^{1 \times d} xi∈R1×d。
- 每个token独立计算: y i = x i W y_i = x_i W yi=xiW(结果 y i ∈ R 1 × h y_i \in \mathbb{R}^{1 \times h} yi∈R1×h)。
- 合并结果: Y = [ y 1 y 2 ⋮ y k ] ∈ R k × h Y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_k \end{bmatrix} \in \mathbb{R}^{k \times h} Y= y1y2⋮yk ∈Rk×h。
-
批量分块:将 X X X 划分为多个子矩阵,每个子矩阵含多个token。
- 例如,将 X X X 分为 X 1 ∈ R k 1 × d X_1 \in \mathbb{R}^{k_1 \times d} X1∈Rk1×d 和 X 2 ∈ R k 2 × d X_2 \in \mathbb{R}^{k_2 \times d} X2∈Rk2×d,则:
Y = [ X 1 W X 2 W ] . Y = \begin{bmatrix} X_1W \\ X_2W \end{bmatrix}. Y=[X1WX2W].
示例:
- 例如,将 X X X 分为 X 1 ∈ R k 1 × d X_1 \in \mathbb{R}^{k_1 \times d} X1∈Rk1×d 和 X 2 ∈ R k 2 × d X_2 \in \mathbb{R}^{k_2 \times d} X2∈Rk2×d,则:
- 设 X = [ 1 2 3 4 5 6 ] X = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} X= 135246 , W = [ 0.5 1 1.5 2 ] W = \begin{bmatrix} 0.5 & 1 \\ 1.5 & 2 \end{bmatrix} W=[0.51.512]。
- 按行分块:
- x 1 = [ 1 2 ] → y 1 = [ 1 × 0.5 + 2 × 1.5 , 1 × 1 + 2 × 2 ] = [ 3.5 , 5 ] x_1 = [1\ 2] \rightarrow y_1 = [1 \times 0.5 + 2 \times 1.5,\ 1 \times 1 + 2 \times 2] = [3.5,\ 5] x1=[1 2]→y1=[1×0.5+2×1.5, 1×1+2×2]=[3.5, 5]。
- 同理计算 x 2 , x 3 x_2, x_3 x2,x3,合并得 Y = [ 3.5 5 8.5 11 13.5 17 ] Y = \begin{bmatrix} 3.5 & 5 \\ 8.5 & 11 \\ 13.5 & 17 \end{bmatrix} Y= 3.58.513.551117 。
分块计算的优势
- 并行计算:不同块可分配到多个处理器加速计算。
- 内存优化:处理大矩阵时,分块减少内存占用。
- 灵活性:支持动态加载数据,适合分布式系统。
总结
- 向量乘矩阵:按行或列的点积计算。
- 矩阵分块:通过子矩阵运算简化复杂计算。
- 多Token处理:按行分块后独立计算,或批量处理子矩阵,灵活平衡效率与资源。
