当前位置：首页 > ops >正文

力扣（电话号码的字母组合）

ops 2025/8/20 13:17:48

解析 LeetCode 17. 电话号码的字母组合：回溯算法的经典应用

一、题目分析

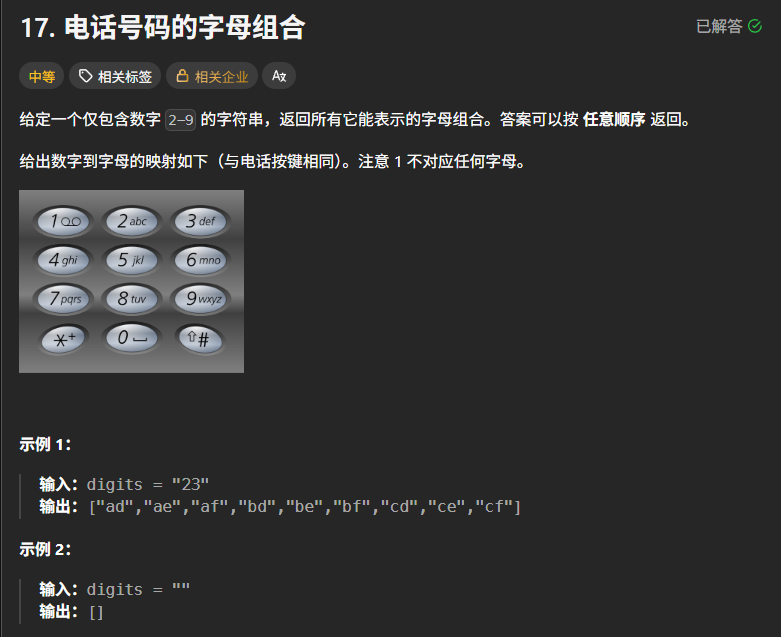
在这里插入图片描述

（一）问题定义

给定仅包含数字 2-9 的字符串 digits，返回其所有可能的字母组合（数字到字母的映射与电话按键一致）。例如，digits = "23" 时，输出 ["ad","ae","af","bd","be","bf","cd","ce","cf"] 。

（二）核心挑战

组合遍历：需枚举数字字符串中每个数字对应的所有字母的组合，保证不重复、不遗漏。
动态选择与回溯：在遍历过程中，需为每个数字选择对应的字母，递归深入后再“回溯”（撤销选择），尝试其他可能性。
边界处理：处理空输入（digits 为空时返回空列表），以及递归终止条件的判断。

二、算法思想：回溯算法的深度遍历

（一）回溯算法的核心

回溯算法是一种**深度优先搜索（DFS）**的变体，其核心思想是：

选择：在当前步骤，做出一个选择（如为当前数字选一个字母），并递归进入下一层。
回溯：递归返回后，撤销当前选择，尝试其他选择，直到遍历所有可能性。

这种“选 -> 递归 -> 撤销选”的流程，能高效枚举所有组合，尤其适用于需遍历多组可选值的组合问题。

（二）本题的回溯逻辑

数字到字母的映射：用 Map 存储数字（键）与对应字母（值）的映射，方便快速查找。
递归终止条件：当递归深度（处理到 digits 的第几个数字）等于 digits 长度时，说明已处理完所有数字，将当前组合加入结果列表。
选择与回溯：遍历当前数字对应的所有字母，依次选择字母加入临时组合，递归处理下一个数字；递归返回后，删除最后加入的字母（回溯），继续尝试其他字母。

三、代码实现与详细解析

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;class Solution {// 存储最终结果的列表List<String> result = new ArrayList<>(); // 临时存储当前组合的可变字符串（效率高于 String）StringBuffer answer = new StringBuffer(); // 数字到字母的映射表Map<String, String> map = new HashMap<>(); // 静态代码块初始化映射表（类加载时执行，仅执行一次）{map.put("2", "abc");map.put("3", "def");map.put("4", "ghi");map.put("5", "jkl");map.put("6", "mno");map.put("7", "pqrs");map.put("8", "tuv");map.put("9", "wxyz");}public List<String> letterCombinations(String digits) {// 处理空输入：直接返回空结果if (digits == null || digits.length() == 0) { return result;}// 启动回溯，从第 0 个数字开始处理backtracking(digits, 0, digits.length()); return result;}// 回溯方法：digits-数字字符串，index-当前处理的数字索引，digitLen-数字字符串长度public void backtracking(String digits, int index, int digitLen) {// 终止条件：处理完所有数字（index 等于长度）if (index == digitLen) { // 将当前组合加入结果（转换为 String）result.add(answer.toString()); return;}// 获取当前数字对应的字母字符串（如 "2" -> "abc"）String digitLetter = map.get(Character.toString(digits.charAt(index))); // 遍历当前数字的所有字母for (int i = 0; i < digitLetter.length(); i++) { // 选择：将当前字母加入临时组合answer.append(digitLetter.charAt(i)); // 递归：处理下一个数字（index + 1）backtracking(digits, index + 1, digitLen); // 回溯：撤销选择（删除最后加入的字母）answer.deleteCharAt(answer.length() - 1); }}
}

（一）代码流程拆解

初始化：
- result 存储最终所有字母组合；answer 作为可变字符串，临时存储当前组合（避免频繁创建 String 对象）；map 初始化数字到字母的映射。
空输入处理：若 digits 为空或长度为 0，直接返回空 result 。
启动回溯：调用 backtracking 方法，从第 0 个数字（index = 0 ）开始处理。
回溯逻辑：
- 终止条件：index == digitLen 时，说明已处理完所有数字，将 answer 转换为 String 加入 result 。
- 选择与递归：获取当前数字的字母字符串，遍历每个字母，加入 answer 后递归处理下一个数字（index + 1 ）。
- 回溯：递归返回后，删除 answer 最后一个字符（撤销选择），继续遍历下一个字母。
返回结果：result 存储所有组合，作为方法返回值。

（二）关键逻辑解析

映射表初始化：用静态代码块初始化 map ，保证类加载时仅执行一次，提升效率。
StringBuffer 的使用：answer 作为可变字符串，append 和 deleteCharAt 操作时间复杂度为 O(1)（针对最后一个字符），比频繁创建 String 更高效。
回溯的本质：通过“选择 -> 递归 -> 撤销选择”的流程，枚举所有可能的字母组合。例如，处理 digits = "23" 时，先选 'a' 递归处理 '3' 的字母，返回后撤销 'a' 选 'b' ，以此类推，最终生成所有组合。