动态规划算法的欢乐密码(三):简单多状态DP问题(上)



专栏:算法的魔法世界
个人主页:手握风云
目录
一、例题讲解
1.1. 按摩师
1.2. 打家劫舍 II
1.3. 删除并获得点数
1.4. 粉刷房子
一、例题讲解
1.1. 按摩师

题目要求找到一个有名的按摩师在接收源源不断的预约请求时,如何选择最优的预约集合,使得总预约时间最长。每次预约服务之间需要休息时间,因此不能接受相邻的预约。
根据题目要求,本题的状态表示为到达i位置时,按摩师的最大预约时长,我们还可以继续细分,到达i位置时,选或者不选。我们用f[i]表示nums[i]必选,此时的最大预约时长;g[i]表示nums[i]不选,此时的最大预约时长。
如下图,如果选择i位置,由于按摩师不能接受相邻的预约,所以i-1一定是不选的,[0, i-1]这段区间的最大预约时长为g[i-1],所以f[i]=g[i-1]+nums[i]。如果i位置不选,那么i-1位置就是可选可不选的,所以g[i] = max(f[i - 1], g[i - 1])。
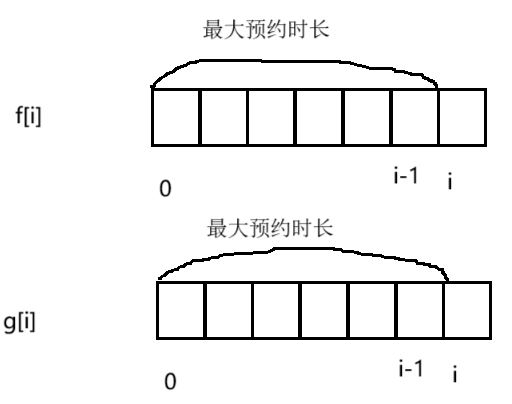
f[0]和g[0]填表的时候会发生越界,根据题目要求和状态转移方程,f[0] = nums[0],g[0] = 0。填表顺序从左往右两个表同时填写。因为最后一个位置也是可选可不选的,所以,返回值为max(f[n - 1], g[n - 1])。
完整代码实现:
class Solution {public int massage(int[] nums) {int n = nums.length;if (n == 0) {return 0;}// 定义两个数组f和g,分别存储当前状态和前一状态int[] f = new int[n];int[] g = new int[n];f[0] = nums[0];for (int i = 1; i < n; i++) {// 当前状态f[i]等于前一状态g[i-1]加上当前元素f[i] = g[i - 1] + nums[i];// 当前状态g[i]等于前一状态f[i-1]和g[i-1]中的较大值g[i] = Math.max(f[i - 1], g[i - 1]);}// 返回最后一个元素的前一状态f[n-1]和g[n-1]中的较大值return Math.max(g[n - 1], f[n - 1]);}
}1.2. 打家劫舍 II

给定一个非负整数数组(代表沿街房屋内的现金金额),房屋围成一圈(即第一个房屋与最后一个房屋相邻)。小偷需在不触发警报的前提下(相邻房屋不能同时被偷),计算当晚能偷窃到的最高金额。
看到这道题,我们先回顾下力扣第198题打家劫舍,与这一题不同的是,房屋之间不连着。每一家我们也是可以选择偷或者不偷,如果第i家选择偷,那么第i-1家就不能偷;如果第i不偷,那么i-1家可偷可不偷。
回来看这一题,当第0个位置选择偷时,那么第1个位置和第n-1个位置就不能偷,从第2个位置开始进行一次线性打家劫舍就可以;如果第0个位置选择不偷,那么只需从第1个位置到n-1个位置进行一次线性打家劫舍就可以。再从中选出两个最大值。
本题的状态表示为,当到达i位置时,偷到的最大金额。f[i]表示到达i位置时选择偷的最大金额,g[i]表示到达i位置时选择不偷的最大金额。当i位置选择偷时,由于i-1位置不能偷,所以f[i]=g[i-1]+nums[i]。当i位置选择不偷时,那么i-1可偷可不偷,g[i]=max(f[i-1], g[i-1])。f[0]=nums[0],g[0]=0。填表顺序从左向右。
完整代码实现:
class Solution {public int rob(int[] nums) {int n = nums.length;return Math.max(nums[0] + rob1(nums, 2, n - 2), rob1(nums, 1, n - 1));}private int rob1(int[] nums, int left, int right) {if (left > right) {return 0;}int n = nums.length;// 定义两个数组f和g,用于存储动态规划的结果int[] f = new int[n];int[] g = new int[n];f[left] = nums[left];for (int i = left + 1; i <= right; i++) {// f[i]表示偷到第i个房子时的最大收益,等于g[i-1]加上第i个房子的值f[i] = g[i - 1] + nums[i];g[i] = Math.max(g[i - 1], f[i - 1]);// g[i]表示偷到第i个房子时的最大收益,等于g[i-1]和f[i-1]中的较大值}return Math.max(f[right], g[right]);}
}1.3. 删除并获得点数
从一个数组中选择数字获得点数。每次选择一个数字 x,你得到 x 点,但所有 x-1 和 x+1 的数字都会被自动移除,且不获得点数。你需要找到一个策略,使得你最终获得的总点数最大。
当我们选择了某个数字x后,就必须删除与它相邻的x-1和x+1,此时我们就可以按照打家劫舍的方式来解决。但有可能给的数组里的数字不是连续的,例如[1, 2, 2, 4, 4, 5, 7, 7],就不能按照上题的思路。我们可以先用一个数组arr来预处理一下,利用数组下标来表示该下标在nums数组的总和。

那么,状态表示为,f[i]表示i位置选获得的最大点数,g[i]表示i位置不选获得的最大点数。当i位置选择时,由于i-1位置也需要同时删除,所以f[i]=g[i-1]+nums[i]。当i位置不选时,那么i-1可选可不选,g[i]=max(f[i-1], g[i-1])。f[0]=nums[0],g[0]=0。填表顺序从左向右。
完整代码实现:
class Solution {public int deleteAndEarn(int[] nums) {int n = 10_001;int[] arr = new int[n];for (int i : nums) {arr[i] += i;}// 定义两个长度为10001的数组f和g,用于存储动态规划的结果int[] f = new int[n];int[] g = new int[n];// 初始化f[0]为数组arr的第一个元素f[0] = arr[0];for (int i = 1; i < n; i++) {// f[i]表示选择当前数字i时的最大收益f[i] = g[i - 1] + arr[i];// g[i]表示不选择当前数字i时的最大收益g[i] = Math.max(f[i - 1], g[i - 1]);}// 返回f[n-1]和g[n-1]中的较大值,即为最大收益return Math.max(f[n - 1], g[n - 1]);}
}1.4. 粉刷房子

你需要从第一栋房子开始,逐个决定每栋房子的粉刷颜色,同时确保相邻房子的颜色不同,并最终使得所有房子粉刷完毕的总成本最小。注意,矩阵的行代表房间数,列0、1、2分别代表红、蓝、绿三种颜色。
每个位置都有3中颜色可以选择,那么状态表示dp[i][0]、dp[i][1]、dp[i][2],粉刷到i位置时,最后一个房子粉刷为红色、蓝色、绿色,此时的最小花费。当第i个房子粉刷为红色时,需要花费costs[i][0],那么前一个位置就需要粉刷为绿色或者蓝色,接下来的问题就变成了从0到i-1位置时粉刷成绿色或者蓝色的最小花费,所以dp[i][0]=min(dp[i-1][1], dp[i-1][2]) + costs[i][0]。同理,另外两个状态转移方程为dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i- 1][1]、dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i- 1][2]。初始化的时候,因为每一行的状态表示都依赖前一个位置,所以我们在每一行前面都加上一个虚拟节点防止越界。比如dp[0][1]需要dp[1][0]和dp[2][0]之间的最小值,所以这两个位置都初始化为0,同理dp[0][0]也初始化为0。填表顺序,从左向右一次填写3个表。最后需要返回3个dp表最后一个位置的最小值。
完整代码实现:
class Solution {public int minCost(int[][] costs) {// 获取costs数组的长度int n = costs.length;// 创建一个二维数组dp,用于存储每个位置的最小花费int[][] dp = new int[n + 1][3];// 遍历costs数组for (int i = 1; i <= n; i++) {// 计算当前位置的最小花费dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i- 1][0];dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i- 1][1];dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i- 1][2];}// 返回最后一个位置的最小花费return Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2]));}
}