后缀树:字符串处理的利器
后缀树:字符串处理的利器
今天我们来聊聊一个在字符串处理领域非常强大的数据结构——后缀树。想象一下,你有一本厚厚的字典,想要快速查找某个单词的所有出现位置,或者找出两个长文本的共同子串。这就像在一个巨大的迷宫中寻找特定的路径,而后缀树就是那个能帮你快速导航的神奇地图。
1. 什么是后缀树?
理解了后缀树的应用场景后,我们来看看它的基本概念。后缀树是一种压缩的字典树(Trie),它存储了一个字符串的所有后缀。听起来可能有点抽象,让我们用一个简单的例子来说明。
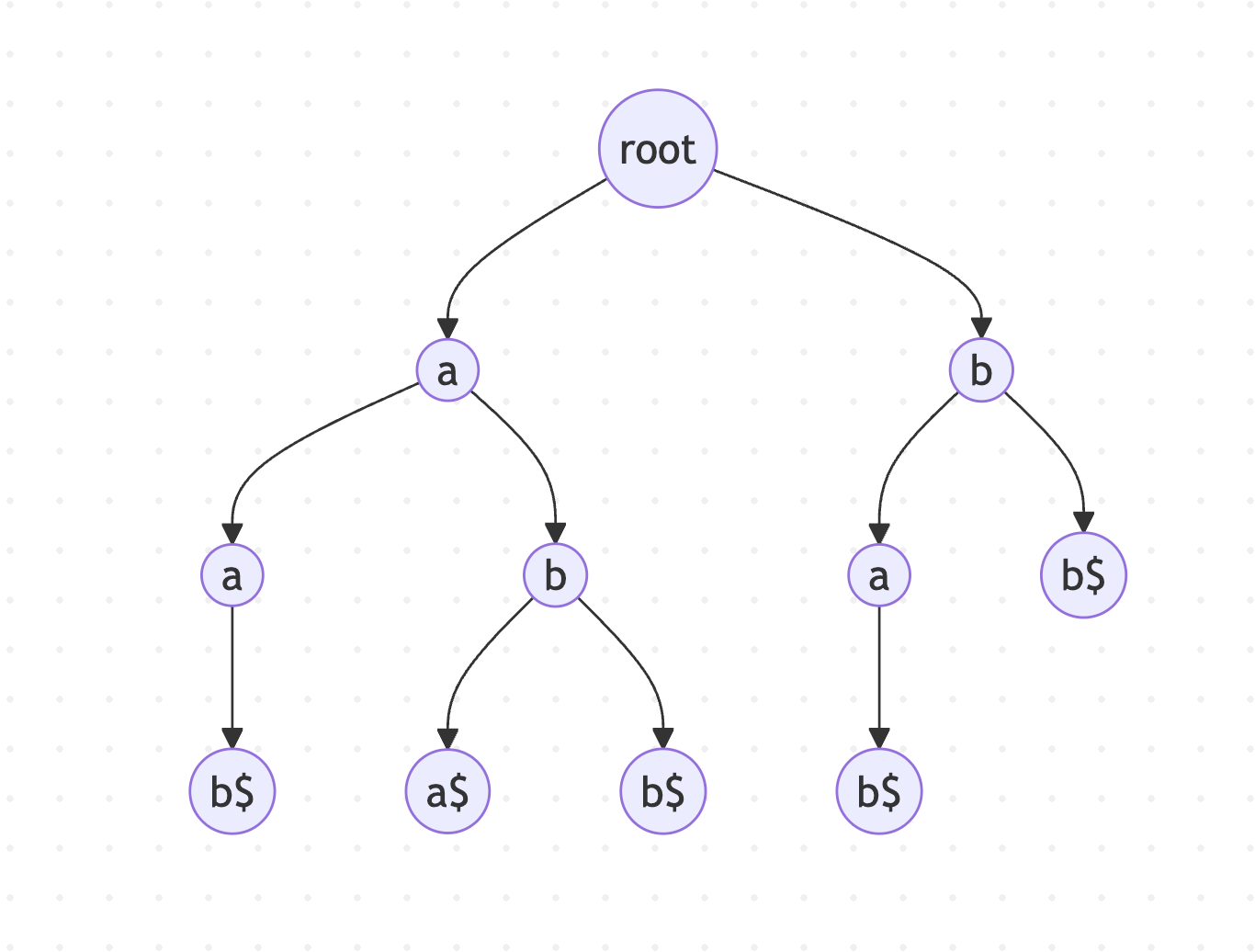
图1:字符串"aabab"的后缀树结构示意图
上面这个简单的图展示了字符串"aabab"的后缀树。每个从根节点到叶子节点的路径都代表字符串的一个后缀。后缀树的神奇之处在于,它不仅能高效存储所有后缀,还能支持各种快速的字符串查询操作。
1.1 后缀树的基本性质
后缀树有几个关键性质值得我们注意:
- 每个内部节点(非根非叶子)至少有两个子节点
- 每条边代表一个子字符串
- 所有后缀都对应从根到某个叶子节点的路径
- 构建完成后,可以在线性时间内完成各种查询
2. 后缀树的构建过程
了解了后缀树的基本概念后,我们来看看它是如何构建的。构建后缀树最著名的算法是Ukkonen算法,它能在O(n)时间内在线性构建后缀树。
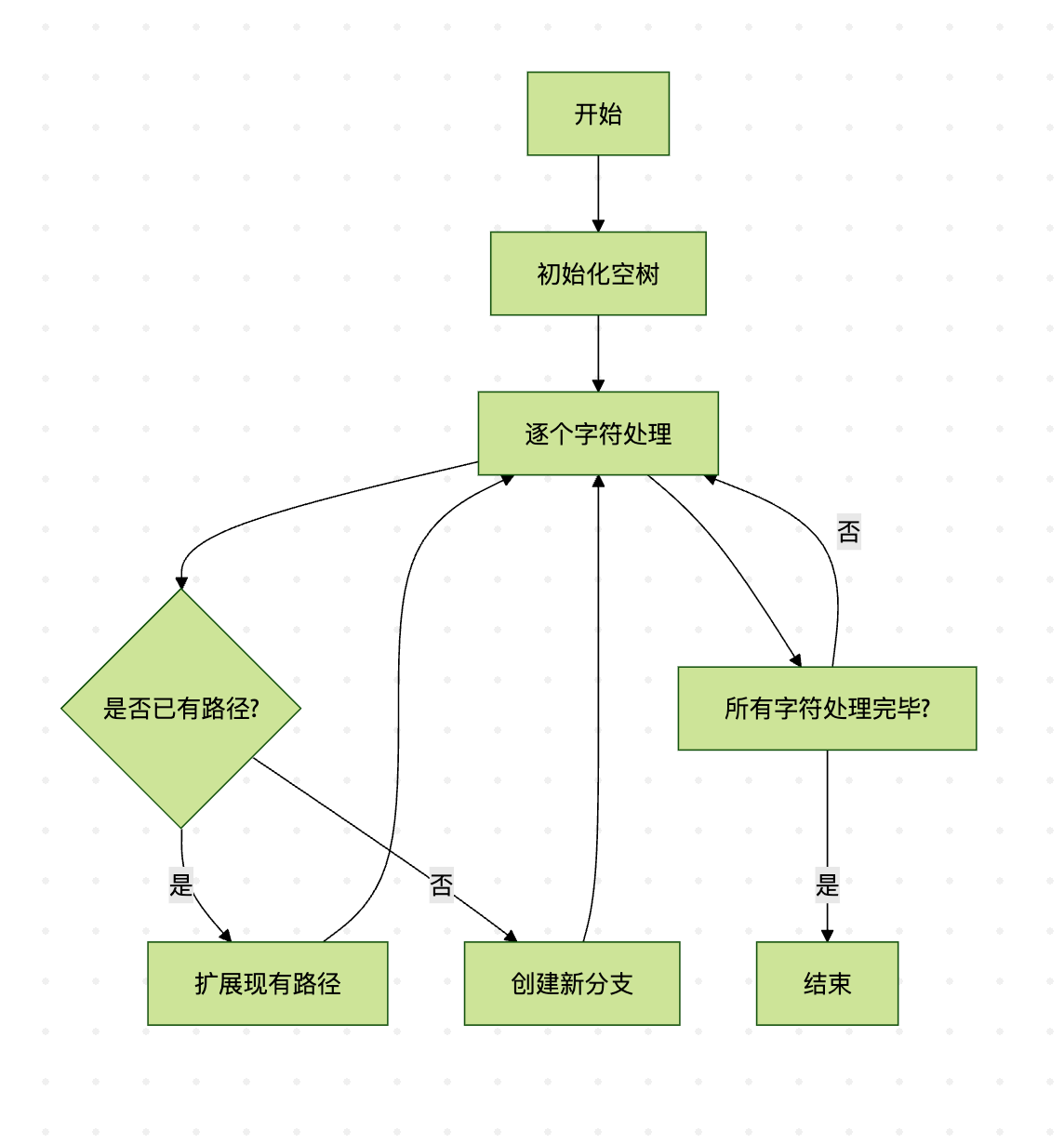
图2:后缀树构建的基本流程
Ukkonen算法的核心思想是逐步构建隐式后缀树,并在每一步中维护活动点(active point),通过三种不同的扩展规则来处理字符的添加。
2.1 Ukkonen算法实现示例
下面是一个简化的Python实现,展示了Ukkonen算法的基本思路:
class SuffixTreeNode:def __init__(self):self.children = {}self.suffix_link = Noneself.start = Noneself.end = Noneself.index = -1class SuffixTree:def __init__(self, text):self.text = textself.root = SuffixTreeNode()self.build_tree()def build_tree(self):n = len(self.text)self.root.end = 0self.active_node = self.rootself.active_edge = -1self.active_length = 0self.remaining = 0for i in range(n):self.extend_tree(i)def extend_tree(self, pos):# 算法核心实现部分pass
代码1:后缀树的基本Python类结构
考虑到实际构建过程的复杂性,上面的代码只是一个框架。完整的Ukkonen算法实现需要考虑三种扩展规则和活动点的维护,但基本原理是通过逐个字符处理来逐步构建树结构。
3. 后缀树的应用场景
理解了后缀树的构建原理后,我们来看看它在实际中有哪些强大的应用。后缀树之所以被称为字符串处理的利器,正是因为它能高效解决许多常见的字符串问题。
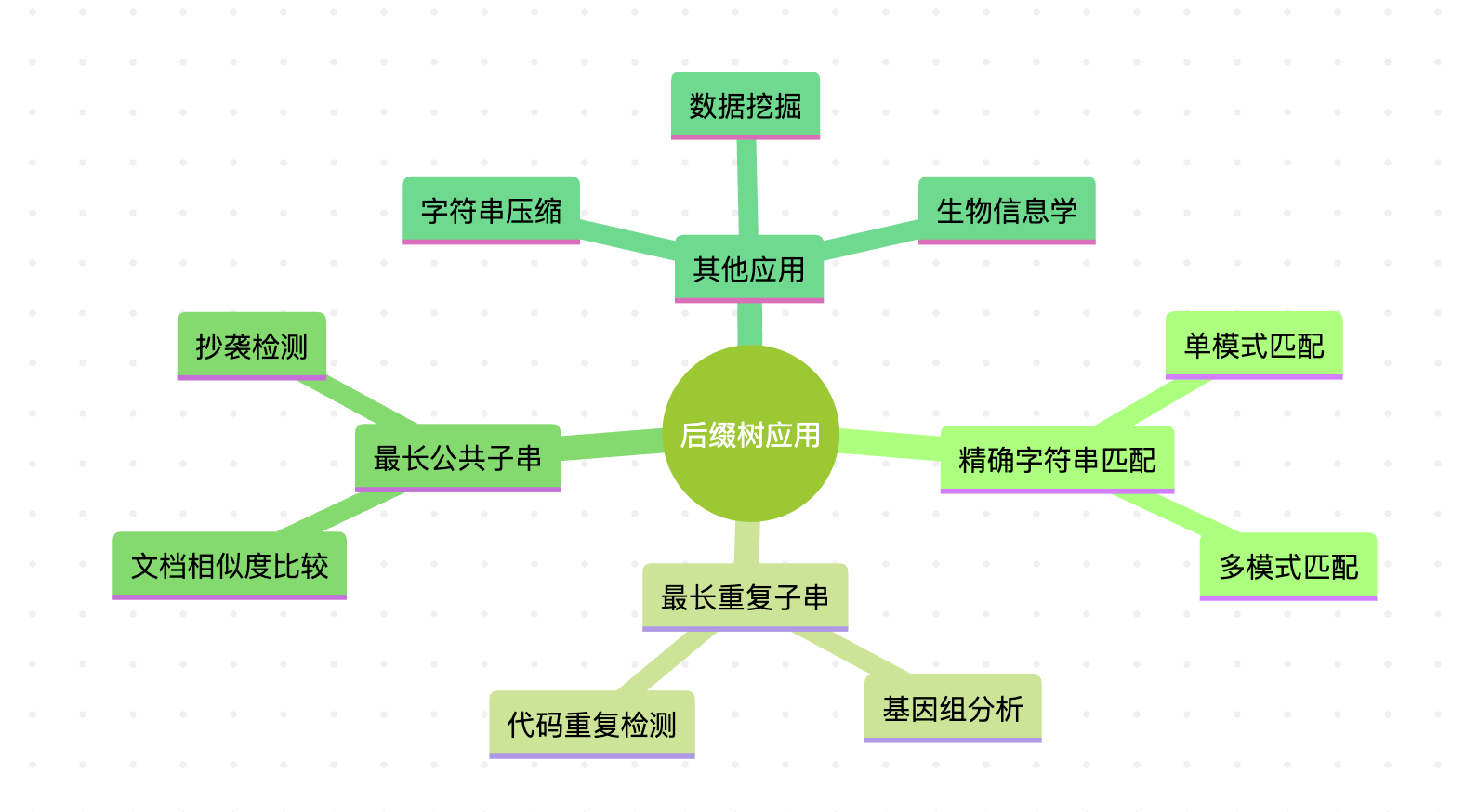
图3:后缀树的主要应用领域
3.1 最长公共子串问题
让我们看一个具体的例子:如何使用后缀树查找两个字符串的最长公共子串。传统方法需要O(n²)时间,而后缀树可以在线性时间内解决。
def find_longest_common_substring(s1, s2):# 合并字符串,用特殊字符分隔combined = s1 + '#' + s2 + '$'tree = SuffixTree(combined)# 在后缀树中查找同时包含来自两个字符串的节点的最深节点# 具体实现需要遍历树并标记节点来源# ...return longest_substring
代码2:使用后缀树查找最长公共子串的框架代码
上述代码展示了基本思路:将两个字符串合并构建后缀树,然后查找同时包含来自两个字符串的节点的最深内部节点。这个节点的路径就是从根到该节点的连接字符串,也就是最长的公共子串。
4. 后缀树与后缀数组的比较
在实际应用中,我们经常会遇到后缀树和后缀数组的选择问题。让我们来看看这两种数据结构的对比。
| 特性 | 后缀树 | 后缀数组 |
|---|---|---|
| 构建时间 | O(n) | O(n log n) |
| 空间复杂度 | 较高 | 较低 |
| 查询效率 | 极高 | 高 |
| 实现难度 | 较难 | 中等 |
从比较中可以看出,后缀树在理论性能上更优,但实现复杂且空间消耗较大;而后缀数组在实际应用中往往更受欢迎,因为它在空间效率和实现难度上更有优势,同时配合LCP数组也能达到接近后缀树的查询性能。
5. 实际应用中的优化技巧
了解了基本原理后,我们来看看在实际工程应用中如何优化后缀树的实现。我通常是这样做的,大家可以参考一下。
5.1 空间优化技巧
后缀树的一个主要问题是空间消耗大。我们可以采用以下优化方法:
class CompactSuffixTreeNode:def __init__(self):self.children = {} # 使用字典而非数组self.suffix_link = Noneself.start = None # 使用指针而非存储完整字符串self.end = None # 使用指针而非存储完整字符串# 其他优化:按需分配、压缩路径等
代码3:空间优化的后缀树节点实现
考虑到实际内存限制和性能需求,我们使用了指针而非存储完整字符串,并采用字典而非数组来存储子节点。这种优化可以显著减少内存使用,特别是对于大型文本。
5.2 并行构建策略
对于非常大的字符串,我们可以考虑并行构建后缀树:
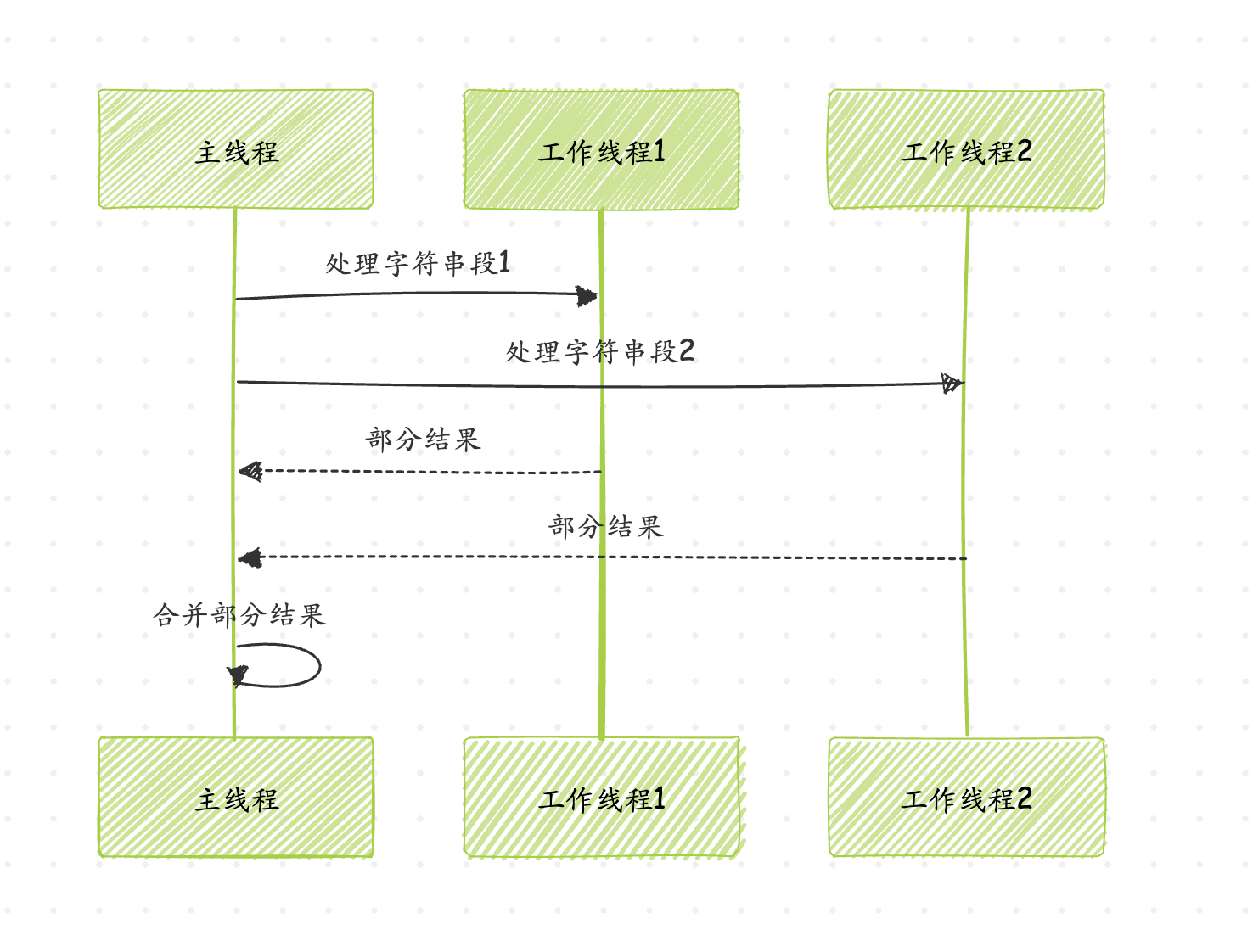
图4:并行构建后缀树的序列图
通过将字符串分段处理,然后合并部分结果,我们可以利用多核处理器加速后缀树的构建过程。这种方法特别适合处理基因组数据等超长字符串。
6. 总结
通过今天的讨论,相信大家对后缀树有了更深入的理解。让我们总结一下本文的主要内容:
- 基本概念:后缀树是一种存储字符串所有后缀的压缩字典树
- 构建算法:Ukkonen算法可以在线性时间内构建后缀树
- 应用场景:包括字符串匹配、最长公共子串、重复子串发现等
- 比较分析:与后缀数组相比各有优劣,根据场景选择
- 优化技巧:空间优化和并行构建等工程实践
后缀树是字符串处理领域的强大工具,虽然实现复杂,但掌握它能让你在处理字符串问题时如虎添翼。我建议大家可以尝试实现一个简化版本的后缀树,这将大大加深你对它的理解。
希望这篇文章能帮助大家在后缀树的学习和应用中少走弯路。如果你有任何问题或想法,欢迎随时交流讨论。让我们共同进步,探索更多高效的数据结构和算法!
