持续同调文章阅读(四)
持续同调文章阅读(四)
原文:Afra Zomorodian and Gunnar Carlsson. Computing Persistent Homology. Discrete Comput Geom 33:249–274 (2005). DOI: 10.1007/s00454-004-1146-y.
这篇2004年的文章是划时代的,Zomorodian和Carlsson研究了过滤的单纯复形的同调,并给出了在主理想整环下计算持续同调的算法,广泛应用至今。本文就这篇文章提到的在域上计算的算法做一个简单分析(对应到原文的第四章“Algorithm for Fields”),记号比较多,这里符号都沿用文章中的,含义不再赘述,具体非常建议阅读原文。我这篇阅读笔记主要是对算法的具体过程有个更详细的阐述。
构造算法是基于下面两个引理。
Lemma4.1(阶梯型): 列阶梯型的主元和标准型对角元相同。此外,两形式中主行基元的次数相同。
证明: 根据我们的排序,行基元 e^i\hat{e}_ie^i 的次数按行从上至下依次递减。在每个固定列,eje_jej 的次数是常数 ccc。从而 degMk(i,j)=c−dege^ideg M_k(i,j) = c-deg \hat{e}_idegMk(i,j)=c−dege^i,因此每一列元素的度按行递增。我们可以用行变换在不改变主元次数(也即行基元的次数)下消去主元下方的非零元素,然后通过各行列位置的交换变成对角型。
(我的注记:eje_jej 的次数是常数,因为是在同一个时刻出生。)
Corollary4.1: 令 Mk~\tilde{M_k}Mk~ 是 ∂k\partial_k∂k 的列阶梯型,对应到 CkC_kCk 的基 {ej}\{e_j \}{ej} 和 Zk−1Z_{k-1}Zk−1 的基 {e^j}\{\hat{e}_j\}{e^j}。 如果第 iii 行有主元 Mk~(i,j)=tn\tilde{M_k}(i, j) = t^nMk~(i,j)=tn,则它贡献了 Hk−1H_{k-1}Hk−1 中的 ∑degei^F[t]/tn\sum^{deg \hat{e_i}} F[t]/t^n∑degei^F[t]/tn。否则,它贡献了 ∑degei^F[t]\sum^{deg \hat{e_i}} F[t]∑degei^F[t]。等价地,我们分别得到 PPP-intervals (deg ei^,deg ei^+n)(deg\ \hat{e_i} , deg\ \hat{e_i}+n)(deg ei^,deg ei^+n) 和 (deg ei^,∞)(deg\ \hat{e_i} , \infty)(deg ei^,∞)。
这就是说,如果我们只关注基元的次数,我们可以直接从列阶梯型读出(而不必化成对角型)。
Lemma4.2(基变换): 为表示 ∂k+1\partial_{k+1}∂k+1 相对于 Ck+1C_{k+1}Ck+1 的标准基和 ZkZ_kZk 的基,只需简单删掉 Mk+1M_{k+1}Mk+1 中对应到 Mk~\tilde{M_k}Mk~ 主列的那些行。
证明: 假设我们为了消除主行 jjj 的一个元素而给第 jjj 列乘以 qqq 倍加到第 iii 列,如 fig7。这操作相当于在 MkM_kMk 中把列基元 eie_iei 替换成 ei+qeje_i+q e_jei+qej。为了在 ∂k+1\partial_{k+1}∂k+1 的行基做相同的替换,我们需要给第 iii 行乘以 −q-q−q 倍加到第 jjj 行。然而,第 jjj 行最终都会是零元素,所以这样的操作永远不会改变第 iii 行。
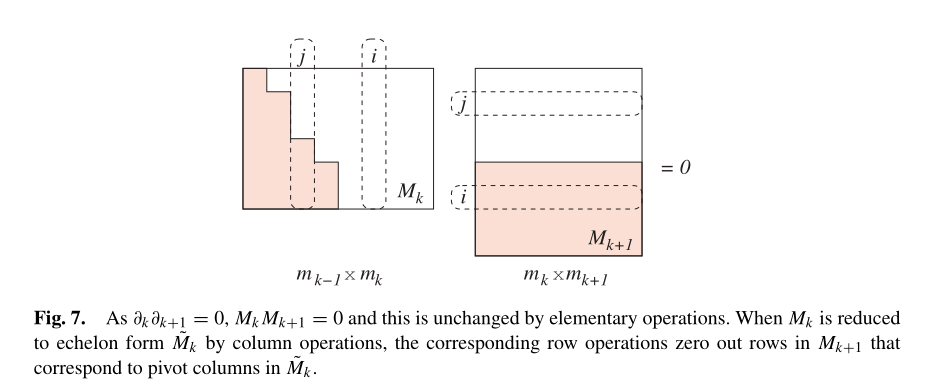
这个引理的好处在于我们不再需要做行变换。我们只需删除低一维空间中主列对应的行,就能得到 ∂k+1\partial_{k+1}∂k+1 关于 ZkZ_kZk 基的表示。
现在我们考察作者给的具体算法。我们的单纯复形列如下:
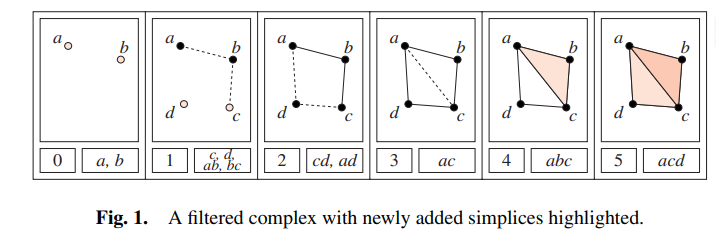
我们构造的数组结构如下:
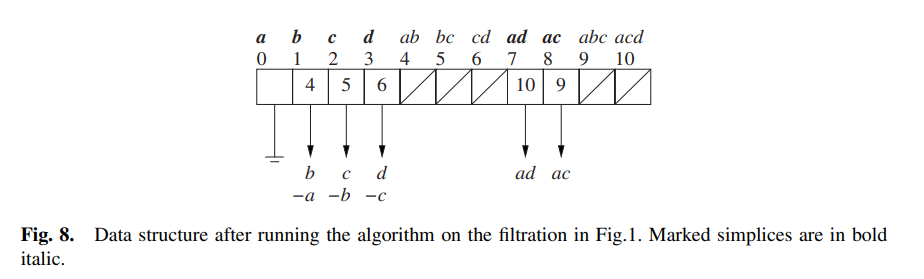
计算持续区间的整体算法如下:

上图 fig 9 疑有作者笔误,P−P-P−interval 中的 LkL_kLk 应当是 Lk−1L_{k-1}Lk−1。另外 REMOVEPIVOTROWS 操作的步骤是:

接下来我们详细地解释每一步(即 “ for j=0j=0j=0 to m−1m-1m−1” )是怎么循环的,这里作者写的比较简略。
第一步: 点 aaa 进入,由于求边缘链后自然是0, 所以标记点 aaa(也就是图8中将 aaa 标粗显示);点 b,c,db,c,db,c,d 同理;
第二步: 边 ababab 进入(j=4j=4j=4),k=1k=1k=1,求边缘链后 d=b−ad=b-ad=b−a,没有未标记项。现在 i=1i=1i=1 且 T[i]T[i]T[i] 为空,break,再次进入主循环;i=1,k=1i=1, k=1i=1,k=1,在 T[1]T[1]T[1] 记下 j=4j=4j=4 和 d=b−ad=b-ad=b−a,而 degσi=0,degσj=1deg\sigma^i=0, deg\sigma^j=1degσi=0,degσj=1(从fig1计算得到),从而更新 L0={(0,1)}L_0=\{(0,1)\}L0={(0,1)}。边 bc,cdbc, cdbc,cd 进入同理。
第三步: 边 adadad 进入(j=7j=7j=7),k=1k=1k=1,求边缘链后 d=d−ad=d-ad=d−a(记号稍显混乱),没有未标记项。i=3i=3i=3,但 T[3]T[3]T[3] 不为空,且 T[3]T[3]T[3] 中 σ3\sigma^3σ3(也就是 ddd)的系数是1,在 Z2\mathbb{Z}_2Z2 上的逆元仍是1(Z2\mathbb{Z}_2Z2是作者本章中限定的域,可以推广到一般的域),所以更新 d=d−a−(d−c)=c−ad=d-a-(d-c)=c-ad=d−a−(d−c)=c−a,此时 ddd 仍不为空,while 循环还在继续,最终能将 ddd 消成空集,这就意味着再回到主循环时,就会标记 adadad。后面就是同理的,最终得到 fig8 以及最后的持续区间(作者写这篇文章的时候还叫 P−P-P−interval)L0={(0,∞),(0,1),(1,1),(1,2)}L_0 = \{(0,\infty),(0, 1),(1, 1),(1, 2)\}L0={(0,∞),(0,1),(1,1),(1,2)} 和 L1={(2,4),(3,5)}L_1 = \{(2, 4),(3, 5)\}L1={(2,4),(3,5)}。 □\square□
注记:算法中计算 P−P-P−interval 得到 Lk−1L_{k-1}Lk−1,用到的正是 Corollary4.1;而 REMOVEPIVOTROWS 操作中,就是先根据 Lemma4.2 消元,消去未标记的复形后得到 Zk−1Z_{k-1}Zk−1 的基,然后在 while 循环中,有最大指标 i=max di = max \ di=max d 的项可能是一个潜在的主元。但 T[i]T[i]T[i] 非空的话,那一行已经有主元,所以我们将这一行从我们的链中消去。否则我们就找到了一个主元,且现在对应的链就是主列。
