二进制专项

1. 按位与（AND，运算符：&）

• 运算规则：对应位都为 1 时结果为 1，否则为 0。
• 示例：

  int a = 5;    // 二进制: 0101
  int b = 3;    // 二进制: 0011
  int result = a & b;  // 结果: 0001 (十进制1)
  

• 性质：
  • 清零特定位：n & 0 结果为 0。
  • 保留特定位：n & 1 可提取最低位（判断奇偶）。
  • 幂等性：n & n = n。

2. 按位或（OR，运算符：|）

• 运算规则：对应位中只要有一个为 1，结果为 1。
• 示例：

  int a = 5;    // 二进制: 0101
  int b = 3;    // 二进制: 0011
  int result = a | b;  // 结果: 0111 (十进制7)
  

• 性质：
  • 设置特定位：n | 1 可将最低位设为 1。
  • 包含性：结果包含两个操作数的所有 1 位。
  • 幂等性：n | n = n。

3. 按位异或（XOR，运算符：^）

• 运算规则：对应位不同时结果为 1，相同为 0。
• 示例：

  int a = 5;    // 二进制: 0101
  int b = 3;    // 二进制: 0011
  int result = a ^ b;  // 结果: 0110 (十进制6)
  

• 性质：
  • 交换律：a ^ b = b ^ a。
  • 结合律：(a ^ b) ^ c = a ^ (b ^ c)。
  • 自反性：a ^ a = 0，a ^ 0 = a。
  • 翻转特定位：n ^ 1 可翻转最低位。

4. 按位取反（NOT，运算符：~）

• 运算规则：将每一位取反（0 变 1，1 变 0）。
• 示例：

  int a = 5;    // 二进制: 0101 (假设为4位)
  int result = ~a;  // 结果: 1010 (补码表示，十进制-6)
  

• 性质：
  • 补码关系：~n = -(n+1)（对有符号数）。
  • 反转所有位：可用于构造掩码（如 ~0 生成全 1 掩码）。

5. 左移（Left Shift，运算符：<<）

• 运算规则：将所有位向左移动指定位数，右侧补 0。
• 示例：

  int a = 5;    // 二进制: 0101
  int result = a << 2;  // 结果: 010100 (十进制20)
  

• 性质：
  • 相当于乘法：n << k 等价于 n * 2^k。
  • 高位溢出丢弃：若移出位数超过类型范围，高位丢失。

6. 右移（Right Shift，运算符：>>）

• 运算规则：将所有位向右移动指定位数，左侧补位方式取决于符号：
  • 无符号数：左侧补 0（逻辑右移）。
  • 有符号数：左侧补符号位（算术右移，如负数补 1）。
• 示例：

  unsigned int a = 20;  // 二进制: 00010100
  unsigned int b = a >> 2;  // 结果: 00000101 (十进制5)int c = -8;  // 二进制补码: 11111000
  int d = c >> 2;  // 结果: 11111110 (十进制-2，算术右移)
  

• 性质：
  • 相当于除法：n >> k 等价于 n / 2^k（向下取整）。
  • 低位丢弃：右移会丢弃右侧的位数。

7. 常用技巧与应用

a. 掩码操作

• 构造掩码：生成特定位置为 1 的数，如 mask = 1 << k（第 k 位为 1）。
• 提取特定位：n & mask 可提取 n 的第 k 位。
• 设置特定位：n | mask 将 n 的第 k 位设为 1。
• 清除特定位：n & (~mask) 将 n 的第 k 位设为 0。

b. 奇偶判断

bool isOdd(int n) {return (n & 1) == 1;  // 最低位为1则为奇数
}

c. 交换两数（不使用临时变量）

a = a ^ b;
b = a ^ b;  // 此时b = a
a = a ^ b;  // 此时a = b

d. 计算 2 的幂

int powerOfTwo(int k) {return 1 << k;  // 2^k
}

e. 统计二进制中 1 的个数

int countBits(int n) {int count = 0;while (n) {count += n & 1;  // 累加最低位n >>= 1;         // 右移一位}return count;
}// 更高效的方法（Brian Kernighan算法）
int countBitsFaster(int n) {int count = 0;while (n) {n &= (n - 1);  // 清除最低位的1count++;}return count;
}

8. 优先级注意事项

位运算符的优先级低于算术运算符（如 +, -），但高于逻辑运算符（如 &&, ||）。使用时需注意括号，例如：

int result = a & b + c;  // 先计算 b + c，再与 a 按位与
int result = (a & b) + c;  // 先按位与，再加 c

9. 常见错误

1. 混淆按位与（&）和逻辑与（&&）：
   • & 是二进制位运算，&& 是逻辑条件判断。
2. 右移负数的符号扩展：
   • 有符号数右移可能导致符号扩展（补 1），需注意。
3. 移位溢出：
   • 移位位数超过类型位数（如 int 移 32 位）会导致未定义行为。

10.扩展函数

计算无符号整数中 1 的个数。

__builtin_popcount 函数

原型

int __builtin_popcount(unsigned int x);

示例

#include <iostream>
using namespace std;int main() {unsigned int x = 15;  // 二进制: 1111cout << "__builtin_popcount(15) = " << __builtin_popcount(x) << endl;  // 输出: 4return 0;
}

注意事项

• 参数类型：参数必须是无符号整数（unsigned int）。若传入有符号数或其他类型，可能导致意外结果。
• 位数限制：该函数仅计算 32 位整数中的 1 的个数。若需处理 64 位整数，使用 __builtin_popcountll。

处理 64 位整数

int __builtin_popcountll(unsigned long long x);  // 计算64位整数的1的个数

 查找第一个 1 的位置

int __builtin_ctz(unsigned int x);   // 计算末尾连续0的个数（Trailing Zero Count）
int __builtin_clz(unsigned int x);   // 计算前导连续0的个数（Leading Zero Count）
int __builtin_ffs(unsigned int x);   // 查找第一个1的位置（从1开始计数，相当于 __builtin_ctz(x) + 1）

处理 64 位版本

int __builtin_ctzll(unsigned long long x);  // 64位版本的 __builtin_ctz
int __builtin_clzll(unsigned long long x);  // 64位版本的 __builtin_clz

检查溢出

bool __builtin_add_overflow(a, b, &result);  // 检查加法是否溢出
bool __builtin_mul_overflow(a, b, &result);  // 检查乘法是否溢出
// 类似的还有减法、左移等

测试特定位

bool __builtin_parity(unsigned int x);    // 判断1的个数的奇偶性（奇数返回1，偶数返回0）
bool __builtin_parityll(unsigned long long x);  // 64位版本

位反转

unsigned int __builtin_bswap32(unsigned int x);  // 32位整数按字节反转（大端<->小端）
unsigned long long __builtin_bswap64(unsigned long long x);  // 64位版本

unsigned int x = 0x12345678;
unsigned int reversed = __builtin_bswap32(x);  // 结果: 0x78563412

预测分支方向

__builtin_expect(long exp, long c);  // 告诉编译器exp==c的概率，帮助优化分支预测

if (__builtin_expect(x == 0, 0)) {  // 告诉编译器x==0的概率很低// 执行罕见情况的代码
}

高效内存设置

void* __builtin_memset(void* s, int c, size_t n);  // 比标准库的memset更高效

内存复制

void* __builtin_memcpy(void* dest, const void* src, size_t n);  // 比标准库的memcpy更高效

浮点快速平方根

float __builtin_sqrtf(float x);     // 单精度浮点数平方根
double __builtin_sqrt(double x);    // 双精度浮点数平方根

浮点取整

double __builtin_floor(double x);   // 向下取整
double __builtin_ceil(double x);    // 向上取整

例题 

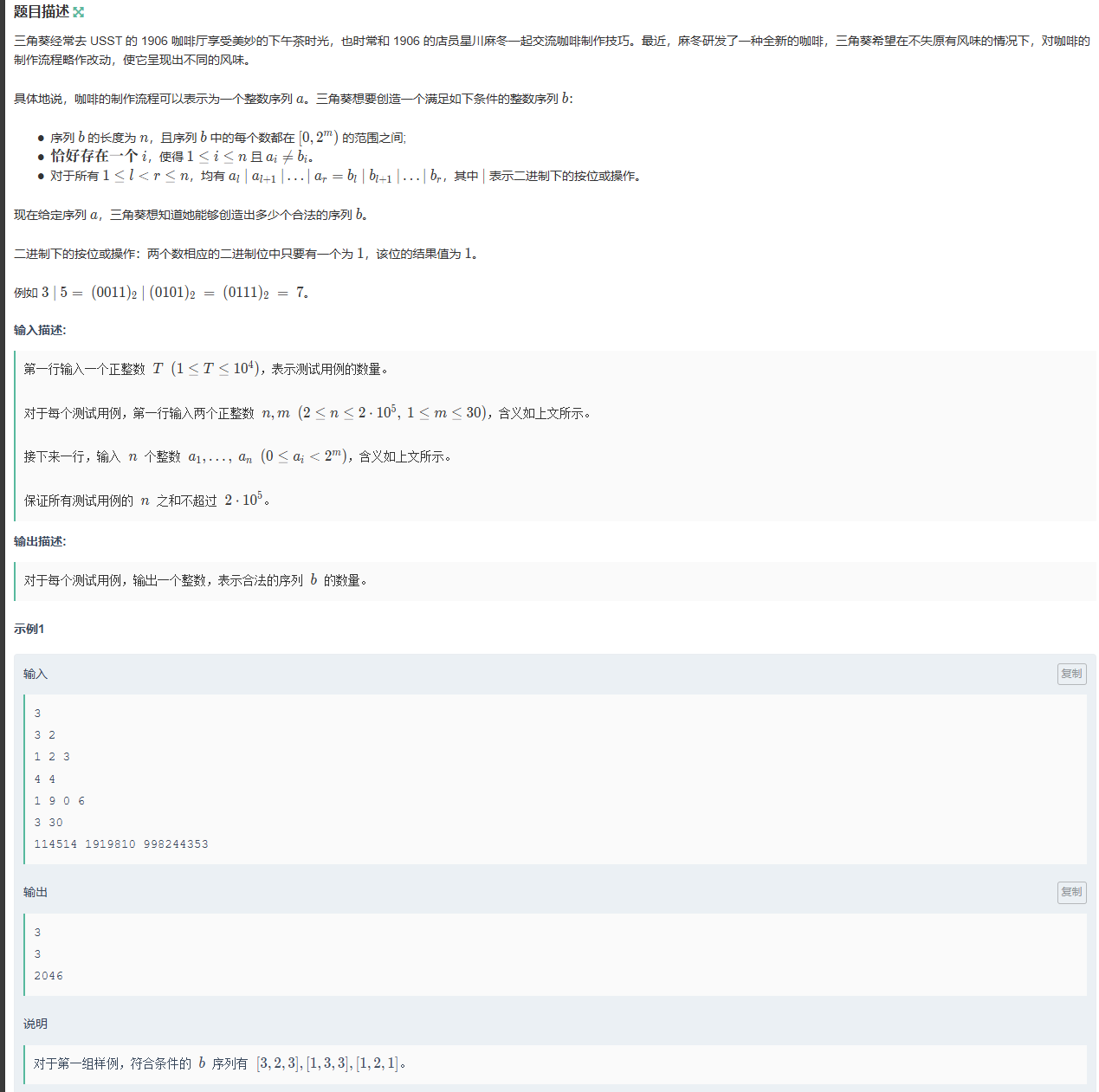
 本题的重点在于，改变一个数，使其与相邻的数或运算结果不变即可（需要特判1与n）

我们不需要遍历每一个rl，只要与相邻的运算结果不改变，就一定全局不变； 

这极大降低了运算的复杂性，只需要和旁边进行比较 

#include <bits/stdc++.h>
using namespace std;int a[200002]; // 存储每组测试用例的 a 序列int main() {// 加速 IO：关闭同步 + 解除 cin/cout 绑定，竞赛常用优化ios::sync_with_stdio(false);cin.tie(nullptr);int T; // 测试用例数量cin >> T;while (T--) { // 处理每组测试用例int n, m; // n: a 序列长度；m: 题目中 2^m 相关（虽未直接用，但输入需读）cin >> n >> m;// 读入 a 序列（下标从 1 开始，方便边界处理）for (int i = 1; i <= n; ++i) {cin >> a[i];}long long ans = 0; // 存储最终合法 b 序列数量// ========== 处理序列两端（i=1、i=n 附近） ==========// 1. 处理 a[1] 和 a[2] 的组合if (n >= 2) { // 至少有 2 个元素才需要处理int re_diff = a[2] & (~a[1]); // a2 有、a1 无的位（差异位候选）int re_same = a[2] & a[1];    // a2 和 a1 都有的位（相同位）int count = __builtin_popcount(re_diff) + __builtin_popcount(re_same);// 合法组合数：2^count - 1（所有位自由选，减去全不选的情况）ans += (1LL << count) - 1; }// 2. 处理 a[n-1] 和 a[n] 的组合（n>=2 时才会进入，否则 n-1 无意义）if (n >= 2) { int re_diff = a[n-1] & (~a[n]); // a[n-1] 有、a[n] 无的位int re_same = a[n-1] & a[n];    // a[n-1] 和 a[n] 都有的位int count = __builtin_popcount(re_diff) + __builtin_popcount(re_same);ans += (1LL << count) - 1; }// ========== 处理序列中间元素（2 <= i <= n-1） ==========for (int i = 2; i < n; ++i) { // 遍历中间每个位置 i// 左邻居 a[i-1]、右邻居 a[i+1] 与当前 a[i] 的关系int left_diff = a[i-1] & (~a[i]);  // a[i-1] 有、a[i] 无的位int right_diff = a[i+1] & (~a[i]); // a[i+1] 有、a[i] 无的位int same_both = left_diff & right_diff; // 左右都能“扩展”的差异位int left_same = a[i-1] & a[i];   // a[i-1] 和 a[i] 都有的位int right_same = a[i+1] & a[i];  // a[i+1] 和 a[i] 都有的位int same_common = left_same & right_same; // 左右都相同的位// 总共有多少位可以自由选择（差异位交集 + 相同位交集）int count = __builtin_popcount(same_both) + __builtin_popcount(same_common);// 合法组合数：2^count - 1ans += (1LL << count) - 1; }// 输出当前测试用例的结果cout << ans << '\n';}return 0;
}

例题2

 不改变所有条件，仅改变

使l,r为1-n;

此时，不能仅仅判断相邻位，需要与最终结果进行比较有多少位可以改变。 

#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false); // 加速输入输出cin.tie(nullptr);int T;cin >> T;while (T--) {int n, m, o = 0, p = 0; // o 用于记录前缀按位或，p 用于记录中间结果cin >> n >> m;vector<int> a(n);// 读取数组并计算前缀按位或结果for (int i = 0; i < n; ++i) {cin >> a[i];p = p | (o & a[i]);  // 计算中间结果 po = o | a[i];        // 更新前缀按位或结果}long long ans = 0;// 遍历每个位置，计算可能的合法序列数目for (int i = 0; i < n; ++i) {int result = o & (~a[i]);  // 计算o与a[i]的补码的按位与int count = __builtin_popcount(result);  // 统计结果中1的位数int ea = p & a[i];  // 计算p与a[i]的按位与count += __builtin_popcount(ea);  // 累加ea中1的位数// 合法序列数目为2^count -1（排除全0情况）ans += pow(2, count) - 1;}cout << ans << '\n';}return 0;
}