python学智能算法(二十三)|SVM-几何距离
引言
前序学习文章中,已经探究了电荷超平面的距离计算方法,相关文章为点与超平面的距离。
在这片文章中,我们了解到计算距离的公式:
F=mini=1...myi(w⋅xi+b)F=\min_{i=1...m}y_{i}(w\cdot x_{i}+b)F=i=1...mminyi(w⋅xi+b)
计算点与超平面的距离
对此,可以书写代码进行计算:
# 引入numpy模块
import numpy as np# 定义example_functional_margin()函数
def example_functional_margin(w,b,x,y):# 先对w和x两个参数执行点击运算,然后添加偏置量b后与y相乘result = y*(np.dot(w,x)+b)return result# 定义functional_margin()函数
def functional_margin_array(w,b,X,y):# 直接调用example_functional_margin()函数,按照枚举函数的顺序,逐个计算return np.array([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])# 定义functional_margin()函数
def functional_margin(w,b,X,y):# 直接调用example_functional_margin()函数,按照枚举函数的顺序,逐个计算return np.min([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])x=np.array([[1,1],[2,2]])
y=1b_1=5
w_1=np.array([2,1])w_2=w_1*10
b_2=b_1*10# 所有结果均输出
print(functional_margin_array(w_1,b_1,x,y))
print(functional_margin_array(w_2,b_2,x,y))
# 最小结果输出
print(functional_margin(w_1,b_1,x,y))
print(functional_margin(w_2,b_2,x,y))
代码运行效果为:

在上述代码中,我们会有一个发现:在向量x不改变的前提下,如果等比率调整权重向量w和偏置量b,获得的距离F也会等比率变化。而对于超平面计算公式w⋅x+b=0w\cdot x+b=0w⋅x+b=0
w和x无论扩大多少倍,公式依然成立。
因此,必须进一步修正点与超平面的计算公式,消除w和b按比率变化的影响。
点与超平面距离公式修正
在先前的学习进程中,通过向量的值和方向我们已经掌握方向向量的计算方法:
w=(w1∥w∥,w2∥w∥)w=(\frac{w_{1}}{\left \| w \right \|},\frac{w_{2}}{\left \| w \right \|})w=(∥w∥w1,∥w∥w2)由上式可知,方向向量是一个单位向量,一个向量无论放大多少倍,方向向量都不会改变。
因此,合理的点与超平面计算公式应当回归到将w转化为单位向量,使得所有计算基准统一,定义此时的距离为几何距离δ:δ=mini=1...myi(w∥w∥⋅x+b∥w∥)\delta =\min_{i=1...m}y_{i}(\frac{w}{\left \| w \right \|}\cdot x+\frac{b}{\left \| w \right \|})δ=i=1...mminyi(∥w∥w⋅x+∥w∥b)
δ的计算和F最大的不同在于:将权重向量统一为单位向量。
此时再次计算点与超平面的距离时就不用担心权重向量w和偏置量b的取值。
# 引入numpy模块
import numpy as np# 定义example_functional_margin()函数
def example_functional_margin(w,b,x,y):# 先对w和x两个参数执行点击运算,然后添加偏置量b后与y相乘result = y*(np.dot(w,x)+b)return result# 定义functional_margin()函数
def functional_margin_array(w,b,X,y):# 直接调用example_functional_margin()函数,按照枚举函数的顺序,逐个计算return np.array([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])# 定义functional_margin()函数
def functional_margin(w,b,X,y):# 直接调用example_functional_margin()函数,按照枚举函数的顺序,逐个计算return np.min([example_functional_margin(w,b,x,y)for i,x in enumerate(X)])x=np.array([[1,1],[2,2]])
y=1b_1=5
w_1=np.array([2,1])w_2=w_1*10
b_2=b_1*10# 所有结果均输出
print(functional_margin_array(w_1,b_1,x,y))
print(functional_margin_array(w_2,b_2,x,y))
# 最小结果输出
print(functional_margin(w_1,b_1,x,y))
print(functional_margin(w_2,b_2,x,y))# 将计算基准转化为权重矩阵的单位向量
def example_functional_margin_unit_ector(w,b,x,y):unit=np.linalg.norm(w)result=y*(np.dot(w/unit,x)+b/unit)return result# 计算基于单位向量的距离
def geometric_margin(w,b,X,y):return np.array([example_functional_margin_unit_ector(w,b,x,y)for i,x in enumerate(X)])# 输出单位向量基准的距离
print(geometric_margin(w_1,b_1,x,y))
print(geometric_margin(w_2,b_2,x,y))
此时的计算结果为:
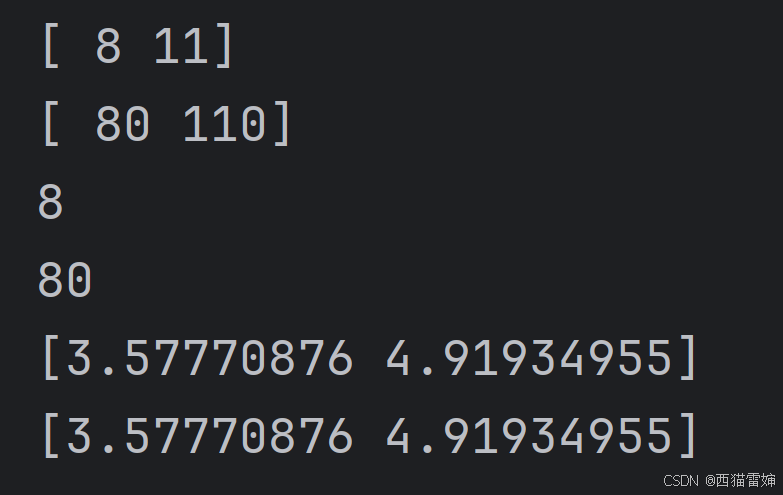
由计算效果可见,此时尽管w放大10倍,但计算获得的几何距离值不变。
总结
学习了几何距离的定义和计算。
