数学基础知识:三角函数
边的概念
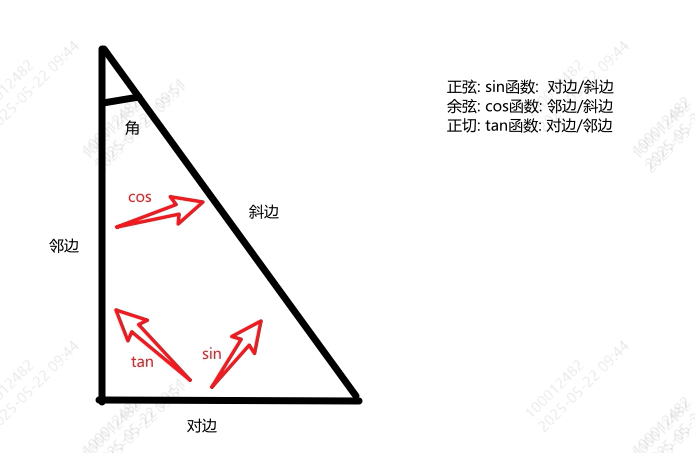
有一个直角三角形,找出一个锐角a
与角a相邻的是直角边是邻边;
与角a相对的直接边是对边;
与直角相对的边是斜边;
函数定义
正弦: sin函数 : 对边/斜边
余弦: cos函数: 邻边/斜边
正切: tan函数: 对边/邻边
图例如下
三角函数与圆的关系:
其实三角函数也称圆函数,三角函数和圆有着直接的关系
草图示例:
这是本人画的一个草图,虽有些潦草,但是也够看了....
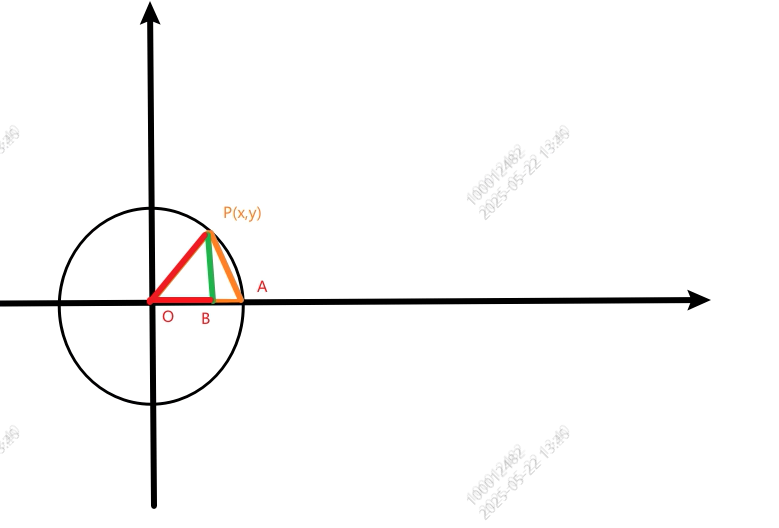
过程:
在坐标轴上,以坐标(0,0)为圆点O,画一个半径为1的圆。
线段OA作为圆上的一个半径,长度为1
现在以OA线段为始边,OP为终边,绘制一个夹角POA。P点的坐标将其定义为(x,y)
画出△OAP的垂直线,也就是PB,形成一个△OBP
∠POB的正弦函数(sin) = 对边/斜边 = PB/PO = PB/1 = y
∠POB的余切函数(cos) = 邻边/斜边 = OB/PO = OB/1 = x
∠POB的正切函数(tan) = 对边/邻边 = PB/OB = y/x
结论:
三角形与圆上的P点(x,y)的关系
sinθ = y
cosθ = x
tanθ = y/x (x≠0)
三角函数图解
正弦图解:
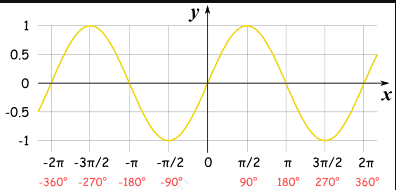
图像特征:
- 周期为2π(或者360°,即圆)
- 上下振幅为1,也就是圆的半径为1
- 值在[-1,1]之间波动
规律:
θ(读作西塔,代表角度),在图中就是x轴的值,对应的三角函数值就是y轴的值
- θ=0: sin0 = 0
- θ=π/2(90°): sinπ/2 = 1
- θ=π(180°): sinπ = 0
- θ=3/2π(270°): sin3/2π = -1
- θ=2π(360°): sin2π = 0
余弦图解:
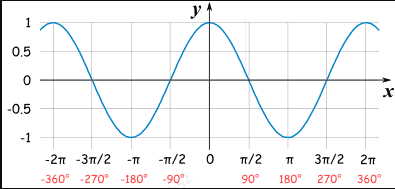
图像特征:
- 周期为2π
- 振幅为1
- 图像在[-1,1]之间波动
规律:
- θ=0: cos0 = 1
- θ = π/2(90°): cosπ/2 =0
- θ = π(180°): cosπ=1
- θ = 3/2π(270°): cos3/2π = 0
- θ = 2π(360°): cos2π = 1
余切图解:
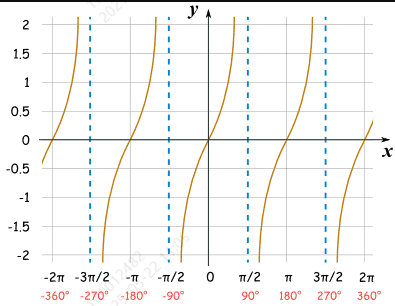
图像特征:
k是整数
- 周期为π,或者90°
- 图像在θ = π/2 + kπ处有垂直渐进线
- 在每个周期内,函数从负无穷增加到正无穷
规律:
- θ =0: tan0 = 0
- θ = π/4(45°): tanπ/4 = 1
- θ = π/2: 垂直渐近线
- θ = 3/4π(135°): tan3/4π = -1
- θ = π(180°): tanπ = 0
反三角函数
三角函数可以根据角度求边的比例,如果知道具体的边长,可以根据反三角函数去求的角度的大小
用正弦函数举例子:
sin(角度) = (对边/斜边)
比如: sin30° = 1/2

arcsin(对边/斜边) = 角度
假如现在一个对边/斜边的角度为1/2,求角度
arcsin(1/2) = 30°

arcsin也可以写成上面那种写法,在计算器中看到sin^-1就是arcsin,余弦和正切同样如此
倒余弦函数和倒正切函数同样如此
关系比
倒数关系
csc代表余割, sec代表正割,cot代表余切
- cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
平方比
- sin^2θ+cos^2θ=1
- 1+tan^2θ=sec^2θ
- 1+cot^2θ=csc^2θ
和角公式
- sin(α±β)=sinαcosβ±cosαsinβ
- cos(α±β)=cosαcosβ∓sinαsinβ
- tan(α±β)=1∓tanαtanβtanα±tanβ
实际应用
已知一个三角形的两条边的长度和这两条边形成的夹角,求知该三角形所有边的长度和所有内角的度数
思路:
1.绘制图形
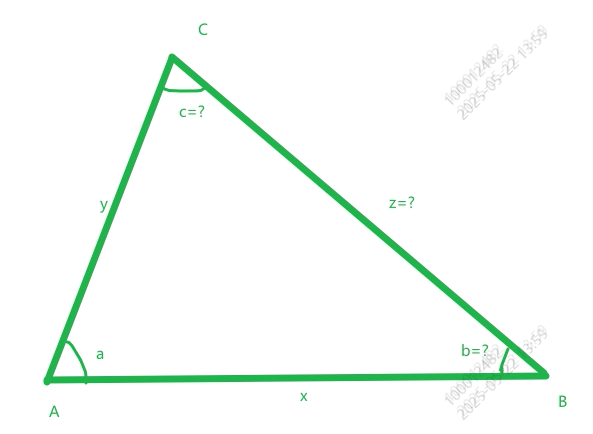
已知角a和线段x,y的值,求角b角c和对边z的值
2.画垂直辅助线CP,求长度
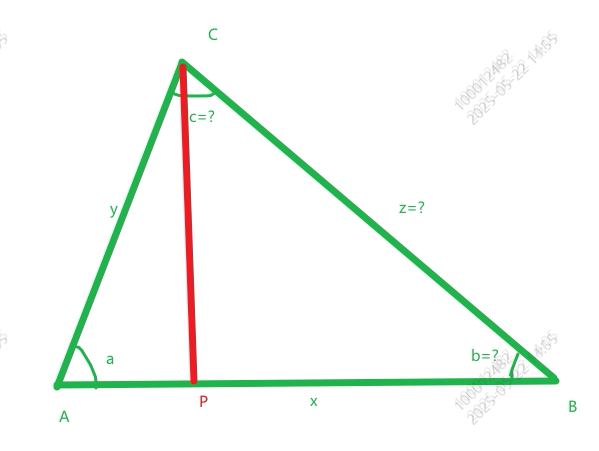
已知角a的大小,就可以直接算出cos a的大小
角a的余弦: cos a = 对边/斜边 = CP/y
CP = cos a * y
根据勾股定理: 斜边AC的平方 = 直角边AP的平方+直角边CP的平方
求得AP = √ ̄(y^2-CP^2)
这样的话,CP和AP我们都求到了
直角△ PCB的斜边就可以算出来了
z = √ ̄((x-AP)^2+CP^2)
未知边z的值就计算出来了
现在已知斜边z和对边CP的长度,根据反正弦函数arcsin求得角度b
b = arcsin(CP/z)
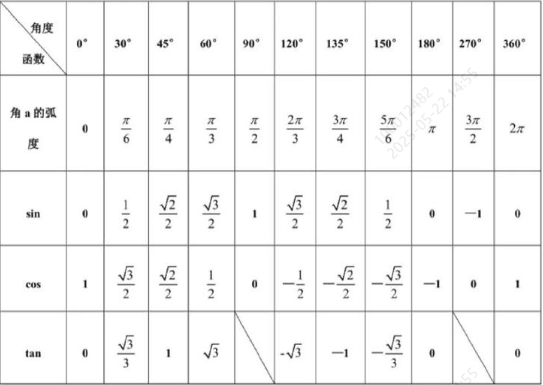
三角函数常用角度比例: