机器学习+多目标优化的算法如何设计?
一、核心问题与设计思路
机器学习(ML)与多目标优化(MOO)的结合旨在解决两类核心问题:
- 利用ML提升MOO算法的性能:通过机器学习模型预测解的质量、优化搜索方向或加速收敛;
- 利用MOO优化ML模型的多目标冲突:例如平衡模型复杂度与准确性、特征数量与信息量等。
二、关键设计方向与算法框架
1. 基于分解的多目标优化(MOEA/D)与ML的结合
- 核心思想:将多目标问题分解为多个单目标子问题,每个子问题通过ML模型(如神经网络、SVM)预测局部最优解。
- 设计步骤:
- 分解策略:使用切比雪夫法、加权和法等将目标函数分解为子问题;
- 模型训练:利用历史解集训练ML模型,预测子问题的候选解;
- 动态更新:根据模型预测结果动态调整子问题的权重和邻域关系。
- 优势:降低计算复杂度(从O(MN³)降至O(MN²)),适用于高维目标空间。
2. 基于帕累托支配的进化算法(NSGA-II)与ML的融合
- 改进点:
- 非支配排序加速:使用ML分类器(如决策树)快速筛选非支配解,替代传统的O(MN²)排序;
- 拥挤距离优化:通过聚类算法(如K-means)辅助生成分布均匀的解集。
- 应用案例:在智能建筑能耗优化中,NSGA-II与支持向量机(SVM)结合,预测能耗与舒适度的帕累托前沿。
3. 强化学习(RL)与多目标优化的动态交互
- 框架设计:
- 状态表示:将目标函数值、约束条件编码为状态向量;
- 奖励机制:基于帕累托改进设计多目标奖励函数;
- 策略网络:使用深度Q网络(DQN)选择优化动作(如交叉、变异)。
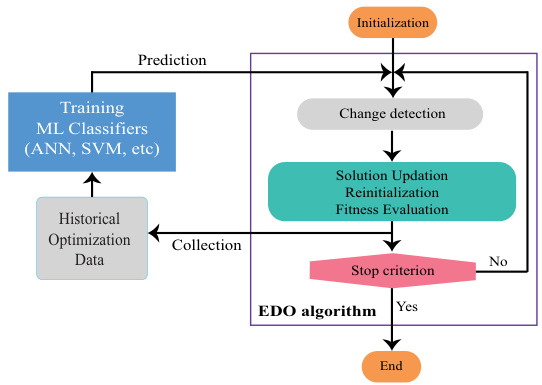
- 案例:在医疗决策中,RL代理通过交互式学习医生偏好,生成个性化治疗方案。
4. 多任务学习与梯度下降的结合
- 数学形式:
min θ ∑ i = 1 k λ i L i ( θ ) + Ω ( θ ) \min_{\theta} \sum_{i=1}^k \lambda_i L_i(\theta) + \Omega(\theta) θmini=1∑kλiLi(θ)+Ω(θ)
其中 λ i \lambda_i λi为动态权重,通过MOO算法优化。 - 算法改进:
- 多目标梯度下降:利用Barzilai-Borwein方法平衡不同任务的梯度方向;
- 自适应权重:通过进化算法动态调整 λ i \lambda_i λi,避免局部最优。
三、典型算法框架设计示例
框架:协同进化-机器学习集成(CoMAC-ML)
- 种群划分:
- 种群1:处理主要目标(如模型准确性);
- 种群2:处理辅助目标(如特征稀疏性)。
- 知识迁移:
- 使用迁移学习模型(如LSTM)提取种群间的共享特征;
- 通过MOEA/D分解策略生成混合解。
- 动态约束:
- 利用逻辑回归预测约束违反程度,动态调整可行域边界。
四、实际应用案例
- 智能建筑能耗优化:
- 方法:结合BIM数据与NSGA-II,利用随机森林预测能耗,生成帕累托最优解集;
- 结果:能耗降低15%,舒适度提升20%。
- 农业机械任务分配:
- 算法:改进的INSGA-II结合反向传播神经网络(BPNN)优化路径规划;
- 效果:能源消耗减少4.35%,任务完成时间缩短4.51%。
- 医疗多目标决策:
- 框架:交互式MOO系统,通过决策树学习医生偏好,生成治疗方案帕累托前沿。
五、挑战与解决方案
| 挑战 | 解决方案 |
|---|---|
| 计算复杂度高 | 使用ML模型(如LightGBM)预筛选解,减少目标函数评估次数 |
| 目标间不平衡性 | 引入Barzilai-Borwein梯度修正,动态调整目标权重 |
| 高维决策空间 | 采用特征选择(MOEA/DD)+ 自编码器降维 |
| 动态环境适应 | 集成LSTM预测环境变化,触发种群重置 |
| 可解释性不足 | 结合规则提取(如决策树)解释帕累托解 |
六、设计流程总结
- 问题定义:明确ML模型的多目标冲突(如精度 vs 速度);
- 算法选择:
- 小规模问题:MOEA/D + 线性模型;
- 大规模问题:NSGA-III + 深度学习;
- 交互机制:设计基于强化学习的动态权重调整策略;
- 评估指标:采用超体积(HV)、间距(Spacing)等帕累托前沿质量指标。
七、未来研究方向
- 量子多目标优化:结合量子退火算法与ML,突破经典计算瓶颈;
- 神经架构搜索(NAS) :用MOO自动平衡CNN的深度、参数量与推理速度;
- 联邦学习优化:在隐私保护约束下,联合优化模型精度与通信成本。
