GESP2024年9月认证C++八级( 第三部分编程题（2）美丽路径）

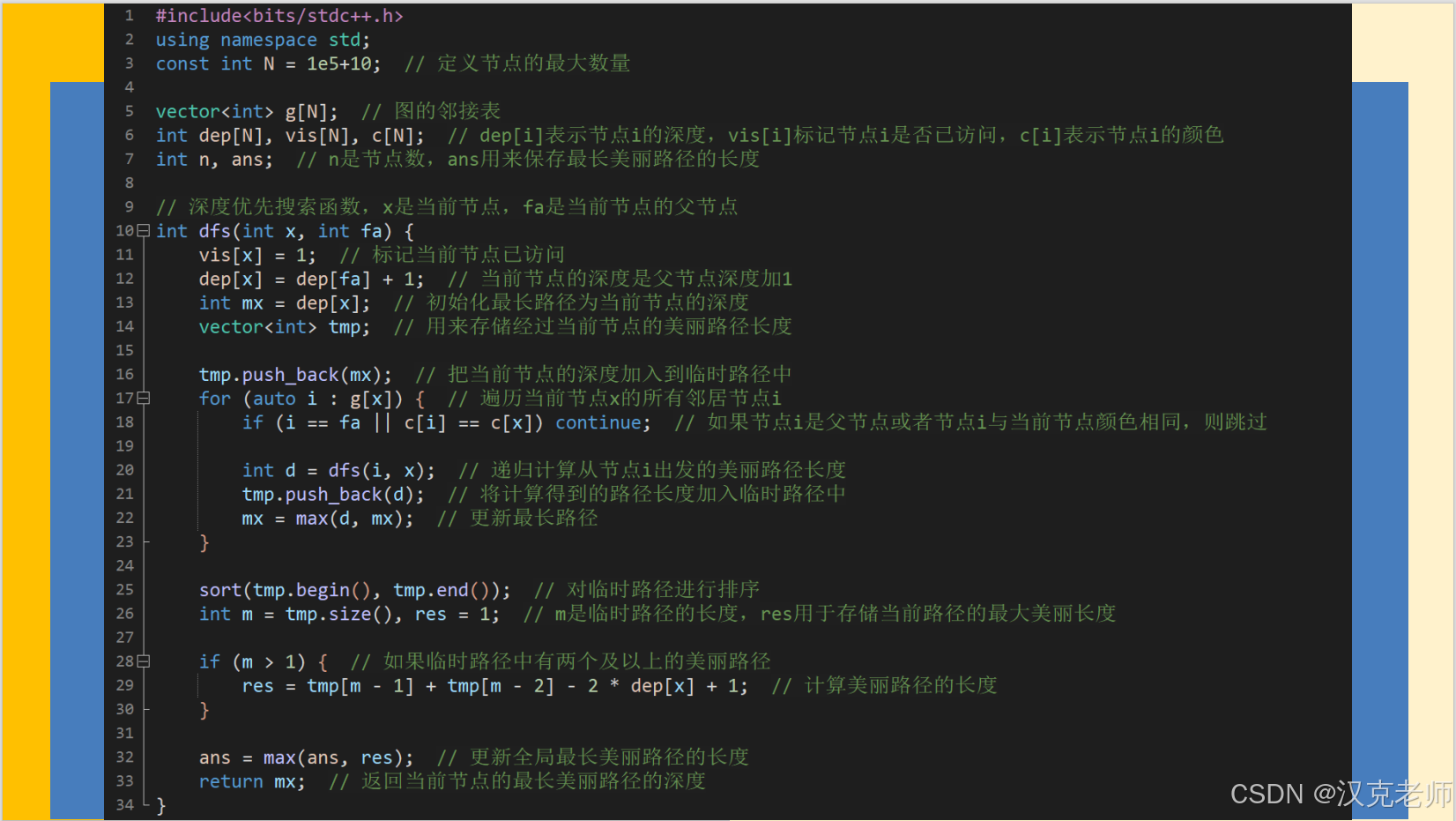
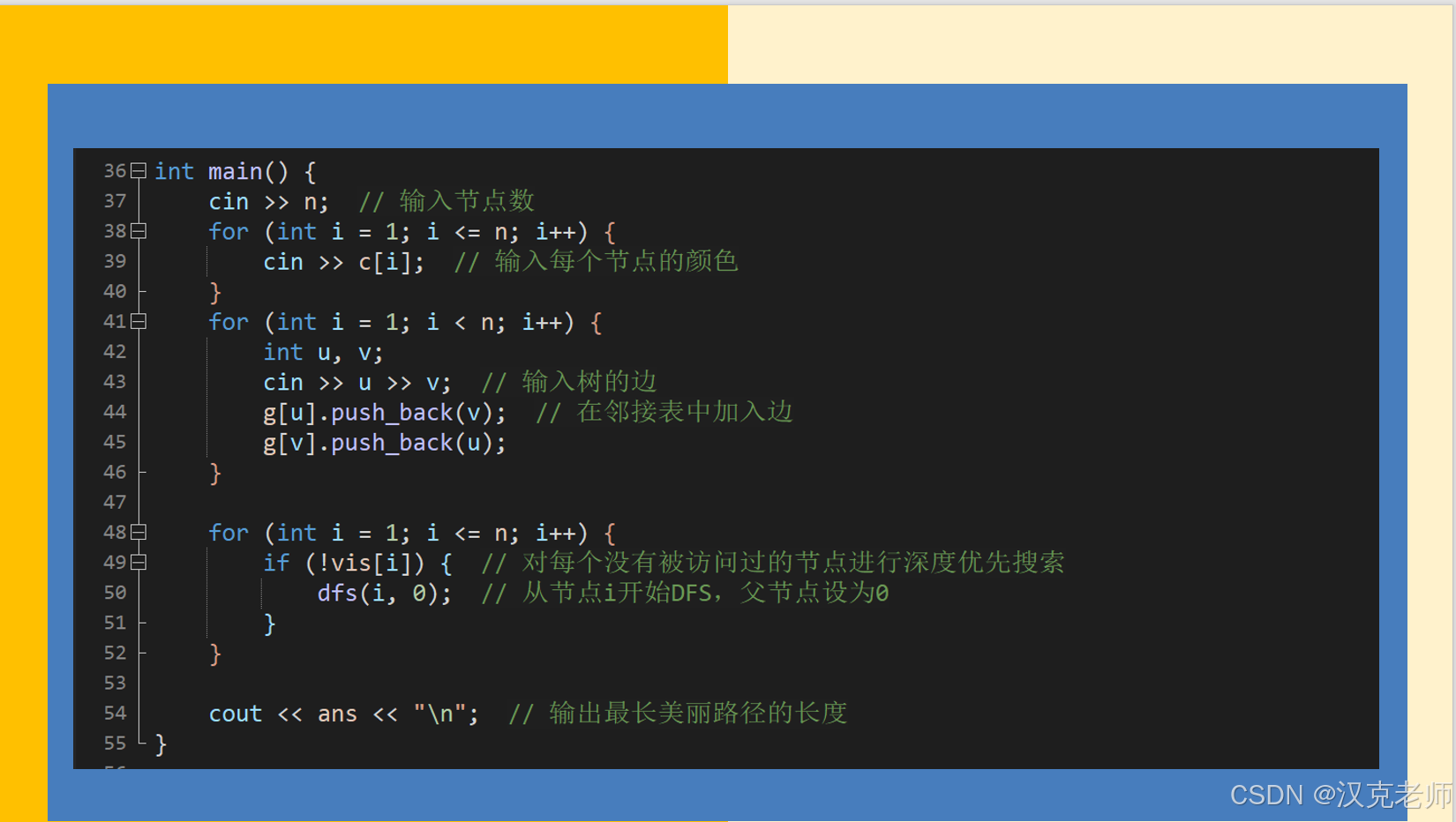
参考程序：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;  // 定义节点的最大数量vector<int> g[N];  // 图的邻接表
int dep[N], vis[N], c[N];  // dep[i]表示节点i的深度，vis[i]标记节点i是否已访问，c[i]表示节点i的颜色
int n, ans;  // n是节点数，ans用来保存最长美丽路径的长度// 深度优先搜索函数，x是当前节点，fa是当前节点的父节点
int dfs(int x, int fa) {vis[x] = 1;  // 标记当前节点已访问dep[x] = dep[fa] + 1;  // 当前节点的深度是父节点深度加1int mx = dep[x];  // 初始化最长路径为当前节点的深度vector<int> tmp;  // 用来存储经过当前节点的美丽路径长度tmp.push_back(mx);  // 把当前节点的深度加入到临时路径中for (auto i : g[x]) {  // 遍历当前节点x的所有邻居节点iif (i == fa || c[i] == c[x]) continue;  // 如果节点i是父节点或者节点i与当前节点颜色相同，则跳过int d = dfs(i, x);  // 递归计算从节点i出发的美丽路径长度tmp.push_back(d);  // 将计算得到的路径长度加入临时路径中mx = max(d, mx);  // 更新最长路径}sort(tmp.begin(), tmp.end());  // 对临时路径进行排序int m = tmp.size(), res = 1;  // m是临时路径的长度，res用于存储当前路径的最大美丽长度if (m > 1) {  // 如果临时路径中有两个及以上的美丽路径res = tmp[m - 1] + tmp[m - 2] - 2 * dep[x] + 1;  // 计算美丽路径的长度}ans = max(ans, res);  // 更新全局最长美丽路径的长度return mx;  // 返回当前节点的最长美丽路径的深度
}int main() {cin >> n;  // 输入节点数for (int i = 1; i <= n; i++) {cin >> c[i];  // 输入每个节点的颜色}for (int i = 1; i < n; i++) {int u, v;cin >> u >> v;  // 输入树的边g[u].push_back(v);  // 在邻接表中加入边g[v].push_back(u);}for (int i = 1; i <= n; i++) {if (!vis[i]) {  // 对每个没有被访问过的节点进行深度优先搜索dfs(i, 0);  // 从节点i开始DFS，父节点设为0}}cout << ans << "\n";  // 输出最长美丽路径的长度
}