当前位置： 首页 > java >正文

DAY-16-数组的常见操作和形状-2025.8.28

java 2025/8/29 15:30:02

数组的常见操作和形状

因为前天说了shap，这里涉及到数据形状尺寸问题，所以需要在这一节说清楚，后续的神经网络我们将要和他天天打交道。
知识点：
1.numpy数组的创建：简单创建、随机创建、遍历、运算
2.numpy数组的索引：一维、二维、三维
3.SHAP值的深入理解

作业：今日知识点比较多，好好记忆下

笔记：

1. NumPy 数组基础笔记

1. 理解数组的维度 (Dimensions)

NumPy 数组的维度 (Dimension) 或称为 轴 (Axis) 的概念，与我们日常理解的维度非常相似。

  • 直观判断: 数组的维度层数通常可以通过打印输出时中括号 [] 的嵌套层数来初步确定：
    • 一层 []: 一维 (1D) 数组。
    • 两层 []: 二维 (2D) 数组。
    • 三层 []: 三维 (3D) 数组，依此类推。

2. NumPy 数组与深度学习 Tensor 的关系

在后续进行频繁的数学运算时，尤其是在深度学习领域，对 NumPy 数组的理解非常有帮助，因为 PyTorch 或 TensorFlow 中的 Tensor 张量本质上可以视为支持 GPU 加速和自动微分的 NumPy 数组。掌握 NumPy 的基本操作，能极大地降低学习 Tensor 的门槛。关于 NumPy 更深入的性质，我们留待后续探讨。

3. 一维数组 (1D Array)

一维数组在结构上与 Python 中的列表（List）非常相似。它们的主要区别在于：

  • 打印输出格式: 当使用 print() 函数输出时：

    • NumPy 一维数组的元素之间默认使用空格分隔。

    • Python 列表的元素之间使用逗号分隔。

    • 示例 (一维数组输出):

      [7 5 3 9]

4. 二维数组 (2D Array)

二维数组可以被看作是“数组的数组”或者一个矩阵。其结构由两个主要维度决定：

  • 行数: 代表整个二维数组中包含多少个一维数组。
  • 列数: 代表每个一维数组（也就是每一行）中包含多少个元素。

值得注意的是，二维数组不一定是正方形（即行数等于列数），它可以是任意的 n * m 形状，其中 n 是行数，m 是列数。

5. 数组的创建

NumPy 的 array() 函数非常灵活，可以接受各种“序列型”对象作为输入参数来创建数组。这意味着你可以将 Python 的列表 (List)、元组 (Tuple)，甚至其他的 NumPy 数组等数据结构直接传递给 np.array() 来创建新的 NumPy 数组。

2. 数组的简单创建

import numpy as np
a = np.array([2,4,6,8,10,12])  # 创建一个一维数组
b = np.array([[2,4,6],[8,10,12]])  # 创建一个二维数组
print(a,'\n',b)# 分清楚列表和数组的区别
print([7, 5, 3, 9])  # 输出: [7, 5, 3, 9]（逗号分隔）是列表
print(np.array([7, 5, 3, 9]))  # 输出: [7 5 3 9]（空格分隔） 是数组

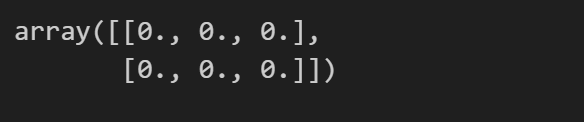
在这里插入图片描述

zeros = np.zeros((2,3)) # 创建一个2行3列的全零矩阵
zeros

在这里插入图片描述

ones = np.ones((3,)) # 创建一个形状为(3,)的全1数组
ones

在这里插入图片描述

# 顺序数组的创建
arange = np.arange(1,10) # 创建一个从1到10的数组
arange

在这里插入图片描述

1. 数组的随机化创建

  1. 在后续深度学习中，我们经常需要对数据进行随机化处理，以确保模型的泛化能力。
  2. 为了测试很多函数的性能，往往需要随机化生成很多数据。
  • NumPy随机数生成方法对比
方法作用范围/分布记忆口诀典型应用场景示例
np.random.randint(a,b)[a,b]整数"int"结尾表示整数生成随机索引/标签np.random.randint(1,10) → 7
random.random()[0,1)浮点数纯"random"最基础简单概率模拟random.random() → 0.548
np.random.rand()[0,1)均匀分布“rand”=random+uniform蒙特卡洛模拟np.random.rand(3) → [0.2,0.5,0.8]
np.random.randn()标准正态分布(μ=0,σ=1)多一个"n"=normal数据标准化/深度学习初始化np.random.randn(2,2) → [[-0.1,1.2],[0.5,-0.3]]
  • 记忆技巧：

  1. 看结尾：

    • “int” → 整数
    • “n” → 正态(normal)

  2. 看前缀：

    • 纯"random" → Python基础随机
    • “np.random” → NumPy增强版

  3. 功能差异：

    • rand()和random()都是均匀分布，但rand()能直接生成数组
    • randn()生成的数据会有正有负，其他方法都是非负数
# 创建一个2*2的随机数组c，区间为[0,1)
c = np.random.rand(2,2)
c

在这里插入图片描述

import numpy as np
np.random.seed(42) # 设置随机种子以确保结果可以复现# 生成10个语文成绩（正态分布，均值75，标准差10）
chinese_scores = np.random.normal(75,10,10).round(1)# 找出最高分和最低分及其索引
max_score = np.max(chinese_scores)
max_index = np.argmax(chinese_scores)
min_score = np .min(chinese_scores)
min_index = np.argmin(chinese_scores)print(f'''
所有成绩：{chinese_scores}
最高分：{max_score}(第{max_index}个学生)
最低分：{min_score}(第{min_index}个学生)
''')

在这里插入图片描述

import numpy as np
scores = np.array([5,9,9,11,11,13,15,19])
scores += 1 # 学习一下这个写法，等价于 scores = scores + 1
sum = 0
for i in scores:sum += i
print(sum)

在这里插入图片描述

2. 数组的运算

  1. 矩阵乘法：需要满足第一个矩阵的列数等于第二个矩阵的行数，和线代的矩阵乘法算法相同。
  2. 矩阵点乘：需要满足两个矩阵的行数和列数相同，然后两个矩阵对应位置的元素相乘。
  3. 矩阵转置：将矩阵的行和列互换。
  4. 矩阵求逆：需要满足矩阵是方阵且行列式不为0，然后使用伴随矩阵除以行列式得到逆矩阵。
  5. 矩阵求行列式：需要满足矩阵是方阵，然后使用代数余子式展开计算行列式。
import numpy as np
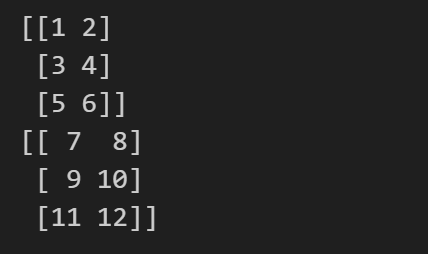
a = np.array([[1, 2], [3, 4], [5, 6]])
b = np.array([[7, 8], [9, 10], [11, 12]])
print(a)
print(b)

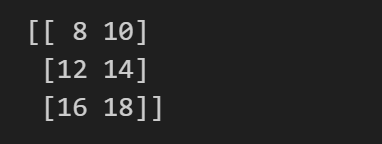
在这里插入图片描述

print(a + b) # 计算两个数组的和

在这里插入图片描述

print(a - b) # 计算两个数组的差

在这里插入图片描述

print(a / b) # 计算两个数组的除法

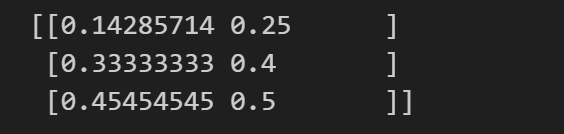
在这里插入图片描述

a * b # 矩阵点乘，ipynb文件中不使用print()函数会自动输出结果，这是ipynb文件的特性

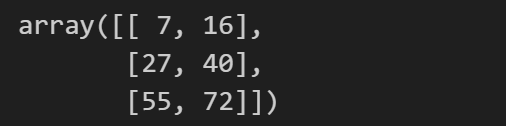
在这里插入图片描述

a @ b.T # 矩阵乘法,3*2的矩阵和2*3的矩阵相乘，得到3*3的矩阵

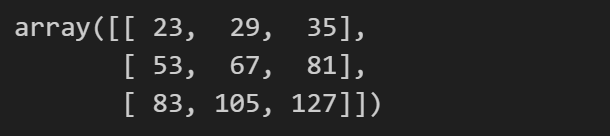
在这里插入图片描述

3. 数组的索引

1. 一维数组索引

arrid = np.arange(10)
arrid

在这里插入图片描述

# 1. 取出数组的第一个元素。
arr1d[0]  # 0

# 取出数组的最后一个元素。-1表示倒数第一个元素。
arr1d[-1] # 9 

# 3. 取出数组中索引为 3, 5, 8 的元素。
# 使用整数数组进行索引，可以一次性取出多个元素。语法是 arr1d[[index1, index2, ...]]。
arr1d[[3, 5, 8]]  # array([3,5,8])

# 切片取出索引
arr1d[2:6] # 取出索引为2到5的元素（不包括索引6的元素，取左不取右）# array([2, 3, 4, 5])

# 取出数组中从头到索引 5 (不包含 5) 的元素。
# 使用切片 slice [:stop]
arr1d[:5]# array([0, 1, 2, 3, 4])

# 取出数组中从索引 4 到结尾的元素。
# 使用切片 slice [start:]
arr1d[4:]# array([4, 5, 6, 7, 8, 9])

# 取出全部元素
arr1d[:]# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 7取出数组中所有偶数索引对应的元素 (即索引 0, 2, 4, 6, 8)。
# 使用带步长的切片 slice [start:stop:step]
arr1d[::2]# array([0, 2, 4, 6, 8])

2. 二维数组索引

# 数组:
arr2d = np.array([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12],[13, 14, 15, 16]])
arr2d

在这里插入图片描述
索引顺序：在二维数组 arr2d 里，第一个索引值代表行，第二个索引值代表列。比如 arr2d[i, j] ，i 是行索引，j 是列索引。

# 取出第 1 行 (索引为 1) 的所有元素。
#
# 使用索引 arr[row_index, :] 或 arr[row_index]
arr2d[1, :]# array([5, 6, 7, 8])

# 也可以省略后面的 :
arr2d[1]# array([5, 6, 7, 8])

# 取出第 2 列 (索引为 2) 的所有元素。
# 使用索引 arr[:, column_index]
arr2d[:, 2]# array([ 3,  7, 11, 15])

# 取出位于第 2 行 (索引 2)、第 3 列 (索引 3) 的元素。
# 使用 arr[row_index, column_index]
arr2d[2, 3]# 12

# 取出由第 0 行和第 2 行组成的新数组。
# 使用整数数组作为行索引 arr[[row1, row2, ...], :]
arr2d[[0, 2], :]# array([[ 1,  2,  3,  4],[ 9, 10, 11, 12]])

# 取出由第 1 列和第 3 列组成的新数组。
# 使用整数数组作为列索引 arr[:, [col1, col2, ...]]
arr2d[:, [1, 3]]# array([[ 2,  4],
#        [ 6,  8],
#        [10, 12],
#        [14, 16]])

# 取出一个 2x2 的子矩阵，包含元素 6, 7, 10, 11。
# 使用切片 slice arr[row_start:row_stop, col_start:col_stop]
arr2d[1:3, 1:3]# array([[ 6,  7],
#        [10, 11]])

3. 三维数组索引

arr3d = np.arange(3 * 4 * 5).reshape((3, 4, 5))
arr3d

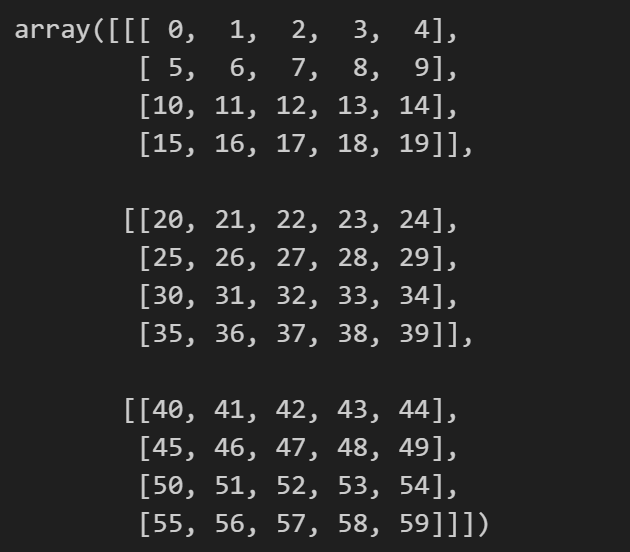
在这里插入图片描述

# 选择特定的层
# 使用整数数组 [0, 2] 作为第一个维度 (层) 的索引
arr3d[1, :, :]

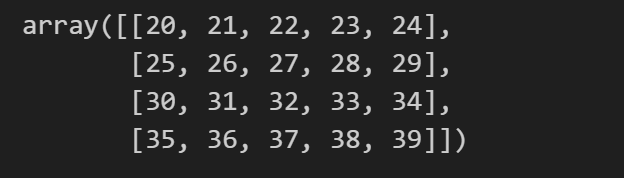
在这里插入图片描述

arr3d[1, 0:2, :]

在这里插入图片描述

arr3d[1, 0:2, 2:4]

在这里插入图片描述

总结

一、NumPy 数组的创建与操作

1. 数组的简单创建
NumPy 数组（ndarray）是同构数据的多维容器，创建方式主要有：

  • 从 Python 列表转换： 通过np.array()将列表或嵌套列表转换为数组
  • 特殊数组生成： zeros（全 0）、ones（全 1）、arange（序列）、linspace（均分序列）、eye（单位矩阵）等
import numpy as np# 从列表创建
arr1 = np.array([1, 2, 3, 4])  # 一维数组
arr2 = np.array([[1, 2], [3, 4]])  # 二维数组（2x2）# 特殊数组
zeros_arr = np.zeros((2, 3))  # 2行3列全0数组
ones_arr = np.ones((3, 2))   # 3行2列全1数组
range_arr = np.arange(0, 10, 2)  # 0到10（不包含），步长2 → [0,2,4,6,8]
linspace_arr = np.linspace(0, 1, 5)  # 0到1均分5个点 → [0,0.25,0.5,0.75,1]
eye_arr = np.eye(3)  # 3x3单位矩阵（对角线为1，其余为0）

2. 随机数组创建
通过np.random模块生成随机数组，常用函数：

  • rand：均匀分布（0-1）
  • randn：标准正态分布（均值 0，方差 1）
  • randint：整数随机分布
# 均匀分布（2行3列，值∈[0,1)）
rand_arr = np.random.rand(2, 3)  # 标准正态分布（3行2列）
randn_arr = np.random.randn(3, 2)  # 整数随机（10-20之间，生成4个整数）
randint_arr = np.random.randint(10, 20, size=4)  # 固定随机种子（保证结果可复现）
np.random.seed(42)  # 种子固定后，后续随机结果一致

3. 数组的遍历
遍历方式取决于数组维度，多维数组可通过嵌套循环或np.nditer高效遍历：

# 一维数组遍历
arr1 = np.array([1, 2, 3])
for x in arr1:print(x)  # 1 → 2 → 3# 二维数组遍历（行→列）
arr2 = np.array([[1, 2], [3, 4]])
for row in arr2:for x in row:print(x)  # 1 → 2 → 3 → 4# 高效遍历（nditer）
for x in np.nditer(arr2):print(x)  # 1 → 2 → 3 → 4（按内存顺序）

4. 数组的运算
NumPy 支持元素级运算和矩阵运算，无需循环，效率极高：

  • 元素级运算：±*/、幂运算（**）等，自动广播（不同形状数组兼容时）
  • 矩阵运算：矩阵乘法（np.dot()或@）、转置（.T）
  • 聚合运算：sum、mean、max等（可指定轴axis）
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])# 元素级运算
print(a + b)  # [5,7,9]
print(a * 2)  # [2,4,6]
print(a **2)  # [1,4,9]# 矩阵乘法（2x3矩阵 × 3x2矩阵 → 2x2矩阵）
c = np.array([[1, 2, 3], [4, 5, 6]])  # 2x3
d = np.array([[1, 2], [3, 4], [5, 6]])  # 3x2
print(np.dot(c, d))  # 等价于 c @ d → [[22, 28], [49, 64]]# 聚合运算（按轴计算）
e = np.array([[1, 2], [3, 4]])
print(e.sum())  # 10（所有元素和）
print(e.sum(axis=0))  # [4,6]（按列求和）
print(e.mean(axis=1))  # [1.5, 3.5]（按行求均值）

二、NumPy 数组的索引

索引用于获取数组中的元素，核心是通过[]指定维度位置，语法随维度增加而扩展。
1. 一维数组索引
与 Python 列表索引一致，支持基本索引（单个元素）和切片（连续元素）：

arr = np.array([10, 20, 30, 40, 50])# 基本索引（获取单个元素，从0开始）
print(arr[0])  # 10
print(arr[-1])  # 50（最后一个元素）# 切片（[start:end:step]，左闭右开）
print(arr[1:4])  # [20,30,40]（索引1到3）
print(arr[::2])  # [10,30,50]（步长2，间隔取元素）

2. 二维数组索引
语法：arr[row_index, col_index]（注意用逗号分隔行和列，而非arr[row][col]，后者效率低）。

arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]
])  # 3x3矩阵# 获取单个元素（第2行第3列，索引从0开始）
print(arr[1, 2])  # 6# 切片（行切片 + 列切片）
print(arr[0:2, 1:3])  # 取前2行，后2列 → [[2,3], [5,6]]# 取整行/整列
print(arr[1, :])  # [4,5,6]（第2行所有列）
print(arr[:, 2])  # [3,6,9]（第3列所有行）

3. 三维数组索引
三维数组可理解为 “层→行→列”，语法：arr[layer_index, row_index, col_index]。

# 2层 × 2行 × 3列的三维数组
arr = np.array([[[1, 2, 3], [4, 5, 6]],  # 第0层[[7, 8, 9], [10, 11, 12]]  # 第1层
])# 获取单个元素（第1层，第1行，第2列）
print(arr[1, 1, 2])  # 12# 切片（取第0层的所有行，前2列）
print(arr[0, :, 0:2])  # [[1,2], [4,5]]# 取所有层的第0行
print(arr[:, 0, :])  # [[1,2,3], [7,8,9]]

三、SHAP 值的深入理解

SHAP（SHapley Additive exPlanations）是一种基于博弈论的模型解释方法，用于量化每个特征对模型预测结果的贡献，核心是解决 “如何公平分配每个特征的重要性” 问题。

1. 核心思想

SHAP 值源于博弈论中的Shapley 值：在一个合作博弈中，每个参与者（特征）的贡献等于其在所有可能 “联盟”（特征子集）中的边际贡献的平均值。

对于机器学习模型，“博弈” 的目标是预测结果，“参与者” 是输入特征，“联盟” 是特征的子集。某特征的 SHAP 值表示：该特征对预测结果的平均边际贡献（相对于所有其他特征的组合）。

2. 数学定义

在这里插入图片描述

3. 关键性质

在这里插入图片描述

4. 优势与应用

  • 可解释性强：直接量化每个特征对单个预测的贡献（正值表示促进预测，负值表示抑制）。
  • 通用性：适用于任何模型（树模型、神经网络、线性模型等）。
  • 应用场景：特征重要性分析、异常预测解释、模型偏见检测等。

5. 实际计算
在这里插入图片描述

import shap
import sklearn.ensemble# 训练一个随机森林模型
X, y = shap.datasets.diabetes()
model = sklearn.ensemble.RandomForestRegressor()
model.fit(X, y)# 初始化解释器（TreeSHAP针对树模型）
explainer = shap.TreeExplainer(model)
# 计算前10个样本的SHAP值
shap_values = explainer.shap_values(X[:10])# 可视化（Force Plot展示单个预测的特征贡献）
shap.force_plot(explainer.expected_value, shap_values[0], X[0])

总结：SHAP 值通过博弈论框架解决了特征重要性的 “公平分配” 问题，是目前最强大的模型解释工具之一，尤其适合需要高可信度解释的场景（如医疗、金融）。

@浙大疏锦行

http://www.xdnf.cn/news/19040.html

相关文章：

  • FISCO-BCOS-Python 模板
  • RAG概念被误用：AI应用落地需回归上下文工程本质
  • 解锁AI“黑匣”：监督、无监督与强化学习探秘
  • 切入高潜市场，抢占行业先机！ES SHOW 2025展位预订火爆，10月28-30日共启增长新蓝海
  • flutter Function和自定义的Callback有什么区别?
  • 自动化三维测量仪工业零件自动外观三维测量-中科米堆CASAIM
  • Linux系统资源分配算法在VPS云服务器调优-性能优化全指南
  • 【DAB收音机】DAB 信号发生器介绍
  • C++源代码批量转码utf8
  • SystemVerilog学习【六】功能覆盖率详解
  • 【动态规划】简单多状态 dp 问题
  • 【lucene】advanceShallow (int target) 与advance(int target)
  • Kea DHCP高危漏洞CVE-2025-40779：单个数据包即可导致服务器崩溃
  • workflow/http_parser源码解密：HTTP解析器的双倍扩容与零拷贝策略
  • R 语言 eulerr 包绘制韦恩图：比例精准
  • 机器学习（讲解）
  • 使用MySQL计算斐波那契数列
  • 开源工具新玩法：cpolar提升Penpot协作流畅度
  • Spark入门：从零到能跑的实战教程
  • 基于Spring Session + Redis + JWT的单点登录实现
  • 在Ubuntu中安装配置MySql Server
  • [p2p-Magnet] docs | HTTP API与Web界面 | 搜索查询引擎
  • PyTorch 张量核心知识点
  • 引入资源即针对于不同的屏幕尺寸，调用不同的css文件
  • KubeBlocks For MySQL 云原生设计分享
  • 三大压测工具对比：Siege/ab/Wrk实战指南
  • SpringBoot系列之实现高效批量写入数据
  • 基础IO详解
  • 【前缀和】
  • Pandas的数据结构