牛客周赛 Round 104(小红的矩阵不动点/小红的不动点权值)
小红的矩阵不动点

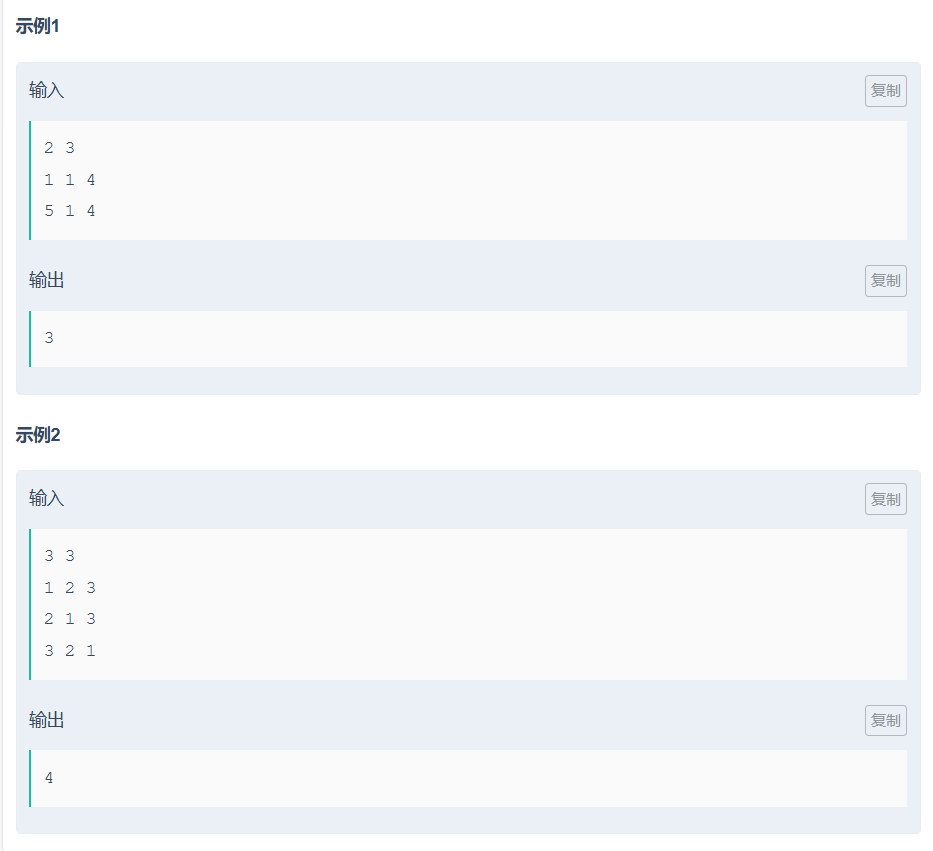
我们不难发现当i==j时,i或j任意一方增大都起不动点都是a[i][j]==z(z==i==j)。
因为数据最大为min(i,j)及500,所以我们可以用数组b[z][j]表示此位置min应为z,实际为j的个数
先计算不交换时 不动点个数 记为ans
则答案要么是ans+2 要么是ans+1 要么是ans
当且仅当两个数交换之后(b[z][j]>0&&b[j][z]>0时) 分别成为新的不动点时 答案为ans+2
当且仅当两个数交换之后 (i!=j&&b[i][j] > 0 && b[j][j] < (m + n-1 - 2 * (j - 1))只有一个成为新的不动点时 答案为ans+1,m + n-1 - 2 * (j - 1)表示该值最多有多少个不动点
否则 答案为ans.
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n, m;
int a[502][502], b[502][502];
int main() {ios::sync_with_stdio(false); // 禁用同步cin.tie(nullptr); // 解除cin与cout绑定cin >> n >> m;int ans = 0;int min_p = min(n, m);for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> a[i][j];}}for (int z = 1; z <= min_p; z++) {for (int j = z; j <= m; j++) {if (a[z][j] <= min_p) {b[z][a[z][j]]++;}}for (int i = z + 1; i <= n; i++) {if (a[i][z] <= min_p) {b[z][a[i][z]]++;}}}for (int i = 1; i <= min_p; i++) {int j;for ( j = 1; j <i; j++) {if (b[i][j] >0 && b[j][i] >0) {ans = 2;break;}}if (j <i) {break;}}if (ans == 0) {for (int i = 1; i <= min_p; i++) {int j;for (j = 1; j <= min_p; j++) {if (i!=j&&b[i][j] > 0 && b[j][j] < (m + n-1 - 2 * (j - 1))) {ans = 1;break;}}if (j < min_p) {break;}}}int sum = 0;for (int i = 1; i <= min_p; i++) {sum += b[i][i];}cout << sum+ans << endl;return 0;
}小红的不动点权值

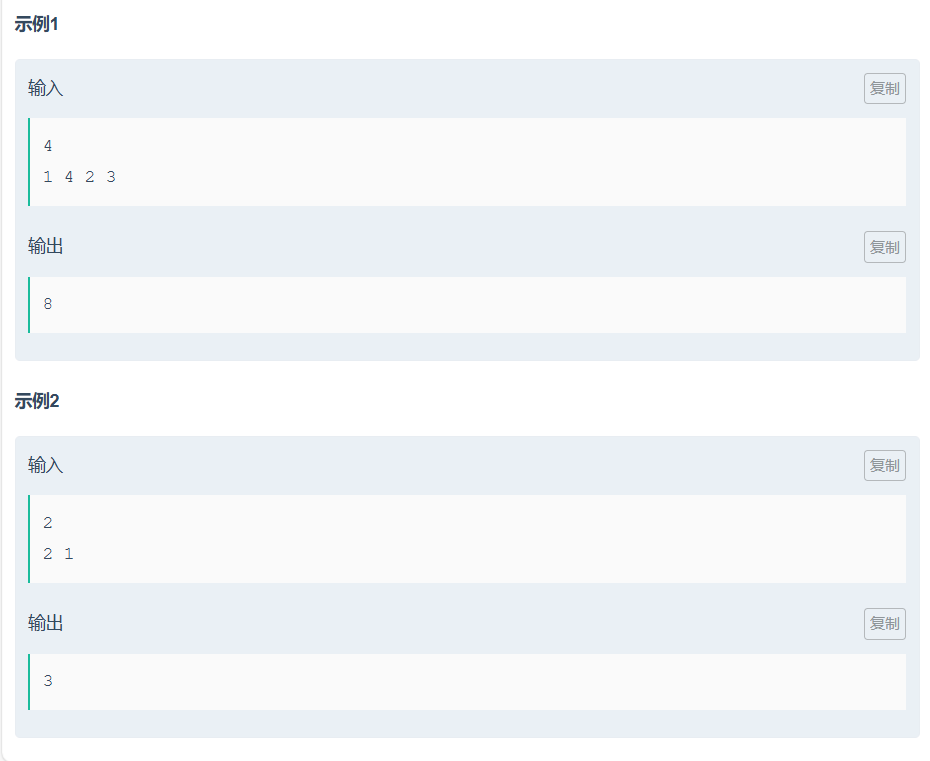
我们可以发现当i为不动点时,1-i-1个数都必须在区间内,所以我们根据这个找到最小区间的左右边界,i为不动点的区间就为 (long long)(n - r+1)* l
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int, int> pii;
int n;
pii a[300005];
int main() {ios::sync_with_stdio(false); // 禁用同步cin.tie(nullptr); // 解除cin与cout绑定cin >> n;for (int i = 0; i < n; i++) {cin >> a[i].first;a[i].second = i + 1;}int l, r;sort(a, a + n);ll ans = 0;for (int i = 0; i < n; i++) {if (i == 0) {l = a[i].second;r = a[i].second;}else {if (a[i].second < l) {l = a[i].second;}if (a[i].second > r) {r = a[i].second;}}ans += (ll)(n - r+1)* l;}cout << ans << endl;return 0;
}