Radar Forward-Looking Imaging Based on Chirp Beam Scanning论文阅读
Radar Forward-Looking Imaging Based on Chirp Beam Scanning
-
-
- 1. 论文研究目标与实际意义
-
- 1.1 核心问题
- 1.2 研究目标
- 1.3 产业意义
- 2. 基础模型与核心创新
-
- 2.1 传统前视成像的瓶颈
- 2.2 调频波束扫描(CBS)的核心框架
-
- 2.2.1 调频波束定义与物理意义
- 2.2.2 调频波束的硬件实现:均匀线阵(ULA)激励设计
- 2.2.3 CBS成像流程与二维脉冲压缩
- 2.2.4 超分辨策略:稀疏表示(SR)与调频字典
- 2.3 与传统方法性能对比
- 关键创新总结
- 3. 实验验证与结果
-
- 3.1 仿真实验
- 3.2 实测验证
- 4. 未来研究方向
-
- 4.1 技术挑战
- 4.2 创新机遇
- 5. 批判性评价
-
- 5.1 局限性
- 5.2 未验证问题
- 6. 可复用创新与学习建议
-
- 6.1 核心可迁移技术
- 6.2 必备背景知识补充
-
1. 论文研究目标与实际意义
1.1 核心问题
雷达前视成像(Radar Forward-Looking Imaging)在飞行器导航、自动驾驶等场景中至关重要,但其方位分辨率受限于物理孔径尺寸 D D D,理论极限为 λ / D \lambda/D λ/D。传统合成孔径雷达(SAR)无法对正前方目标生成等效大孔径,导致前视场景成像质量低下。
1.2 研究目标
提出一种基于调频波束扫描(Chirp Beam Scanning, CBS) 的新型成像方法,通过主动调制天线波束模式,在方位维度生成类调频信号的“宽频带”特性,结合脉冲压缩技术与稀疏表示(Sparse Representation, SR),突破物理孔径的方位分辨率限制。
1.3 产业意义
- 自动驾驶:提升前向障碍物分辨能力(如相邻车辆分离)
- 航空导航:增强低能见度条件下跑道异物检测精度
- 军事应用:解决导弹末端制导的高精度前视成像需求
2. 基础模型与核心创新
2.1 传统前视成像的瓶颈
物理限制:方位分辨率理论极限为 λ / D \lambda/D λ/D( D D D为孔径, λ \lambda λ为波长),传统实波束扫描(Real Beam Imaging, RBI)无法突破此限制。
模型对比:
距离维:回波 s ( t ) = 发射波形 ∗ 目标分布 s(t) = \text{发射波形} * \text{目标分布} s(t)=发射波形∗目标分布 → 脉冲压缩可解耦
方位维:回波 s ( ϕ ) = 天线方向图 ∗ 目标角分布 s(\phi) = \text{天线方向图} * \text{目标角分布} s(ϕ)=天线方向图∗目标角分布 → 方向图未调制,分辨率受限
传统方法仅在距离维通过脉冲压缩(Pulse Compression) 实现高分辨率(因发射信号已调制为宽带),而方位维被视为“窄带脉冲”,分辨率被硬件限制。
2.2 调频波束扫描(CBS)的核心框架
2.2.1 调频波束定义与物理意义
创新思想:将方位维回波重构为「脉冲压缩问题」,需主动调制波束方向图使其具备「宽频带」特性。 通过阵列激励调制,在主瓣内引入二次相位变化,定义调频波束(Chirp Beam):
数学定义(式1):
E chirp ( φ , ϕ ) = rect ( φ − ϕ Φ 0 ) exp ( j 2 π K a 2 ( φ − ϕ ) 2 ) E_{\text{chirp}}(\varphi,\phi)=\text{rect}\left(\frac{\varphi-\phi}{\Phi_{0}}\right)\exp\left(j2\pi\frac{K_{a}}{2}(\varphi-\phi)^{2}\right) Echirp(φ,ϕ)=rect(Φ0φ−ϕ)exp(j2π2Ka(φ−ϕ)2)
- φ \varphi φ:目标方位角
- ϕ \phi ϕ:波束指向角(扫描变量)
- Φ 0 \Phi_0 Φ0:波束主瓣宽度
- K a K_a Ka:方位调频率(单位 rad − 2 \text{rad}^{-2} rad−2),控制相位二次变化率
物理意义:在波束主瓣内引入线性调频(Chirp)相位,使方位回波具备频率啁啾特性,为脉冲压缩奠定基础。
2.2.2 调频波束的硬件实现:均匀线阵(ULA)激励设计
基于均匀线阵(Uniform Linear Array, ULA) 的MISO雷达架构(图1):
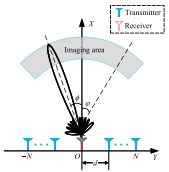
关键方程:阵列方向图 = 期望调频波束(式3)
E chirp ( φ , ϕ ) = ∑ n = − N N I n ( ϕ ) ⋅ exp ( j 2 π f c n d sin φ c ) E_{\text{chirp}}(\varphi,\phi)=\sum_{n=-N}^{N}I_{n}(\phi)\cdot\exp\left(j2\pi f_{c}\frac{nd\,\sin\varphi}{c}\right) Echirp(φ,ϕ)=n=−N∑NIn(ϕ)⋅exp(j2πfc
