当前位置：首页 > java >正文

机器学习——07 朴素贝叶斯

java 2025/8/14 1:28:54

1 概述

朴素贝叶斯算法是一种基于贝叶斯定理的分类算法，它利用概率值来进行分类。其核心思想是根据已有的数据样本，计算在不同条件下某一事件发生的概率，从而实现对新样本的分类预测。

1.1 概率相关数学知识

什么是概率？
- 概率是对一件事情发生可能性的度量，取值范围在 $[0, 1]$ 之间；
- 概率值越接近1，表示事件发生的可能性越大；越接近0，表示事件发生的可能性越小；
- 例如抛硬币正面向上的概率是 $0.5$ ，6面骰子抛出5这一面的概率是 $16\frac{1}{6}$ ；
条件概率表示在事件 $B$ 已经发生的条件下，事件 $A$ 发生的概率，记为 $P (A ∣ B)$ ；
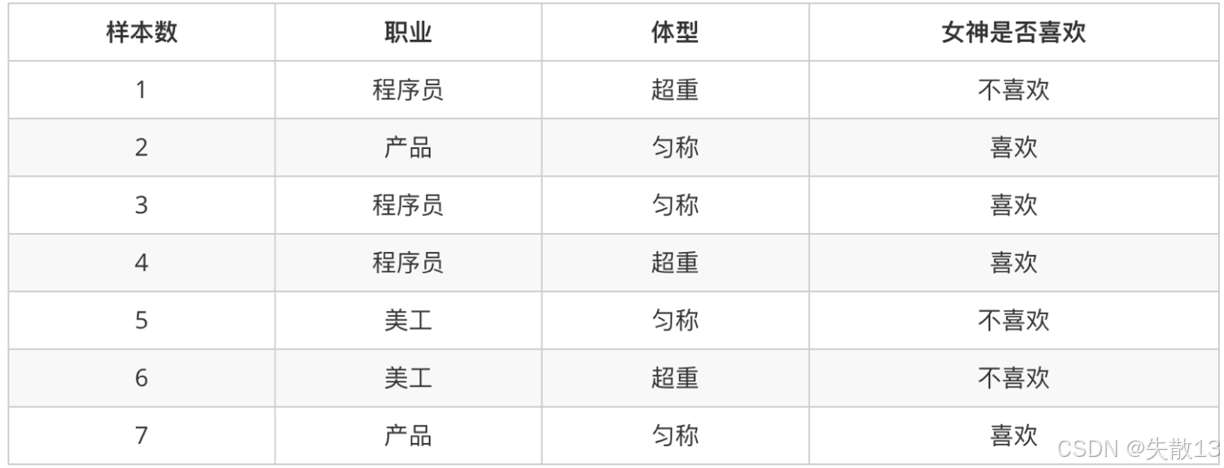
- 示例：在女神喜欢的条件下，职业是程序员的概率
  - 首先确定女神喜欢的样本有样本2、3、4、7，共4个
  - 然后在这4个样本中，职业是程序员的有样本3、4，共2个
  - 所以 $P(程序员∣喜欢)=24=0.5P(\text{程序员}|\text{喜欢}) = \frac{2}{4} = 0.5$
- 思考问题：在女神不喜欢的条件下，职业是程序员的概率是多少？
  - 首先找出女神不喜欢的样本，即样本1、5、6，共3个
  - 然后在这3个样本中，职业是程序员的只有样本1，共1个
  - 因此 $P(程序员∣不喜欢)=13P(\text{程序员}|\text{不喜欢}) = \frac{1}{3}$
联合概率表示多个条件同时成立的概率，记为 $P (A B)$ 。条件概率公式： $\times P(B|A) = P(B) \times P(A|B)$
- 示例：职业是程序员并且体型匀称的概率
  - 数据集中共有7个样本
  - 职业是程序员的样本有1、3、4，共3个，所以 $P(程序员)=37P(\text{程序员}) = \frac{3}{7}$
  - 在职业是程序员的样本中，体型匀称的有样本3，共1个，所以 $P(匀称∣程序员)=13P(\text{匀称}|\text{程序员}) = \frac{1}{3}$
  - 则 $P(程序员且匀称)=P(程序员)×P(匀称∣程序员)=37×13=17P(\text{程序员且匀称}) = P(\text{程序员}) \times P(\text{匀称}|\text{程序员}) = \frac{3}{7} \times \frac{1}{3} = \frac{1}{7}$
- 思考问题：体型匀称并且是程序员的概率是多少？
  - 首先计算 $P(匀称)P(\text{匀称})$ ，体型匀称的样本有2、3、5、7，共4个，所以 $P(匀称)=47P(\text{匀称}) = \frac{4}{7}$
  - 然后计算 $P(程序员∣匀称)P(\text{程序员}|\text{匀称})$ ，在体型匀称的样本中，职业是程序员的有样本3，共1个，所以 $P(程序员∣匀称)=14P(\text{程序员}|\text{匀称}) = \frac{1}{4}$
  - 因此 $P(匀称且程序员)=P(匀称)×P(程序员∣匀称)=47×14=17P(\text{匀称且程序员}) = P(\text{匀称}) \times P(\text{程序员}|\text{匀称}) = \frac{4}{7} \times \frac{1}{4} = \frac{1}{7}$
联合概率与条件概率的结合。例如：在女神喜欢的条件下，职业是程序员并且超重的概率，即 $P(程序员，超重∣喜欢)P(\text{程序员，超重}|\text{喜欢})$
- 首先确定女神喜欢的样本有4个（样本2、3、4、7）
- 在这4个样本中，职业是程序员的有样本3、4，共2个，所以 $P(程序员∣喜欢)=24=0.5P(\text{程序员}|\text{喜欢}) = \frac{2}{4} = 0.5$
- 在职业是程序员且女神喜欢的样本中，体型超重的有样本4，共1个，所以 $P(超重∣程序员且喜欢)=12=0.5P(\text{超重}|\text{程序员且喜欢}) = \frac{1}{2} = 0.5$
- 则 $P(程序员，超重∣喜欢)=0.5×0.5=0.25P(\text{程序员，超重}|\text{喜欢}) = 0.5 \times 0.5 = 0.25$
相互独立：
- 如果 $P (A, B) = P (A) P (B)$ ，则称事件 $A$ 与事件 $B$ 相互独立；
- 这意味着事件 $A$ 的发生与否不影响事件 $B$ 发生的概率，反之亦然；
- 例如女神喜欢程序员的概率和女神喜欢产品经理的概率是相互独立的，这两个事件之间没有关系。
总结
- 条件概率：在去掉部分样本的情况下，计算某些样本出现的概率，表示为 $P (B ∣ A)$
- 联合概率：多个事件同时发生的概率，表示为 $\times P(A|B)$

1.2 贝叶斯公式

贝叶斯公式是朴素贝叶斯算法的核心公式，表达式为：
$\frac{P(W|C)P(C)}{P(W)}$
- 其中：
  - $P (C)$ ：表示类别 $C$ 出现的概率，通常是我们要预测的目标类别（比如“喜欢”）的先验概率
  - $P (W ∣ C)$ ：表示在类别 $C$ 发生的条件下，特征 $W$ （比如“程序员”和“超重”这两个特征的组合）出现的条件概率
  - $P (W)$ ：表示特征 $W$ 出现的概率
例：以表格中的编号1为例，计算“职业是程序员且体型超重”的情况下“女神喜欢”的概率，即 $P(喜欢∣程序员，超重)P(\text{喜欢}|\text{程序员，超重})$ 。根据贝叶斯公式，可以将其分解为：
- $P(\text{喜欢}|\text{程序员，超重})$
- $P(\text{程序员，超重}|\text{喜欢})$
- $P(\text{喜欢})$
- $P(\text{程序员，超重})$
接下来应用贝叶斯公式来计算后验概率：
1. 计算先验概率 $P (C)$ ：
  - $P(喜欢)P(\text{喜欢})$ 表示在所有样本中“女神喜欢”的概率
  - 从之前的样本数据可知，总共有7个样本，其中“喜欢”的样本有4个，所以 $P(喜欢)=47P(\text{喜欢}) = \frac{4}{7}$
2. 计算条件概率 $P (W ∣ C)$ ：
  - $P(程序员，超重∣喜欢)P(\text{程序员，超重}|\text{喜欢})$ 表示在“女神喜欢”的条件下，“职业是程序员且体型超重”的概率
  - 在“喜欢”的4个样本中，“职业是程序员且体型超重”的样本有1个，所以 $P(程序员，超重∣喜欢)=14P(\text{程序员，超重}|\text{喜欢}) = \frac{1}{4}$
3. 计算后验概率 $P (C ∣ W)$ ：根据贝叶斯公式， $P(喜欢∣程序员，超重)=P(程序员，超重∣喜欢)×P(喜欢)=14×47=17P(\text{喜欢}|\text{程序员，超重}) = P(\text{程序员，超重}|\text{喜欢}) \times P(\text{喜欢}) = \frac{1}{4} \times \frac{4}{7} = \frac{1}{7}$
4. 计算特征 $W$ 的概率 $P (W)$ ：
  - $P(程序员，超重)P(\text{程序员，超重})$ 表示“职业是程序员且体型超重”的概率
  - 计算 $P(程序员)=37P(\text{程序员}) = \frac{3}{7}$ （总共有3个程序员样本）， $P(超重∣程序员)=23P(\text{超重}|\text{程序员}) = \frac{2}{3}$ （在3个程序员样本中，有2个体型超重）
  - 所以 $P(程序员，超重)=P(程序员)×P(超重∣程序员)=37×23=27P(\text{程序员，超重}) = P(\text{程序员}) \times P(\text{超重}|\text{程序员}) = \frac{3}{7} \times \frac{2}{3} = \frac{2}{7}$
5. 最终计算后验概率： $P(喜欢∣程序员，超重)=17÷27=0.5P(\text{喜欢}|\text{程序员，超重}) = \frac{1}{7} \div \frac{2}{7} = 0.5$

1.3 朴素贝叶斯

朴素贝叶斯算法在贝叶斯公式的基础上增加了一个关键的假设：特征条件独立假设。即假设各个特征之间是相互独立的，一个特征的出现不会影响另一个特征的出现概率；
此时，基于特征条件独立假设，联合概率的计算可以简化为：
- $P(程序员，超重∣喜欢)=P(程序员∣喜欢)×P(超重∣喜欢)P(\text{程序员，超重}|\text{喜欢}) = P(\text{程序员}|\text{喜欢}) \times P(\text{超重}|\text{喜欢})$
  - 这是因为在“喜欢”的条件下，“程序员”和“超重”这两个特征是相互独立的，所以它们的联合概率等于各自条件概率的乘积；
- $P(程序员，超重)=P(程序员)×P(超重)P(\text{程序员，超重}) = P(\text{程序员}) \times P(\text{超重})$
  - 同样，在不考虑任何条件的情况下，“程序员”和“超重”这两个特征也是相互独立的，所以它们的联合概率等于各自概率的乘积；
通过这种简化，朴素贝叶斯算法大大降低了计算的复杂度，使得它在处理高维数据时仍然具有较高的效率。

1.4 拉普拉斯平滑系数

在朴素贝叶斯算法中，当计算条件概率时，如果某个特征在训练数据中没有出现过，那么它的概率就会被计算为0。这会导致后续的概率计算出现问题，因为0乘以任何数都为0。为了避免这种情况，我们引入了拉普拉斯平滑系数。它的作用是在分子和分母上分别加上一个数值，从而避免概率值为0的情况；
拉普拉斯平滑系数的公式为：
$P(F_1|C) = \frac{N_i + \alpha}{N + \alpha m}$
- 其中：
  - $α\alpha$ ：是拉普拉斯平滑系数，一般指定为1。
  - $N_i$ ：是特征 $F_1$ 中符合条件 $C$ 的样本数量。
  - $N$ ：是在条件 $C$ 下所有样本的总数。
  - $m$ ：表示所有独立样本的总数。
例：假设我们有一个分类问题，要计算特征 $F_1$ 在类别 $C$ 下的条件概率
- 如果在训练数据中，特征 $F_1$ 在类别 $C$ 下没有出现过，那么 $N_i = 0$ 。如果没有拉普拉斯平滑， $P(F1∣C)=0N=0P(F_1|C) = \frac{0}{N} = 0$ 。这会导致在后续的分类中，这个特征的概率为0，从而影响分类结果；
- 通过引入拉普拉斯平滑系数 $α=1\alpha = 1$ ，公式变为：
  $P(F_1|C) = \frac{0 + 1}{N + 1 \times m}$
- 这样，即使 $N_i = 0$ ， $P(F_1|C)$ 也不会为0，从而避免了概率值为0的问题。

2 案例：商品评论情感分类

2.1 API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- MultinomialNB：这是sklearn库中实现多项式朴素贝叶斯分类器的类。多项式朴素贝叶斯常用于文本分类问题，尤其是在特征是离散值的情况下（例如词频）；
- alpha：这是拉普拉斯平滑系数，用于避免概率值为 0 的情况。默认值为 1.0；

2.2 案例：商品评论情感分类

需求：已知商品评论数据，根据数据进行情感分类（好评、差评）；

导包：

import pandas as pd
import numpy as np
import jieba # 用于中文分词
from sklearn.feature_extraction.text import CountVectorizer # 文本特征提取
from sklearn.naive_bayes import MultinomialNB # 朴素贝叶斯分类器

读取数据：

# 读取数据
data =pd.read_csv('data/书籍评价.csv', encoding='gbk')
print(data)# 将评价标签转换为数值型：好评记为1，其他（差评）记为0
data['labels']=np.where(data['评价']=='好评',1,0)
print(data)
y = data['labels']

加载停用词表
- 停用词（stop words）的作用主要是为了过滤掉文本中一些常见的、没有实际意义的词汇，这些词汇通常对文本的主题或情感分析没有太大的帮助。具体来说，停用词的作用包括以下几个方面：
  - 减少噪声：文本中可能包含大量的虚词、介词、连词等，这些词汇在文本中出现的频率很高，但对于理解文本的主题或情感并没有太大的作用。例如，“的”、“了”、“在”等词汇。通过过滤这些停用词，可以减少文本中的噪声，使模型更加关注那些对分类有重要意义的词汇；
  - 降低维度：如果不使用停用词，文本中的词汇量可能会非常大，这会导致特征空间的维度很高。高维度的特征空间不仅会增加计算的复杂度，还可能会导致过拟合等问题。通过过滤停用词，可以减少特征的数量，降低特征空间的维度，从而提高模型的效率和泛化能力；
  - 提高模型性能：使用停用词可以使模型更加关注那些对分类有重要意义的词汇，从而提高模型的性能。例如，在情感分析任务中，一些情感词汇（如“好”、“坏”、“满意”等）对分类结果的影响很大，而一些停用词（如“的”、“了”等）对分类结果的影响很小。通过过滤停用词，可以使模型更加关注这些情感词汇，从而提高模型的准确率；
```
# 加载停用词表
stop_words = []
# # 读取停用词文件，这些词通常是无实际意义的虚词、助词等
with open('data/stopwords.txt', encoding='utf-8') as file:lines=file.readlines()# 去除每行的换行符并添加到停用词列表stop_words = [line.strip() for line in lines]
# 去重，确保每个停用词只出现一次
stop_words = list(set(stop_words))
print(stop_words)
```

文本分词与特征提取：

# 文本分词与特征提取
# 对每条评价内容进行分词处理，并用逗号连接成字符串
# jieba.lcut(line)将文本分割成词语列表
word_list=[','.join(jieba.lcut(line)) for line in data['内容']]
print(word_list)

在这里插入图片描述

词频统计
- 词频统计（通过CountVectorizer实现）是将文本数据转换为机器学习模型可处理的数值特征的核心步骤，其主要作用如下：
  - 将文本转化为数值特征。机器学习模型（包括朴素贝叶斯）只能处理数值型数据，而原始文本是字符串形式（如“这本书内容丰富，非常推荐”）。词频统计通过计算每个词语在文本中出现的次数，将文本转换为“词频矩阵”（每行代表一篇文本，每列代表一个词语，单元格值为该词语在对应文本中的出现次数）。例如，若词汇表为["内容", "丰富", "推荐"]，则文本“内容丰富，内容推荐”会被转换为[2, 1, 1]（“内容”出现2次，“丰富”出现1次，“推荐”出现1次）；
  - 提取文本关键信息。词频统计能间接反映词语对文本类别的“重要性”。在情感分析任务中，情感倾向强烈的词（如“好”“差”“推荐”“失望”）通常在某一类文本中出现频率更高。模型通过学习这些词的频率分布，可推断文本的类别（如“好评”或“差评”）；
  - 为朴素贝叶斯提供概率计算依据。朴素贝叶斯算法的核心是基于“词频”计算条件概率。例如，通过统计“好评”文本中“推荐”一词的出现次数，可计算P(推荐|好评)（在好评中“推荐”出现的概率），进而结合贝叶斯公式判断新文本的情感倾向。词频统计直接为这些概率计算提供了基础数据；
  - 简化文本特征。词频统计会过滤掉停用词（如“的”“在”等无意义词汇），并只保留有实际意义的词语作为特征，既减少了特征维度（降低计算量），又避免了无意义词汇对模型的干扰；
```
# 词频统计
# 初始化CountVectorizer，用于将文本转换为词频矩阵。设置停用词表，这些词将不被计入词频统计
transform =CountVectorizer(stop_words=stop_words)
# 将分词后的文本列表转换为词频矩阵
x =transform.fit_transform(word_list)
# 获取所有特征词（词汇表）
names = transform.get_feature_names_out()
print(names)  # 打印词汇表
print(len(names))  # 打印词汇表大小
x = x.toarray()  # 将稀疏矩阵转换为稠密矩阵
print(x)  # 打印词频矩阵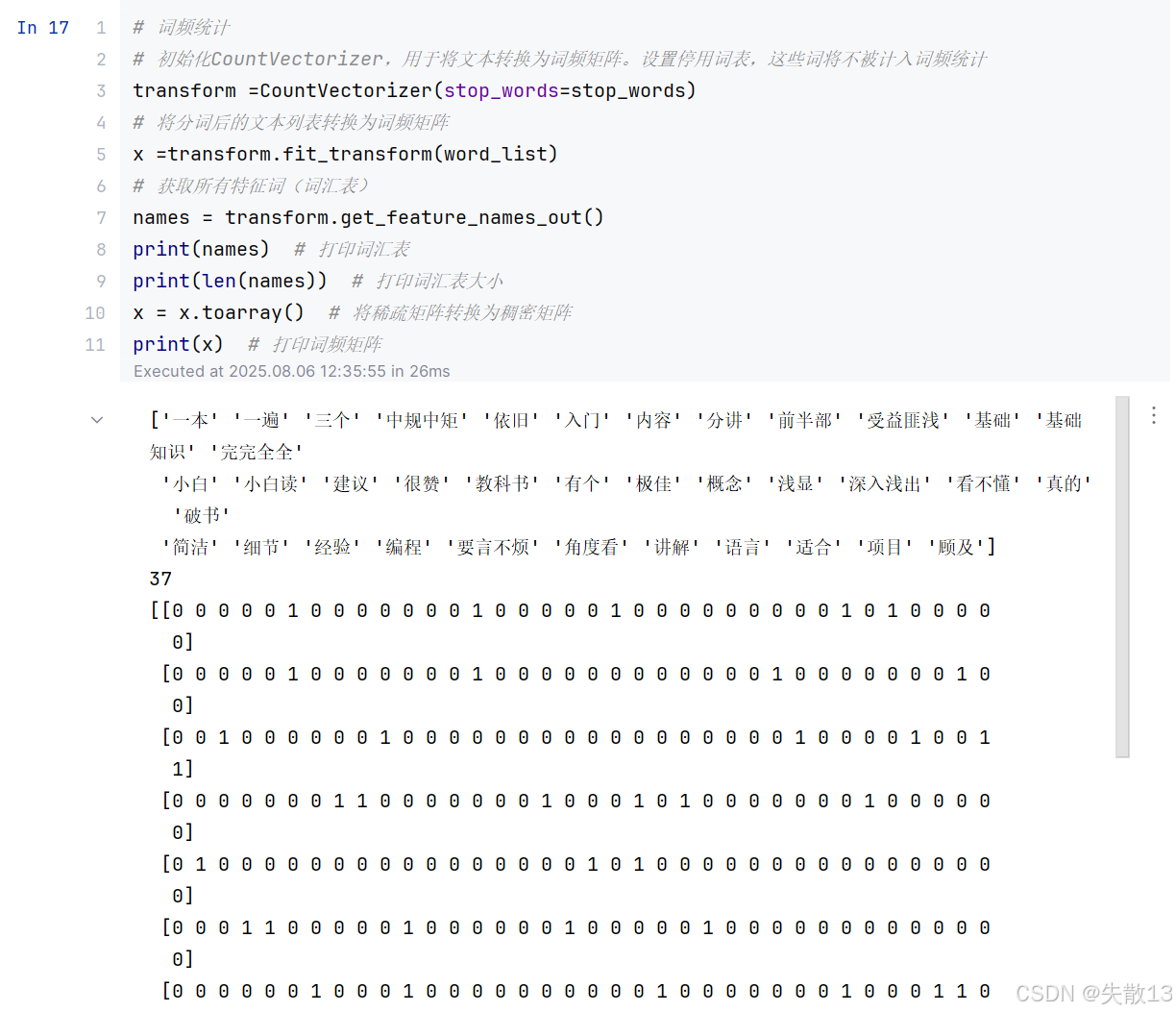
```

划分训练集与测试集

# 划分训练集和测试集
x_train=x[:10,:]
y_train=y.values[0:10]
x_test=x[10:,:]
y_test=y.values[10:]

模型训练与评估
```
# 模型训练与评估
# 初始化多项式朴素贝叶斯分类器，设置拉普拉斯平滑系数alpha=1
model =MultinomialNB(alpha=1)
model.fit(x_train,y_train)y_predict=model.predict(x_test)
print(y_predict)
print(model.score(x_test,y_test))
```
- [0 0 0]：这是模型对测试集的预测结果，表示模型预测这三个测试样本的类别均为 0。
- 1.0：这是模型在测试集上的准确率，说明模型对这三个测试样本的预测全部正确，准确率为 100%。