01数据结构-并查集

前言

树的基本查找我们已经讲完了，后面高阶搜索树我们后面再说，先来看树的两个应用，一个是并查集，一个是哈夫曼树，今天呢我们先讲并查集。

1.并查集

1.1需求分析

假设现在有这样一个需求，如下图1的每一个点代表一个村庄，每一条线代表一条路，所以有些村庄之间有连接的路有些村庄没有连接的路，但是有间接连接的路，根据上面的条件，能设计出一个数据结构，能快速执行下面两个操作：

• 1.查询两个村庄之间是否有连接的路
• 2.连接两个村庄

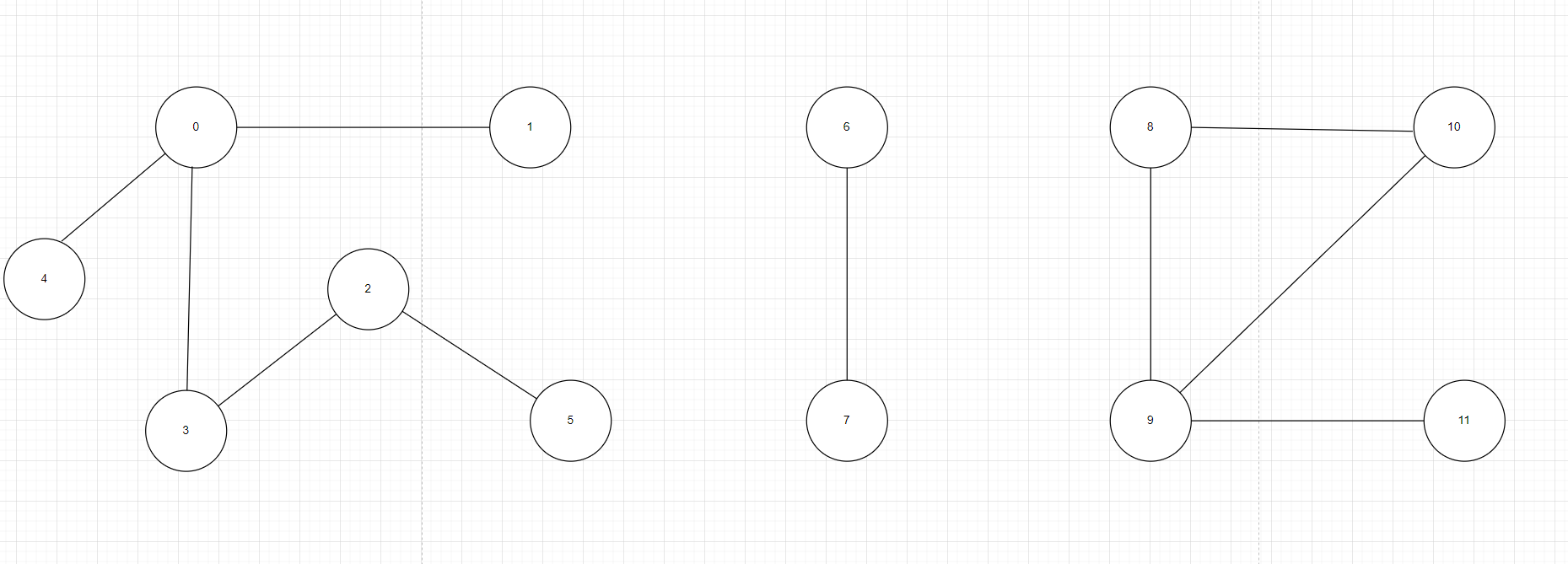
图1

按照图1可以发现，1可以和0，2，3，4，5号村庄通信但没办法和6，7号，8，9，10，11号村庄通信，图1很明显分三种不同的集合，在有些场合中我们想判断两个数在不在一个集体当中或者我们想组合第一二个集合，使村庄变得更加强大，所以就提出了能不能快速判断两个元素是否属于同一集合和合并两个元素这种需求，我们就提出了并查集。虽然图1中看上去很简单，一眼就知道两个元素是否能通信，但是实际情况会比这复杂很多，看下图2，要想知道两个黑点是否在一个集合中，就不能看出来了，要用到我们今天讲的并查集。

图2

1.2并查集的定义

并查集是一种非常精巧而实用的树形数据结构，他主要是处理一些不相交集合的合并和查询的问题。不相交集合，顾名思义，就是两个集合的交集为空集的一些集合。比如1，3，5和2，4，6，他俩的交集为空集。就是不相交集合。像2，3，5和1，3，5就不是不相交集合。

使用并查集时，首先会存在一组不相交的动态集合 S={S1, S2,⋯,Sk}，一般都会使用一个整数表示集合中的一个元素。

每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级。

并查集支持以下操作：

• 查询(Find)：查询某个元素属于哪个集合，通常是返回集合内的“代表元素”。这个操作是为了判断两个元素是否在同一集合
• 合并(Union)：将两个集合合并为一个
• 添加：添加一个新集合，其中有一个新元素，添加操作不如查询和合并操作重要，常常被忽略。

如果图3先不要看右边，右边是左边操作执行完的结果，一步一步地看左边的操作，在第一次find（0，2）和find（0，4）之前的如图4，所以此时find（0，2）是no，find（2，4）是yes，在执行完所有union后如图3右边，此时find（0，2）是yes，find（2，4）也是yes。下面来看并查集的算法逻辑

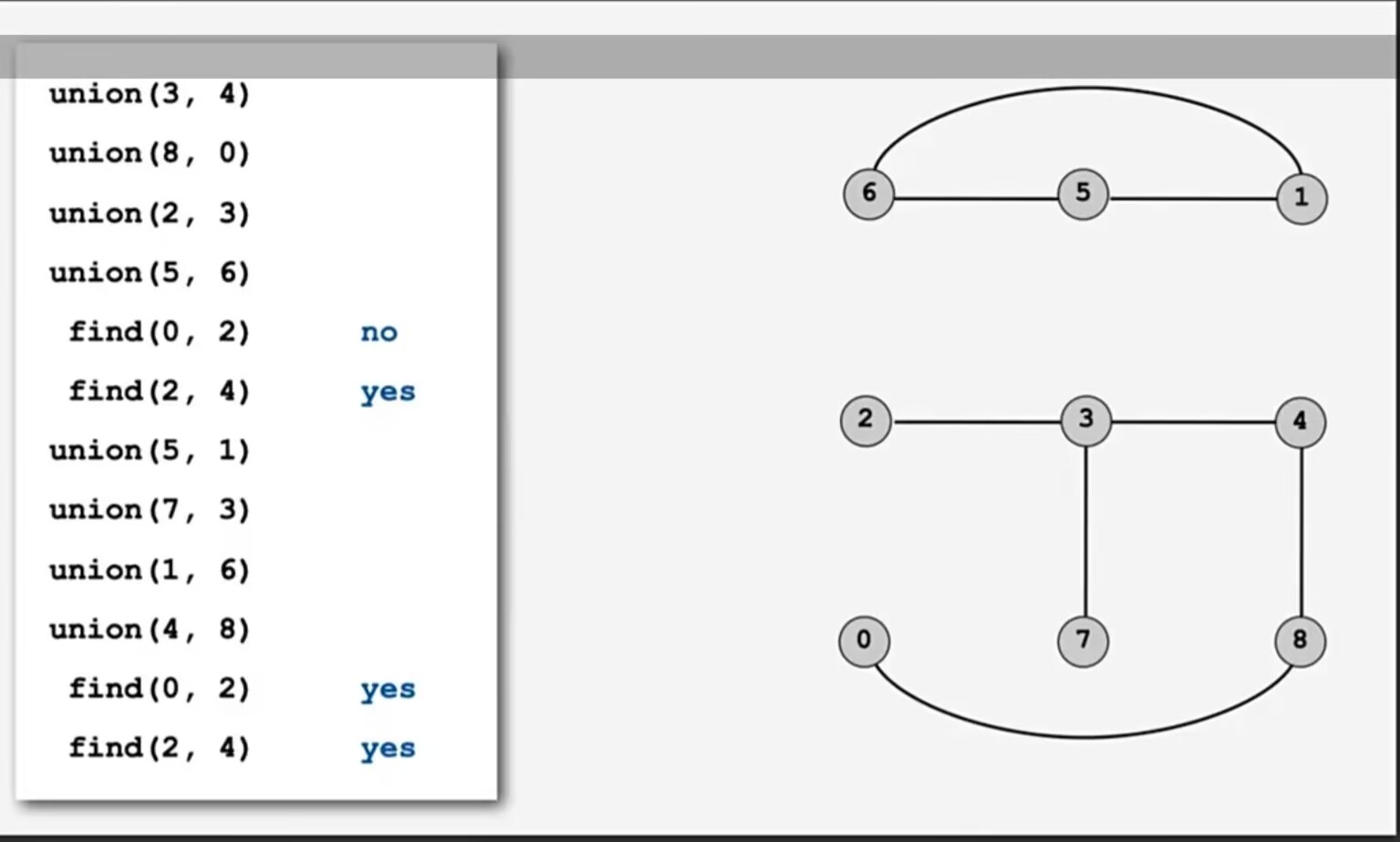
图3

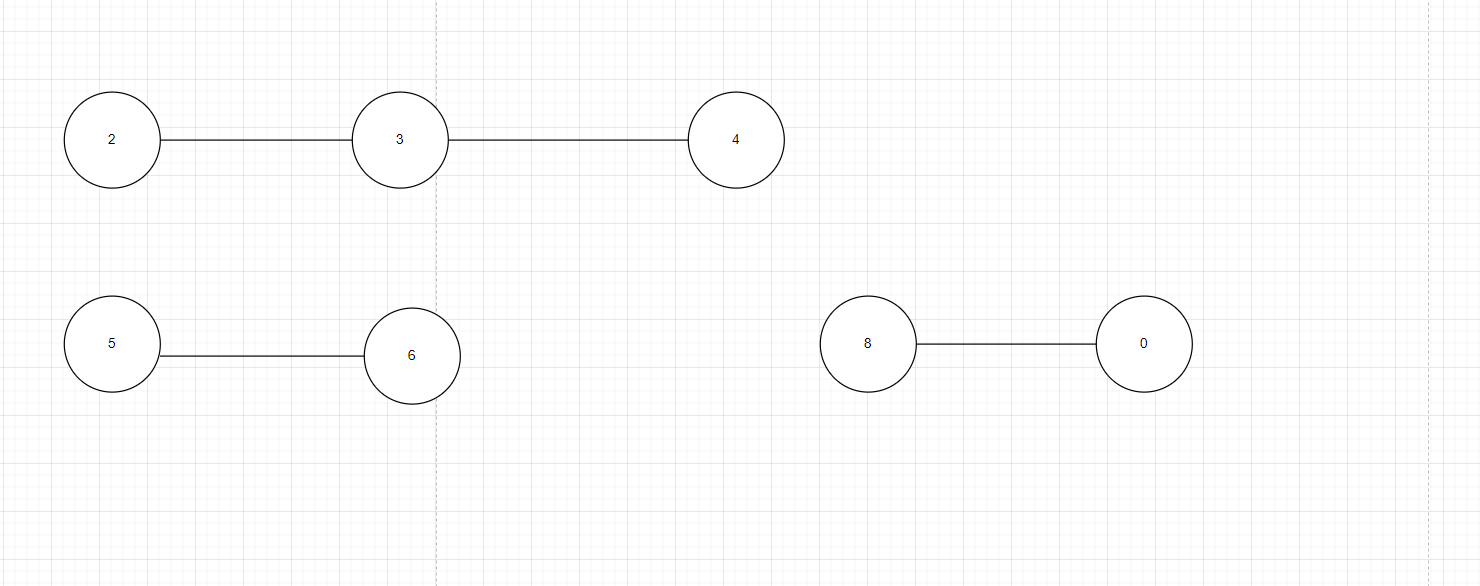
图 4

2.并查集的算法介绍

• 并查集有两种常见的实现思路
  • a.Quick find
    • 查找效率O(1)
    • 合并效率O(N)
  • b.Quick Union
    • 查找效率：O(logN)
    • 合并效率：O(logN)

2.1Quick find的思路

• 核心是将所有元素进行分组管理，每个元素对应一个组ID号(引入一个辅助空间存组ID号)
• find的时候，只需要返回这个元素对应的组ID号
• 合并的时候Union(a,b)的时候，将是属于a分组的元素，都改为b分组的ID号

如图5，我们可以实现一个数组存放具体数据，但实际的数据域不会只是A,B,C…这么简单，所以我们想要维护实际的数据域就会很困难，如图我们给每个数据域中的数据建立一个索引，利用索引来建立数据元素的关系。我们用索引来代表数据，初始时没有Union，我们就认为每个数据都是单独的，自己就是自己的老大

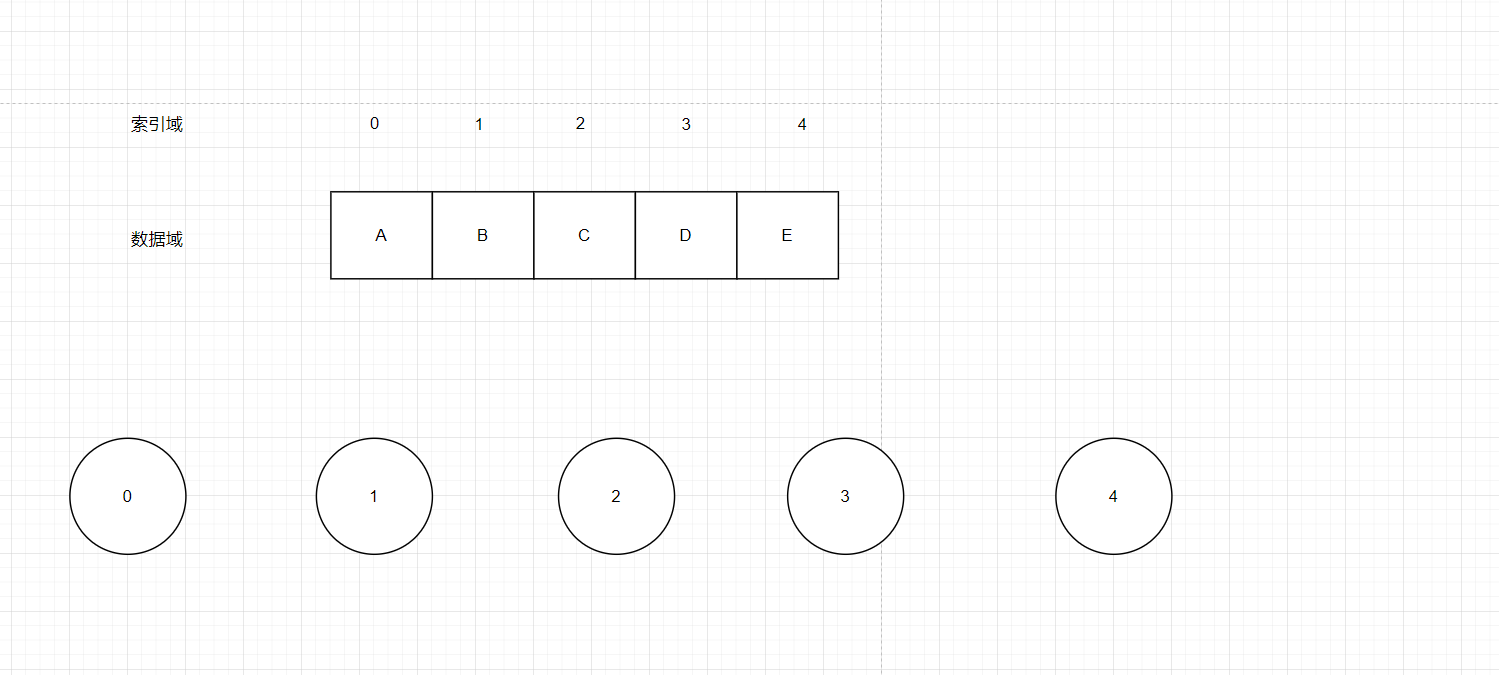
图5

如图6在数据域上我们建立一个关系域(辅助空间)，我们Union和find就在关系域中查找，并把这个关系域取名为group_id,我们Union(0,3)，就把关系域中所有0的数据改为3或者关系域中所有3的数据改为0，都可以，看自己代码咋写,find的时候看两个0和3两个数据在关系域中是否是同一个老大

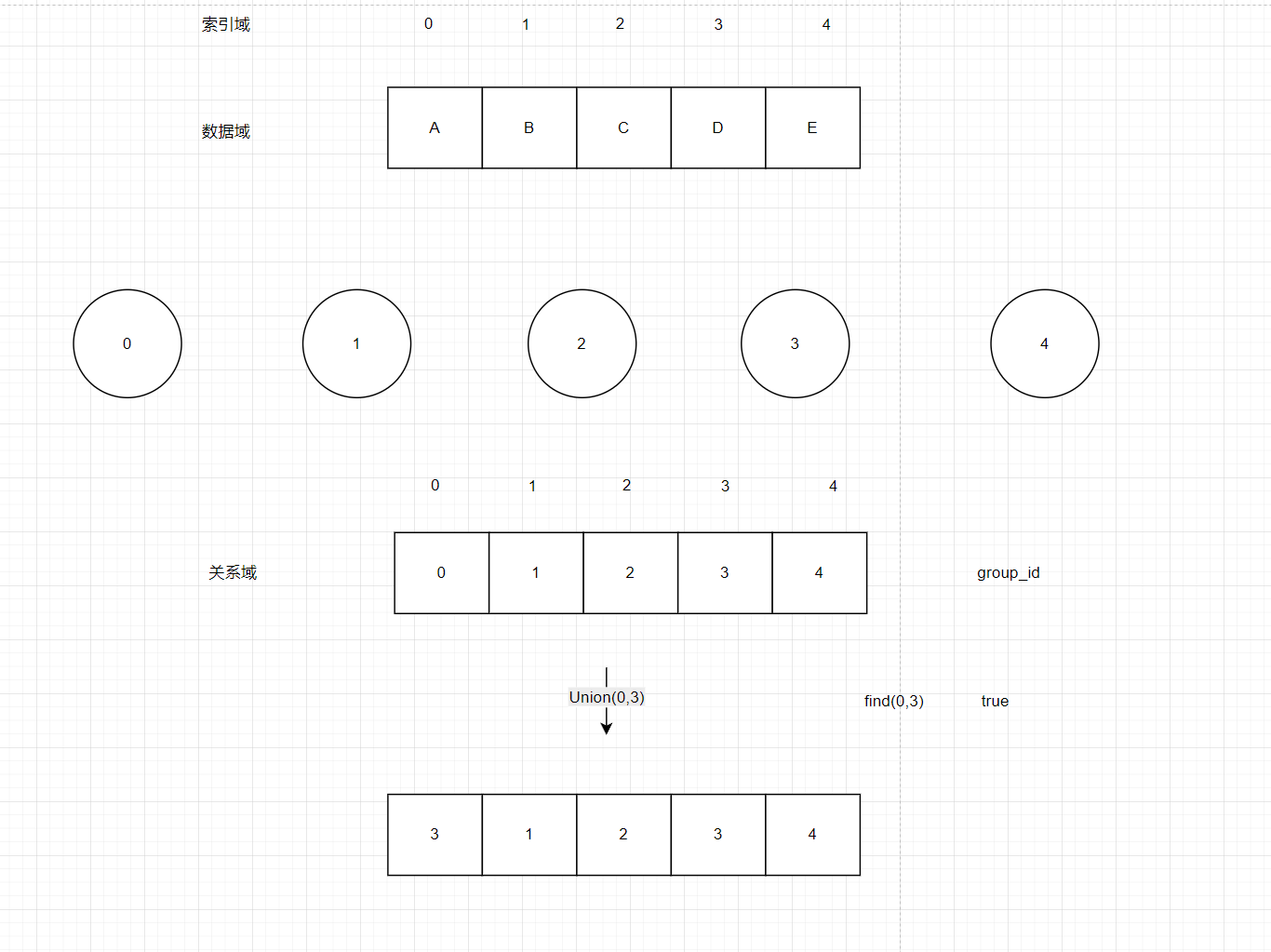
图6

如图7就是Union的过程，在执行第三步Union(0,4)，就查找关系域中的所有0号索引的相同数据将他们全部改为索引为4的关系域中的数据

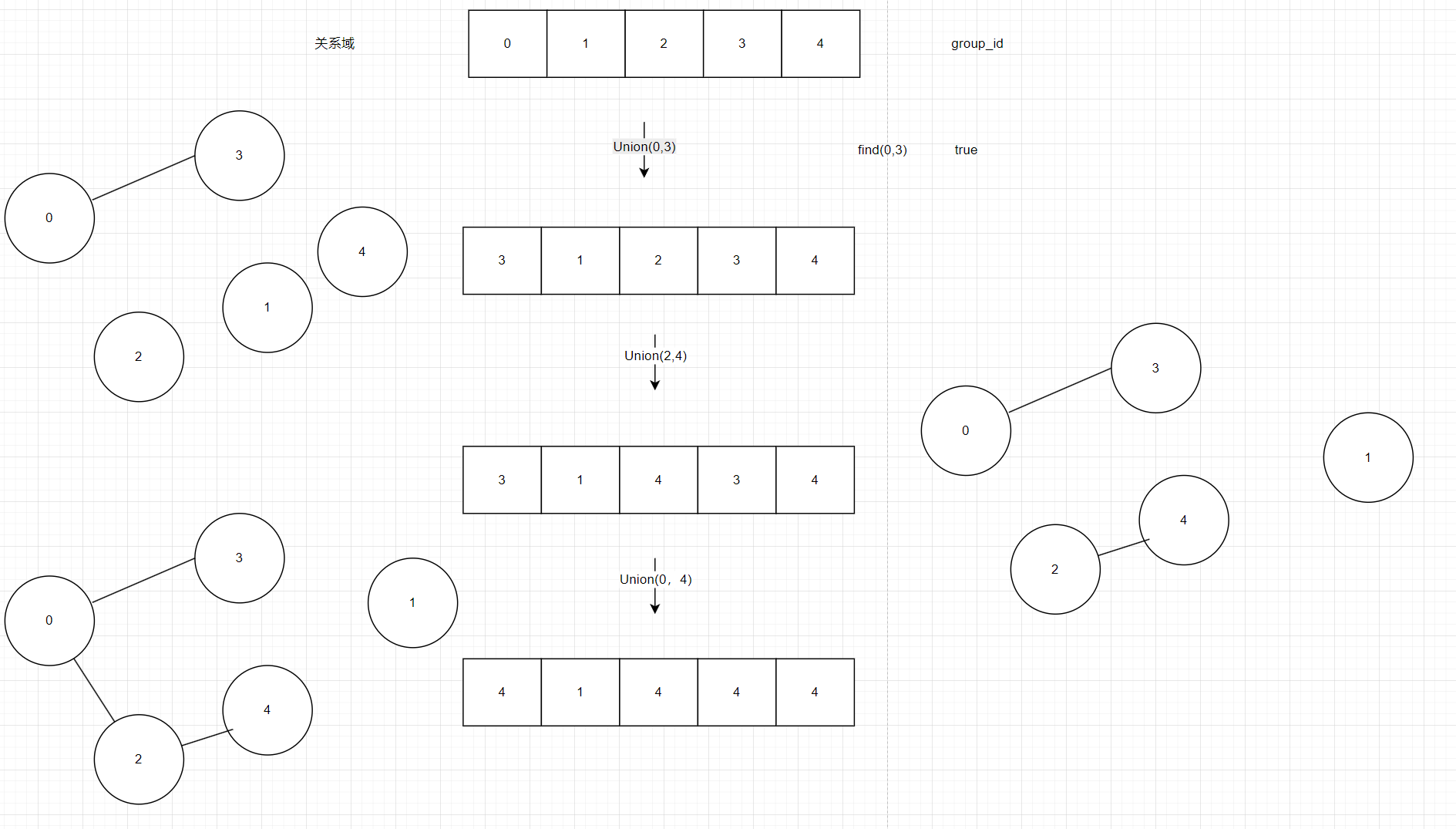
图7

2.1.1Union(x,y)和Find(x,y)的伪代码

• Union(x,y):查找x的组ID w，查找y的组ID u,判断是否相等把所有组ID是w的组ID，更新为u。时间复杂度：O(N)（有几个w就需要遍历几遍，把所有w换成u）
• Find(x,y)::查找x的组ID w，查找y的组ID u,判断是否相等，如果相等，返回ture。时间复杂度：O©（直接下标查找）

2.2Quick Union的思路

• 将集合分为根节点和父节点的思想，所有节点保存他的父节点信息，当发现某个节点的父节点就是他自己时，这个节点就是根节点
• find操作就是找到这个元素的根节点，判断两个元素的根节点是不是一致，来判断是否连通
• 合并操作的时候，Union(a,b)的时候，不是合并a和b，而是将a的根节点和b的根节点进行合并

如图8我们依旧定义一个辅助空间来维护他们的关系，把这个辅助空间叫做parent_id，初始时自己指向自己

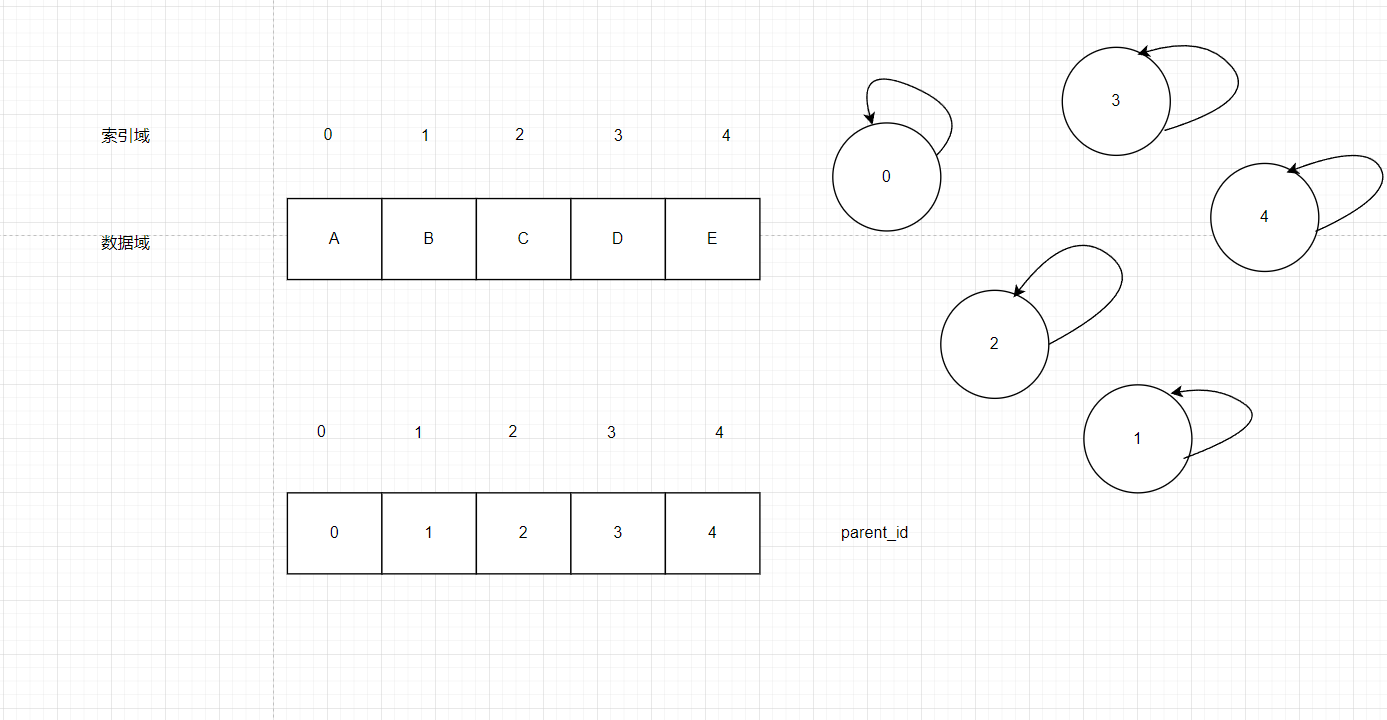
图8

如图9，Union(0,3)就把0指向3，3依旧指向3，我们判断是否是同一集合中就找两个元素最终的父ID是不是同一个就行了，如果指向的是同一个根节点就不需要合并，如果不是就合并，

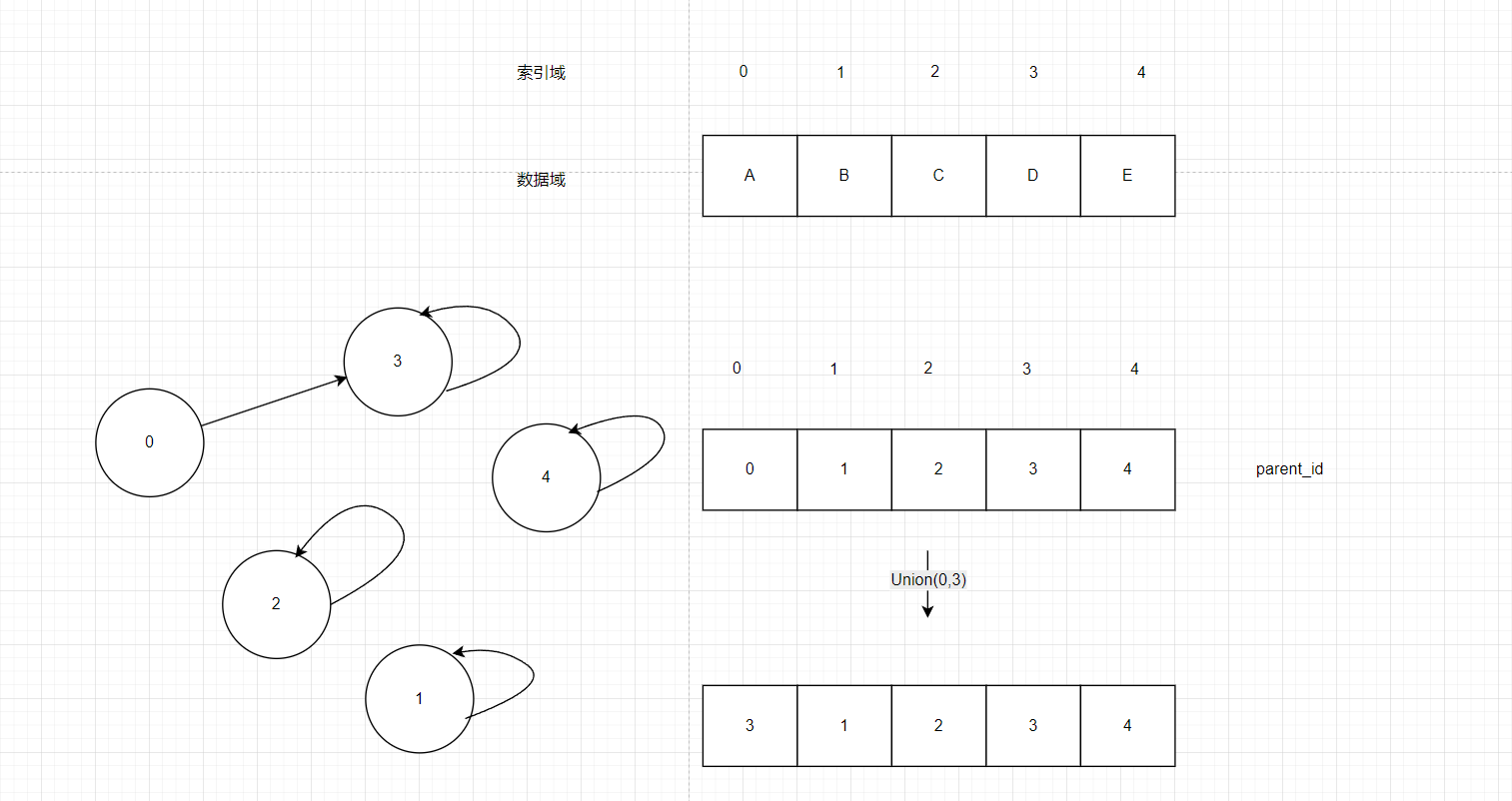
图9

图10就是Union的过程，在执行第三步Union(0,4)的时候就找到 0 和 4 各自的根节点，然后将其中一个根节点的父节点指向另一个根节点，从而把两棵树合并为一棵。

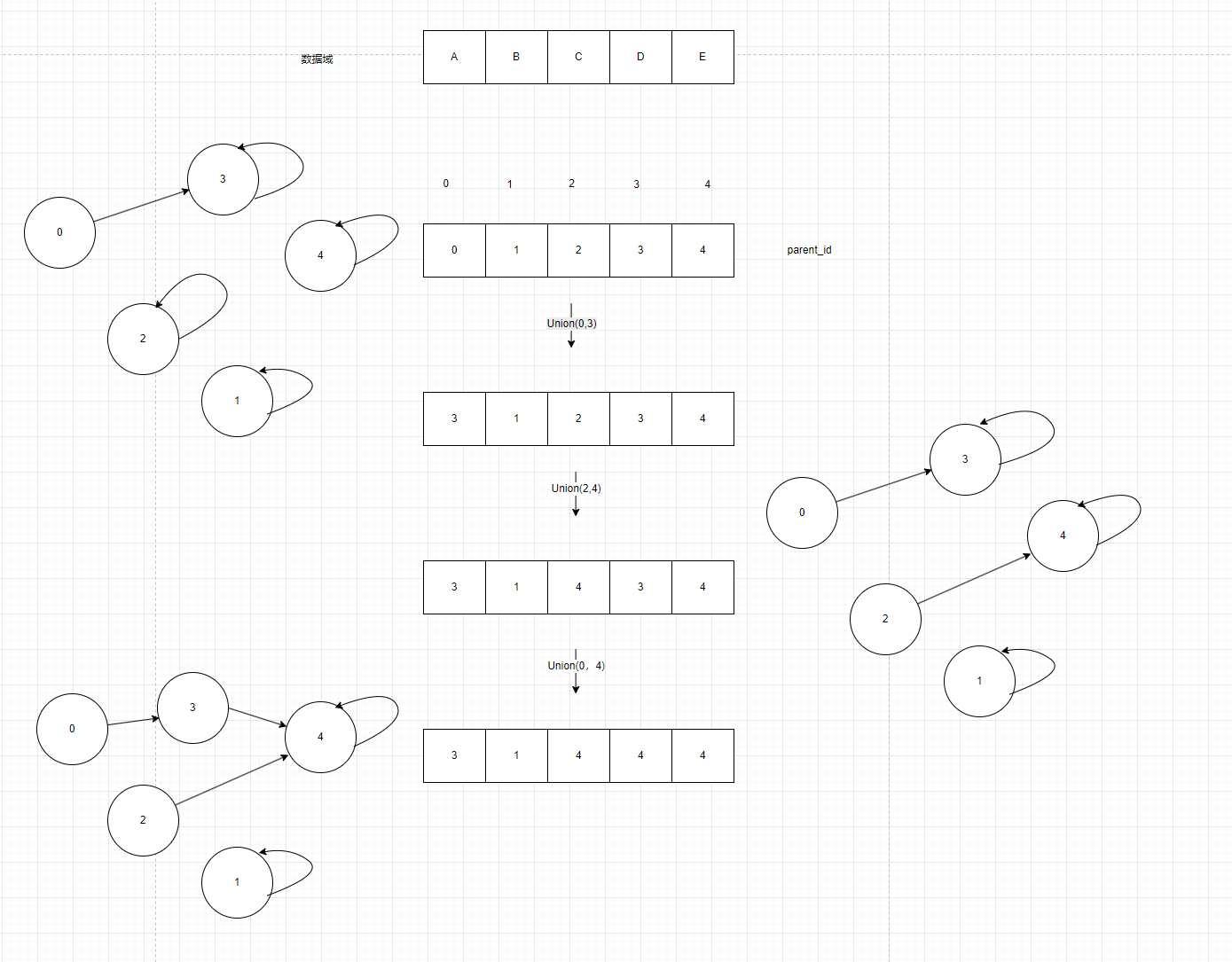
图10

2.2.1Union(x,y)和Find(x,y)的伪代码

• Find(x)​：通过不断查找当前元素的父节点，直到找到根节点（即 parent[x] == x）。这个过程是​沿着父节点向上追溯​。由于查找和树的高度有关，很明显时间复杂度是：O(logN)
• Union(x, y)​：找到 x 和 y 各自的根节点，然后将其中一个根节点的父节点指向另一个根节点，从而把两棵树合并为一棵。时间复杂度也是：O(logN)

2.2.2基于size的算法改进

如图11：在Union的过程中，可能出现不平衡的情况，甚至退化成链表，Union(1,3)

改进方法：将元素少的树嫁接到元素多的树

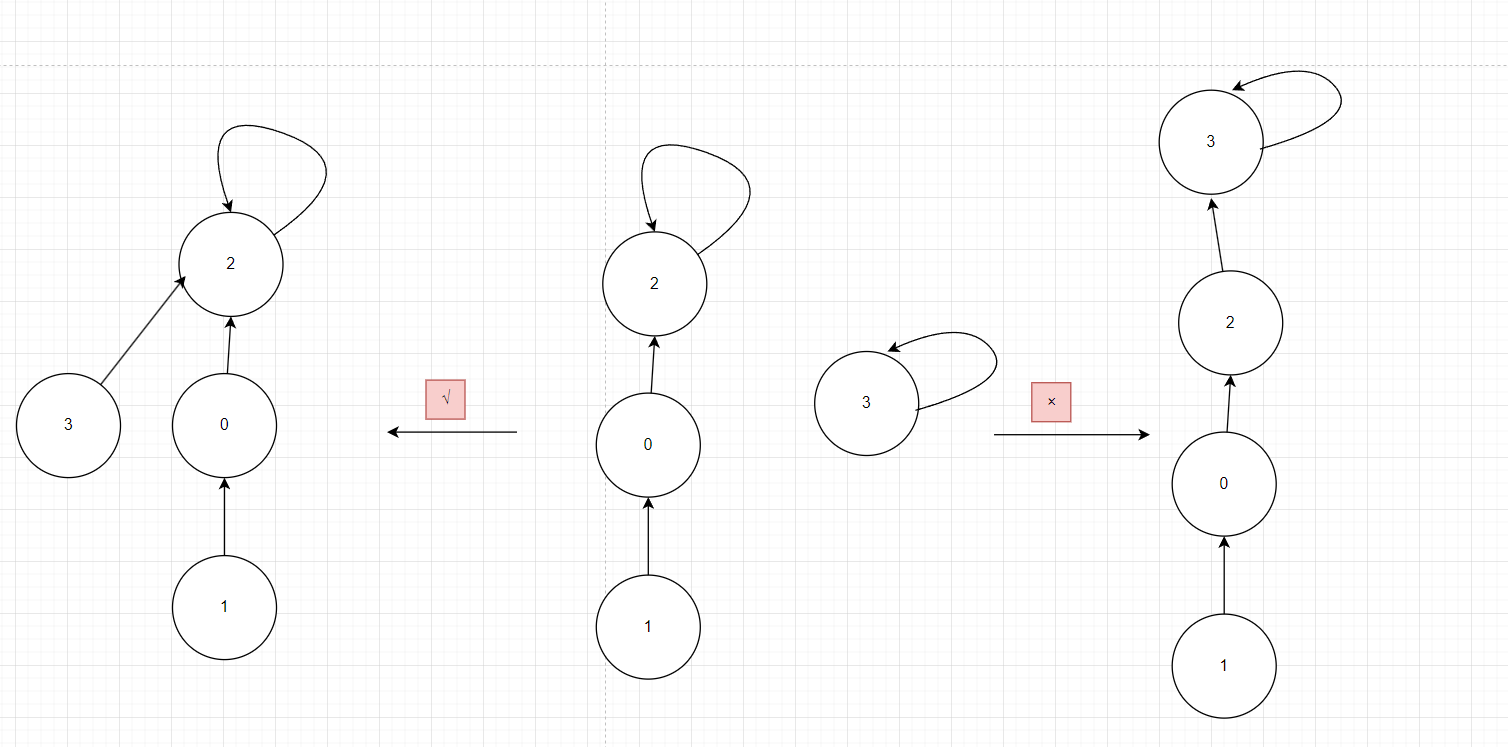
图11

2.2.3基于rank的算法改进

如图12如果按照2.2.2基于rank的算法改进将元素少的树嫁接到元素多的树的话，树的高度反而变高了，这种时候我们应该把矮的树嫁接给高的树

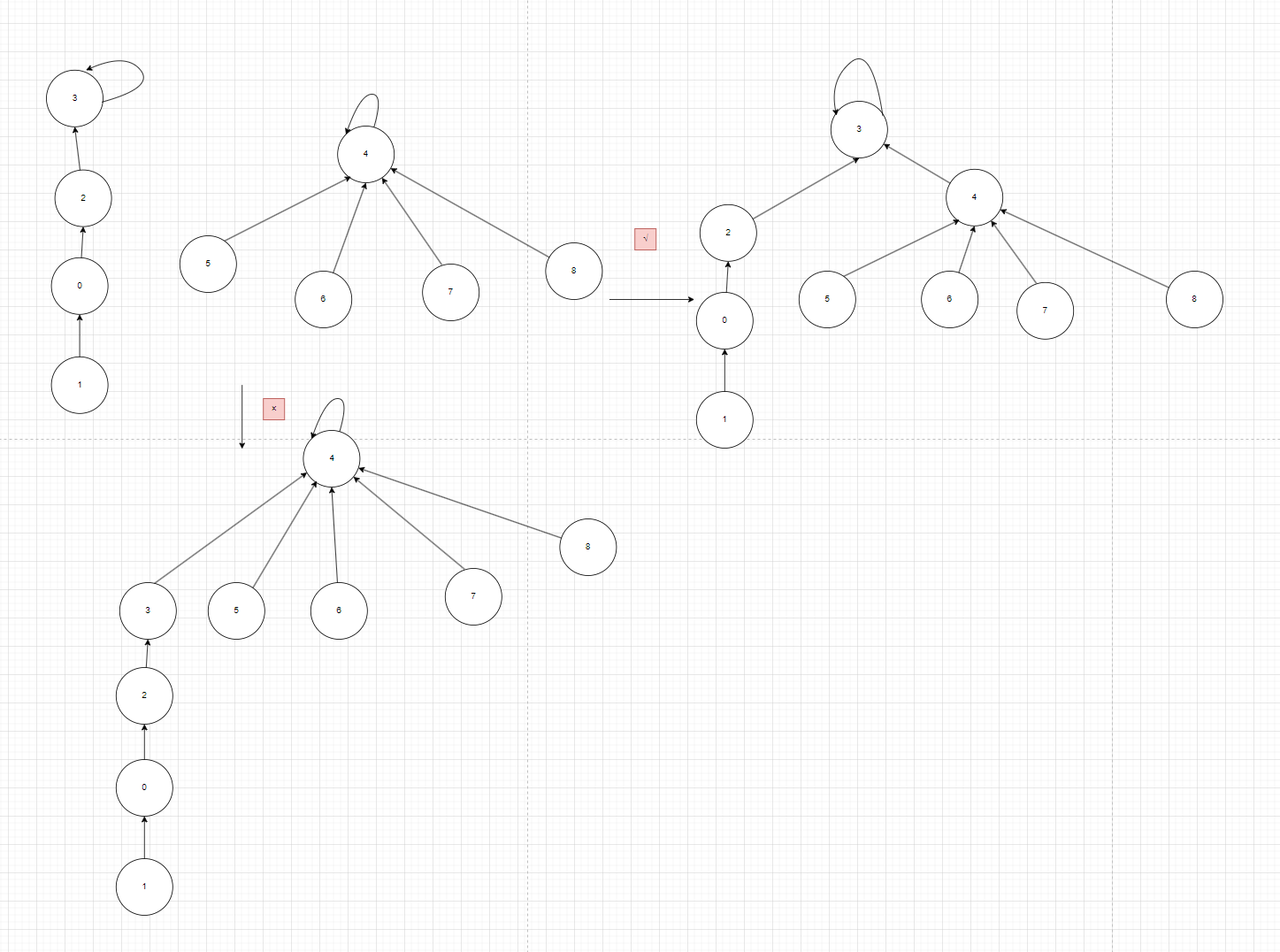
图12

2.2.4路径压缩

在find时使路径上的所有节点都指向根节点，从而降低树的高度，如图13：

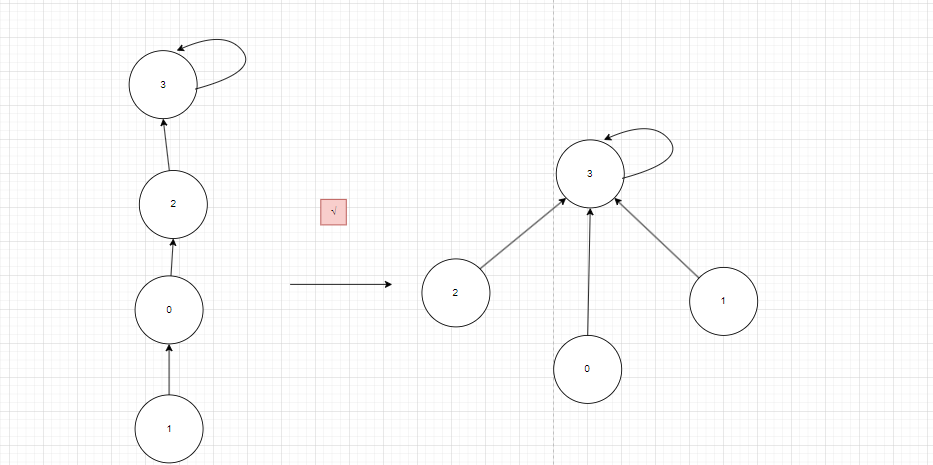
图13

3.QuickFind代码实现

数据结构实现：

typedef int Element;
typedef struct {Element *data;			// 存放具体数据，利用索引来建立数据元素的关系int *groupID;			// 每个元素的组编号，利用索引值找到组ID信息int n;					// 并查集中元素的个数,限制n和groupID的访问
}QuickFindSet;

创建一个QuickFindSet:QuickFindSet *createQuickFindSet(int n);

QuickFindSet * createQuickFindSet(int n) {QuickFindSet *setQF = malloc(sizeof(QuickFindSet));if (setQF==NULL) {fprintf(stderr,"malloc error!!!");return NULL;}setQF->data=malloc(sizeof(Element)*n);setQF->groupID=malloc(sizeof(int) * n);setQF->n=n;return setQF;
}

需要在堆上申请三个空间，一个并查集头，一堆数据空间用来存储真实数据，一堆组ID号用来存放真实数据的组ID，维护数据空间里的数据就在组ID空间内维护。

释放空间:void releaseQuickFindSet(QuickFindSet *setQF) ;

void releaseQuickFindSet(QuickFindSet *setQF) {if (setQF) {if (setQF->data) {free(setQF->data);}if (setQF->groupID) {free(setQF->groupID);}free(setQF);}
}

这里需要释放三个空间注意顺序别反了，要释放sefQF里面的东西，再释放setQF

初始化数据空间和组ID空间:void initQuickFindSet(const QuickFindSet *setQF, const Element *data, int n) ;

void initQuickFindSet(const QuickFindSet *setQF, const Element *data, int n) {for (int i=0; i<n; i++) {setQF->data[i]=data[i];setQF->groupID[i]=i;}
}

是否在一个集合:int isSameQF(QuickFindSet *setQF, Element a, Element b);

static int findIndex(const QuickFindSet *setQF, Element e) {for (int i = 0; i < setQF->n; ++i) {if (setQF->data[i] == e) {return i;}}return -1;
}int isSameQF(QuickFindSet *setQF, Element a, Element b) {int aIndex = findIndex(setQF, a);int bIndex = findIndex(setQF, b);//防越界if (aIndex == -1 || bIndex == -1) {return 0;}return setQF->groupID[aIndex] == setQF->groupID[bIndex];
}

我们需要拿到真实数据的组ID号就要先拿到对应数据空间的索引号所以写了一个内在接口static int findIndex(const QuickFindSet *setQF, Element e)用来获取对应数据空间内的索引号，再用得到的索引号去获得组ID空间内的组ID号，判断两者是否一致。

合并:void unionQF(QuickFindSet* setQF, Element a, Element b);

void unionQF(QuickFindSet* setQF, Element a, Element b) {//data下的indexint aIndex = findIndex(setQF, a);int bIndex = findIndex(setQF, b);if (aIndex == -1 || bIndex == -1) {return;}for (int i = 0; i < setQF->n; ++i) {if (setQF->groupID[i] == setQF->groupID[aIndex]) {setQF->groupID[i] = setQF->groupID[bIndex];}}
}

我们需要拿到真实数据的组ID号,用得到的数据b的组ID号赋值给组ID空间内所有和数据a的组ID号相同的组ID。

4.基于size的算法改进QuickUnion代码实现

数据结构实现：

//基于size的quickUnion
typedef struct {Element *data;			// 存放具体数据，利用索引来建立数据元素的关系int *parent;			// 存父节点int *size;              // 存每棵数的元素多少int n;					// 并查集中元素的个数,限制n和parent的访问
}QuickUnionSet;

创建一个QuickUnionSet:QuickUnionSet *createQuickUnionSet(int n);

QuickUnionSet *createQuickUnionSet(int n) {QuickUnionSet *setQU=malloc(sizeof(QuickUnionSet));if (setQU==NULL) {fprintf(stderr,"setQU malloc failure!!!");return NULL;}setQU->data=malloc(n*sizeof(int));setQU->parent=malloc(n*sizeof(int));setQU->size=malloc(n*sizeof(int));setQU->n=n;return setQU;
}

初始化空间:void initQuickUnionSet(const QuickUnionSet *setQF, const Element *data, int n);

void initQuickUnionSet(const QuickUnionSet *setQF, const Element *data, int n) {for (int i=0;i<n;i++) {setQF->data[i]=data[i];setQF->parent[i]=i;setQF->size[i]=1;}
}

释放空间:void releaseQuickUnionSet(QuickUnionSet *setQU);

void releaseQuickUnionSet(QuickUnionSet *setQU) {if (setQU) {if (setQU->data) {free(setQU->data);}if (setQU->parent) {free(setQU->parent);}if (setQU->size) {free(setQU->size);}free(setQU);}
}

是否在同一集合中:int isSameQU(QuickUnionSet *setQU, Element a, Element b);

static int findIndex(const QuickUnionSet *setQU, Element e) {for (int i = 0; i < setQU->n; ++i) {if (setQU->data[i] == e) {return i;}}return -1;
}static int findRootIndex(const QuickUnionSet* setQU, Element e) {int curIndex = findIndex(setQU, e);if (curIndex == -1) {return -1;}// 向上遍历，直到父节点和自身索引值一致，那么根节点找到while (setQU->parent[curIndex] != curIndex) {curIndex = setQU->parent[curIndex];}return curIndex;
}//拿到元素的下的索引号
//需要不断往父节点走一直走到parent[i]==i;
int isSameQU(QuickUnionSet *setQU, Element a, Element b) {int aRoot = findRootIndex(setQU,a);int bRoot = findRootIndex(setQU,b);if (aRoot == -1 || bRoot == -1) {return 0;}return aRoot==bRoot;
}

我们需要判断传进来的两个数据的根节点是否一致，如果一致则在同一集合，反之。

合并两个集合:void unionQU(QuickUnionSet *setQU, Element a, Element b);

/* 将元素a和元素b进行合并* 1. 找到a和b的根节点，原本是b的父节点指向a的父节点* 2. 引入根节点的size有效规则，谁的元素多，让另外一个接入元素多的组*/
void unionQU(QuickUnionSet *setQU, Element a, Element b) {int aRoot = findRootIndex(setQU, a);int bRoot = findRootIndex(setQU, b);if (aRoot == -1 || bRoot == -1) {return;}if (aRoot!=bRoot) {int aSize=setQU->size[aRoot];int bSize=setQU->size[bRoot];if (aSize<=bSize) {setQU->parent[aRoot] = bRoot;setQU->size[aRoot]+=aSize;}else {setQU->parent[bRoot] = aRoot;setQU->size[aRoot] += bSize;}}
}

注意：由于是基于size的算法改进，需要多加一层判断size的大小。

接下来来看路径压缩的代码，我们需要在findRootIndex的时候，自己写一个栈把路径上的所有节点全存在栈里，当parent[i]==i;后出栈，把出栈的节点指向根节点即可。（用递归写也可以，在归回来的过程中将节点的父指针都指向根节点）

我们采用链式栈来存储：

定义节点：

/* 由于是链式栈，所以需要定义节点 */
typedef struct _set_node {int index;struct _set_node *next;
} SetNode;

由于我们在基于size的quickUnion实现的时候写的数据结构都是一堆连续的空间的首地址，要想在连续空间中找到元素，知道index就可以了，通过index找到对应数据。

static SetNode *push(SetNode *stack, int index) {SetNode *new_node=malloc(sizeof(SetNode));new_node->index=index;new_node->next=stack;return new_node;
}
static SetNode *pop(SetNode *stack, int *index) {SetNode *tmp=stack;*index = stack->index;stack = stack->next;free(tmp);return stack;
}
static int findRootIndex(const QuickUnionSet* setQU, Element e) {int curIndex = findIndex(setQU, e);if (curIndex == -1)return -1;// 找根的路径，经过的所有节点都入栈，直到找到根SetNode *path = NULL;while (setQU->parent[curIndex] != curIndex) {path = push(path, curIndex);curIndex = setQU->parent[curIndex];}// 出栈，将出栈的节点的父指针都指向根节点while (path) {int pos;path = pop(path, &pos);setQU->parent[pos] = curIndex;}return curIndex;
}

在push中我们区别于之前在《01数据结构-顺序栈和链式栈》链接: https://blog.csdn.net/2302_82136376/article/details/149725542?fromshare=blogdetail&sharetype=blogdetail&sharerId=149725542&sharerefer=PC&sharesource=2302_82136376&sharefrom=from_link中写的入栈不一样，那里采用的是C++设计思想，我这里只用于服务这里的代码，直接返回栈顶指针，因为栈压完后没有栈顶什么也完成不了，我们在findRootIndex里先是把path（栈顶指针）设为NULL，不断地push并更新path的值，同理我们在出栈的时候也需要返回栈顶的指针，通过弹出栈顶的指针来将出栈的节点的父指针都指向根节点。

最后来测一下：

#include <stdio.h>
#include "quickFind.h"
#include "quickUnion.h"
void test02() {int n = 9;QuickUnionSet *QUSet= createQuickUnionSet(n);Element data[9];for (int i = 0; i < sizeof(data) / sizeof(data[0]); ++i) {data[i] = i;}initQuickUnionSet(QUSet, data, n);unionQU(QUSet, 3, 4);unionQU(QUSet, 8, 0);unionQU(QUSet, 2, 3);unionQU(QUSet, 5, 6);if (isSameQU(QUSet,0, 2)) {printf("Yes\n");} else {printf("No\n");}unionQU(QUSet, 5, 1);unionQU(QUSet, 7, 3);unionQU(QUSet, 1, 6);unionQU(QUSet, 4, 8);if (isSameQU(QUSet,0, 2)) {printf("Yes\n");} else {printf("No\n");}releaseQuickUnionSet(QUSet);
}
int main() {// test01();test02();
}

结果：

D:\work\DataStruct\cmake-build-debug\02_TreeStruct\UnionFindSet.exe
No
Yes进程已结束，退出代码为 0

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。