图(遍历/最小生成树/单/多源最短路径)
目录
本章采用邻接矩阵进行演示。
一 图的遍历
BFS:
DFS:
二 最小生成树
1. Kruskal
2. Prim
三 单/多源最短路
1. Dijkstra
2. Bellman-Ford
1. Floyd-Warshall
本章采用邻接矩阵进行演示。
一 图的遍历
首先临界矩阵物理上实际是个二维数组,也就是在二维数组中遍历全部的顶点,不管是用迭代还是递归都可以完成所有的顶点遍历。
示例图:
假设有一个图:无向图
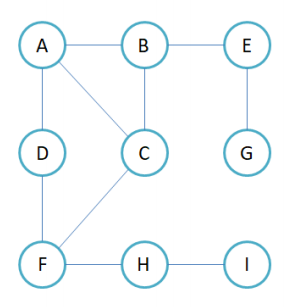
它所对应的物理结构图:
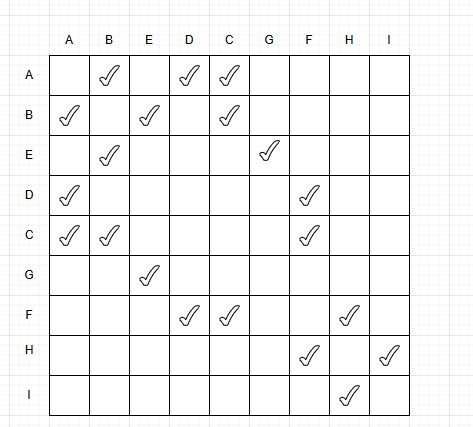
BFS:
首先要遍历全部的点,肯定要给一个点作为起始点来走一遍,所以根据这个点把它连接出去的所有点都保存起来,在让这些保存的点重复同样的操作即可,最后当所有的点都出完即结束。
比如:A 出 B D C,在出 B,此时 B 不能再出 A ,A已经出过要标记一下,也不能再出 C,所以 C入的时候就要标记,所以不管是出过的顶点还是待出的顶点都要标记为不能再次入或者出。
怎么保存与某个顶点相连的边?队列即可。
怎么标记访问过或者待出的顶点?物理结构是数组,可以用下标进行访问,直接用数组标记即可。
什么时候结束?所有的点都被标记或者队列为空即结束。
邻接矩阵结构如下:
class Adjacency_Matrix
{// V 是顶点// E 是权值private:// 根据下标索引顶点vector<V> _v;// 根据顶点索引下标unordered_map<V, int> _index;// 矩阵vector<vector<E>> _matrix;// 标记位vector<bool> _flag;
}代码示例:
void BFS(const V& value)
{// BFS_BFS(value);// 重置标记位for (int i = 0;i < _flag.size();i++)_flag[i] = false;
}
void _BFS(const V& value)
{// 传入错误的顶点直接返回if (_index.find(value) == _index.end())return;queue<int> q;// 队列存入传入的顶点q.push(_index[value]);// 标记该顶点为访问过_flag[_index[value]] = true;// 队列不为空则退出while (!q.empty()){// 取上一个顶点出的所有的顶点的个数int cnt = q.size();while (cnt--){// 依次取该顶点连接的所有的顶点int i = q.front();for (int j = 0;j < _matrix[i].size();j++){if (_matrix[i][j] != 0 && _flag[j] == false){// 如果相邻的顶点没访问过且直接相邻则存放到队列并设置标记位_flag[j] = true;q.push(j);}}// 该顶点取完则弹出q.pop();}}// 如果有的顶点走不到,则遍历标记位数组再次从走不到的顶点开始遍历for (int i = 0;i < _flag.size();i++){if (_flag[i] == false){_BFS(_v[i]);}}
}DFS:
和上面类似,也需要标记数组来标记访问过的顶点,只不过是用递归来完成,
void DFS(const V& value)
{// DFS_DFS(value);// 如果有的顶点走不到,则遍历标记位数组再次从走不到的顶点开始遍历for (int i = 0;i < _flag.size();i++){if (_flag[i] == false){_DFS(_v[i]);}}// 重置标记位for (int i = 0;i < _flag.size();i++)_flag[i] = false;
}
void _DFS(const V& value)
{// 取顶点下标int i = _index[value];// 标记位访问过_flag[i] = true;// 遍历与他连接的顶点for (int j = 0;j < _matrix[i].size();j++){// 如果访问过或者不直接相连则 continueif (_matrix[i][j] == 0 || _flag[j] == true)continue;_DFS(_v[j]);}
}二 最小生成树
在联通图(任意顶点都可以到任意顶点)的情况下:
1. 最小生成树是原始树的子树。
2. 只能用边来构成最小生成树。
3. 只能用 n - 1 条边来构成。
4. 不能带环:比如:A 到 B,B 到 C,C 又到 A,形成环。
所以根据这些规则最小生成树就是用最少的边来构成且不能带环。
1. Kruskal
该算法采用贪心,因为要用最少的边来构成,所以每次都选择全局最小的边来构成最小生成树。
示例图:
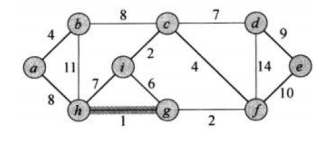
第一步: h -> g。
第二步:g -> f 或者 c -> t。
第三步:g -> f 或者 c -> t。
第四步:c -> f 或者 a -> b。
第五步:c -> f 或者 a -> b。
第六步:h -> i 或者 i -> g 都不能选,因为 i 已经和 h 和 g 间接相连了。
第七步:c -> d。
第八步:a -> h。
第九步:d -> e。
怎么判断是否成环?
并查集可以解决,每次选择一条边就把该边 2 个顶点加入到一个集合即可。
新添加的字段:
typedef Adjacency_Matrix<V, E> self;
// 记录边左右 2 个顶点的连接情况
struct Edge
{int _src;int _des;E _e;Edge(const int& src, const int& des, const E& e):_src(src), _des(des), _e(e){}bool operator<(const Edge& x) const{return _e > x._e;}
};代码示例:
E Kruskal(self& tmp)
{// 生成的最小生成树给 tmpint nn = _v.size();tmp._v = _v;tmp._matrix.resize(nn);tmp._flag.resize(nn);tmp._index = _index;for (int i = 0;i < nn;i++)tmp._matrix[i].resize(nn);// 把所有的边放到优先级队列里,并按小堆存放priority_queue<Edge> pq;for (int i = 0;i < _matrix.size();i++){for (int j = 0;j < _matrix[i].size();j++){if (i < j && _matrix[i][j] != 0){pq.push(Edge(i, j, _matrix[i][j]));}}}// 并查集Disjoint_Set_Data_Structure dsds(_matrix.size());int size = (int)_matrix.size() - 1;int sum = 0;// 选 n - 1 次或者 队列为空则结束while (!pq.empty() && size){// 取最小的边Edge it = pq.top();// 判断边的左右 2 个顶点是否在一个集合if (!(dsds.Is_Gether(it._src, it._des))){// 把边的 左 和 右 放到一个集合里dsds.Merge(it._src, it._des);// 设置进 tmp 里tmp.SetE(_v[it._src], _v[it._des], it._e);// 计算权值和sum += it._e;size--;}// 选完则弹出pq.pop();}// 说明有的边没被选到选不出最小生成树,比如有顶点不和其他任意顶点相连,也就是孤岛if (size != 0)return -1;return sum;
}2. Prim
该算法也采用的是贪心,只不过不是从全局选取最小的边,而是从任意一个顶点开始出发选出最小生成树,开始从传入的顶点开始选择与他直连的顶点权值最小的那个顶点开始连接,后续从最开始出的顶点和后续出的顶点选择出最小的权值边即可。
代码实例:
E Prim(self& tmp, const V& v)
{// 和 Kruskal 一样int nn = _v.size();tmp._v = _v;tmp._matrix.resize(nn);tmp._flag.resize(nn);tmp._index = _index;for (int i = 0;i < nn;i++)tmp._matrix[i].resize(nn);// 并查集Disjoint_Set_Data_Structure dsds(_matrix.size());// 优先级队列和 Kruskal 一样priority_queue<Edge> pq;// 顶点个数int n = _v.size() - 1;// 权值和int sum = 0;// 源点下标int src = _index[v];// 遍历 n - 1 次while (n){// 遍历该顶点所有的边for (int i = 0;i < _matrix[_index[v]].size();i++){int des = i;if (_matrix[src][des] != 0 && (!(dsds.Is_Gether(src, des)))){pq.push(Edge(src, i, _matrix[src][des]));}}// 取最小的那个// 这里最小的那个不一定是最定的顶点出来的,可能是之前的顶点出来的顶点Edge it = pq.top();// 如果选出来的边构成环则弹出继续选while (!pq.empty() && dsds.Is_Gether(it._src, it._des)){pq.pop();it = pq.top();}// 权值累加sum += it._e;// 设置进 tmptmp.SetE(_v[it._src], _v[it._des], it._e);// 弹出选出来最小的边pq.pop();// 合并到一个集合里dsds.Merge(it._src, it._des);// 更新顶点src = it._des;n--;}if (n != 0)return -1;return sum;
}三 单/多源最短路
单源最短路:某一个顶点到任意的顶点权值和最小。
1. Dijkstra
该算法也采用的是贪心算法,和 Prim 算法及其相似,都是从某一个顶点触出发, Prim 则是每次选择最小的边,而 Dijkstra 每次选择从传入的顶点到已确定的顶点权值和最小,该算法只能针对非负权值。
示例图:
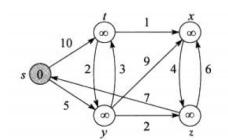
假设 s 是传入的点,从 s 连接出去的边权值和最小的是 y,当然 t 也要更新只不过没有选择 t,后续 t 可能又会被更新成最小的值,在从 y 开始,因为s -> y 这条路径是最短的不会再有其他从 s -> * -> y 最小了,因为没有负权。当 y 出了之后,y 就不用管了,因为 s -> y 的最短路径已经确定了,同样和上面算法一样,访问过的顶点不能在访问了,因为只要访问过了该顶点和源点的最短路径已经确定。
代码示例:
void Dijkstra(const V& v,vector<E>& vertex, vector<int>& parentv)
{// 标记访问过的顶点vector<bool> flag(_v.size());// 存放每个顶点的最短权值和vertex.resize(_v.size(),INT_MAX);// 存放每个顶点的上一个父顶点,因为可能不和源点直接相连parentv.resize(_v.size(),INT_MAX);// 初始化原顶点vertex[_index[v]] = 0;parentv[_index[v]] = _index[v];// 遍历 n 次int size = _v.size();while (size){// 找距离源点和某个顶点权值和最小的那一个int tmp = INT_MAX;E k = INT_MAX;for (int i = 0;i < vertex.size();i++){if (flag[i] == false){if (k > vertex[i]){k = vertex[i];tmp = i;}}}// 找到开始出边并标记为访问过flag[tmp] = true;// 更新出的所有边,这些边可能是默认值也可能是不是默认值但不是最短的也要更新for (int i = 0;i < _matrix[tmp].size();i++){if (flag[i] == false && _matrix[tmp][i] != 0){vertex[i] = min(vertex[i], _matrix[tmp][i] + vertex[tmp]);parentv[i] = tmp;}}size--;}
}2. Bellman-Ford
Dijkstra 是很快的算法,但不能针对负权值,这个算法则可以针对,因为采用的是暴力遍历的方式求最短路径,从源点出发,每次选择任意连接的顶点即可,不需要选择从源点到某个点的最小路径,当所有的点选完之后则再次选择所有的边,因为可能带负权,执行 n - 1次,但如果出现了负权回路则会永远选不出最短路径。
bool BellMan(const V& v, vector<E>& vertex, vector<int>& parentv)
{vertex.resize(_v.size(), INT_MAX);parentv.resize(_v.size(), INT_MAX);vertex[_index[v]] = 0;parentv[_index[v]] = _index[v];// 最多执行 n - 1 次for (int tt = 0;tt < _v.size() - 1;tt++){// 标记是否可以提前退出bool flag = false;// 把每个顶点都走一遍并尝试更新它连接的边for (int kk = 0;kk < _v.size();kk++){// 尝试更新出与他连接的边的最短路径E k = INT_MAX;for (int i = 0;i < _matrix[kk].size();i++){if (_matrix[kk][i] != 0 && vertex[kk] != INT_MAX && _matrix[kk][i] + vertex[kk] < vertex[i]){flag = true;vertex[i] = vertex[kk] + _matrix[kk][i];parentv[i] = kk;}}}// 如果某一次遍历完所有的边都没有进行更新后续的遍历就不可能在出现更新了,则直接退出if (flag == false)break;}// 如果有负权回路则就算执行 n - 1 次也能继续更新,永远都求不出最短路径for (int kk = 0;kk < _v.size();kk++){for (int i = 0;i < _matrix[kk].size();i++){if (_matrix[kk][i] != 0 && _matrix[kk][i] + vertex[kk] < vertex[i]){return false;}}}return true;
}多元最短路:任意顶点到任意顶点权值和最小。
1. Floyd-Warshall
前面 2 个算法针对某个顶点到任意顶点的最短路径,而多元最短路,上面 2 个算法可以把所有顶点都传入进去求最短路径也就是求出任意顶点到任意顶点的最短路径。
该算法采用的是动态规划(二维 dp),用来计算任意顶点到任意顶点的最短路径。
比如:A -> B,可能是直接相连的最短路径,也可能是间接相连的最短 A -> * -> B。
状态转移方程:A -> B = min(A -> B,A -> * -> B)。
和上面 2 个算法不一样,该算法求任意顶点到任意顶点,所以需要二维数组来标记某个顶点到任意顶点的最短权值和,包括路径。
void FloydWarshall(vector<vector<E>>& vertexs, vector<vector<int>>& parentvs)
{// 模拟出和源矩阵一模一样的矩阵int n = _v.size();vertexs.resize(n);parentvs.resize(n);for (int i = 0;i < n;i++){vertexs[i].resize(n, INT_MAX);parentvs[i].resize(n, -1);}// 初始化所有的新矩阵和源矩阵一样for (int i = 0;i < n;i++){for (int j = 0;j < n;j++){if (_matrix[i][j] != 0){vertexs[i][j] = _matrix[i][j];parentvs[i][j] = i;}// 顶点自己和顶点自己额外处理if (i == j){vertexs[i][j] = 0;}}}// 枚举所有顶点可能经过 k 路径for (int k = 0;k < n;k++){// 更新所有的顶点for (int i = 0;i < n;i++){for (int j = 0;j < n;j++){// 求单个顶点到与他相连的顶点的最短路径并尝试更新if (vertexs[i][k] != INT_MAX && vertexs[k][j] != INT_MAX && vertexs[i][k] + vertexs[k][j] < vertexs[i][j]){vertexs[i][j] = vertexs[i][k] + vertexs[k][j];parentvs[i][j] = vertexs[k][j];}}}}
}