当前位置：首页 > java >正文

1-大语言模型—理论基础：详解Transformer架构的实现(1)

java 2025/7/19 9:58:00

1、基于Transformer的编码器和解码器结构

2、依次介绍各个模块的具体功能和实现方法

2.1、嵌入表示层

2.1.1、嵌入表示层（位置编码）

2.1.2、位置编码的工作原理

2.1.3、疑难代码详解

2.1.3.1、计算频率除数

缩放因子

2.1.3.2、添加位置编码

2.1.4、批次维度

2.1.5、为什么位置编码适合作为缓冲区？

1. 缓冲区 vs. 参数的核心区别

2.原因

（1）位置编码是固定的先验知识

（2）需要随模型一起保存和加载

（3）避免污染参数列表

2.1.6、缩放嵌入值

1. 为什么需要缩放嵌入值？

2. 数值不稳定的危害

3. 为什么用 sqrt(d_model) 作为缩放因子？

4. 实例：缩放前后的数值对比

2.1.7、完整代码

2.1.8、实验结果

2.2、注意力层

2.2.1、注意力层（自注意力）

2.2.2、自注意力关键步骤

2.2.2.1、核心公式

2.2.2.2、分步解析

（1）相似度计算：计算 Query 与 Key 的点积

（2）缩放：除以

（3）归一化：应用 Softmax 函数

（4）加权聚合：对 Value 进行加权求和

2.2.3、应用Softmax获取注意力权重

2.2.3.1、注意力权重的本质：“关注概率分布”

2.2.3.2、具体例子：三维张量的 softmax 计算

2.2.3.3、 softmax(dim=-1) 的计算过程

2.2.3.4、为什么必须在 dim=-1 上计算？

2.2.4、完整代码

2.2.5、实验结果

2.3、前馈层

2.3.1、目的

2.3.2、数学公式

2.3.3、作用

（1）引入非线性变换

（2）信息融合与特征增强

（3）提高模型泛化能力

2.3.4、与自注意力机制的互补性

2.3.5、完整代码

后续：2-大语言模型—理论基础：详解Transformer架构的实现(2)-CSDN博客

1、基于Transformer的编码器和解码器结构

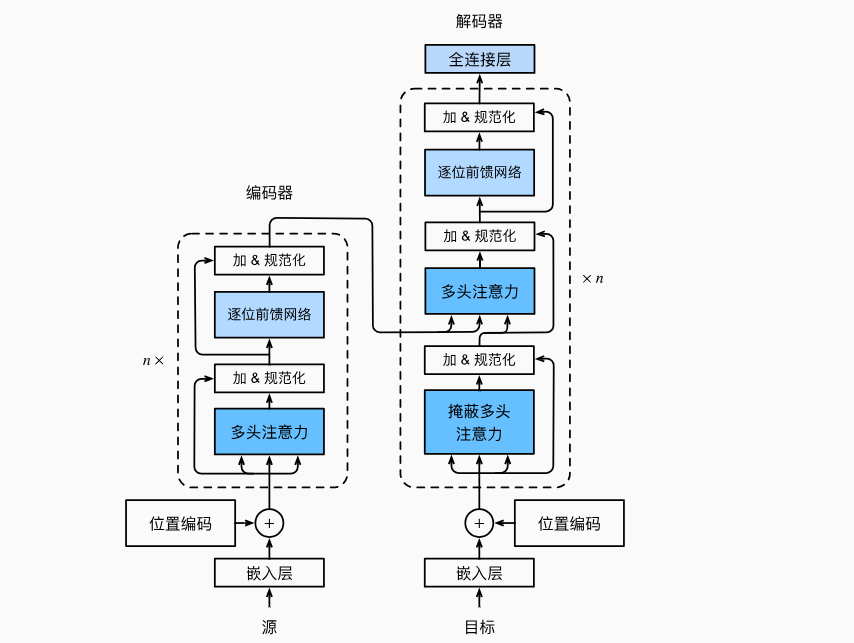
2、依次介绍各个模块的具体功能和实现方法

2.1、嵌入表示层

2.1.1、嵌入表示层（位置编码）

序列中每一个单词所在的位置对应一个向量。这一向量会与单词表示对应相加并送入后续模块中做进一步出来。在训练的过程中，模型会自动学习到如何利用这部分位置信息。

2.1.2、位置编码的工作原理

位置编码通过正弦和余弦函数创建，具有以下特性：

不同频率的函数：

偶数位置使用正弦函数： $PE(pos,2i)=\sin\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right)$
奇数位置使用余弦函数： $PE(pos,2i+1)=\cos\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right)$ 其中， $\text{pos}$ 是位置索引，i 是维度索引， $d_{\text{model}}$ 是嵌入维度。

频率控制：公式中的 $10000^{2i/d_{\text{model}}}$ 控制了不同维度的频率：

低维度（i 较小）：频率低，周期长，捕获长距离位置关系。
高维度（i 较大）：频率高，周期短，捕获短距离位置关系。

相对位置表示：对于任意位置偏移 k， $\text{PE}(\text{pos}+k)$ 可以表示为 $\text{PE}(\text{pos})$ 的线性组合，这使得模型能够学习相对位置关系。

2.1.3、疑难代码详解

2.1.3.1、计算频率除数
div_term = torch.exp(
torch.arange(0, d_model, 2)
.float() 
* (-math.log(10000.0) / d_model)
)
生成维度索引： torch.arange(0, d_model, 2) 生成从 0 开始、步长为 2 的索引序列，即 [0, 2, 4, ...]，对应公式中的偶数维度索引 2i。

转换为浮点数： .float() 将索引序列转换为浮点数类型，确保后续计算精度。

计算缩放因子： -math.log(10000.0) / d_model 计算一个常量缩放因子，其中：

math.log(10000.0) 是 10000 的自然对数（约为 9.21）；
d_model 是模型的总维度数；
负号 - 用于后续指数运算时将基数转换为倒数。

元素 - wise 乘法：将维度索引序列与缩放因子相乘，得到每个维度的指数值： $\text{exponents} = 2i \times \left(-\frac{\ln(10000)}{d_{\text{model}}}\right)$

应用指数函数： torch.exp() 将每个指数值转换为实际的频率除数： $\text{div\_term}[i] = \exp\left(2i \times \left(-\frac{\ln(10000)}{d_{\text{model}}}\right)\right) = \frac{1}{10000^{2i/d_{\text{model}}}}$

缩放因子

将这个公式转换为数值更稳定的形式： $\frac{1}{10000^{2i/d_{\text{model}}}} = \exp\left(2i \times \left(-\frac{\ln(10000)}{d_{\text{model}}}\right)\right)$

分子 2i：维度索引越大，频率除数越小；
分母 $d_{\text{model}}$ ：总维度越大，频率除数衰减越慢。
低维度（i 小）：频率高（周期短），对位置变化敏感，捕捉局部位置关系；
高维度（i 大）：频率低（周期长），对位置变化不敏感，捕捉全局位置关系。
维度 0 的频率除数为 1，周期为 $2\pi$ ，变化最快；
正弦 / 余弦函数将结果约束在 [-1, 1] 内；
若没有缩放，高维度的编码值会趋近于 0，导致信息丢失。

2.1.3.2、添加位置编码
#获取输入序列的实际长度
seq_len = x.size(1) 
#截取对应长度的位置编码并相加
x = x + self.pe[:, :seq_len]
seq_len = x.size(1)：
表示序列的实际长度（即每个样本包含的词元数量），若输入是一个包含 16 个句子的批次，每个句子平均长度为 20，则 x 的形状为 [16, 20, 512]，seq_len 为 20。
x = x + self.pe[:, :seq_len]：
   self.pe 是预计算的位置编码矩阵，通过 register_buffer 注册，形状为 [1, max_seq_len, d_model]（例如 [1, 5000, 512]）。
   [:, :seq_len] 表示截取前 seq_len 个位置的编码，例如：       若输入序列长度 seq_len=10，则截取后的形状为 [1, 10, 512]。
示例：
输入 x 的形状：[4, 10, 512]（4 个样本，序列长度 10，维度 512）
截取的位置编码形状：[1, 10, 512]
广播后位置编码形状：[4, 10, 512]（批次维度复制 4 次） 逐元素相加：x[pos, i] += self.pe[0, pos, i]（对每个位置 pos 和维度 i）广播机制与张量相加
x + self.pe[:, :seq_len] : 
相加后的表示空间
假设词嵌入将 “苹果” 映射到二维空间的点 (0.5, 0.3)，位置编码在第 3 个位置的偏移为 (0.1, -0.2)：相加后：新表示为 (0.6, 0.1)，既保留了 “苹果” 的语义特征，又包含了位置信息；在高维空间中，这种偏移会在每个维度上进行，形成更复杂的位置感知表示。

2.1.4、批次维度

“添加批次维度” 的核心目的是让位置编码矩阵能与批量输入数据兼容：

通过 unsqueeze(0) 在第 0 位增加维度，使 pe 形状从 [max_seq_len, d_model] 变为 [1, max_seq_len, d_model]；
利用 PyTorch 的广播机制，自动适配任意批次大小的输入，确保批量中的每个样本都能正确添加位置编码；
这是高效处理批量数据的标准操作，避免了手动复制数据的冗余计算。

假设 max_seq_len=5，d_model=8，batch_size=2：

初始化 pe：形状 [5, 8]（5 个位置，每个 8 维）；
添加批次维度：pe.unsqueeze(0) → 形状 [1, 5, 8]；
输入词嵌入 x 的形状：[2, 5, 8]（2 个样本，每个 5 个词，每个词 8 维）；
相加时广播：pe 自动扩展为 [2, 5, 8]，与 x 形状匹配，完成逐元素相加。

2.1.5、为什么位置编码适合作为缓冲区？

1. 缓冲区 vs. 参数的核心区别

特性 缓冲区 (Buffer) 参数 (Parameter)
是否参与训练否（不计算梯度）是（计算梯度并更新）
是否随模型保存 / 加载是是
是否在 model.parameters() 中否是
典型用途固定的配置数据、统计量等神经网络权重、偏置等

2.原因

（1）位置编码是固定的先验知识

位置编码矩阵在模型训练前就已确定，不需要通过数据学习。例如：

对于给定的 max_seq_len 和 d_model，位置编码矩阵的计算不依赖训练数据；
在训练过程中，位置编码不需要被优化或更新，因此不需要梯度。

（2）需要随模型一起保存和加载

虽然位置编码不需要训练，但它是模型的一部分。当保存模型时，需要同时保存位置编码矩阵，以确保模型在加载后能正确恢复状态。

（3）避免污染参数列表

如果不使用 register_buffer()，位置编码矩阵会被视为普通的类属性，不会随模型保存。而使用 register_buffer() 可以将其纳入模型状态，但不干扰可训练参数的管理。

特性	缓冲区 (Buffer)	参数 (Parameter)
是否参与训练	否（不计算梯度）	是（计算梯度并更新）
是否随模型保存 / 加载	是	是
是否在 `model.parameters()` 中	否	是
典型用途	固定的配置数据、统计量等	神经网络权重、偏置等

2.1.6、缩放嵌入值

核心目的是避免嵌入向量的数值过大或过小，导致模型训练不稳定（如梯度爆炸 / 消失、收敛缓慢等问题）。

1. 为什么需要缩放嵌入值？

以文本任务为例，输入通常会先经过词嵌入（Word Embedding） 处理：

每个词被映射为一个固定维度的向量（如 d_model=512），这些向量的数值范围通常由初始化方式决定（例如正态分布 N(0, 1)，数值可能在 [-2, 2] 左右）。
当序列较长时，多个嵌入向量的信息会在模型中累积（例如自注意力机制中的加权求和），如果嵌入值本身较大，累积后可能导致张量数值过大（例如超过 1e3）。

2. 数值不稳定的危害

梯度爆炸：若嵌入值过大，后续层的激活值可能急剧增长，导致反向传播时梯度远大于 1，参数更新幅度过大，模型无法收敛。
梯度消失：若嵌入值过小，激活值可能逐渐趋近于 0，反向传播时梯度趋近于 0，参数几乎不更新，模型学习停滞。
数值精度损失：深度学习框架（如 PyTorch、TensorFlow）通常使用 32 位浮点数，过大或过小的数值会超出其精确表示范围，导致计算误差。

3. 为什么用 sqrt(d_model) 作为缩放因子？

假设嵌入向量的每个维度服从均值为 0、方差为 1 的分布，那么嵌入向量的 L2 范数的平方 期望为 d_model（因为 d_model 个方差为 1 的变量之和的期望是 d_model）。
因此，嵌入向量的 L2 范数期望为 sqrt(d_model)。乘以 1/sqrt(d_model) 后，嵌入向量的 L2 范数期望变为 1，将数值范围稳定在合理区间。

4. 实例：缩放前后的数值对比

假设 d_model=512，嵌入向量初始化后的值如下：

缩放前：嵌入向量的 L2 范数可能在 22 左右（因为 sqrt(512)≈22.6）。
缩放后：乘以 1/sqrt(512) 后，L2 范数期望变为 1，数值范围压缩到 [-0.1, 0.1] 左右（假设各维度独立）。

这样，后续层的计算（如自注意力的 Q·K^T）不会因为初始值过大而导致数值爆炸。

2.1.7、完整代码

"""
文件名: 2.1 transformer
作者: 墨尘
日期: 2025/7/18
项目名: LLM
备注:
"""
from tkinter import Variableimport numpy as np
import math
import torch
from sympy.abc import q
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt  # 用于可视化注意力权重热图下·
import torch
import torch.nn as nn
import math
import torch.nn.functional as Fclass PositionalEncoding(nn.Module):def __init__(self, d_model, max_seq_len=80):super().__init__()self.d_model = d_model# 创建位置编码矩阵pe = torch.zeros(max_seq_len, d_model)position = torch.arange(0, max_seq_len, dtype=torch.float).unsqueeze(1)# 计算频率除数div_term = torch.exp(torch.arange(0, d_model, 2) #生成从 0 开始、步长为 2 的索引序列，、最大不超过 d_model-1 的索引序列 即 [0, 2, 4, ...]，对应公式中的偶数维度索引 2i。.float() #将索引序列转换为浮点数类型，确保后续计算精度* (-math.log(10000.0) / d_model)#计算缩放因子)# 应用正弦和余弦函数pe[:, 0::2] = torch.sin(position * div_term)  # 偶数位置使用正弦   从索引 0 开始，每隔 2 个元素取一次（即所有偶数索引）pe[:, 1::2] = torch.cos(position * div_term)  # 奇数位置使用余弦  从索引 1 开始，每隔 2 个元素取一次（即所有奇数索引）# 添加批次维度pe = pe.unsqueeze(0)        #“添加批次维度” 的核心目的是让位置编码矩阵能与批量输入数据兼容：# 通过 unsqueeze(0) 在第 0 位增加维度，使 pe 形状从 [max_seq_len, d_model] 变为 [1, max_seq_len, d_model]；# 注册为缓冲区，不视为模型参数self.register_buffer('pe', pe)def forward(self, x):# 缩放嵌入值以保持数值稳定性x = x * math.sqrt(self.d_model)# 添加位置编码seq_len = x.size(1)   #表示序列的实际长度（即每个样本包含的词元数量）#若输入是一个包含 16 个句子的批次，每个句子平均长度为 20，则 x 的形状为 [16, 20, 512]，seq_len 为 20。x = x + self.pe[:, :seq_len]  #截取对应长度的位置编码并相加return xdef main():"""测试位置编码的基本功能和效果"""# 设置参数d_model = 16  # 模型维度max_seq_len = 5  # 序列长度# 创建位置编码器pos_encoder = PositionalEncoding(d_model, max_seq_len)# 打印位置编码矩阵（前5个位置，前8个维度）print("\n位置编码矩阵 (前5个位置，前8个维度):")print(pos_encoder.pe[0, :5, :8].numpy().round(4))# 验证不同位置的编码差异pos0_encoding = pos_encoder.pe[0, 0]  # 位置0的编码pos1_encoding = pos_encoder.pe[0, 1]  # 位置1的编码# 计算余弦相似度（相似性越低表示差异越大）similarity = torch.cosine_similarity(pos0_encoding.unsqueeze(0),pos1_encoding.unsqueeze(0)).item()print(f"\n位置0与位置1编码的余弦相似度: {similarity:.4f}")if similarity < 0.99:print("✅ 位置编码能有效区分不同位置！")else:print("❌ 位置编码未能有效区分不同位置。")# 测试位置编码对模型的影响（简单示例）# 创建两个相同的嵌入向量，添加不同位置编码embed = torch.randn(1, d_model)embed_pos0 = embed + pos_encoder.pe[0, 0]  # 位置0的嵌入embed_pos1 = embed + pos_encoder.pe[0, 1]  # 位置1的嵌入# 计算欧氏距离（验证添加位置编码后是否不同）distance = torch.norm(embed_pos0 - embed_pos1).item()print(f"\n添加位置编码后的欧氏距离: {distance:.4f}")if distance > 0.1:print("✅ 位置编码成功改变了嵌入向量！")else:print("❌ 位置编码未能有效改变嵌入向量。")if __name__ == "__main__":main()

2.1.8、实验结果

2.2、注意力层

2.2.1、注意力层（自注意力）

自注意力操作是基于Transformer的机器翻译模型的基本操作，在源语言的编码和目标语言的生成中被频繁第使用，以建模源语言和目标语言任意两个单词之间的依赖关系。

自注意力机制涉及的三个元素：查询 $q_{i}$ (Query)、键 $k_{i}$ (Key)和值 $v_{i}$ (Value)。在编码输入序列的每一个单词的表示中，这三个元素用于计算上下文单词对应的权重得分。

2.2.2、自注意力关键步骤

三个关键步骤：相似度计算、权重归一化和加权聚合。以下是详细解析：

2.2.2.1、核心公式

给定输入序列 $X = [x_1, x_2, \dots, x_n]$ ，其中每个 $x_i$ 是维度为 d 的向量，自注意力机制的输出为：

$\text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

其中：

$Q = XW_Q$ ：查询矩阵（Query），形状为 $[n, d_k]$
$K = XW_K$ ：键矩阵（Key），形状为 $[n, d_k]$
$V = XW_V$ ：值矩阵（Value），形状为 $[n, d_v]$
$W_Q$ , $W_K$ , $W_V$ 是可学习的权重矩阵
$\sqrt{d_k}$ ：缩放因子，用于缓解梯度消失问题
$\text{Softmax}$ ：将注意力权重归一化到概率分布

2.2.2.2、分步解析

（1）相似度计算：计算 Query 与 Key 的点积

相似度 $= QK^{T}$

对于每个位置 i 和 j，计算 $\text{sim}(i, j) = q_i^T k_j$ ，表示位置 i 对位置 j 的关注程度。
结果矩阵形状为 $[n, n]$ ，其中每个元素 $(i, j)$ 表示位置 i 对位置 j 的相似度得分。

（2）缩放：除以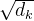 $\sqrt{d_k}$

缩放后相似度 = $\frac{QK^T}{\sqrt{d_k}}$

当 $d_k$ 较大时，点积的方差会增大，导致 Softmax 函数的梯度变得很小（梯度消失）。
缩放因子 $\sqrt{d_k}$ 用于平衡方差，使梯度更稳定。

（3）归一化：应用 Softmax 函数

注意力权重= $\text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)$

将相似度得分转换为概率分布，确保每个位置的注意力权重之和为 1。
公式表示为 $\alpha_{i,j} = \frac{\exp(\text{sim}(i,j)/\sqrt{d_k})}{\sum_{k=1}^n \exp(\text{sim}(i,k)/\sqrt{d_k})}$

（4）加权聚合：对 Value 进行加权求和

输出 = 注意力权重 * V

对于每个位置 i，输出为所有位置 j 的 Value 向量 $v_j$ 的加权和： $\text{output}_i = \sum_{j=1}^n \alpha_{i,j} v_j$

2.2.3、应用Softmax获取注意力权重

2.2.3.1、注意力权重的本质：“关注概率分布”

在自注意力中，我们需要为 每个查询位置 计算一个 对所有键位置的关注概率分布。例如：

当模型处理句子 "I like apples" 时，计算 "like" 这个词应该关注其他哪些词（包括自身）。
理想情况下，"like" 可能会关注 "I"（主语）和 "apples"（宾语），而忽略填充标记或无关词。

2.2.3.2、具体例子：三维张量的 softmax 计算

假设：

batch_size=1（1 个样本）
num_heads=1（1 个头，简化问题）
seq_len=3（序列长度为 3，如句子 "I like apples"）

此时，scores 张量的形状为 [1, 1, 3, 3]，我们可以忽略批次和头维度，直接看最后两个维度 [3, 3]：

# 假设 scores 矩阵如下（忽略 batch 和 head 维度）
scores = torch.tensor([[1.0, 2.0, 3.0],  # 查询位置0（"I"）对键位置0、1、2的得分[4.0, 5.0, 6.0],  # 查询位置1（"like"）对键位置0、1、2的得分[7.0, 8.0, 9.0]   # 查询位置2（"apples"）对键位置0、1、2的得分
])

2.2.3.3、 `softmax(dim=-1)` 的计算过程

softmax(dim=-1) 会 逐行进行归一化，确保每行的和为 1。数学公式为： $\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}$

计算第一行 [1.0, 2.0, 3.0] 的 softmax：

$\text{softmax}([1.0, 2.0, 3.0]) = \left[ \frac{e^{1.0}}{e^{1.0}+e^{2.0}+e^{3.0}}, \frac{e^{2.0}}{e^{1.0}+e^{2.0}+e^{3.0}}, \frac{e^{3.0}}{e^{1.0}+e^{2.0}+e^{3.0}} \right] \approx [0.09, 0.24, 0.67]$

同理，计算第二行 [4.0, 5.0, 6.0] 和第三行 [7.0, 8.0, 9.0]：

$\text{softmax}([4.0, 5.0, 6.0]) \approx [0.09, 0.24, 0.67] \\ \text{softmax}([7.0, 8.0, 9.0]) \approx [0.09, 0.24, 0.67]$

最终得到的注意力权重矩阵：

attn_weights = torch.tensor([[0.09, 0.24, 0.67],  # "I" 对 "I", "like", "apples" 的关注概率[0.09, 0.24, 0.67],  # "like" 对 "I", "like", "apples" 的关注概率[0.09, 0.24, 0.67]   # "apples" 对 "I", "like", "apples" 的关注概率
])

2.2.3.4、为什么必须在 `dim=-1` 上计算？

核心逻辑：每个查询位置（行）需要分配一个 对所有键位置（列）的概率分布，因此必须按行归一化（dim=-1）。

错误示范：如果用 softmax(dim=0)（按列归一化）

# 错误的 softmax(dim=0) 计算（仅作示例，实际不会这样用）
attn_weights_wrong = torch.tensor([[0.00, 0.00, 0.00],  # 第0列的和为1（但这不是我们想要的！）[0.05, 0.05, 0.05],  # 第1列的和为1[0.95, 0.95, 0.95]   # 第2列的和为1
])

这会导致：

每个键位置（列）的权重和为 1，而不是每个查询位置（行）的权重和为 1；
完全违背注意力机制的定义 —— 我们需要的是 “每个查询对所有键的关注分布”，而不是 “所有查询对单个键的关注分布”。

2.2.4、完整代码

"""
文件名: 2.1 transformer
作者: 墨尘
日期: 2025/7/18
项目名: LLM
备注:
"""import numpy as np
import math
import torch
from sympy.abc import q
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt  # 用于可视化注意力权重热图下·
import torch
import torch.nn as nn
import math
import torch.nn.functional as Fclass MultiHeadAttention(nn.Module):"""多头注意力机制模块"""def __init__(self, heads: int, d_model: int, dropout: float = 0.1):"""初始化多头注意力模块参数:heads: 注意力头的数量d_model: 模型的总维度dropout: Dropout概率，默认0.1"""super().__init__()self.d_model = d_modelself.h = headsself.d_k = d_model // heads  # 每个头的维度# 线性投影层：将输入映射到Q、K、V空间# 区分 Q、K、V 的语义角色，明确 “查询 - 键 - 值” 的分工self.q_linear = nn.Linear(d_model, d_model)self.k_linear = nn.Linear(d_model, d_model)self.v_linear = nn.Linear(d_model, d_model)# 输出投影层self.out = nn.Linear(d_model, d_model)# Dropout层self.dropout = nn.Dropout(dropout)#在训练时，nn.Dropout(p) 会以概率 p（默认 p=0.5）随机将输入张量中的部分元素设为 0，# 同时将未被丢弃的元素值放大 1/(1-p) 倍（保证输入的整体期望不变）。# 缩放因子：用于缩放点积注意力的得分，防止梯度消失self.scale = math.sqrt(self.d_k)def attention(self, q: torch.Tensor, k: torch.Tensor, v: torch.Tensor,mask: torch.Tensor = None, dropout: nn.Dropout = None):"""计算注意力得分和输出参数:q: 查询张量，形状 [batch_size, heads, seq_len, d_k]k: 键张量，形状 [batch_size, heads, seq_len, d_k]v: 值张量，形状 [batch_size, heads, seq_len, d_k]mask: 掩码张量，可选，形状 [batch_size, 1, seq_len, seq_len]dropout: Dropout层，可选返回:注意力输出和注意力权重""""""transpose(-2, -1) 表示交换倒数第 2 维和倒数第 1 维：转置后 k 的形状变为 [batch_size, num_heads, d_k, seq_len]交换张量中与 “序列长度” 和 “特征维度” 相关的两个内层维度，使 Q 和 K 的形状满足矩阵乘法的要求（前一个矩阵的列数 = 后一个矩阵的行数），从而正确计算不同位置之间的相似度假设 batch_size=2, num_heads=4, seq_len=5, d_k=16，则：
Q 的形状：[2, 4, 5, 16]
→ 最后两维是 5×16（seq_len × d_k）。
K 的原始形状：[2, 4, 5, 16]
→ 最后两维是 5×16（seq_len × d_k）。
执行 K.transpose(-2, -1) 后：
K 的形状变为 [2, 4, 16, 5]
→ 最后两维是 16×5（d_k × seq_len）。"""# 计算Q和K的点积，得到注意力得分scores = (torch.matmul(q, k.transpose(-2, -1)) #计算 Q 和 K 的点积   转置键张量的最后两个维度/ self.scale) #缩放点积结果# 应用掩码（如果提供）  掩码（Mask）的作用是选择性地 “屏蔽” 某些位置的信息if mask is not None:scores = scores.masked_fill(mask == 0, -1e9)# 应用Softmax获取注意力权重"""假设 seq_len=3，某一个头的 scores 矩阵（忽略 batch 和 heads 维度）为：scores = torch.tensor([[1.0, 2.0, 3.0],  # 查询位置0（"I"）对键位置0、1、2的得分[4.0, 5.0, 6.0],  # 查询位置1（"like"）对键位置0、1、2的得分[7.0, 8.0, 9.0]   # 查询位置2（"apples"）对键位置0、1、2的得分])对 dim=-1（最后一维，即列维度）做 softmax，会将每行的得分归一化：[[0.090, 0.245, 0.665],  # 行内和为1，代表查询0对键0、1、2的注意力权重[0.090, 0.245, 0.665],  # 查询1的权重[0.090, 0.245, 0.665]   # 查询2的权重]attn_weights = torch.tensor([[0.09, 0.24, 0.67],  # "I" 对 "I", "like", "apples" 的关注概率[0.09, 0.24, 0.67],  # "like" 对 "I", "like", "apples" 的关注概率[0.09, 0.24, 0.67]   # "apples" 对 "I", "like", "apples" 的关注概率])"""# 对 dim=-1（最后一维，即列维度）做 softmax，会将每行的得分归一化：attn_weights = F.softmax(scores, dim=-1)  # [batch_size, heads, seq_len, seq_len]# 应用Dropout（如果提供）if dropout is not None:attn_weights = dropout(attn_weights)# 加权聚合值矩阵# torch.matmul() 是用于执行张量矩阵乘法的核心函数output = torch.matmul(attn_weights, v)  # [batch_size, heads, seq_len, d_k]return output, attn_weightsdef forward(self, q: torch.Tensor, k: torch.Tensor, v: torch.Tensor,mask: torch.Tensor = None):"""多头注意力模块的前向传播参数:q: 查询张量，形状 [batch_size, seq_len, d_model]k: 键张量，形状 [batch_size, seq_len, d_model]v: 值张量，形状 [batch_size, seq_len, d_model]mask: 掩码张量，可选，形状 [batch_size, 1, seq_len] 或 [batch_size, seq_len, seq_len]返回:多头注意力输出，形状 [batch_size, seq_len, d_model]注意力权重，形状 [batch_size, heads, seq_len, seq_len]"""batch_size = q.size(0)# 线性投影并重塑为多头结构# [batch_size, seq_len, d_model] -> [batch_size, seq_len, heads, d_k]k = self.k_linear(k).view(batch_size, -1, self.h, self.d_k)q = self.q_linear(q).view(batch_size, -1, self.h, self.d_k)v = self.v_linear(v).view(batch_size, -1, self.h, self.d_k)# 交换维度，便于并行计算多头注意力# [batch_size, seq_len, heads, d_k] -> [batch_size, heads, seq_len, d_k]"""交换前（[seq_len, heads, d_k]）：
[[head1_data_1, head2_data_1],  # 位置1的两个头[head1_data_2, head2_data_2],  # 位置2的两个头[head1_data_3, head2_data_3]   # 位置3的两个头
]
交换后（[heads, seq_len, d_k]）：
[[head1_data_1, head1_data_2, head1_data_3],  # 头1的所有位置[head2_data_1, head2_data_2, head2_data_3]   # 头2的所有位置
]
"""k = k.transpose(1, 2)q = q.transpose(1, 2)v = v.transpose(1, 2)# 调整掩码形状（如果提供）if mask is not None:# 为多头注意力扩展掩码维度# [batch_size, 1, seq_len] -> [batch_size, 1, 1, seq_len]# 或 [batch_size, seq_len, seq_len] -> [batch_size, 1, seq_len, seq_len]mask = mask.unsqueeze(1)# 计算多头注意力output, attn_weights = self.attention(q, k, v, mask, self.dropout)# 重塑并合并多头结果# [batch_size, heads, seq_len, d_k] -> [batch_size, seq_len, heads, d_k]# 重新排列内存布局以确保连续性output = output.transpose(1, 2).contiguous()# [batch_size, seq_len, heads, d_k] -> [batch_size, seq_len, d_model]# x = torch.arange(6)  # tensor([0, 1, 2, 3, 4, 5])# y = x.view(2, 3)     # 重塑为2行3列# 关键限制：# view() 要求张量的内存布局必须是连续的（即元素在内存中按行优先顺序连续存储）。如果张量不连续，调用 view() 会报错。output = output.view(batch_size, -1, self.d_model)# 最终线性投影output = self.out(output)return output, attn_weightsdef main():# 设置参数batch_size = 2       # 批次大小seq_len = 5          # 序列长度d_model = 16         # 模型维度heads = 4            # 注意力头数（需满足 d_model % heads == 0）# 创建随机输入张量（模拟词嵌入）q = torch.randn(batch_size, seq_len, d_model)k = torch.randn(batch_size, seq_len, d_model)v = torch.randn(batch_size, seq_len, d_model)# 创建掩码（可选，这里用全1掩码表示无屏蔽）mask = torch.ones(batch_size, 1, seq_len)  # 形状 [batch_size, 1, seq_len]# 初始化多头注意力模块multi_head_attn = MultiHeadAttention(heads=heads, d_model=d_model)# 执行多头注意力计算output, attn_weights = multi_head_attn(q, k, v, mask)# 打印输入输出形状验证print(f"输入Q形状: {q.shape}")print(f"输出形状: {output.shape}")  # 应与输入形状一致 [batch_size, seq_len, d_model]print(f"注意力权重形状: {attn_weights.shape}")  # [batch_size, heads, seq_len, seq_len]# 验证注意力权重是否有效（每行和为1）head_idx = 0  # 查看第0个头的权重row_sum = attn_weights[0, head_idx, 0].sum().item()  # 第0个样本、第0个头、第0个位置的权重和print(f"\n第0个头第0个位置的权重和: {row_sum:.4f}")  # 应接近1.0# 可视化一个注意力头的权重矩阵（热图）plt.figure(figsize=(6, 6))plt.imshow(attn_weights[0, head_idx].detach().numpy(), cmap='viridis')plt.colorbar(label='注意力权重')plt.title(f'第{head_idx}个头的注意力权重矩阵')plt.xlabel('键位置')plt.ylabel('查询位置')plt.show()if __name__ == "__main__":main()

2.2.5、实验结果

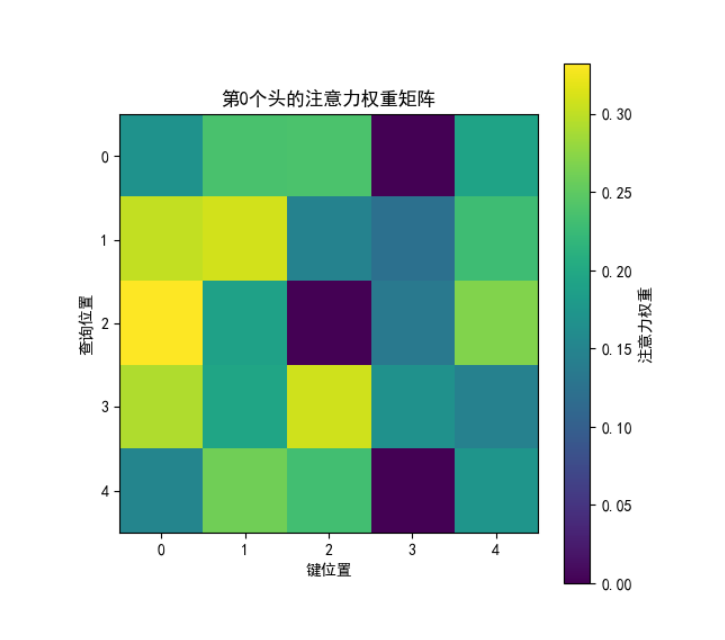
2.3、前馈层

2.3.1、目的

前馈层接收自注意力子层的输出作为输入，并通过一个带有ReLU激活函数的两层全连接网络对输入进行更复杂的非线性变换。（引入非线性变换，增强模型的表达能力，从而捕获更复杂的语义关系）

2.3.2、数学公式

前馈层由两个线性变换（全连接层）和一个 ReLU 激活函数组成，数学表达式如下：

$\text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2$

其中：

x 是自注意力子层的输出，形状为 [batch_size, seq_len, d_model]；
$W_1$ 和 $W_2$ 是可学习的权重矩阵，形状分别为 [d_model, d_ff] 和 [d_ff, d_model]；
$b_1$ 和 $b_2$ 是偏置向量，形状分别为 [d_ff] 和 [d_model]；
$d_{ff}$ 是前馈层的隐藏维度，通常设置为 d_model 的 4 倍（如 d_model=512 时，d_ff=2048）；
$\max(0, \cdot)$ 是 ReLU 激活函数，引入非线性特性。

2.3.3、作用

（1）引入非线性变换

自注意力机制主要通过线性变换和点积操作捕获序列间的依赖关系，但线性操作的表达能力有限。前馈层通过 ReLU 激活函数引入非线性，使模型能够学习更复杂、更抽象的模式。

（2）信息融合与特征增强

前馈层将自注意力子层输出的特征映射到更高维空间（通过 $W_1$ 扩展到 $d_{ff}$ 维），然后再投影回原始维度（通过 $W_2$ 收缩到 $d_{\text{model}}$ 维）。这种 “扩展 - 收缩” 结构允许模型在高维空间中融合信息，提取更丰富的特征表示。

（3）提高模型泛化能力

两层全连接网络加 ReLU 激活的结构增加了模型的复杂度，同时保持了参数量的可控性。这使得模型能够在不同任务中泛化得更好，避免过拟合。

2.3.4、与自注意力机制的互补性

组件	核心功能	非线性	捕获关系类型
自注意力	捕获序列间的长距离依赖关系	否	全局位置关联
前馈层	对每个位置的特征进行非线性变换	是	局部特征增强

前馈层与自注意力机制相辅相成：

自注意力机制关注 “哪些位置相关”，解决序列中的依赖问题；
前馈层关注 “如何转换这些相关信息”，增强特征表达能力。

2.3.5、完整代码


# -------------------------- 1. 基于位置的前馈网络（PositionWiseFFN） --------------------------
# 作用：对序列中每个位置的特征向量独立进行非线性变换，增强模型对局部特征的表达能力
# 地位：Transformer中注意力机制后必接的子层，为特征添加非线性交互
class PositionWiseFFN(nn.Module):"""基于位置的前馈网络（Transformer子层）"""def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs, **kwargs):"""初始化前馈网络参数详解:ffn_num_input: 输入特征维度（需与注意力机制输出维度一致）ffn_num_hiddens: 隐藏层维度（通常大于输入维度，形成"升维-降维"结构）ffn_num_outputs: 输出特征维度（需与输入维度一致，才能参与残差连接）"""super(PositionWiseFFN, self).__init__(** kwargs)self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)  # 第一层线性变换（升维）self.relu = nn.ReLU()  # 非线性激活函数，引入特征间的交互self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)  # 第二层线性变换（降维）def forward(self, X):"""前向传播：对序列中每个位置的特征独立应用相同的MLP参数:X: 输入张量，形状为(batch_size, seq_len, feature_dim)（batch_size：样本数；seq_len：序列长度）返回:输出张量，形状与X一致（保持序列长度和样本数，仅特征维度经非线性变换）"""# 计算流程：输入 → 升维（增加特征交互能力） → 非线性激活（引入非线性） → 降维（恢复原特征维度）return self.dense2(self.relu(self.dense1(X)))