当前位置：首页 > java >正文

7.17 滑动窗口 |assign |memo |pii bfs

java 2025/7/17 15:59:05

lc1129.bfs
queue<pii>的抽象
和vis[node][color]的check

class Solution {
typedef pair<int, int> pii;
vector<vector<pii>> g;
int n = 0;
public:
vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& redEdges, vector<vector<int>>& blueEdges) {
this->n = n;
g.resize(n);

for (auto& e : redEdges)
g[e[0]].push_back({e[1], 0});
for (auto& e : blueEdges)
g[e[0]].push_back({e[1], 1});

vector<int> ans(n, -1);
ans[0] = 0;
for (int i = 1; i < n; i++) {
ans[i] = bfs(0, i);
}
return ans;
}

int bfs(int start, int end) {
queue<pair<int, int>> q;
vector<vector<bool>> vis(n, vector<bool>(2, false));
q.push({start, -1});
int ret = 0;

while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
auto [curNode, lastC] = q.front();
q.pop();

if (curNode == end) {
return ret;
}

for (auto [nextNode, edgeC] : g[curNode]) {
if ((lastC == -1 || edgeC != lastC) && !vis[nextNode][edgeC]) {
vis[nextNode][edgeC] = true;
q.push({nextNode, edgeC});
}
}
}
ret++;
}
return -1;
}
};

lc765.
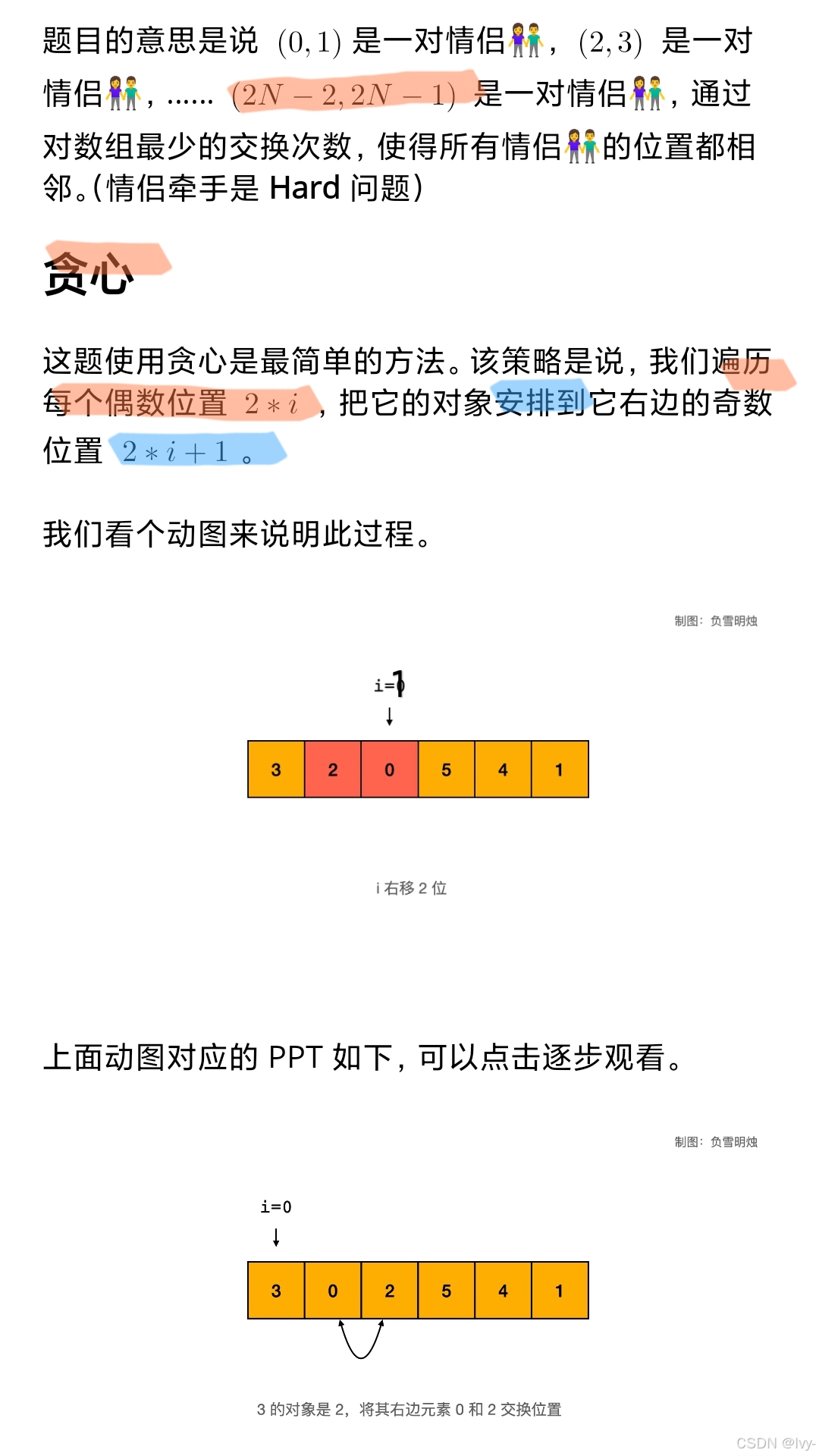
贪心，i+=2的移动
即遍历2i，check 安排保证2*i+1 换到正确位置

class Solution {

public:

int minSwapsCouples(vector<int>& row) {

int n = row.size();

unordered_map<int, int> h;

for (int i = 0; i < n; i++)

h[row[i]] = i;

int res = 0;

for (int i = 0; i < n; i += 2) {

int x = row[i];

int p = x % 2 ? x - 1 : x + 1;

if (row[i + 1] != p) {

res++;

int pos = h[p];

int t = row[i + 1];

row[i + 1] = p;

row[pos] = t;

h[t] = pos;

h[p] = i + 1;

}

return res;

}

};

lcp56. memo优化tle
或者改用bfs

class Solution {

int m, n;

int dx[4] = {0, 0, 1, -1};

int dy[4] = {1, -1, 0, 0};

public:

int conveyorBelt(vector<string>& matrix, vector<int>& start, vector<int>& end)

{

int ret = INT_MAX;

m = matrix.size();

n = matrix[0].size();

vector<vector<bool>> vis(m, vector<bool>(n, false));

vis[start[0]][start[1]] = true;

function<void(int, int, int)> dfs = [&](int a, int b, int cnt)

{

if(cnt>=ret) return;

if (a == end[0] && b == end[1])

{

ret = min(ret, cnt);

return;

}

for (int k = 0; k < 4; k++)

{

int x = a + dx[k], y = b + dy[k];

if (x >= 0 && y >= 0 && x < m && y < n && !vis[x][y])

{

int op = cnt;

if (check(k) != matrix[a][b])

op++;

vis[x][y] = true;

dfs(x, y, op);

vis[x][y] = false;

}

};

dfs(start[0], start[1], 0);

return ret;

}

char check(int k)

{

if (k == 0) return '>';

if (k == 1) return '<';

if (k == 2) return 'v';

return '^';

}

};

lc3015.
法1：暴力bfs，数据范围only 100，可以过

法2：加入了x,y，可以思考加入的x,y影响了什么呢? 通过数学找规律

class Solution {
public:
vector<int> countOfPairs(int n, int x, int y) {
vector<int> ret(n, 0);
for (int i = 1; i <= n; ++i) {
for (int j = i + 1; j <= n; ++j) {
// 计算三种可能路径的最短距离
int direct = j - i;
int viaX = abs(i - x) + 1 + abs(j - y);
int viaY = abs(i - y) + 1 + abs(j - x);
int minDist = min({direct, viaX, viaY});
ret[minDist - 1] += 2;
}
}
return ret;
}
};

assign

assign 是容器（比如 vector）的一个接口

作用：清空容器原来的内容，然后放入新的元素。

打个比方，就像你有一个盒子， assign(n, false) 就相当于：

- 先把盒子里原来的东西全倒掉
- 再往盒子里放 n 个 false

这样能确保容器里的内容是全新的，不会有之前残留的数据，避免出错。

lc523.同余定理
两个注意点
同余定理：余数相同的两个数，做差可被整除。--前缀和
hash存mod，不可以用set，因为要保证len大于等于2，所以要存idx映射
！！还有对于全选和全不选的两个边界，下标初始化处理

同余定理就是说：两个整数 a 和 b，如果除以同一个正整数 m 后余数相同，就称 a 和 b 对 m 同余，简单记成 a ≡ b (mod m) ，大白话就是“除以 m 剩得一样” 。

比如 17 和 5 除以 6 都余 5，就说 17 和 5 对 6 同余。则(17-5)%6=0，余数相同的两个数，做差可被整除。

class Solution {
public:
bool checkSubarraySum(vector<int>& nums, int k)
{
int n=nums.size();
vector<int> f(n+1,0);

for(int i=0;i<n;i++)
{
f[i+1]=f[i]+nums[i];
}
unordered_map<int,int> hash;
hash[0]=0;

for(int i=0;i<=n;i++)
{
int mod=f[i]%k;

if(hash.count(mod))
{
if(i-hash[mod]>=2)
return true;
}
else
hash[mod]=i;
}
return false;

}
};

lc1423.
滑动窗口➕正难则反(用滑动窗口，就要转化为连续部分才能滑～)

取两边最大->转化为中间最小

喜提tle....

class Solution {
vector<int> card;
int n=0,k=0,ret=0;
public:
int maxScore(vector<int>& cardPoints, int k)
{
card=cardPoints;
this->k=k;
n=cardPoints.size();
dfs(0,n-1,0,0);

return ret;
}

void dfs(int b,int e,int sum,int cnt)
{
if(cnt==k)
{
ret=max(ret,sum);
return;
}

dfs(b,e-1,sum+card[e],cnt+1);
dfs(b+1,e,sum+card[b],cnt+1);
}
};