6.3.1图的广度优先遍历
知识总览
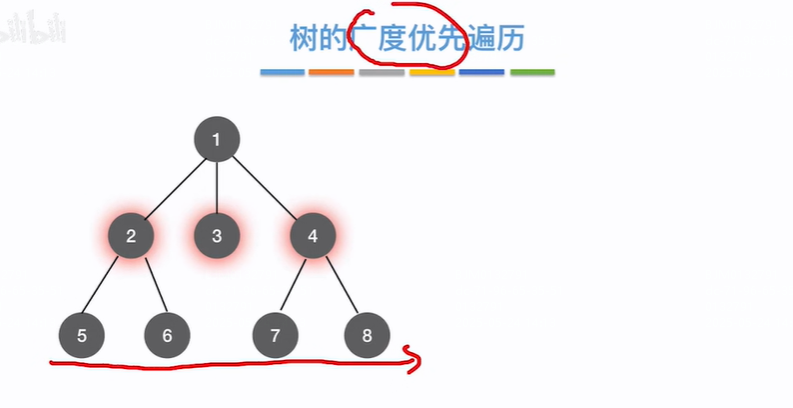
树的广度优先遍历(层次遍历)
从根节点出发,找到和根节点相邻的2、3、4,再找和2、3、4相邻的5、6、7、8,一层层找
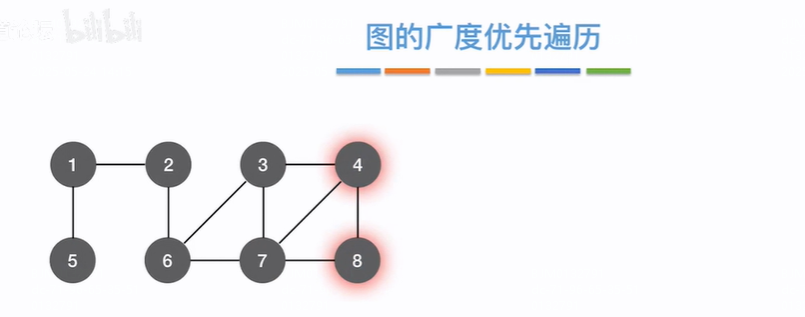
图的广度优先遍历
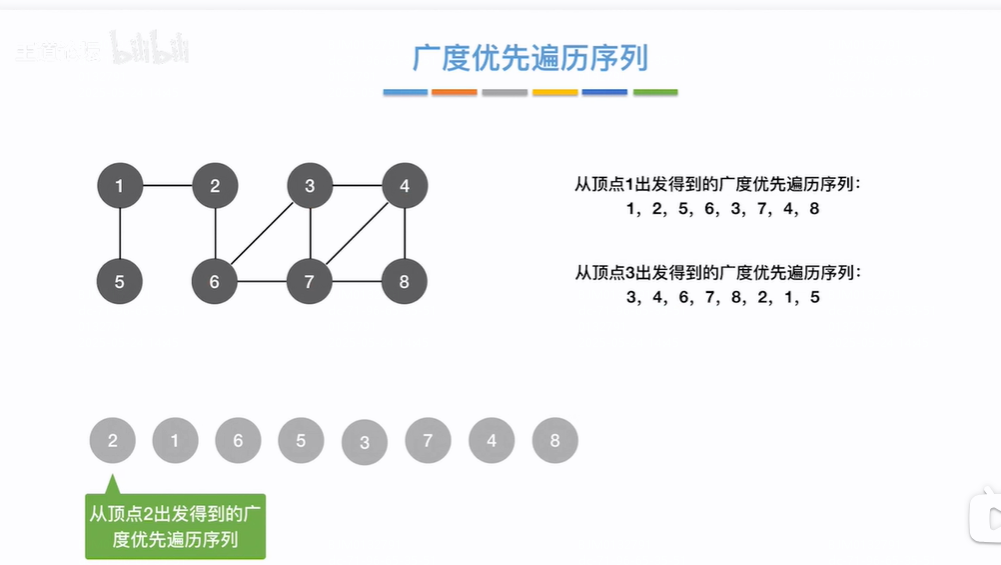
假设从2出发,先找和2相邻的1、6,再找和1、6相邻的5、3、7,再找和5、3、7相邻的4、8
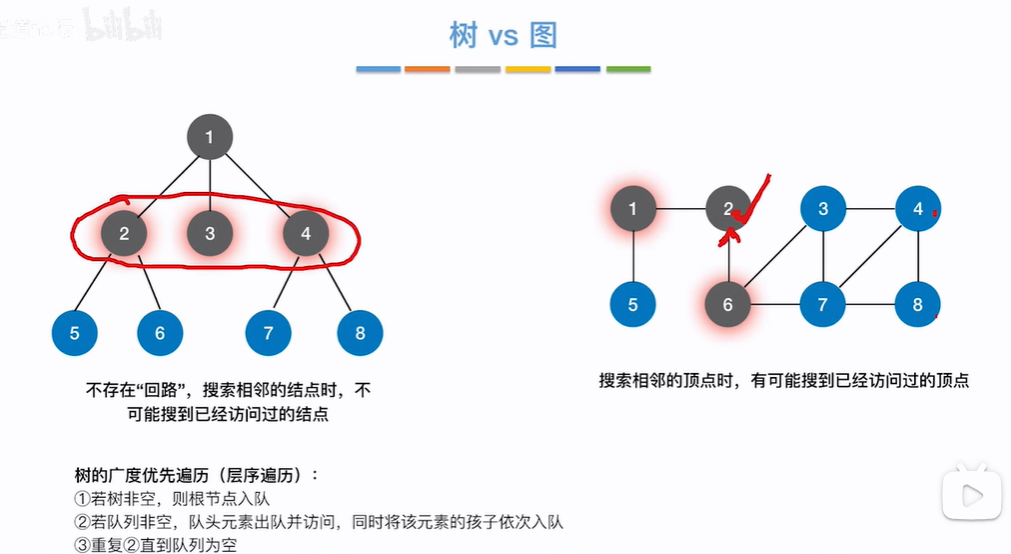
树和图对比
树没有环,所以按层访问一个个节点时不会访问到相同的节点,图有环,从某个节点开始依次找相邻节点时可能找到已经被访问的节点,因此为了让某个节点只被访问一次,在图访问时可以给节点打上标志表示是否已经被访问过
计算机中处理某一层的相邻节点时是一个个节点的相邻节点处理的,即如下树图在找2、3、4这一层的相邻节点时,只能先处理2的相邻节点再依次处理3、4节点的相邻节点,开始没被处理到的节点先放到一个辅助队列,图类似。
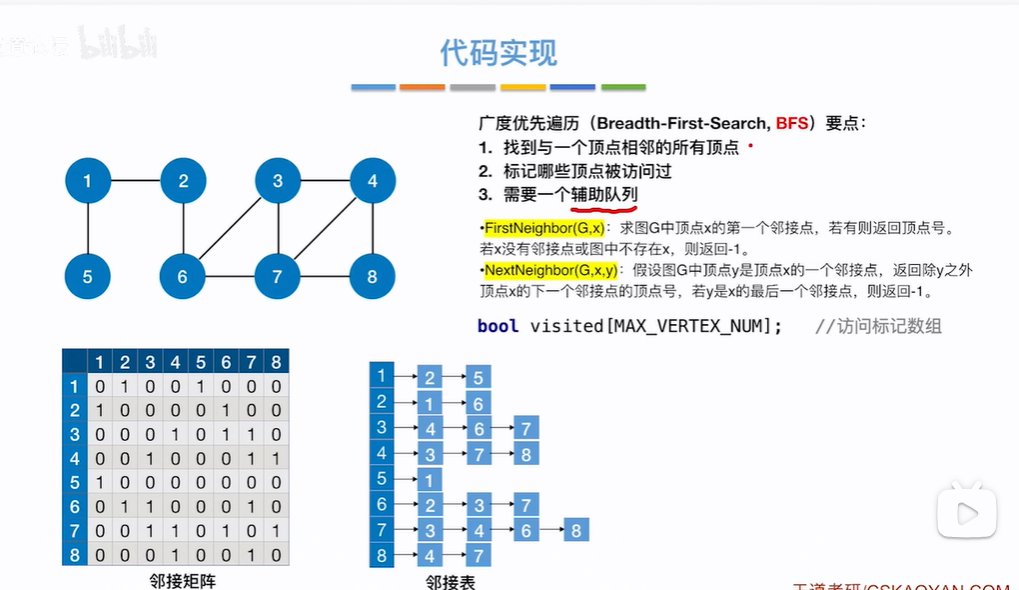
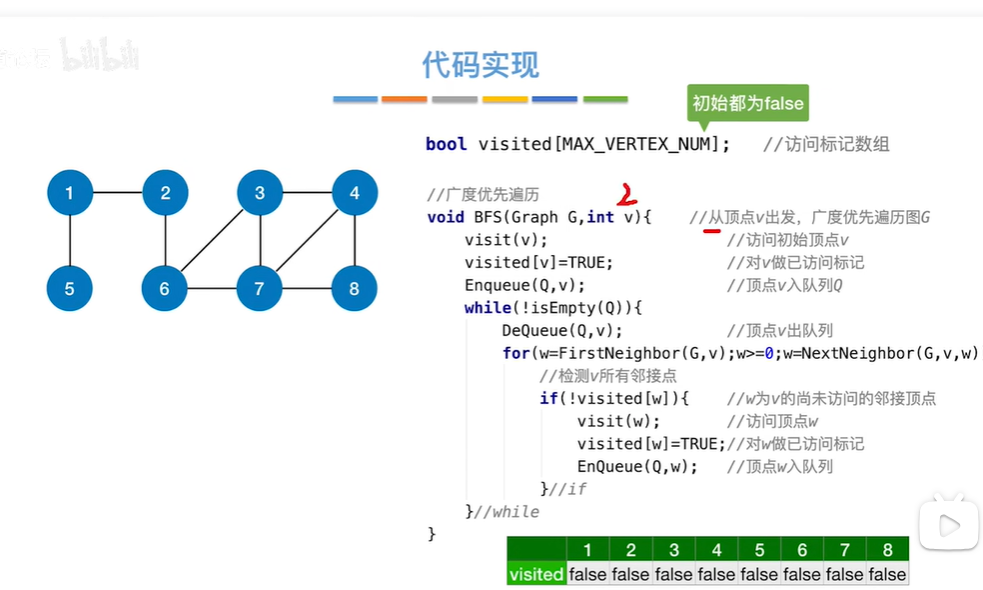
代码实现图的广度优先遍历
使用firstNeighbor找到x顶点的第一个邻接点(咋算第一个邻接点??),再使用NextNeighbding找到其他邻接点,依次就会找到x的所有邻接点,用visited数组来标识已经被访问的节点
过程如下:
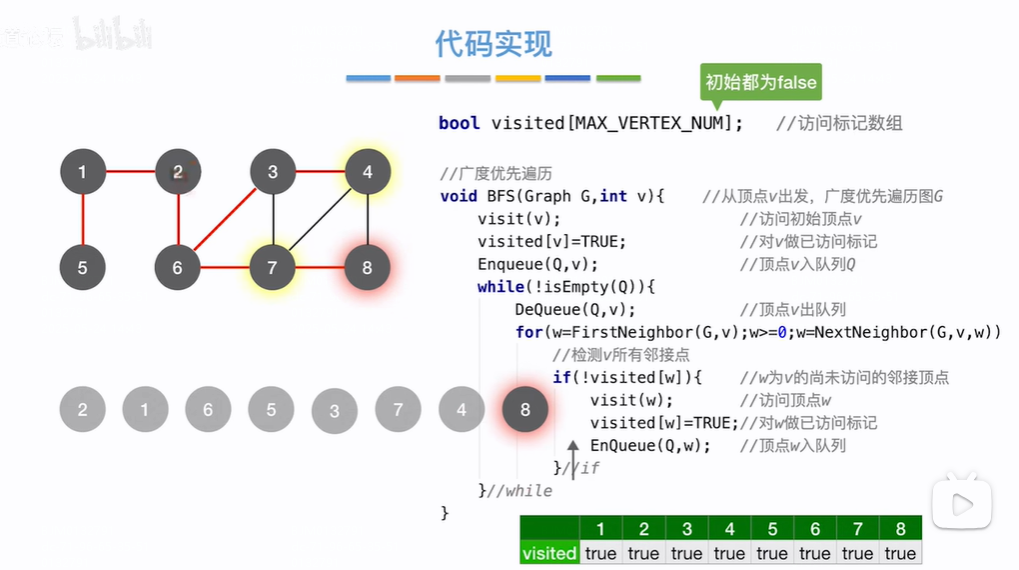
开始visited数组都为false,即各个节点都没访问(visited数组长度为节点数量)。假设从顶点2出发,先访问2顶点,访问了之后该节点对应visited数组上下标=true(数组下标都从0开始,视频上2节点对应了下标2应该只是为了讲清楚原理),2节点入队(开始辅助队列为空,所以2入队之后既是在队头也是在队尾),然后while循环判断队列是否为空,不为空头指针指向元素出队,即2节点出队,估摸DeQueue(Q,v)返回v=2,去for循环查找该队头元素2邻接点,第一次循环w=firstNeighbor(G,2)=1,1节点未被访问,则访问1顶点,然后visited[1]=true,1节点入队,即现在队列为空队列,1既为头节点又是尾结点,第二次循环w=NextNeighbor(G,2,1)=6,6未被访问访问6顶点,visited[6]=true,6入队放到队尾,此时头节点还是1,2没有其他邻接点了for循环结束,此时Q队列不为空,进行第二轮while循环,头结点元素出队,即v=1(此时头节点指向6),for循环找1的邻接点,w=firstNeighbor(G,1)=5,5未被访问,访问5并设置visited[5]=true,5入队放到队尾,1没有其他邻接点for循环结束,Q现在有2个元素6和5,Q不为空头结点元素出队,即v=6(此时头结点指向5),找6的邻接点即w=firstNeighbor(G,6)=2,2在visited[2]=true已被访问不再访问,则w=nextNeighbor(G,6,2)=3,访问3设置visited[3]=true,3入队放到队尾,继续w=nextNeighbor(G,6,3)=7(为啥能返回7不是2??),7被访问并visited[7]=true,7入队放到队尾,Q中此时有5、3、7节点,头指针指向5,继续下一轮出队for循环操作,,,,,,,,直到队列为空(所有的节点在当前while循环中都被访问了,访问的是它的邻接点,如果邻接点为空,证明所有的节点都被访问了,所有入队的都是被访问过的)
从顶点1出发,1先入队,Q=(1),1的邻接点是2和5,1出队2先入队为Q队列头节点,即Q=(2,5),2的邻接点是1和6,1被访问6入队(所有节点找邻接点的时候该节点都已出队),Q=(5,6),5的邻接点没有,则Q=(6),6的邻接点是2、3、7,2被访问,3、7入队,Q=(3,7),3的邻接点是6、7、4,6、7被访问,4入队,Q=(7,4),7的邻接点是6、3、4、8,6、3、4被访问,8入队,Q=(4,8),4的邻接点是3、7、8都被访问已入队过,不再入队,8的邻接点是4、7都被访问已入队过不再入队,此时Q为空跳出while循环,即整个序列(Q队列)依次为1,2,5,6,3,7,4,8
从顶点3出发,3先入队,Q=(3),3的邻接点是6、7、4,3出队4先入队为Q队列头节点(让6、7、4这三个节点谁先入队顺序不一定,目前先根据邻接矩阵即节点号递增的顺序入队,如果是邻接表就不一定是4先入队了),即Q=(4,6,7),4的邻接点是3、7、8,3、7被访问8入队,Q=(6,7,8),6的邻接点是2、3、7,3、7已被访问不入,2入队则Q=(7,8,2),7的邻接点是6、3、4、8,6、3、4、8被访问不入队,Q=(8,2),8的邻接点是4、7、,4、7被访问不入队,Q=(2),2的邻接点是1、6,6被访问不入队1入队,Q=(1),1的邻接点是2、5,2被访问不入队5入队,Q=(5),5的邻接点是1,1被访问不入队,此时Q为空跳出while循环,即整个序列(Q队列)依次为3,4,6,7,8,2,1,5
采用邻接矩阵的方式遍历序列唯一根据节点编号递增顺序访问,因为邻接矩阵是唯一的
采用邻接表的方式遍历序列不唯一
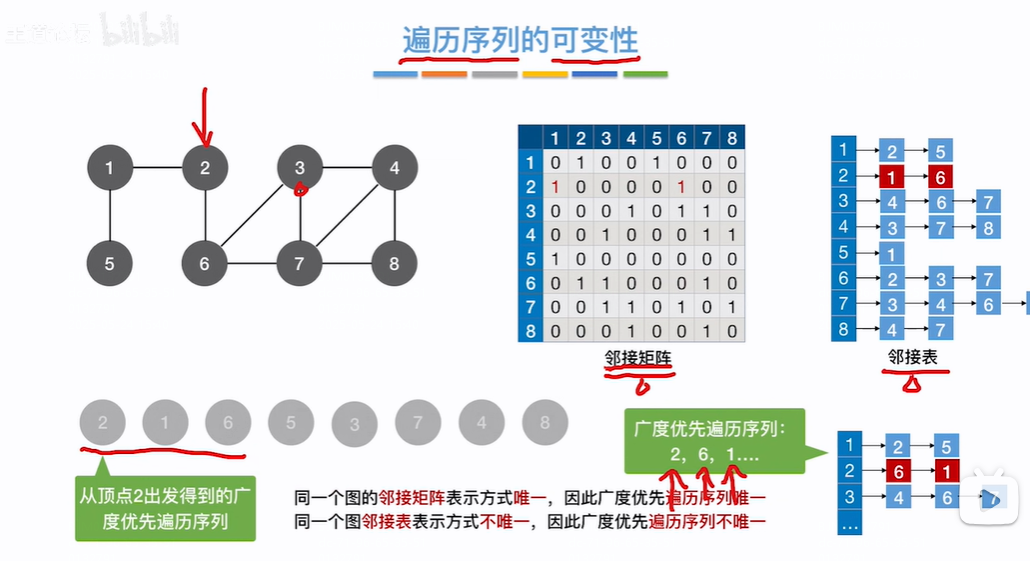
广度优先遍历-优化版
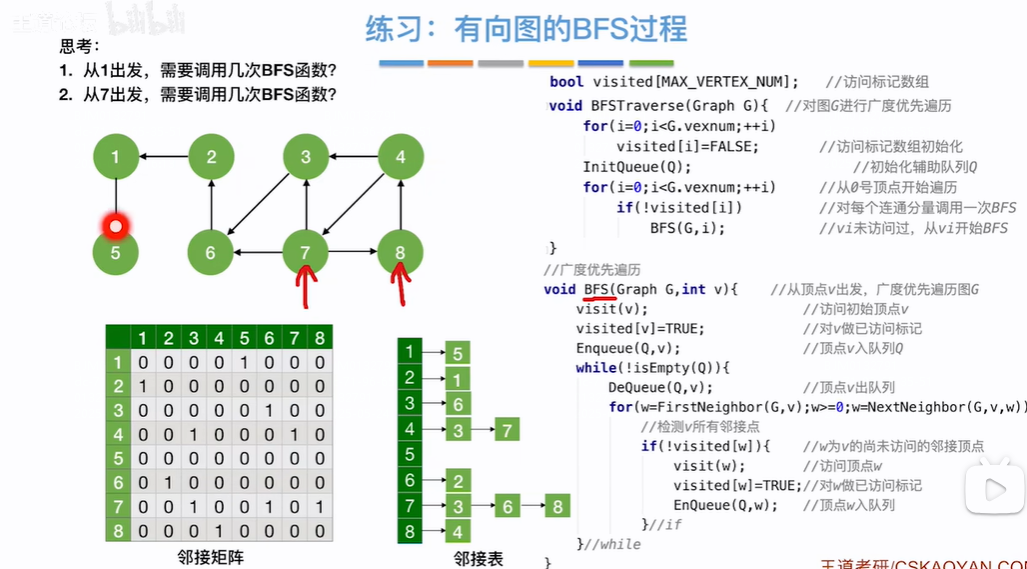
代码缺点:如果是非连通图的形式,从某个节点出发,有些节点没有邻接点,导致有些节点会出现没有被访问到的情况
优化:初始化所有节点的是否被访问数组值都为false,然后找遍历整个数组,查找未被访问的节点进行广度优先遍历
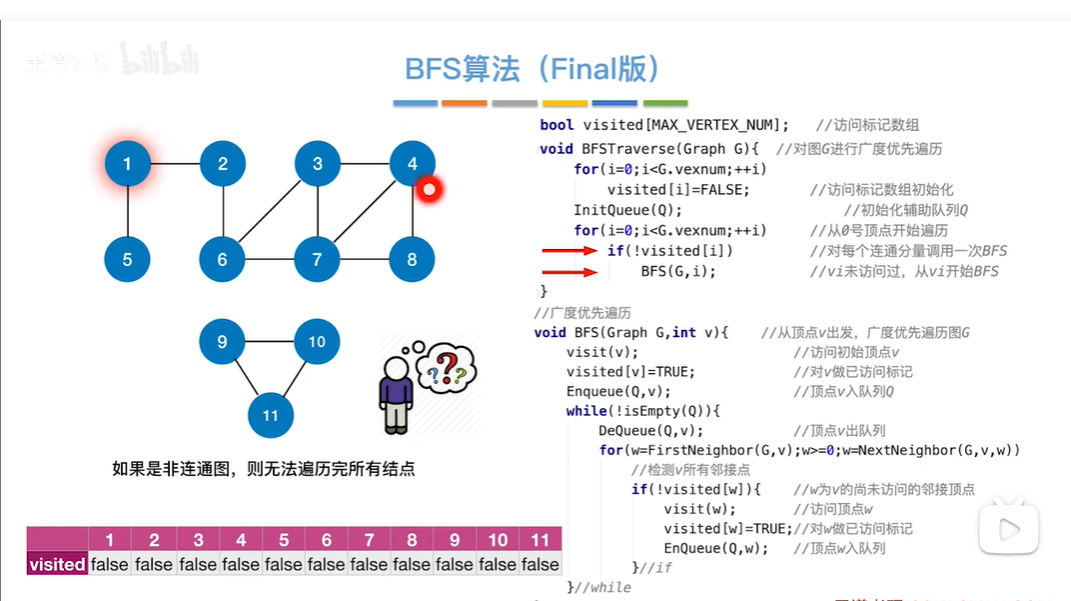
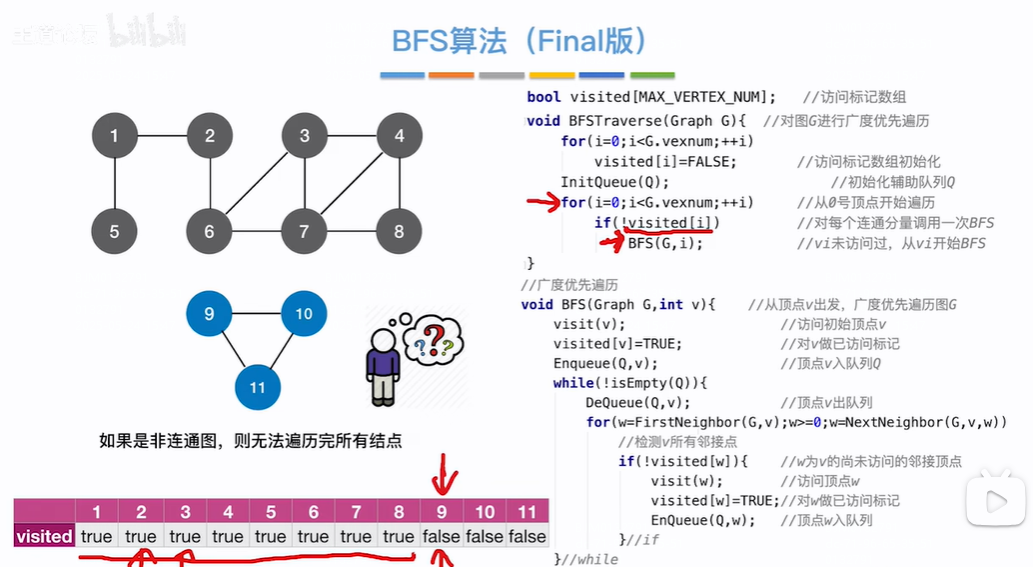
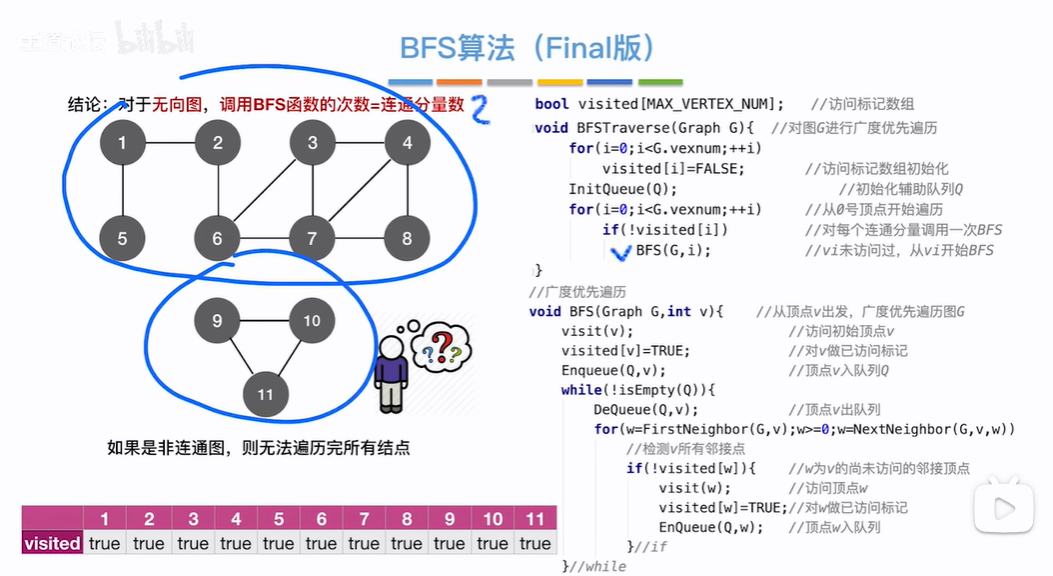
复杂度分析
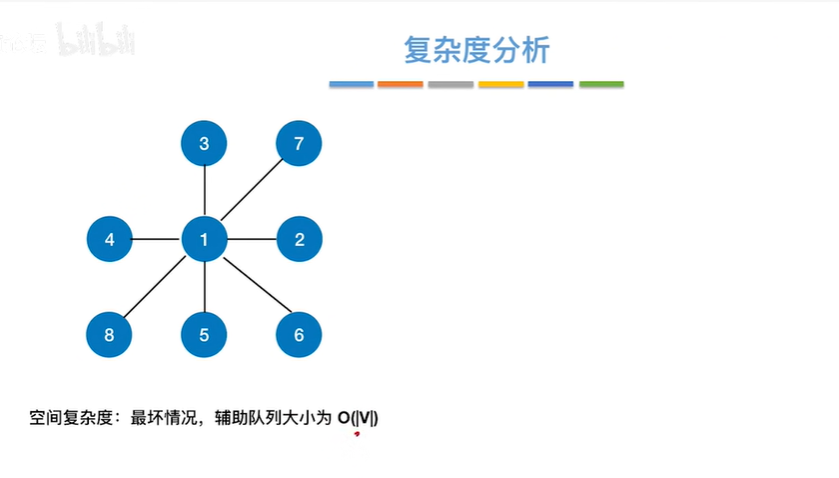
空间复杂度:
辅助队列长度的最坏情况是,某个顶点和剩余所有的顶点相邻,即在第一次访问该顶点时要把剩余所有的未被访问的顶点放到辅助队列,即最坏的情况是队列长度为顶点个数(不是顶点个数-1吗??为啥只找队列占用空间大小呢,因为队列的字段长度比数组占用空间大吗)
时间复杂度:
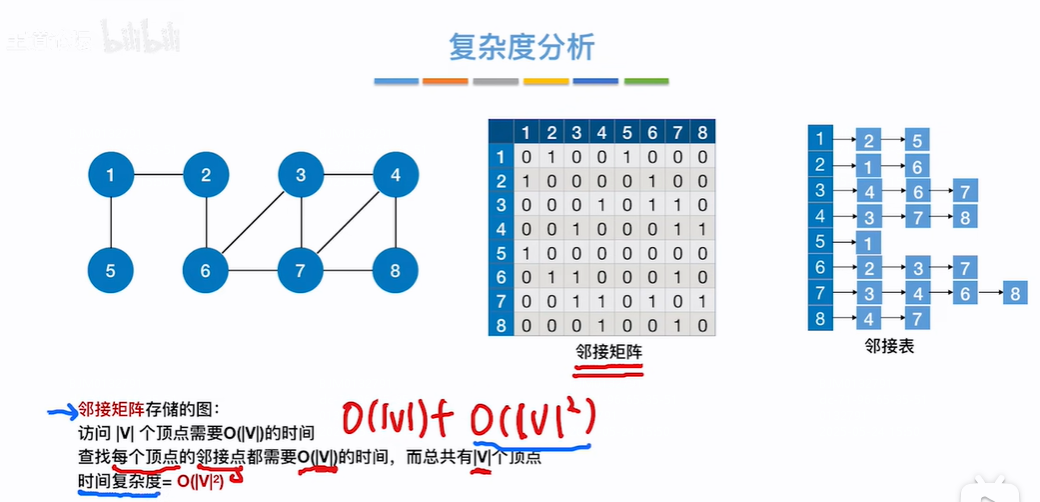
在分析图的广度优先遍历复杂度时,不要看for循环,要看访问顶点+边的时间复杂度,因为根据算法,是先访问所有顶点+各顶点邻接的边,所以看开销要看访问顶点+边几次,即有v个顶点,这v个顶点都不相邻,即没有走广度优先遍历的深层for循环,但是还是要访问一遍节点即时间复杂为O(v)(为啥不是O(1)??)
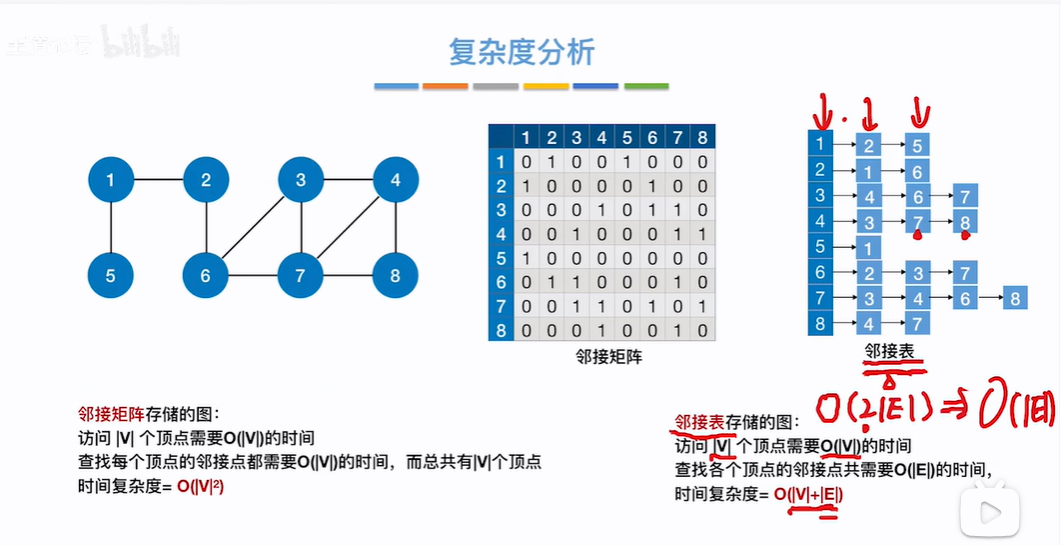
如果是邻接矩阵形式,根据算法要访问每个顶点,但还要访问每个顶点相邻的边,邻接矩阵的行和列数量都为顶点数,是否有边根据行和列决定的值即要把行列的顶点*顶点都访问一遍,即O(v*v)=O(v²)【好像是邻接矩阵的时间复杂度跟边无关】
如果是邻接表形式,根据算法要访问每个顶点O(v),但还要访问每个顶点相邻的边,每个顶点都有连线表示顶点下邻接了多少边,即为O(E),但在无向图中一条边要被访问2次,即为O(2E),即O(v)+O(2E)=O(v)+O(E)(纯属瞎写。。。。。。)
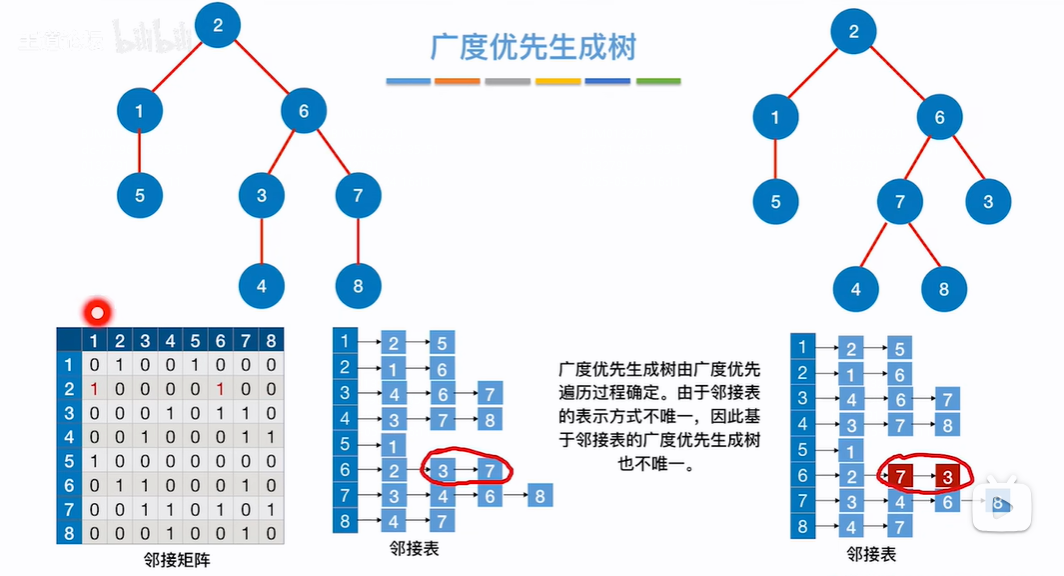
广度优先生成树:
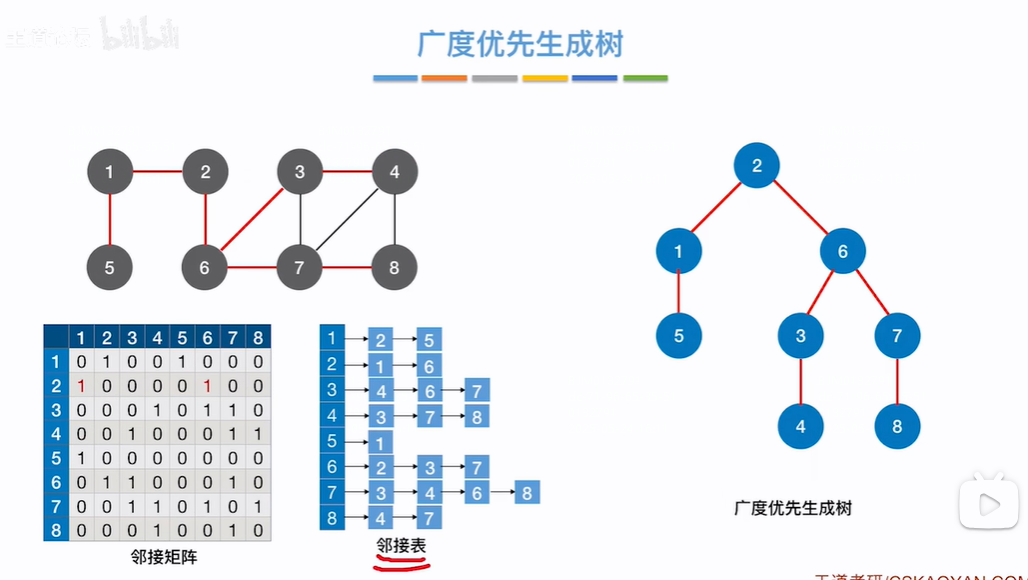
使用BFS算法,每个顶点首先被访问是从哪条边开始的,把这些边标红剩余的顶点和边连接的就是广度优先生成树
因为邻接矩阵排布唯一(节点编号自增顺序)所以广度优先生成树唯一,但是邻接表表示邻接点方式不唯一,所以邻接表方式的广度优先生成树不唯一
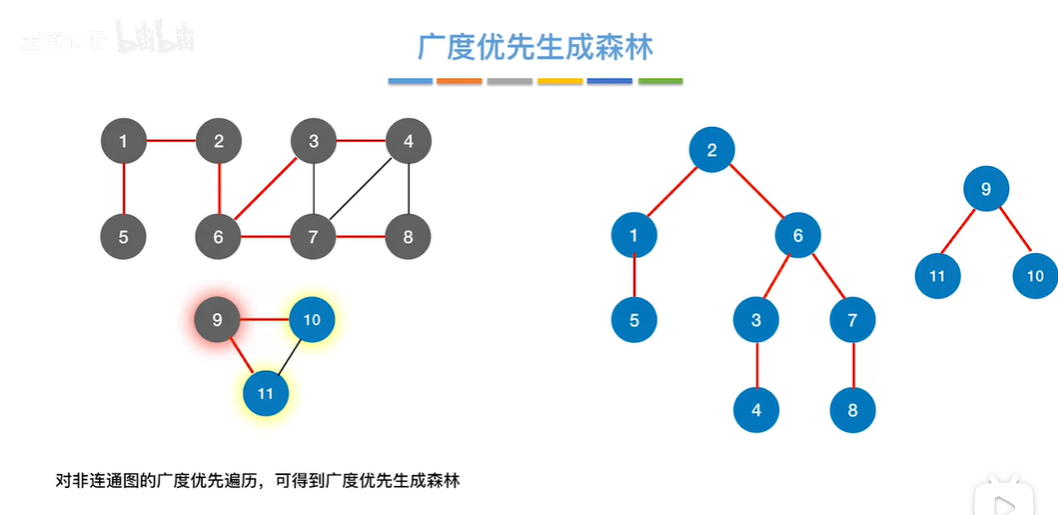
广度优先生成森林
非连通图的每个连通分量根据BFS算法广度优先遍历都有广度优先生成树,合在一起就是广度优先森林
思考:
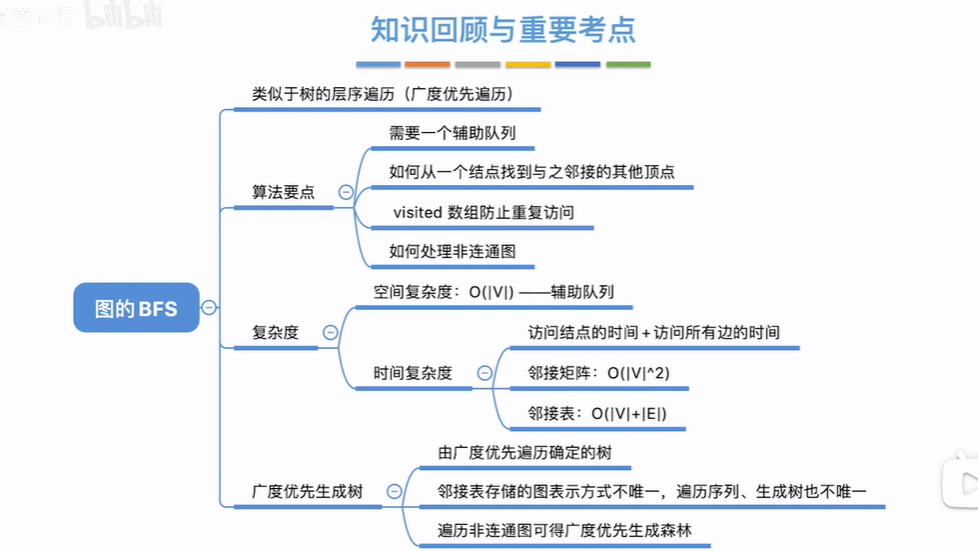
知识回顾:
请老天爷救救孩子 。。。。。。
