当前位置：首页 > ds >正文

day 12 三种启发式算法：遗传算法、粒子群算法、退火算法

ds 2025/5/5 10:58:16

启发式算法：

算法是一种机械式方法，在有限步骤内求解一个问题。最直接的解题方法是 brute-force，用暴力尝试解空间中的每个实例。但这个方法太慢了。除了brute-force以外，都可以粗略归为heuristic，企图发现和利用解空间的特有的内在结构，得到一个快速的求解算法。

启发式算法是一类用于解决复杂问题的算法策略。简单来说，它不追求找到问题的精确最优解，而是凭借经验法则、直观判断或一些试探性方法，在可接受的时间内找到一个足够好的近似解。

机器学习目标是找到一组超参数，让机器学习模型在某个指标（比如验证集准确率）上表现最好，而启发式算法就是优化器。

想象要在一个巨大的迷宫中找到出口，精确算法可能会尝试所有可能路径来确定最短路线，但这可能非常耗时。而启发式算法会根据一些线索，比如朝着离出口大致方向前进（假设能感觉到出口方向），虽然不一定是最短路径，但能较快走出迷宫。

故事背景：

为了找出地球上最高的山，一群有志的兔子们开始想办法。

一、遗传算法

灵感来源： 生物进化，达尔文的“适者生存”。

简单理解： 把不同的超参数组合想象成一群“个体”。表现好的个体（高验证分）更有机会“繁殖”（它们的参数组合会被借鉴和混合），并可能发生“变异”（参数随机小改动），产生下一代。表现差的个体逐渐被淘汰。一代代下去，种群整体就会越来越适应环境（找到更好的超参数）。

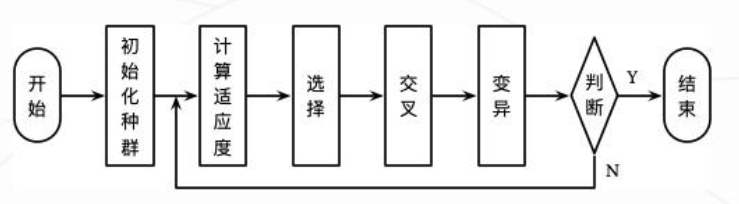
核心思想：模拟生物遗传进化过程，将问题的解编码为个体（兔子），通过选择（淘汰低海拔兔子）、交叉（优秀兔子繁衍后代，交换基因）和变异（随机因素改变基因）等操作，使种群（兔群）不断进化，朝着最优解（最高峰）方向发展。

流程：兔子们先吃了失忆药片，然后被发射到太空，之后随机降落到地球上的不同地方。起初，它们不知道自己要找最高的山这一使命。每隔几年，就把海拔低的兔子淘汰一部分，而那些处于海拔较高位置的兔子被认为是 “优秀” 的，它们有更多机会繁衍后代。经过多代繁衍，兔子们逐渐集中在高海拔区域，最终找到珠穆朗玛峰。

代码实例：

先在Anaconda Prompt中安装deap库：pip install deap -i https://pypi.tuna.tsinghua.edu.cn/simple

# 数据预处理
# 划分数据集
# 默认参数随机森林模型训练
# from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import classification_report, confusion_matrix
import warnings
warnings.filterwarnings("ignore")
import time
# deap是一个用于遗传算法和进化计算的Python库
from deap import base, creator, tools, algorithms 
import random
import numpy as npprint("\n--- 2. 遗传算法优化随机森林 (训练集 -> 测试集) ---")# 定义适应度函数和个体类型
# 适应度值就是随机森林模型在测试集上的准确率，权重1.0表示希望最大化适应度值。
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
# 每个个体代表一组随机森林的超参数组合。
creator.create("Individual", list, fitness=creator.FitnessMax)# 定义超参数范围
n_estimators_range = (50, 200)
max_depth_range = (10, 30)
min_samples_split_range = (2, 10)
min_samples_leaf_range = (1, 4)# 初始化工具盒，用于注册遗传算法中使用的各种操作。
toolbox = base.Toolbox()# 定义基因生成器，每个生成器用于在指定范围内随机生成一个超参数值
toolbox.register("attr_n_estimators", random.randint, *n_estimators_range)
toolbox.register("attr_max_depth", random.randint, *max_depth_range)
toolbox.register("attr_min_samples_split", random.randint, *min_samples_split_range)
toolbox.register("attr_min_samples_leaf", random.randint, *min_samples_leaf_range)# 定义个体生成器，通过循环调用基因生成器来初始化一个个体
toolbox.register("individual", tools.initCycle, creator.Individual,(toolbox.attr_n_estimators, toolbox.attr_max_depth,toolbox.attr_min_samples_split, toolbox.attr_min_samples_leaf), n=1)# 定义种群生成器，通过重复调用个体生成器来创建一个种群
toolbox.register("population", tools.initRepeat, list, toolbox.individual)# 定义评估函数，将个体解包为超参数，创建并训练模型，预测返回准确率作为个体的适应度值。
def evaluate(individual):n_estimators, max_depth, min_samples_split, min_samples_leaf = individualmodel = RandomForestClassifier(n_estimators=n_estimators,max_depth=max_depth,min_samples_split=min_samples_split,min_samples_leaf=min_samples_leaf,random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)return accuracy,# 注册评估函数
toolbox.register("evaluate", evaluate)# 注册遗传操作（交叉、变异和选择）
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutUniformInt, low=[n_estimators_range[0], max_depth_range[0],min_samples_split_range[0], min_samples_leaf_range[0]],up=[n_estimators_range[1], max_depth_range[1],min_samples_split_range[1], min_samples_leaf_range[1]], indpb=0.1)
toolbox.register("select", tools.selTournament, tournsize=3)# 初始化种群
pop = toolbox.population(n=20)# 遗传算法参数
NGEN = 10 # 表示遗传算法的进化代数，即算法运行的迭代次数。
CXPB = 0.5 # 交叉概率，即两个个体进行交叉操作的概率。
MUTPB = 0.2 # 变异概率，即个体的某个基因发生变异的概率。# 运行遗传算法
start_time = time.time()
for gen in range(NGEN):offspring = algorithms.varAnd(pop, toolbox, cxpb=CXPB, mutpb=MUTPB)fits = toolbox.map(toolbox.evaluate, offspring)for fit, ind in zip(fits, offspring):ind.fitness.values = fitpop = toolbox.select(offspring, k=len(pop))
end_time = time.time()# 找到最优个体并解包得到最优参数值
best_ind = tools.selBest(pop, k=1)[0]
best_n_estimators, best_max_depth, best_min_samples_split, best_min_samples_leaf = best_ind
print(f"遗传算法优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", {'n_estimators': best_n_estimators,'max_depth': best_max_depth,'min_samples_split': best_min_samples_split,'min_samples_leaf': best_min_samples_leaf
})# 使用最佳参数的模型进行预测
best_model = RandomForestClassifier(n_estimators=best_n_estimators,max_depth=best_max_depth,min_samples_split=best_min_samples_split,min_samples_leaf=best_min_samples_leaf,random_state=42)
best_model.fit(X_train, y_train)
best_pred = best_model.predict(X_test)print("\n遗传算法优化后的随机森林 在测试集上的分类报告：")
print(classification_report(y_test, best_pred))
print("遗传算法优化后的随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, best_pred))

二、粒子群算法

灵感来源： 鸟群或鱼群觅食。

简单理解： 把每个超参数组合想象成一个“粒子”（鸟）。每个粒子在参数空间中“飞行”。它会记住自己飞过的最好位置，也会参考整个“鸟群”发现的最好位置，结合这两者来调整自己的飞行方向和速度，同时带点随机性。

核心思想：每个粒子（兔子）通过跟踪自身的历史最优位置和群体的全局最优位置来调整自身的搜索方向，粒子间通过信息共享与协作，在解空间中进行高效搜索，从而找到问题的最优解，就像兔群最终找到珠穆朗玛峰一样。

和 OSPF（开放最短路径优先）广播路由算法好像有一些相似性：

粒子群算法：粒子之间通过共享全局最优位置（ gbest ）信息，每个粒子根据自身最优位置（ pbest ）和 gbest 来调整飞行方向和速度，粒子间相互协作，共同寻找最优解。并且粒子的速度和位置根据迭代过程中自身和全局信息不断动态调整，以适应搜索空间，逐步接近最优解。

OSPF 广播路由算法：路由器之间通过广播链路状态信息，每台路由器都了解网络中其他路由器的链路状态，基于这些共享信息，所有路由器共同计算出到达各个网络节点的最短路径，也存在信息共享与协作机制。当网络拓扑发生变化时，路由器会重新广播链路状态更新信息，各路由器基于新信息重新计算路由表，动态调整数据包的转发路径，以适应网络的变化。

流程：每只兔子都作为一个粒子，它们在地球上随机分布。每只兔子都知道自己当前位置的海拔高度，同时记住自己曾经到达过的最高海拔位置（个体最优位置，记为 pbest ）。所有兔子还共享整个群体到目前为止发现的最高海拔位置（全局最优位置，记为 gbest ）。在每次跳跃时，兔子会综合考虑自己的 pbest 和群体的 gbest 来调整跳跃方向和距离。例如，会按照一定比例朝着 pbest 和 gbest 的方向跳动，也会有一定的随机因素影响跳跃。经过多次跳跃，整个兔群逐渐向地球上最高的山峰聚集。

代码实例：

print("\n--- 2. 粒子群优化算法优化随机森林 (训练集 -> 测试集) ---")# 定义适应度函数，本质就是构建了一个函数实现超参数-->评估指标的映射
def fitness_function(params): 
# 通过序列解包将 params 中的值分别赋给对应的超参数变量。n_estimators, max_depth, min_samples_split, min_samples_leaf = params model = RandomForestClassifier(n_estimators=int(n_estimators),max_depth=int(max_depth),min_samples_split=int(min_samples_split),min_samples_leaf=int(min_samples_leaf),random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)return accuracy# 粒子群优化算法实现
def pso(num_particles, num_iterations, c1, c2, w, bounds): 
# pso粒子群优化算法核心函数
# num_particles：粒子的数量，即算法中用于搜索最优解的个体数量。
# num_iterations：迭代次数，算法运行的最大循环次数。
# c1：认知学习因子，用于控制粒子向自身历史最佳位置移动的程度。
# c2：社会学习因子，用于控制粒子向全局最佳位置移动的程度。
# w：惯性权重，控制粒子的惯性，影响粒子在搜索空间中的移动速度和方向。
# bounds：超参数的取值范围，是包含多个元组的列表，每个元组表示一个超参数的最小值和最大值。num_params = len(bounds) 
# 初始化粒子位置矩阵particles = np.array([[random.uniform(bounds[i][0], bounds[i][1]) for i in range(num_params)] for _ in range(num_particles)])
# 初始化粒子速度velocities = np.array([[0] * num_params for _ in range(num_particles)])
# 初始化个体最优位置和适应度personal_best = particles.copy()personal_best_fitness = np.array([fitness_function(p) for p in particles])global_best_index = np.argmax(personal_best_fitness)
# 初始化全局最优位置和适应度global_best = personal_best[global_best_index]global_best_fitness = personal_best_fitness[global_best_index]# 迭代优化for _ in range(num_iterations):
# 生成随机数矩阵r1 = np.array([[random.random() for _ in range(num_params)] for _ in range(num_particles)])r2 = np.array([[random.random() for _ in range(num_params)] for _ in range(num_particles)])
# 更新粒子速度velocities = w * velocities + c1 * r1 * (personal_best - particles) + c2 * r2 * (global_best - particles)
# 更新粒子位置particles = particles + velocities# 边界检查（超参数取值范围）for i in range(num_particles):for j in range(num_params):if particles[i][j] < bounds[j][0]:particles[i][j] = bounds[j][0]elif particles[i][j] > bounds[j][1]:particles[i][j] = bounds[j][1]# 更新个体和全局最优位置fitness_values = np.array([fitness_function(p) for p in particles])improved_indices = fitness_values > personal_best_fitnesspersonal_best[improved_indices] = particles[improved_indices]personal_best_fitness[improved_indices] = fitness_values[improved_indices]current_best_index = np.argmax(personal_best_fitness)if personal_best_fitness[current_best_index] > global_best_fitness:global_best = personal_best[current_best_index]global_best_fitness = personal_best_fitness[current_best_index]return global_best, global_best_fitness# 超参数范围
bounds = [(50, 200), (10, 30), (2, 10), (1, 4)]  # n_estimators, max_depth, min_samples_split, min_samples_leaf# 粒子群优化算法参数
num_particles = 20
num_iterations = 10
c1 = 1.5
c2 = 1.5
w = 0.5# 运行粒子群优化算法
start_time = time.time()
best_params, best_fitness = pso(num_particles, num_iterations, c1, c2, w, bounds)
end_time = time.time()
print(f"粒子群优化算法优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", {'n_estimators': int(best_params[0]),'max_depth': int(best_params[1]),'min_samples_split': int(best_params[2]),'min_samples_leaf': int(best_params[3])
})# 使用最佳参数的模型进行预测
best_model = RandomForestClassifier(n_estimators=int(best_params[0]),max_depth=int(best_params[1]),min_samples_split=int(best_params[2]),min_samples_leaf=int(best_params[3]),random_state=42)
best_model.fit(X_train, y_train)
best_pred = best_model.predict(X_test)print("\n粒子群优化算法优化后的随机森林 在测试集上的分类报告：")
print(classification_report(y_test, best_pred))
print("粒子群优化算法优化后的随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, best_pred))

三、模拟退火算法

灵感来源： 金属冶炼中的退火过程（缓慢冷却使金属达到最低能量稳定态）。

简单理解： 从一个随机的超参数组合开始。随机尝试改变一点参数。如果新组合更好，就接受它。如果新组合更差，也有一定概率接受它（尤其是在“高温”/搜索早期）。这个接受坏解的概率会随着时间（“降温”）慢慢变小。

核心思想：模拟固体退火过程，开始时以较高的随机性（类似高温下固体粒子的无序运动）探索解空间，接受较差解的概率较大，这样有助于跳出局部最优。随着 “温度” 降低（兔子逐渐清醒），算法变得更加贪婪，更倾向于朝着已发现的较优解移动，最终收敛到一个较优解，但不一定是全局最优解。

流程：一开始兔子喝醉了，处于一种随机跳跃状态，在很长一段时间内，它随机地向各个方向跳动，期间可能走向高处，也可能踏入平地。随着时间推移，兔子渐渐清醒，开始朝着它在跳跃过程中到达过的最高处的方向跳去。

代码实例：

print("\n--- 2. 模拟退火算法优化随机森林 (训练集 -> 测试集) ---")# 定义适应度函数
def fitness_function(params): n_estimators, max_depth, min_samples_split, min_samples_leaf = paramsmodel = RandomForestClassifier(n_estimators=int(n_estimators),max_depth=int(max_depth),min_samples_split=int(min_samples_split),min_samples_leaf=int(min_samples_leaf),random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)return accuracy# 模拟退火算法实现
def simulated_annealing(initial_solution, bounds, initial_temp, final_temp, alpha):
# simulated_annealing 函数是模拟退火算法的核心函数
# 初始解 initial_solution
# 超参数取值范围 bounds
# 初始温度 initial_temp
# 终止温度 final_temp 
# 温度衰减系数 alpha current_solution = initial_solutioncurrent_fitness = fitness_function(current_solution)best_solution = current_solutionbest_fitness = current_fitnesstemp = initial_temp
# 对当前解的每个超参数值进行扰动，生成邻域解while temp > final_temp:neighbor_solution = []for i in range(len(current_solution)):new_val = current_solution[i] + random.uniform(-1, 1) * (bounds[i][1] - bounds[i][0]) * 0.1new_val = max(bounds[i][0], min(bounds[i][1], new_val))neighbor_solution.append(new_val)
#接受邻域解并更新当前适应度值neighbor_fitness = fitness_function(neighbor_solution)delta_fitness = neighbor_fitness - current_fitnessif delta_fitness > 0 or random.random() < np.exp(delta_fitness / temp):current_solution = neighbor_solutioncurrent_fitness = neighbor_fitness
# 更新最优解并按温度衰竭系数进行降温if current_fitness > best_fitness:best_solution = current_solutionbest_fitness = current_fitnesstemp *= alphareturn best_solution, best_fitness# 超参数范围
bounds = [(50, 200), (10, 30), (2, 10), (1, 4)]  # n_estimators, max_depth, min_samples_split, min_samples_leaf# 模拟退火算法参数
initial_temp = 100 # 初始温度
final_temp = 0.1 # 终止温度
alpha = 0.95 # 温度衰减系数# 初始化初始解
initial_solution = [random.uniform(bounds[i][0], bounds[i][1]) for i in range(len(bounds))]# 运行模拟退火算法
start_time = time.time()
best_params, best_fitness = simulated_annealing(initial_solution, bounds, initial_temp, final_temp, alpha)
end_time = time.time()print(f"模拟退火算法优化耗时: {end_time - start_time:.4f} 秒")
print("最佳参数: ", {'n_estimators': int(best_params[0]),'max_depth': int(best_params[1]),'min_samples_split': int(best_params[2]),'min_samples_leaf': int(best_params[3])
})# 使用最佳参数的模型进行预测
best_model = RandomForestClassifier(n_estimators=int(best_params[0]),max_depth=int(best_params[1]),min_samples_split=int(best_params[2]),min_samples_leaf=int(best_params[3]),random_state=42)
best_model.fit(X_train, y_train)
best_pred = best_model.predict(X_test)print("\n模拟退火算法优化后的随机森林 在测试集上的分类报告：")
print(classification_report(y_test, best_pred))
print("模拟退火算法优化后的随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, best_pred))