一个整数n可以有多种分划，分划的整数之和为n，在不区分分划出各整数的次序时，字典序递减输出n 的各详细分划方案和分划总数，详解

目录

题目

解题思路

代码

---

题目

一个整数n(可以有多种分划，分划的整数之和为n，在不区分分划出各整数的次序时，字典序递减输出n 的各详细分划方案和分划总数。

例如n = 6，程序输出为：

6

5  1

4  2

4  1  1

3  3

3  2  1

3  1  1  1

2  2  2

2  2  1  1

2  1  1  1  1

1  1  1  1  1  1

total = 11

解题思路

想了一下，这题使用dfs解题应该是没问题的

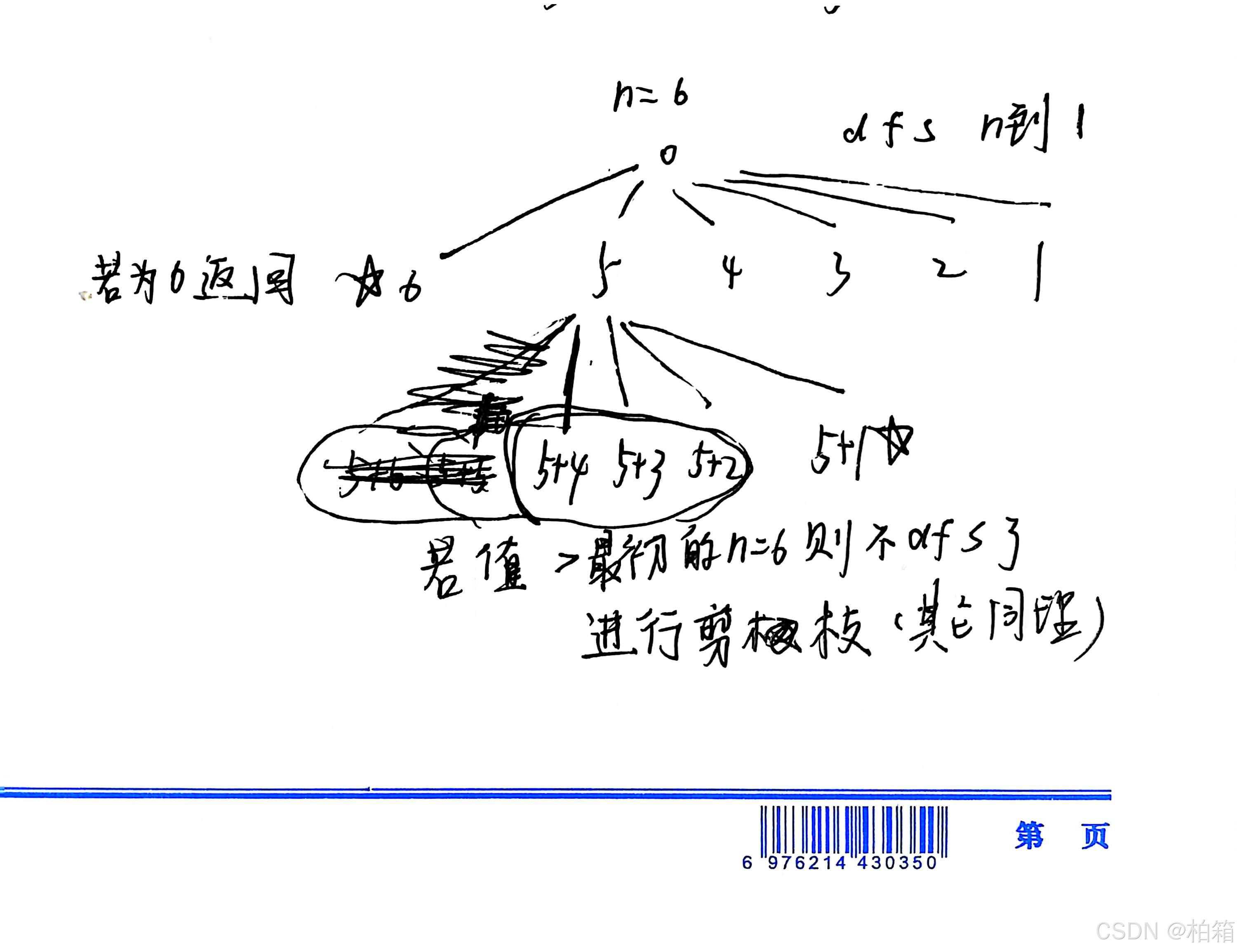
后面的思路假设n为6

设定一个sum从0开始，依次dfs6到1，让sum加上dfs的这个数，如果这个数为6，也就是n的值就可以输出这个解，并且让total加一

可以剪枝一下，如果当前的sum值大于6（n），也就不需要继续dfs了，就直接返回

最后注意题目要求字典序必须从大到小：

我解决这个问题的办法是，dfs的时候，除了传sum还要传上一个加的数字，这样在dfs的第一层，仍旧是dfs从6到1，而到之后的层就是dfs上一个加的数到1，这样就能满足题目的要求。

(*^▽^*)

下面附上我的dfs图，图中划掉了一部分是因为最开始我没看到题目要求字典序要递减(；′⌒`)

代码

#include<iostream>
#include<bits/stdc++.h>
using namespace std;int total = 0;vector<int> a;
//存一个符合条件的答案int n;void dfs(int sum,int upper) {if(sum > n) {return;//减枝}if(sum == n) {//找到符合条件的，进行输出total++;for(auto &i : a) {cout << i << ' ';}cout << '\n';return;}//因为要满足字典序递减//所以第一层遍历n到1//第二层及以后只用遍历上一层加的数到1if(upper == 0) {for(int i = n; i >= 1; i--) {sum += i;a.push_back(i);dfs(sum,i);sum -= i;a.pop_back();}}else {for(int i = upper; i >= 1; i--) {sum += i;a.push_back(i);dfs(sum,i);sum -= i;a.pop_back();}}}int main()
{cin >> n;dfs(0,0);cout << "total = " << total;return 0;
}