决策树-信息增益（第二十三节课内容总结）

决策树

从根节点开始一步步走到叶子节点（决策）， 所有的数据最终都会落到叶子节点，既可以做分类也可以做回归

熵

用于衡量数据集的不确定性或混乱程度

熵的计算公式如下：

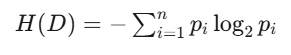
其中

H(D) 是数据集 D 的熵

pi​ 是数据集中第 i 类样本所占的比例

n 是数据集中类别的总数

熵的值越高，表示数据集的不确定性越大

信息增益

通过选择某个属性来分割数据集

其中：

IG(D,A) 是属性 A 对数据集 D 的信息增益

H(D) 是数据集 D 的熵

H(D∣A) 是在属性 A 的条件下，数据集 D 的条件熵

条件熵 H(D∣A) 的计算公式如下

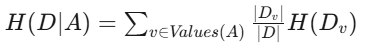
其中：

Values(A) 是属性 A 所有可能的取值。

Dv​ 是在属性 A 取值为 v 时，数据集 D 的子集。

∣Dv​∣ 是子集 Dv​ 中样本的数量。

∣D∣ 是数据集 D 中样本的总数。

计算信息增益实例：

计算信息增益:

数据集中有5个样本，其中2个属于鱼类（是），3个不属于鱼类（否）

熵的计算公式为：

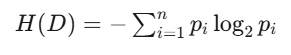
其中 pi​ 是第 i 类的概率。

对于这个数据集：

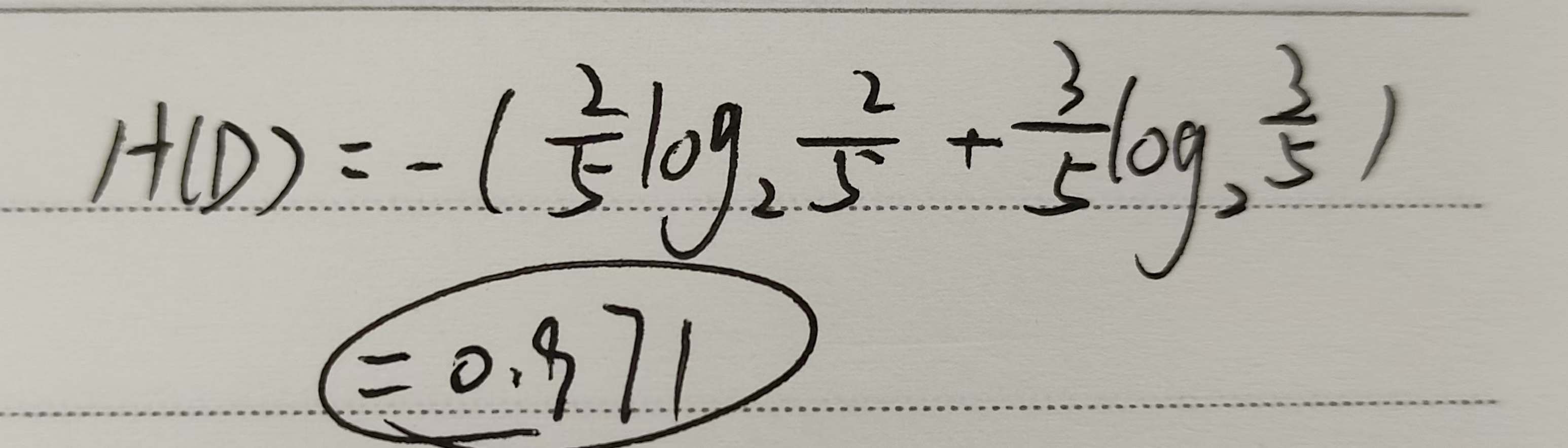
2. 计算每个属性的条件熵

属性1：不浮出水面是否可以生存

是：3个样本，其中2个是鱼类，1个不是

否：2个样本，都不是鱼类

条件熵 H(D∣A) 计算如下：

其中 H(D1​) 和 H(D2​) 分别是“是”和“否”条件下的熵。

属性2：是否有脚蹼

是：4个样本，其中2个是鱼类，2个不是

否：1个样本，不是鱼类

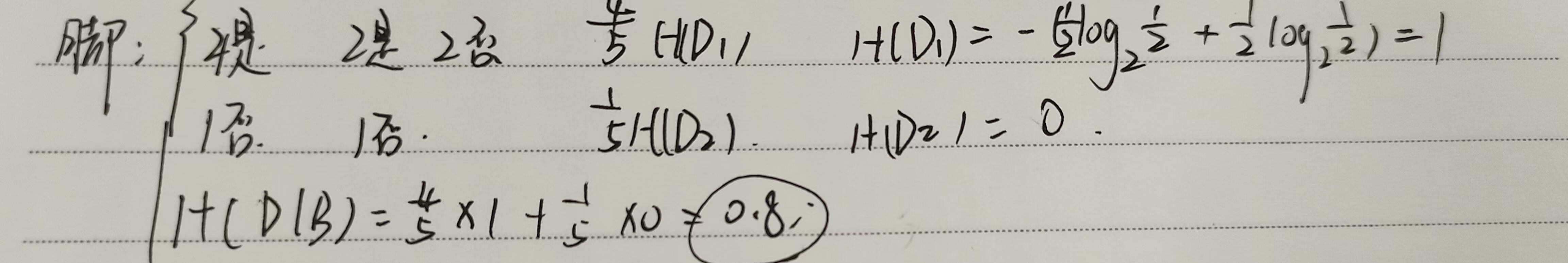
3. 计算信息增益

信息增益 IG(A) 和 IG(B) 分别为：

IG(A)=H(D)−H(D∣A)=0.971−0.551=0.420

IG(B)=H(D)−H(D∣B)=0.971−0.8=0.171

综上所述：属性“不浮出水面是否可以生存”的信息增益最大，为0.420