数据结构：严格二叉树 (Strict Binary Tree)

目录

什么是严格二叉树？(Definition)

重要术语说明

严格二叉树的高度 vs 节点数

已知高度 h，节点数 n 的范围

严格二叉树的内部节点 vs 外部节点

推导方法一：利用通用性质

推导方法二：从零开始的归纳法

---

这次我们来探讨一种特殊的、结构更规整的二叉树——严格二叉树 (Strict Binary Tree)。它的性质非常优美和确定，是很多算法（比如哈夫曼编码树）的基础。

什么是严格二叉树？(Definition)

我们从二叉树的通用定义出发进行第一性推导。

• 通用二叉树: 一个节点可以有 0 个、1 个或 2 个子节点。

• 这种定义非常灵活，但也带来不确定性。其中最“不规整”的情况就是一个节点只有1个子节点。如果我们想让树的结构更“对称”或“确定”，最直接的方法就是去掉这种中间状态。

• 推导出的新规则: 我们不允许节点有1个子节点。那么，一个节点只剩下两种可能：

  1. 它没有子节点（成为叶子节点）。

  2. 它有2个子节点。

一个严格二叉树 (Strict Binary Tree) 是指树中的每一个节点要么是叶子节点（度为0），要么拥有两个子节点（度为2）。不存在度为1的节点。

重要术语说明

这个概念在不同的书籍里有不同的叫法，很容易混淆，这里特别为你澄清：

• Strict Binary Tree (严格二叉树): 我们今天讨论的主角。

• Proper Binary Tree 或 2-tree: 也是指严格二叉树。

• Full Binary Tree: 在很多经典的英文教材（如《算法导论》）中，"Full Binary Tree" 就是指严格二叉tree。

• 但是，在国内很多教材中，"满二叉树" 指的是一种更完美的树——完美二叉树 (Perfect Binary Tree)，即所有叶子都在同一层且所有非叶子节点都有2个孩子。

• 为了避免混淆，我将统一使用“严格二叉树”这个最准确的术语。

---

严格二叉树的高度 vs 节点数

现在，我们在“严格”这个新约束下，重新审视高度和节点数的关系。

已知高度 h，节点数 n 的范围

A. 最大节点数 n_max

                ●/     \●         ●/   \     /   \●      ●  ●       ●/ \    / \ / \    / \●  ●  ●   ● ●  ●  ●   ●

第一性原理: 要想在高度为 h 的限制下容纳最多节点，我们依然要把所有位置都填满。

• 一个把所有位置都填满的树（完美二叉树），其所有内部节点的度都为2，所有叶子节点都在最底层。它天然就满足“严格二叉树”的定义。

• 因此，严格二叉树的最大节点数和普通二叉树的完全一样。

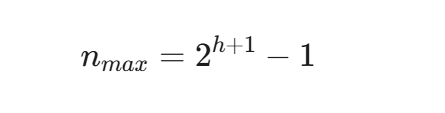
B. 最小节点数 n_min

第一性原理: 在必须达到高度 h 的前提下，使用最少的节点，并且还要遵守“要么0个孩子，要么2个孩子”的规则。

    ●/ \●   ●

    ●/ \●   ●/ \
●   ●

• 推导:

  • h=0:   只有1个根节点。它是叶子。n=1。

  • h=1:   为了达到高度1，根节点必须有孩子。根据严格定义，它不能有1个，必须有2个。这两个孩子都是叶子。所以节点数 = 1(根) + 2(孩子) = 3。

  • h=2:   为了达到高度2，我们必须在高度为1的“最瘦”严格树（3个节点）的基础上，让其中一个叶子节点“生”出孩子。

  • 我们选择一个叶子（比如左孩子），让它长出2个子节点（它们成为新的叶子）。

    • 节点数 = 1(根) + 2(第一层) + 2(第二层) = 5。

  • 发现规律: 我们发现，要让高度增加1，我们必须选择一个最深层的叶子节点，把它变成一个内部节点，并给它分配2个新的叶子节点。这个过程让总节点数增加了2。

  • 这个过程形成了一个等差数列：1, 3, 5, 7, ...

  • 其通项公式为：

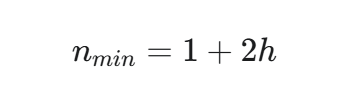
结论: 高度为 h 的严格二叉树，最少有 2h+1 个节点。

---

严格二叉树的内部节点 vs 外部节点

这是一个非常优美的性质，也是严格二叉树最重要的特性之一。

• 内部节点 (Internal Node): 非叶子节点。在严格二叉树中，就是指那些有2个子节点的节点。

• 外部节点 (External Node): 叶子节点。

我们来寻找二者数量上的关系。设 I 为内部节点数，E 为外部节点（叶子）数。

推导方法一：利用通用性质

1. 我们在之前的文章中推导过一个适用于所有二叉树的普适公式：n_0 = n_2 + 1。

   • n_0 是度为0的节点数（叶子节点）。

   • n_2 是度为2的节点数。

2. 现在我们把这个公式应用到严格二叉树的场景中：

   • 根据定义，外部节点 E 就是叶子节点，所以 E=n_0。

   • 根据定义，内部节点 I 就是那些度为2的节点，所以 I=n_2。

   • 严格二叉树中没有度为1的节点，即 n_1=0。

3. 将 E 和 I 代入通用公式 n_0=n_2+1，直接得到：E = I + 1

---

推导方法二：从零开始的归纳法

这种方法更直观，能让你“看到”这个关系是如何形成的。

1. 基础情况: 最小的非空严格二叉树是什么？是一个单独的根节点。

   • 此时，它是一个叶子节点。

   • 内部节点数 I=0。

   • 外部节点数 E=1。

   • 关系 E=I+1 成立 (1=0+1)。

2. 生长过程: 如何从一棵严格二叉树得到一棵更大的严格二叉树？

    ●(I)/   \●(E)  ●(E)

我们必须选择一个外部节点（叶子），然后给它加上两个子节点。

    ●(I)/   \●(I)  ●(E)/ \
●(E) ●(E)

这个操作会带来什么变化？

• 被选中的那个外部节点，不再是叶子了，它变成了内部节点。

  • 所以 E 的数量减 1。

  • 所以 I 的数量加 1。

• 它新长出的两个子节点，成为了新的外部节点（叶子）。

  • 所以 E 的数量再加 2。

• 我们来计算一下 E 和 I 的净变化量：

  • I 的净变化: +1。

  • E 的净变化: −1 + 2 =+ 1。

再生长一次（选择右边的叶子）：

    ●(I)/   \●(I)  ●(I)/ \   / \
●(E)●(E)●(E)●(E)

变化分析：

• I: 2 → 3（+1）

• E: 3 → 4（-1 + 2 = +1）

• N: 5 → 7（+2）

• 关系 E = I + 1 继续成立 ✅

归纳结论: 我们从一个满足 E = I + 1 的基础状态开始，每一步生长操作，都同时给 E 和 I 增加1。

这意味着，无论这棵树如何生长，它们之间的差值将永远保持不变。

• E_new = E_old + 1

• I_new = I_old + 1

• 因此，E_new − I_new = (E_old + 1) − (I_old + 1) = E_old − I_old = 1。

• 这个关系 E = I + 1 永远成立。

一个有趣的推论:

树的总节点数 N = I + E。 将 E = I + 1 代入，得 N = I + ( I + 1) = 2I + 1 。 这意味着，任何非空严格二叉树的总节点数永远是奇数。