系统学习算法:专题十六 字符串
题目一:
 算法原理:
算法原理:
其实这道其实就是偏模拟的题,即比较所有字符串,找出相同的字符,最后就是最长公共前缀
其中有两种方法,一种是两两比较,还有一种是统一比较
方法一:两两比较
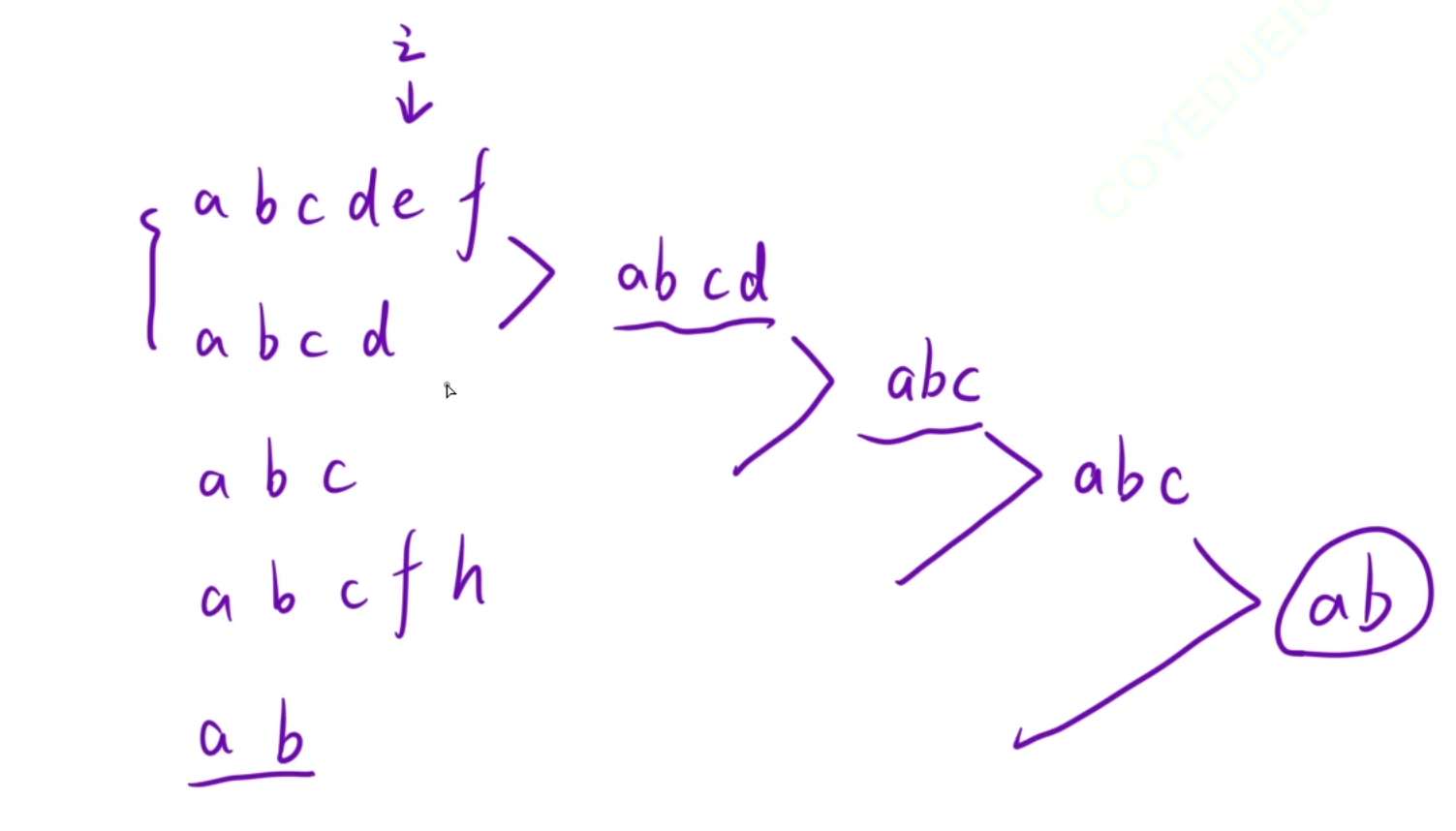
如上图,两两比较,最后一组比较完就是最长公共前缀
时间复杂度是O(mn),m是字符串长度,n是字符串个数
方法二:统一比较

即按照字符串从前往后的顺序,遍历字符,看看该位置的字符是否所有字符串都一样,如果不一样或者有字符串越界了,那么就停止并返回当前位置之前的所有字符,也就是最长公共前缀
代码一(两两比较):
class Solution {public String longestCommonPrefix(String[] strs) {//以第一个字符串作为比较基准String s=strs[0];//两两比较所有字符串for(int i=1;i<strs.length;i++){//更新当前最长公共前缀s=findCommon(s,strs[i]);}//返回最长公共前缀return s;}public String findCommon(String s1,String s2){//最小长度int minLen=Math.min(s1.length(),s2.length());int i=0;//如果没越界且该位置字符相同while(i<minLen&&s1.charAt(i)==s2.charAt(i)){i++;}//返回这两个字符串的最长公共前缀return s1.substring(0,i);}
}方法二(统一比较):
class Solution {public String longestCommonPrefix(String[] strs) {//以第一个字符串作为基准for(int i=0;i<strs[0].length();i++){//第一个字符串的i位置字符串char ch=strs[0].charAt(i);//统一与其他字符串进行比较for(int j=1;j<strs.length;j++){//如果出现越界或者不相等if(i==strs[j].length()||ch!=strs[j].charAt(i)){//返回最长公共前缀return strs[0].substring(0,i);}}}//说明第一个字符串本身就是最长公共前缀return strs[0];}
}题目二:
算法原理:
一开始还是暴力解法,那就是枚举出所有的子串,然后判断一下是否是最长回文子串,所以时间复杂度为枚举出所有子串为O(N^2),判断一下是否是最长回文子串O(N),所以综上时间复杂度为O(N^3)
这里采用中心扩展算法,刚好利用了回文字符串的特性,即以当前位置为中心,向左右扩展,此时就可以判断是否为回文字符串,如果不为回文字符串了,就看看需不需要更新结果
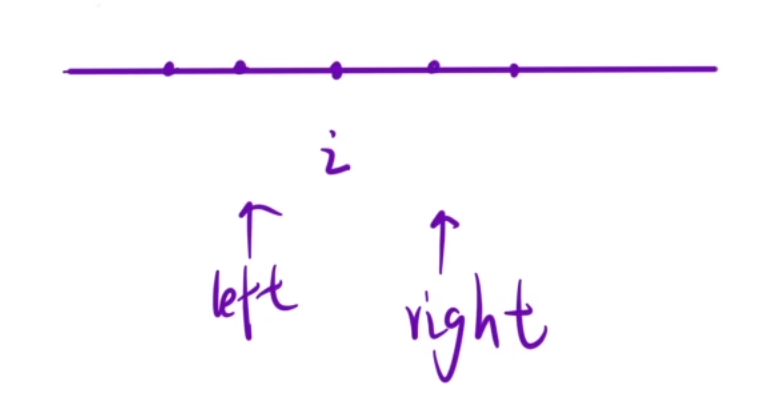
细节就是奇数和偶数长度的回文字符串,左右扩展的起始位置不一样
奇数情况很好想
偶数情况也不难想
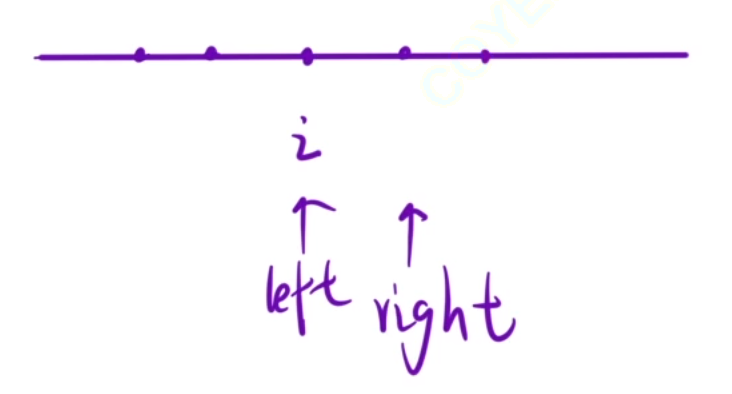
因此需要判断两次,第一次判断以当前位置为中心的奇数长度的回文串,第二次判断以当前位置为中心的偶数长度的回文串
剩下的判断回文串的操作那就很简单了,两两比较,然后移动指针,直到有一方越界
代码:
class Solution {public String longestPalindrome(String s) {//最长回文子串的长度int maxLen=0;//最长回文String ret=new String();//遍历字符串确定中心点for(int i=0;i<s.length();i++){//奇数情况int left=i-1;int right=i+1;while(left>=0&&right<s.length()){if(s.charAt(left)==s.charAt(right)){left--;right++;}else{break;}}if(right-left-1>maxLen){maxLen=right-left-1;ret=s.substring(left+1,right);}//偶数情况left=i;right=i+1;while(left>=0&&right<s.length()){if(s.charAt(left)==s.charAt(right)){left--;right++;}else{break;}}if(right-left-1>maxLen){maxLen=right-left-1;ret=s.substring(left+1,right);}}return ret;}
}题目三:
算法原理:
其实就是模拟加法,运算方法就是列竖式运算
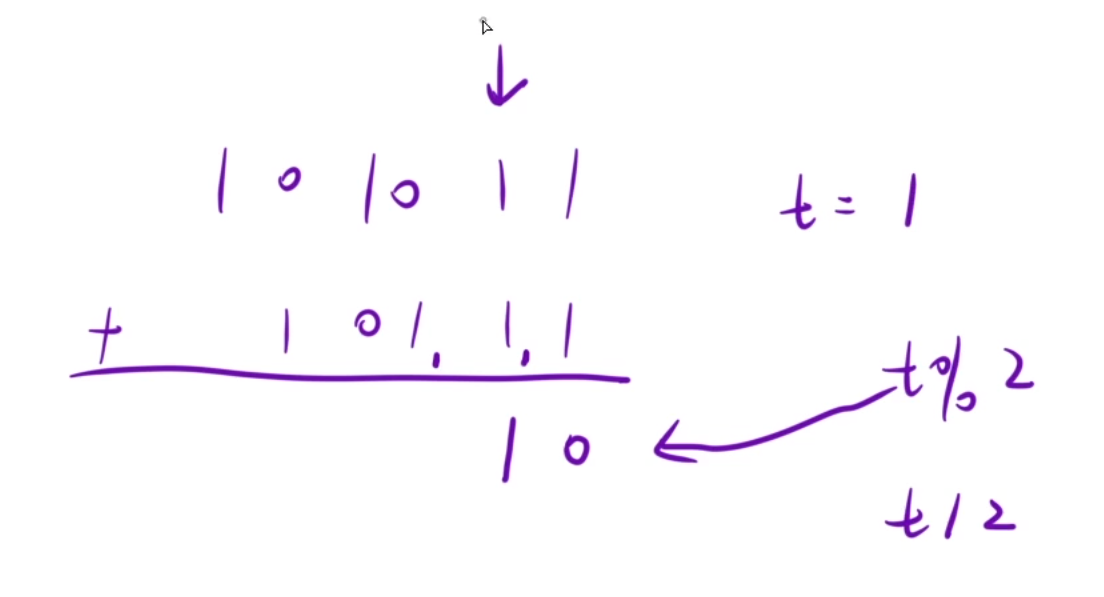
用一个变量t表示两数之和,两数相加后,根据进制来决定除和模的多少,比如二进制, 那么进完位后,剩下的值就是t%2,要进的位就是t/2
如果出现某一位一个有数,一个没数,那么默认没数的为0计算就行
然后这道题又是字符串形式,所以需要采用一些字符串转整数等一系列方法
需要注意的是,计算过程是先算低位再算高位,对应的字符串上,字符串后面的是低位,前面的是高位,所以要从字符串后面往前面遍历
代码:
class Solution {public String addBinary(String a, String b) {//从后往前遍历int cur1=a.length()-1,cur2=b.length()-1;//某一位的两数之和int t=0;//结果StringBuffer ret=new StringBuffer();//当某一个数还没计算完,或者还有进位没有用上while(cur1>=0||cur2>=0||t!=0){//加上aif(cur1>=0){t+=a.charAt(cur1)-'0';cur1--;}//加上bif(cur2>=0){t+=b.charAt(cur2)-'0';cur2--;}//头插ret.insert(0,String.valueOf(t%2));//进位t/=2;}//返回return ret.toString();}
}题目四:

算法原理:
第一种方法那就是模拟乘法运算,用列竖式去运算两数乘法

思路很简单,就是代码写起来比较复杂,第一步就是固定其中一个字符串的一个数,然后去遍历另一个字符串的所有数挨个去乘,得到一个数
但是在这里需要注意,比如上图615可不是真的就615,而是6150,492也是49200,要进行补零的,解决办法就是将两数的字符串逆序,这样下标就反过来了
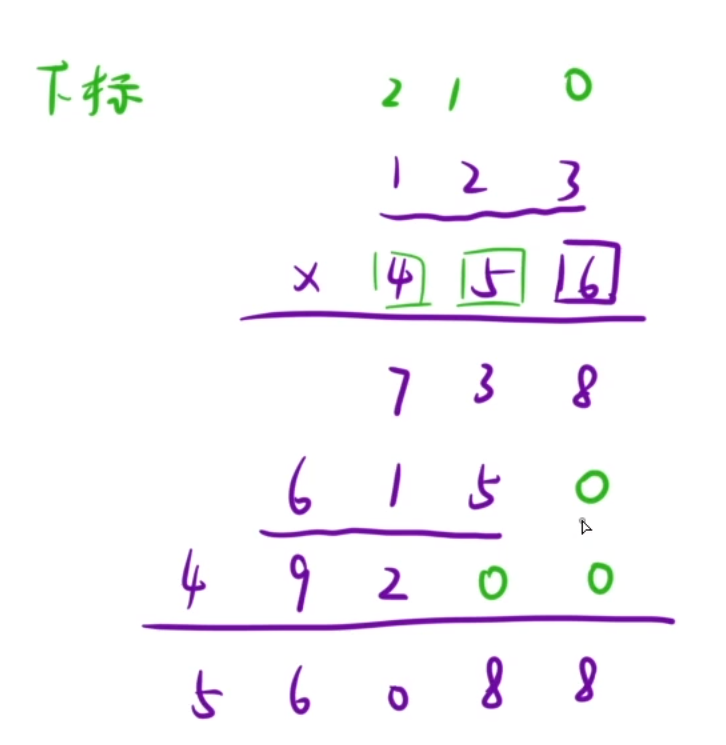
这时6在下标为0的位置,所以6乘完得到的738要补0个零
5在下标为1的位置,所以5乘完得到的615要补1个零
4在下标为2的位置,所以4乘完得到的492要补2个零
最后再将得到的这些数又进行相加的操作
相加完还要处理一下前导零的情况,总之细节很多,难度比较大
解法二:
是对解法一的优化,解法一是每算完一步都进位,也就是我们现实用的方法
解法二是无进位相乘然后相加,最后处理进位

然后还需要知道的是,m位数*n位数=(m+n-1)位数
因此我们就可以用int数组来接收每一位的未进位的数,至于如何一一对应存放顺序,则还是先将两个字符串逆序,将下标反过来
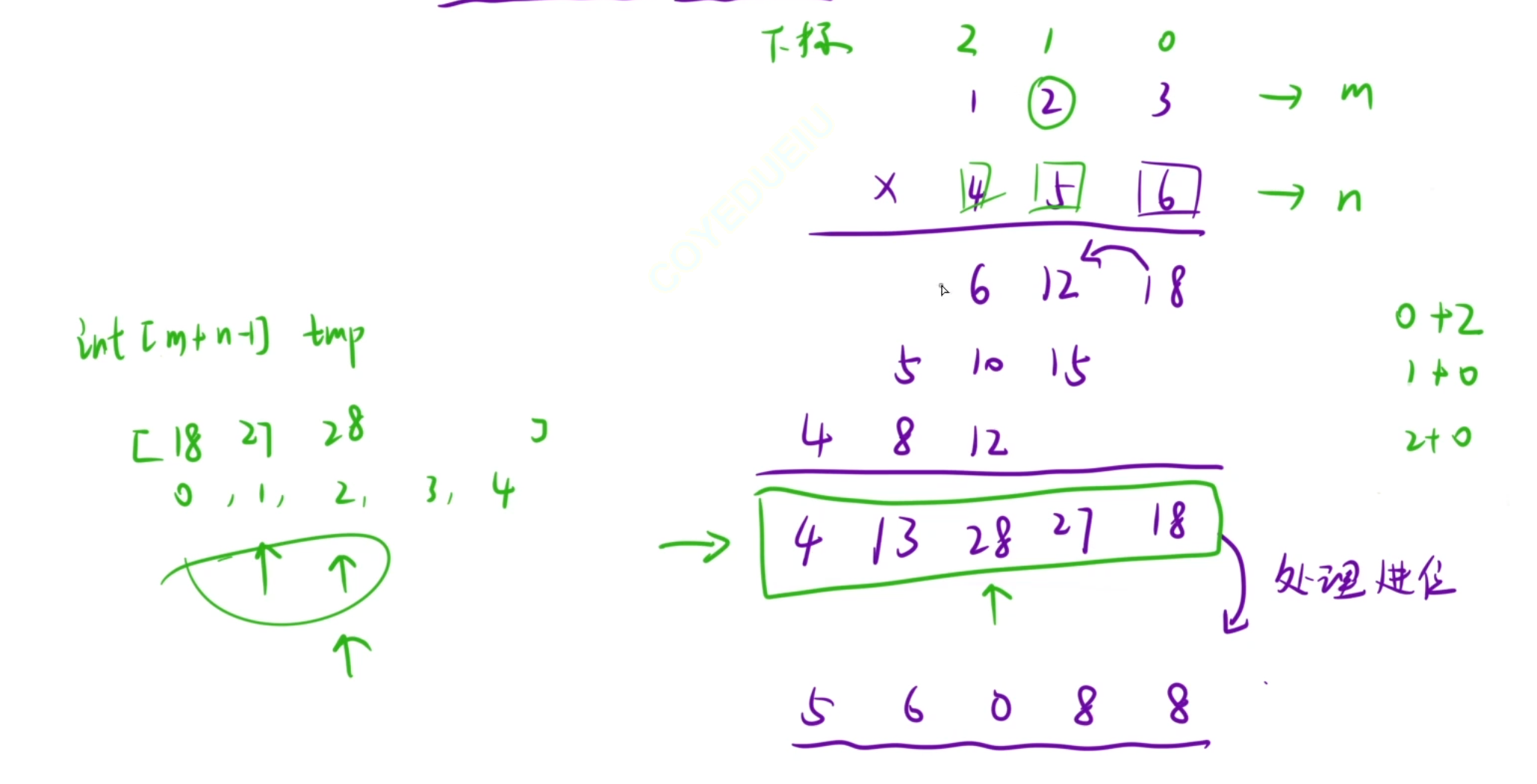
则6*3=18时,3在下标0位,6在下标0位,0+0=0,所以18放在数组下标0位
6*2=12时,2在下标1位,6在下标0位,1+0=0,所以12放在数组下标1位
6*1=6时,1在下标2位,6在下标0位,2+0=0,所以6放在数组下标2位
如此类推,全部加到数组后,数组里存的就是:4 13 28 27 18
然后再处理进位,那就模拟与0相加即可
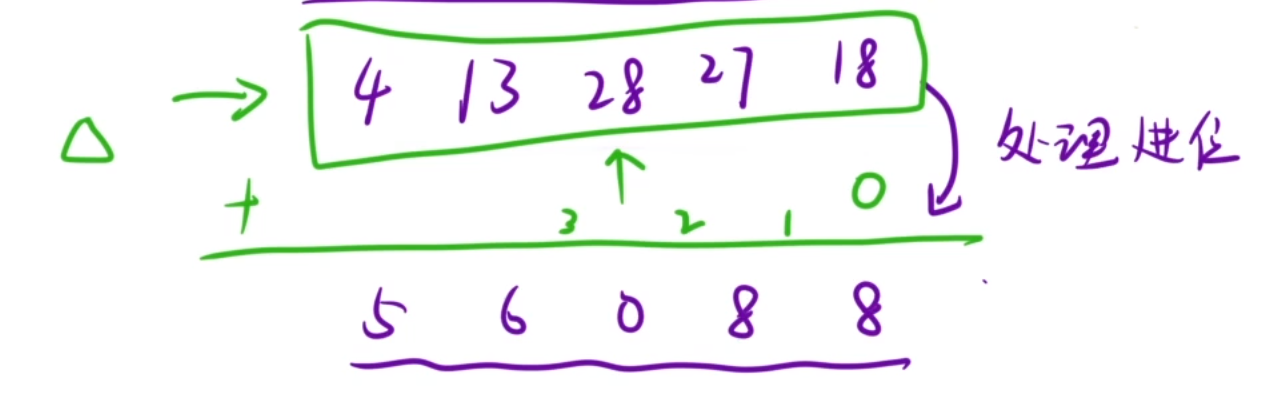
最后再处理一下前导零的问题
思路基本是想不出来的,就看知不知道了,知道这种思路的话,那代码就很好写了
解法二这种就属于思路难,代码简单,解法一则是思路简单,代码难
代码(解法二):
class Solution {public String multiply(String num1, String num2) {//初始化,将两个字符串翻转int l1=num1.length(),l2=num2.length();char[] n1=new StringBuffer(num1).reverse().toString().toCharArray();char[] n2=new StringBuffer(num2).reverse().toString().toCharArray();//m位数*n位数=(m+n-1)位数int[] tmp=new int[l1+l2-1];//固定其中一个字符串的一个数,与另一个字符串的所有数相乘,放在数组i+j位上for(int i=0;i<l1;i++){for(int j=0;j<l2;j++){tmp[i+j]+=(n1[i]-'0')*(n2[j]-'0');}}//加法进位int cur=0,t=0;StringBuffer ret=new StringBuffer();while(cur<tmp.length||t!=0){if(cur<tmp.length){t+=tmp[cur];cur++;}ret.insert(0,String.valueOf(t%10));t/=10; }//处理前导零问题cur=0;while(ret.length()>1&&ret.charAt(cur)=='0'){ret.deleteCharAt(cur);}//返回return ret.toString();}
}总结:
字符串的题也基本就是模拟以及各种算法的杂糅,主要要掌握一些常见的Java自带的字符串封装好的方法
