一致连续性背后的直觉是什么?
Uniform continuity
一、说明
在计算机作图或工程运算,并不需要在【-∞,∞】上考虑问题。能在一个区间保证处处可微就足以。因此引出一致连续性问题。本篇就谈谈啥叫一致连续函数。
二、概念和定义
2.1 简单连续
简单连续性是其最弱的形式。它告诉我们,如果我们想知道目标函数的值f在一定容忍范围内ϵ达到目标值x,但使用近似值x′精度有限,而不是真实值x我们可能无法获得或以其他方式知道无限的精度,即我们想要
∣f(x1)−f(x2)∣<ϵ| f(x_1 )−f(x_2) | < ϵ∣f(x1)−f(x2)∣<ϵ
那么我们就能得到这个,如果我们可以测量x足够准确,也就是说,我们可以
∣x1−x2∣<δ| x_1−x_2| <δ∣x1−x2∣<δ
对于一些δ> 0
这可能对每个x来说都一样,也可能不一样ϵ和x.
【1】简单连续例
对于函数y=x2y=x^2y=x2,在x∈[−∞,∞]x\in[-\infin,\infin]x∈[−∞,∞]是连续的,
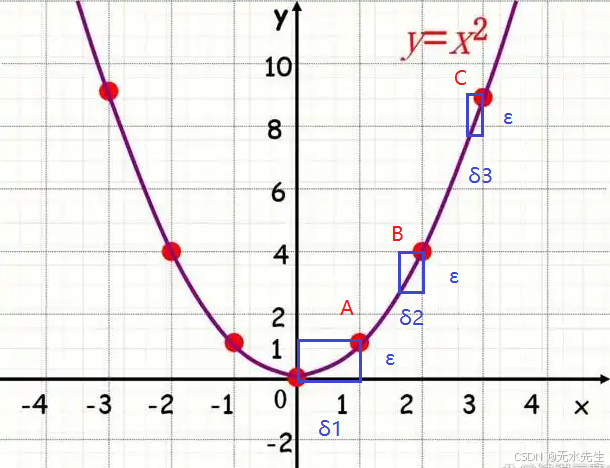
在A,B,C三个点附近,给出一个条件:
∣f(x1)−f(x2)∣<ϵ| f(x_1 )−f(x_2) | < ϵ∣f(x1)−f(x2)∣<ϵ
显然,对应的有Δx<δ1\Delta{x}<\delta 1Δx<δ1,Δx<δ2\Delta{x}<\delta 2Δx<δ2,Δx<δ3\Delta{x}<\delta 3Δx<δ3能满足上面等式。然而:
δ1>δ2>δ3>....\delta 1>\delta 2>\delta 3>....δ1>δ2>δ3>....
- 即每个点附近,δi\delta iδi是不一致的。
- 随着x在正半轴的递增延续,对应ε的δi递减,接近0。
【2】另一个例子
依然是对于函数y=x2y=x^2y=x2,在x∈[−3,3]x\in[-3,3]x∈[−3,3]是连续的,
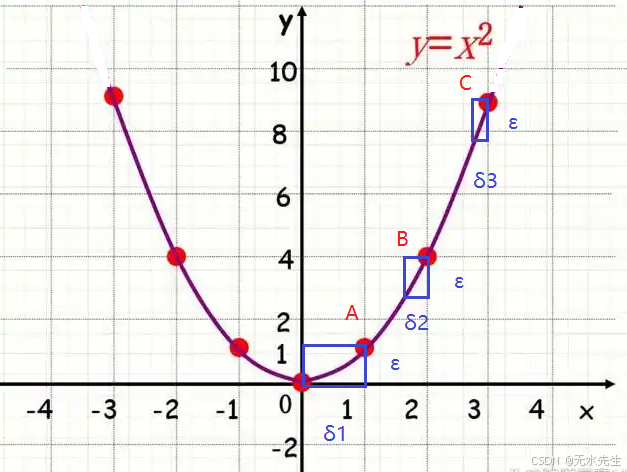
但是,在A,B,C三个点附近,给出一个条件:
∣f(x1)−f(x2)∣<ϵ| f(x_1 )−f(x_2) | < ϵ∣f(x1)−f(x2)∣<ϵ
显然,对应的有Δx<δ1\Delta{x}<\delta 1Δx<δ1,Δx<δ2\Delta{x}<\delta 2Δx<δ2,Δx<δ3\Delta{x}<\delta 3Δx<δ3能满足上面等式。然而:
δ1>δ2>δ3\delta 1>\delta 2>\delta 3δ1>δ2>δ3
- 即每个点附近,只要将δi\delta iδi替换成δ3\delta 3δ3就能保证定义域内部任意一点处有:
∣f(x1)−f(x2)∣<ϵ| f(x_1 )−f(x_2) | < ϵ∣f(x1)−f(x2)∣<ϵ
所以说,函数y=x2y=x^2y=x2在一个闭区间内是一致连续的。
2.2 一致连续
一致连续性是函数的一种性质,其中函数值的接近程度仅取决于其输入的接近程度,而不取决于它们在域内的具体位置 简而言之,如果能找到一个适用于整个域的“接近度”值(delta),确保输s入中彼此接近的点在输出中也彼此接近,则该函数是一致连续的。 这与常规连续性不同,常规连续性的“接近度”值(delta)可能会根据域中的特定点而变化。
以下是更正式的解释:
定义:函数 f:D−>Rf:D -> Rf:D−>R(其中 D 是实数子集)在 D 上一致连续,如果对于每个ε>0ε > 0ε>0,都存在一个 δ>0δ > 0δ>0,使得对于 D 中的所有 x、y,如果 ∣x−y∣<δ|x - y| < δ∣x−y∣<δ,则 ∣f(x)−f(y)∣<ε|f(x) - f(y)| < ε∣f(x)−f(y)∣<ε。
- ε :表示函数值期望的接近程度。 您希望 f(x) 和 f(y) 之间的差小于 ε。
- δ :表示输入值(x 和 y)所需的接近度。 您需要找到一个 δ,使得如果 x 和 y 彼此在 δ 范围内,则它们的函数值也将彼此在 ε 范围内。
- 均匀性:关键的区别在于,对于一致连续性,δ 必须适用于域 D 中的所有 x 和 y。在常规连续性中,δ 可能取决于您正在查看的特定点。
- 直觉:想象一下一个函数的图像。 如果一个函数是一致连续的,你可以找到一个单一的“窗口”大小(增量),当沿着图像移动时,图像始终保持在窗口的边界内。 如果函数不是一致连续的,你可能需要随着图像移动,窗口越来越小,以使图像保持在窗口的边界内。
2.3 举几个例子
1)函数 f(x)=1/(1+x2)f(x) = 1 /(1+x^2)f(x)=1/(1+x2) 在实数范围 R上.一致连续
证明:
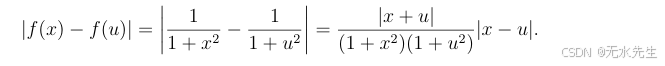
而且
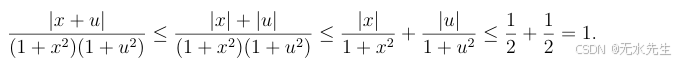
说明一个问题:
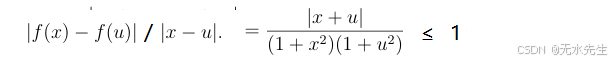 只要
只要
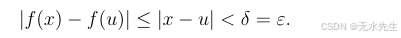
δ=ε 就能保证每一个点处都可以连续。因此是一致连续。
2)直线是一致连续的
- Lipschitz函数是一致连续的,比如:y=x2+5y=\sqrt{x^2+5}y=x2+5是一致连续的。
关于Lipschitz函数将在下一篇中讨论。
三、测量应用基础
连续性(无论其形式如何)的真正“要点”在于,它是“使计算器和测量变得有用的属性”。计算器和测量本质上是近似设备,其精度有限。因此,像计算器按钮上的那些特殊功能,如果要发挥作用,就应该具备某种“承诺”,即即使我们只知道有限精度的输入,我们至少也能知道某种有用精度的输出。
。
