当前位置：首页 > ds >正文

【计算机组成原理】原码、补码和移码

ds 2025/7/21 7:12:23

原码

表示方法

表示范围与特殊值

补码

为什么引入补码

表示方法

表示范围与特殊值

移码

表示方法

表示范围与特殊值

三码辨析：各自的优点、缺点与适用场景

各种码之间的转换与快速变换技巧

原码补码互转

补码移码互转

原码移码互转

A的补码转为﹣A的补码

在计算机中，真值是数值本身的真实含义，而机器数是用于计算机内部存储和运算的编码方式。由于计算机只能处理0和1，表示带符号数就变得复杂。为此，引入了原码（直接用最高位表示正负）、补码（将减法转化为加法、便于硬件实现统一运算）、移码（用于浮点数表示，方便比较大小）。这些编码方式是为了让计算机更高效、统一地处理正负数、整数和浮点数。

原码

表示方法

原码用机器数的最高位表示数的符号，后面的位数表示数的绝对值。

例如，A=+1110，B=-1110,字长为8位,则其原码表示为A=0,0001110,B=1,0001110,其中最高位是符号位。

表示范围与特殊值

如果用一个圆表示8位原码能够表示的所有值，其结构示意如下：

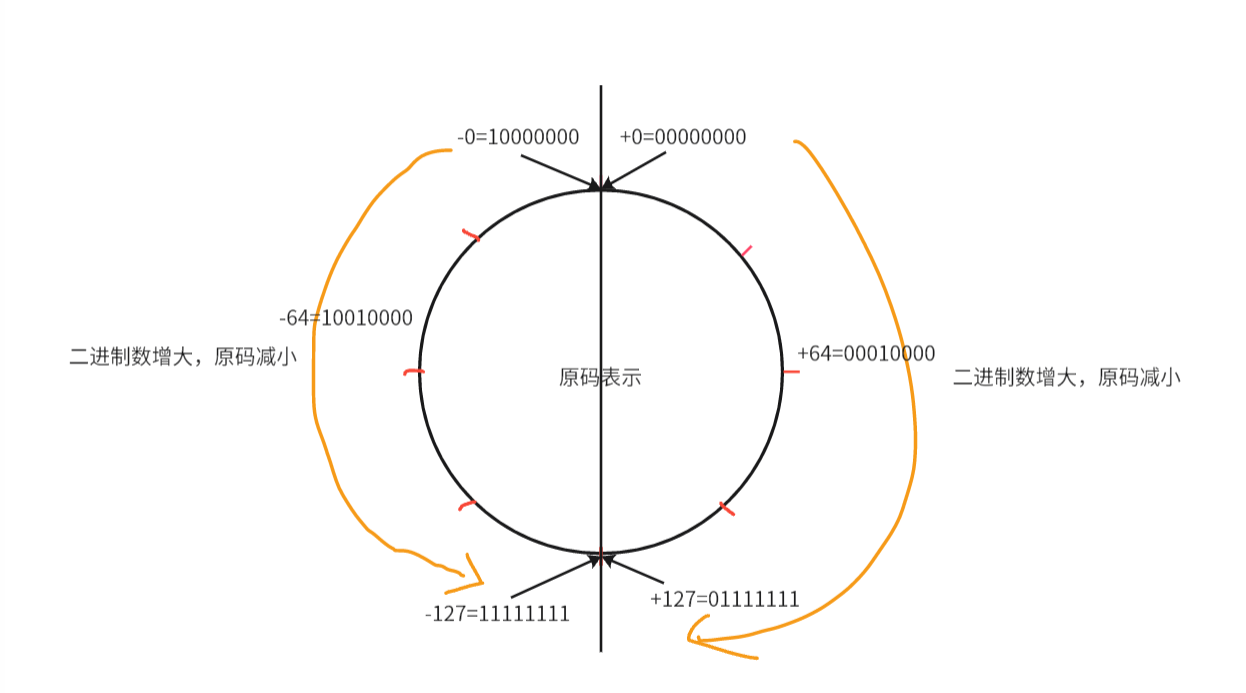
上面的图有几个特点：

1、能够表示的值最小为11111111，为-127， $2^{7}-1$ 即 $-(2^{7}-1)$ ;最大值为01111111，为+127，即 $2^{7}-1$

2、总共有两个0，分为+0与-0.

3、在圆的左半边，随着二进制数增大，原码的真值在减小；而在圆的右半边，随着二进制数增大，原码的真值在增大。也就是说原码无法构成一个时钟一样的环结构，这也是后面需要引入补码的原因。

若机器位长为n,原码的表示范围为 $[-(2^{n-1}-1),2^{n-1}-1]$ 。

原码特殊值需要记忆的是：

+0=00000000 -0=10000000 MAX=127=01111111 MIN=-127=11111111

补码

为什么引入补码

首先我们需要知道一个前置条件，在计算机的运算器中，一般来说硬件越简单越好，这样可以节省成本并且提高效率。比如说计算机需要进行加减乘除运算，但是只用一个硬件加法器和用多个硬件加法器减法器乘法器除法器，显然前者成本更低，占的空间更小。所以假如我们可以通过某种方式，使得减法能够用加法器运算，那就很好。

那么如何实现这种效果呢？这里需要引入模运算的概念。模运算中,一个数与它除以“模”后得到的余数是等价的。如：

若A、B、M满足A=B+K×M(K 为整数),记为A=B(modM),即A、B各除M以后的余数相同。

在模运算中,(A)-(B)=(A)+M-(B)(Mod M)，又M-(B)=(-B)，故可以把(A)-(B)变为A+(-B)。
补码就是为了表达“负数”在模意义下的等价形式。例如，在8位二进制中，模是 2^8=256，一个负数(-B)的补码真值就应该是 256−B，这样就可以用加法实现减法。在机器数实际操作中，若B的补码要变为-B的补码是非常好实现的（只需要把所有位按位取反再+1，这是后话），所以只需要对原码进行一些改动，使其符合模运算的规则，就能够实现减法变加法的操作。

而模运算实际上和环结构是等价的（转完一圈后归零），所以只需要思考怎么把机器数和真值搞成一个环即可。

同样还是一个圆结构，观察如何更改数字能够让其变为一个环，即随着二进制数沿着顺时针或者逆时针方向增大，机器码也能够与其一同正向变换。且看下图：

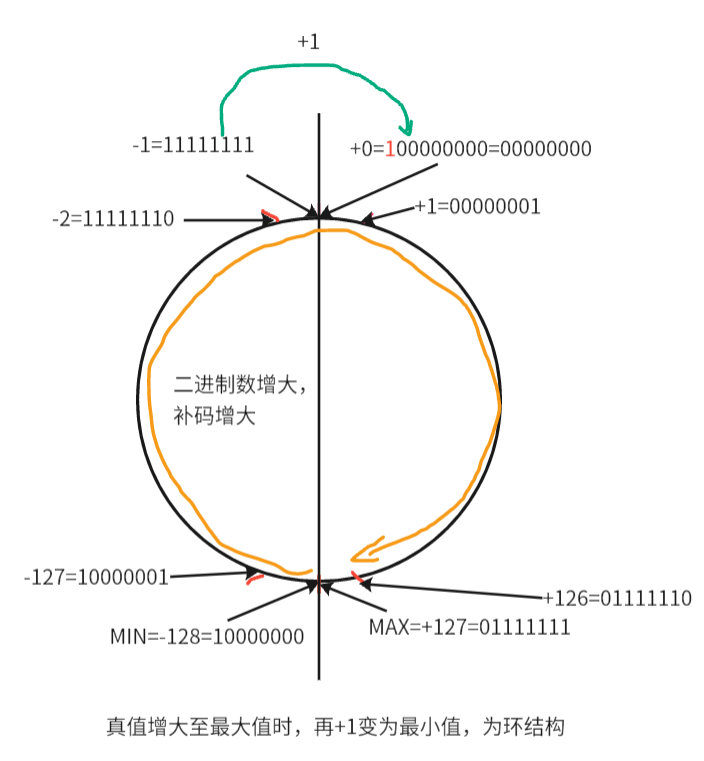
上面的圆对原码表示方法做了一些改动，使得这种机器码的表达方式（补码）能够使得其像一个时钟一样成为一个环结构。其特点如下：

1、当补码的真值增加到最大，机器码再+1变为10000000，使其对应最小值-128，而非原码的-0，实现首尾相接。

2、当补码在左半边时，机器码每+1（为了与右半边协同，顺时针方向行动视为+1），真值也需要+1。于是规定：当补码为负数时，其值为原码的除符号位所有值按位取反后再+1。这样的变换规则也符合模运算的数学定义。

3、当补码的机器码增加到最大，即11111111，此时按照2的规则，其真值为-1。此时机器码再+1，则变为100000000。由于机器码只有八位，所以实际上机器码为00000000，即为0。所以此时机器码+1，真值也+1，符合环结构特征。

表示方法

综上，如果对原码作以下改动使其变为补码，则其结构符合环结构特征：

1、当符号为正，补码等于原码。

2、当符号为负，补码等于原码除符号位外按位取反再+1。

3、规定原码的10000000（-0）在补码中表示为-128，即 $2^{-7}$ 。

表示范围与特殊值

若字长为n,则补码的表示范围为 $[-2^{n-1},2^{n-1}-1]$ ，比原码多表示一个数。

补码需要记忆的特殊值如下：

+0=-0=00000000 -1=11111111 -128=10000000(占了原码中-0的坑) 127=01111111

移码

表示方法

移码就是在真值X上加上一个常数(偏置值),通常这个常数取 $2^{n-1}$ (字长为n),相当于X在数轴上向正方向偏移了若干单位,这就是“移码”一词的由来。移码的定义如下：

x移码=2^(n-1)+x

移码、原码与补码在机器数数轴上的差异如下图所示：

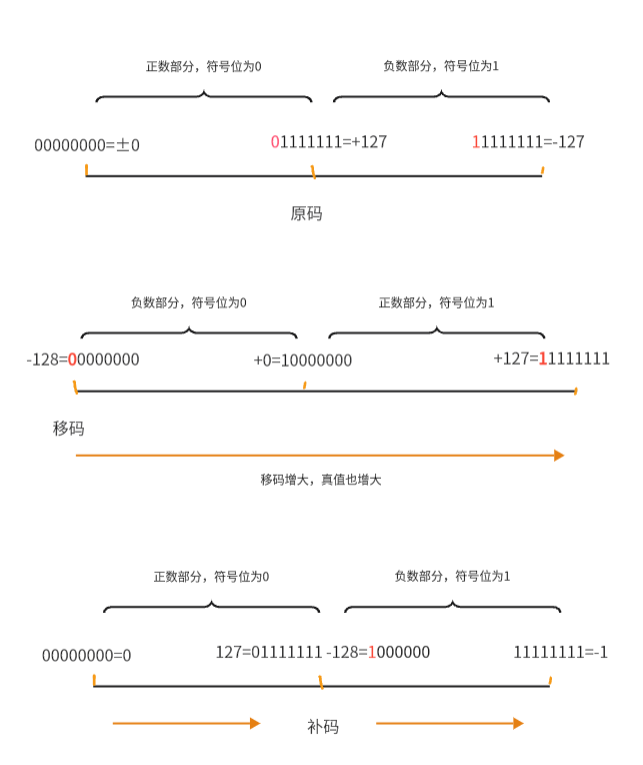
通过上图可以看到，移码越大真值越大，而原码与真值的变换关系在轴上不明确。事实上，移码与补码类似有相应的环结构特点（补码因为处于11111111时+1时最高位溢出所以和真值的对应关系没有移码这么清晰），他们之间的转换仅有符号位的差异，补码的符号位取反即为移码。

表示范围与特殊值

移码的表示范围和补码一样，为 $[-2^{n-1},2^{n-1}-1]$ 。

移码需要记忆的特殊值如下：

+0=-0=10000000 -128=00000000 127=11111111

三码辨析：各自的优点、缺点与适用场景

编码方式	优点	缺点	适用场景
原码	- 表示直观，最高位为符号位，数值部分为绝对值 - 易于理解	- 存在“+0”和“-0”两个表示 - 加减法运算复杂，需要区分符号	- 数据显示 - 人工理解与调试 - 教学引导
补码	- 只有一个0（无正负零） - 可将减法转化为加法，用统一的加法器实现加减运算 - 运算效率高，硬件实现简单	- 对人类不直观，不容易直接看出其代表的真值 - 表示范围略不对称（负数多一个）	- 计算机内部通用格式 - 算术运算（加减乘） - 整数寄存器和ALU操作
移码	- 所有数值都是非负数（适合排序、比较） - 符号位变为参与数值计算的一部分，便于与无符号数统一处理	- 加减法等运算不方便 - 需要额外偏移处理	- 浮点数阶码部分（IEEE 754标准） - 符号排序与比较操作