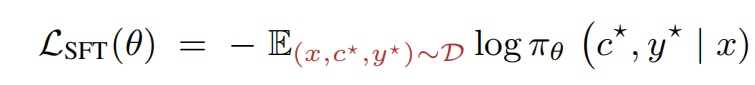自主学习-《Absolute Zero: Reinforced Self-play Reasoning with Zero Data》

1. 监督学习：需要人工给出推理过程；

2. RLVR: 推理过程由agent自我生成和学习，计算reward的gold值是环境或工具给出的，题目仍需要人工给出；

3. 本方法：题目也是agent自己生成的。（gold值仍需环境或工具给出）。

基本理论：

1. SFT的公式：（优化，使得input prompt x生成推理c*和结果y*的概率最大化）

痛点：模型吸收了足够多的知识后，没有更强的模型可供生成数据了，人工来标注数据又太费钱；

2. Reinforcement Learning with Verifiable Rewards的公式：（波浪线表示采样；y是模型采样得到的结果，y*是ground truth结果, r是reward function)

3. 本方法的公式：

示意图：

learnability: 模型训练了该样本之后，变强了多少；（太简单，模型每次都答对，则该样本没价值；太难，模型每次都打错，则该样本也没价值）

本文中，z这个随机变量，是用当前的题目集合中采样几个得到的题目集合；

流程图：

借助python这个工具，进行了对propose结果的learnability打分，进行了对solve结果的正确性打分。这2个分数，共同更新模型参数。

proposer的reward，就是多次solve(蒙特卡洛展开）取分数的平均值：

solver的reward，就是答对了还是答错了：

1. Buffer初始化

只用1个输入和输出都是"hello world"的极简python程序作为seed，多次迭代生成和完善新seed。

induction的program，是从另2个task的seed集合里选取的program。

2. propose

每次propose，放在prompt里的seed子集，都是变化的，采样自总seed集合。

prompt里明确强调：生成和seed不一样的program。

3. 样本过滤

3.1 <program,input>执行后，不抛异常，且有输出结果，则通过；

3.2 安全性：program不能使用敏感包（os.sys, sys, util等）

3.3 确定性：多跑几次，结果都一样，才通过；（为避免里面用了随机数）

注意：对于<i,o>生成p的任务, 只用一半<i,o>去生成p，用所有的<i,o>去验证生成的p是否正确。目的：防止生成if input1 then output1 elif input2 then output2这种取巧的program。

4 生成结果验证正确性：<p,i>生成o的任务，比对o和正确答案o是否相同即可；<p,o>生成i的任务，用p和生成的i去执行，判断o和正确答案o是否相同（因为生成同一个o的i可能有多组）；<i,o>生成p的任务，用p和所有的i依次生成o，判断o和正确答案o是否相同。

用的是python程序来判断，如下：

5. 优势函数，用的是相对的：

算法描述：

每轮(t)：生成一批样本（B=64个）。从总样本池里（不是本轮t生成的这B个），进行solve。计算reward，更新模型。

评测：

在Qwen2.5-7B和Qwen2.5-7B-coder的基础上，进行的训练，得到2个训练后的模型。

使用了coding和math两组评测集。

效果：两者上都有大的提升。（math评测集上的好效果，说明coding能力的提升，对general推理能力的提升是有帮助的）。比人工编写的coding训练数据上训出的SOTA模型，在coding能力上还要略有提升！

Qwen2.5-7B-coder上训练的模型，效果比Qwen2.5-7B上训练的模型，效果要更好。

In-Distribution: 大的模型，训练到后面还在提升；小的模型，效果曲线开始扁平下降；Out-of-Distribution: 越大的base模型，效果提升越大。

观察到的现象：1. <p,o>生成i任务时，反复从<p,i>推理结果，自我纠正，再更换i继续推理；2. <p,i>生成o任务时，跟踪代码，记录中间数据结构的值；3. <i,o,m>生成p任务时，每一条<i,o>都进行验证；其中1的例子：

生成代码任务，生成的代码中夹杂着step-by-step planning注释。

越训练，生成的token长度越长（DeepSeek等工作里也说过这个现象）。

消融实验（ablation studies）：3个task，选择性的去除某个或某几个，和没去除的，对比效果；结果显示，3个task都在，效果更好；

不使用动态采样例子放入prompt，则效果大幅下降；

让proposer不更新模型参数，只让solver更新模型参数，效果下降不大；

Prompt示例：

<p,i>生成o的任务，proposer:

<p,i>生成o的任务，solver: