洛谷 P2452 [SDOI2005] 屠龙传说-屠龙枪卷

题目描述

先知看到修玛取回的药草，满意地点了点头。

他对修玛说：“跟我来”。

修玛顺从地跟着先知走到了他的房间里。先知的房间很大，四周满是书架，整整齐齐地摆放着一排排书籍。房间中间的圆桌上摆放着一个巨大的水晶球，它发出的荧光照亮了整个房间。

先知走到一排书架前，从中抽出一本薄薄的书来。这本书看起来十分古老，纸张都变成了黄色，有的地方已经发黑。修玛想，这本书的历史大概有好几百年了吧。

先知示意修玛坐下，他翻开手中的书，对修玛说道：“我已经研究这本书很久了。它是用一种古老的文字写成的，记载了一个十分古老的传说。书中提到，普通的武器是无法伤害巨龙的，只有诸神合力锻造的屠龙枪才能消灭它。为了防止屠龙枪被滥用，神把它封印在卡基思山上，只有拥有超人的勇气、力量和智慧的人才能解开这个封印。千百年来，很多人都想得到屠龙枪的力量，然而从没有人成功过。我查阅了所有有关屠龙枪的记载，悉心地研究那些资料，得知屠龙枪被封印在山顶的神殿中，而要解开这道封印，就必须把神殿中的一块巨大的圆石推到神殿祭坛的中心，然后念出解开封印的咒语。”

修玛问道：“那句咒语应该已经失传了吧？”“不，恰恰相反。”先知说，“这句咒语一直记载在这本书中，并被完好地保存下来。”“那么，剩下的只是把圆石推到祭坛的中心了。”修玛自信地笑了。然而先知却摇了摇头，“不，修玛，事情没有你想象的那么简单。爬上卡基思山就不是一件容易的事。它高耸入云，四周都是光秃秃的石壁，几乎没有落脚的地方。只有真正的勇士才能爬得上去。那块圆石也不是那么容易就能推动的，非得有超常的力量不可。这些东西，修玛你都有。但如果仅仅只有这些，那么屠龙枪早已被人拿到手了。书中不是说了么，要有勇气、力量和智慧。智慧才是真正的关键。如果在固定时间内不能把那块圆石推到祭坛的中心，那么圆石便会自动滚回原处，同时推石的人将永远无法再次推动这块圆石。而且不管你用多大力气推，这块圆石都不可能滚动得像你希望的那样快，我估计只有按照最短路线去推这块圆石，才能在固定时间内把它推到祭坛中心。神殿中又有着大大小小的石柱，有些石柱与石柱之间的空隙很小，根本就推不过去。正因为这种种困难，才没有人能够从神殿中取走屠龙枪。”

修玛沉默了一会儿，说：“不管如何，我也要去试一试。如果我不能拿到屠龙枪，就没有人能够拿到它了。”

先知点了点头，说：“去吧，修玛。记住，用你的智慧。”

修玛骑马奔驰了十天十夜，终于来到了卡基思山脚下。正如先知所说的那样，这座山根本就没有路可以上去，甚至找不到可以落脚的地方。然而修玛凭着他的勇气以及熟练的技巧，爬上了山顶。

当他走进神殿，一眼就看到了那块巨大的圆石。修玛该怎么做，才能把圆石推到祭坛的中心呢？

任务

你的任务是计算出把圆石推到祭坛中心的最短路线长度。

所谓推到祭坛中心是指圆石的中心与祭坛中心重合。

圆石中心的初始位置以及祭坛中心的位置是已知的。圆石半径为 �R，它可以朝着任意方向滚动。洞中所有石柱均为正四棱柱，大小不一。

在推动圆石的过程中，要求圆石中心与所有石柱的距离均不小于 �R，否则圆石将被石柱阻挡而不能继续滚动。

输入格式

第一行包含了五个实数，依次表示圆石中心的初始位置的 �x 坐标、�y 坐标、圆石半径 �R、祭坛中心的位置 (�,�)(x,y)。

第二行包含一个整数 �n，表示神殿中石柱的数目。

接下来 �n 行，每行包含三个实数 (��,��,��)(xi​,yi​,ri​)，给出了一根石柱的信息，依次表示第 �i 根石柱左下角 �x 坐标、�y 坐标以及该石柱的边长。

数据输入所有实数均精确到 22 位小数，范围在 00 到 10001000 之内。

输出格式

输出仅包含一个实数，表示把圆石推到祭坛中心的最短路线长度，输出结果保留到两位小数。

若不存在一条把圆石推到祭坛中心的路，输出 0.00。

输入输出样例

输入 #1复制

0 0 10 30 40
1
10 10 10

输出 #1复制

57.93

说明/提示

数据范围及约定

对于全部数据，满足 0≤�≤200≤n≤20。

---

修玛思索良久，果断地走到圆石旁边，用力推动这块巨石。圆石在修玛的推动下，缓缓地滚动起来。修玛时不时地调整着推动的角度，以使巨石朝着自己希望的方向滚动。终于，“卡嗒”的一声，圆石安安稳稳地滚到了祭坛的中心。一束光从神殿顶上直射而下，笼罩了整个祭坛。修玛对着祭坛，大声地念出了解开封印的咒语。顿时，祭坛开始颤动，中间的圆石也随着摇摆不定。突然间，整块圆石完全爆裂开来，在祭坛的中心，出现了一柄长枪。枪身上闪烁着神圣的光芒，令人惊羡不已。修玛走上前去，拔起了这柄枪。他感到一股强大的力量从手上传了过来。修玛随手把枪一挥，只听得“哗啦”一声，一根巨大的石柱应声四分五裂了。修玛又惊又喜，他知道这一定就是屠龙枪。

本题给出若干个正方形障碍以及一个圆，求把圆推到目标位置的最短距离。

首先可以把这些障碍向外扩张 �r，形成一个类似

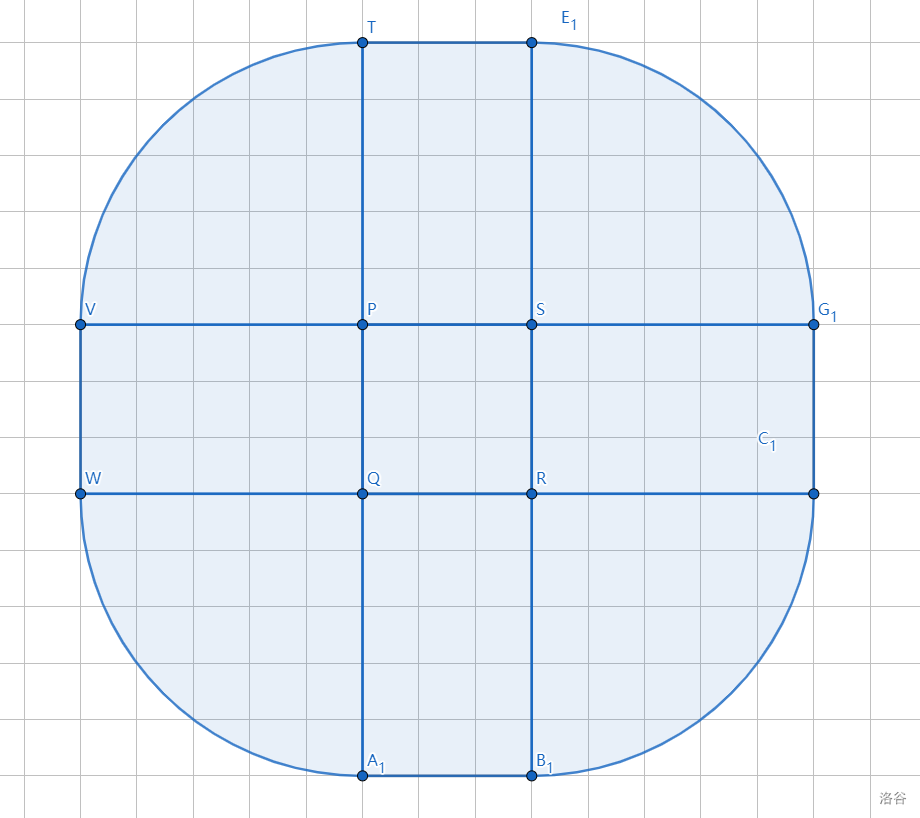
的图形，拆解开来就是 4 个圆加上俩矩形，将题意转化为从起点出发不穿过任意障碍到达终点的最短路。

先把样例画出来：

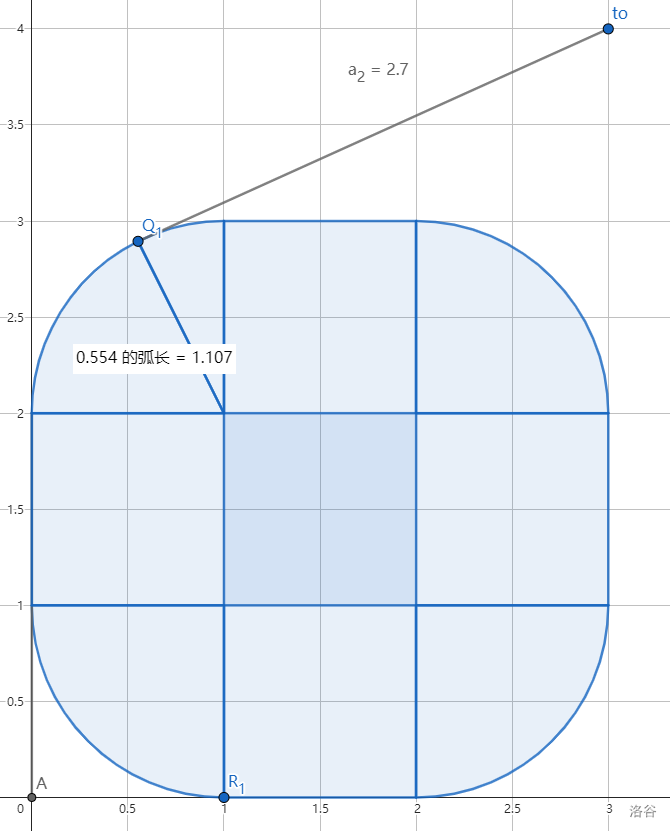
发现实际上可能走的路径分为四类：

1. 点到圆上的切点
2. 点直接到另一点
3. 同一圆上的点相互走
4. 圆到另一圆上的点

其中第 4 类实际上就是找到一条线段同时切两个圆，如下图的 ��CD 以及 ��FG。

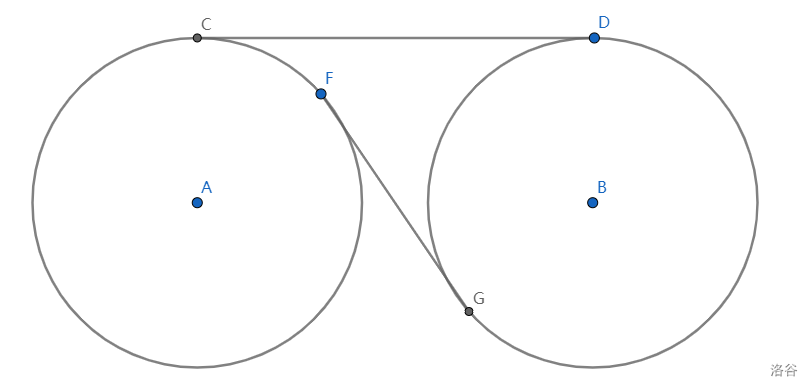
可以发现 ��⊥��AC⊥AB。

令 ��AB 中点为 �O，那么有 ��FO 切圆 �A 于 �F、��GO 切圆 �B 于 �G，套用 1 的方法即可找到 ��FG。

将所有的可能路径都 check 一遍，建出图跑最短路即可。要 check 的是一个线段或者一段圆弧是否穿过某个障碍。

线段是否穿过矩形内部

首先特判掉线段端点在矩形内部以及线段与矩形某条边重合的情况，然后再算出该线段与矩形四条边的交点个数 �x，当 �=2x=2 时线段穿过矩形。

线段是否穿过圆内部

求出线段到圆心的距离与半径比较一下即可。

圆弧是否穿过矩形内部

这个得画一画。令圆弧端点为 �,�l,r（逆时针），称一个点是合法的当且仅当该点不在 ��→ol 和 ��→or 组成的角内。

首先把圆弧上的端点在矩形内部特判掉，按照矩形端点在圆内部的点数 �m 以及圆心是否在矩形内部分讨。

• 圆心在矩形内部

  若有一个端点不在圆内部或圆上且该端点不合法，则圆弧穿过矩形内部。

• �=4m=4

  圆包含了矩形，肯定不穿过。

• �=1m=1

  

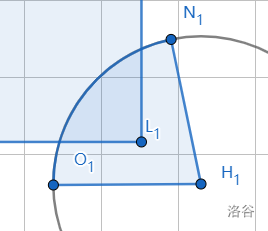
  当 �1L1​ 不合法时圆弧穿过矩形。

• �=2m=2

  

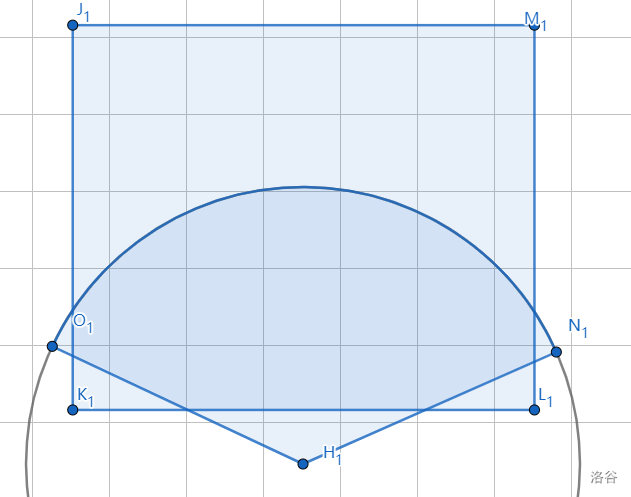
  当上面两个点有一个不合法时圆弧穿过矩形。

• �=3m=3

  

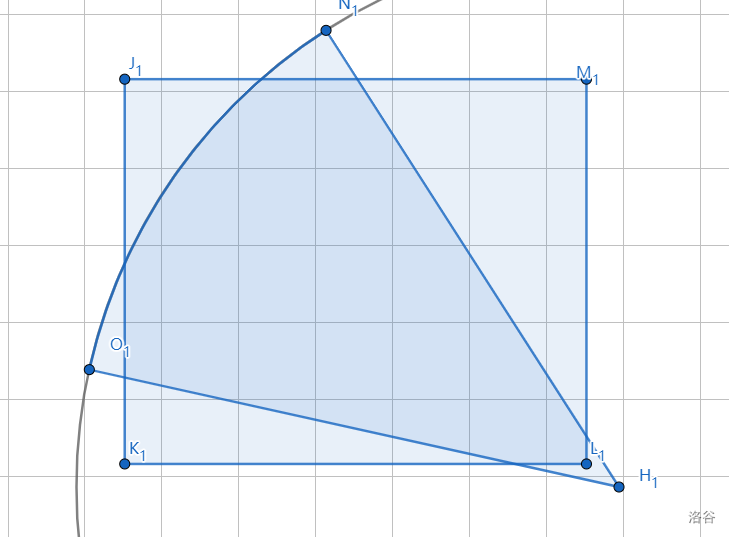
  剩下的那个点不合法就穿过。

• �=0m=0

  由于只会出现 1441​ 圆，故而不会出现只会包含一条边的情况，必定不穿过。

圆弧是否穿过圆内部

还是先特判两圆相离、圆弧端点在圆内的情况，若此时另一圆的圆心不合法则穿过。

代码如下:

#pragma GCC optimize("O2")
#include<bits/stdc++.h>
#define db double
#define seg(x,y) (line){x,y}
#define mk(x,y) (point){x,y}
using namespace std;
const int N=2e6+50;
const db eps=1e-6,pi=acos(-1),inf=1e32;void write(db x,char t='\n'){if(fabs(x)<eps)x=0;printf("%.2lf%c",x,t);}
template<class T, class... Args> inline void write(T x, Args... args) { write(x, ' '), write(args...); }struct point
{db x,y,k;friend point operator+(point a,point b){return mk(a.x+b.x,a.y+b.y);}friend point operator-(point a,point b){return mk(a.x-b.x,a.y-b.y);}friend point operator*(point a,db b){return mk(a.x*b,a.y*b);}db Atan2(){return atan2(y,x);}friend bool operator<(point a,point b){return a.k==b.k?a.x<b.x:a.k<b.k;}db len(){return sqrt(x*x+y*y);}void pre(point o){k=atan2(y-o.y,x-o.x);}friend bool operator==(point a,point b){a=a-b;return (fabs(a.x)<=eps)&(fabs(a.y)<=eps);}friend db dis(point a,point b){return (a-b).len();}friend point tolen(point a,db t){return a*(t/a.len());}void input(){scanf("%lf%lf",&x,&y);}void print(){printf("%.2lf %.2lf\n",x,y);}db angle(){return (y<0)*pi+atan(y/x);}point rotate(db t){return mk(x*cos(t)-y*sin(t),y*cos(t)+x*sin(t));}
}z,O;bool equiv(db x,db y){return fabs(x-y)<=eps;}
db dot(point a,point b){return a.x*b.x+a.y*b.y;}
db cross(point a,point b){return a.x*b.y-a.y*b.x;}
db angle(point a,point b){if(a==z||b==z)return 0;return acos(dot(a,b)/a.len()/b.len());}
point mirror(point a,point b){return b+(b-a);}
bool zcmp(db x){return fabs(x)<=eps;}struct line
{point a,b;point vec(){return b-a;}bool include(point x,int f=1){if(f)return zcmp(cross(a-x,b-x));if(!zcmp(cross(a-x,b-x)))return 0;return (min(a.x,b.x)<=x.x+eps)&(max(a.x,b.x)+eps>=x.x)&(min(a.y,b.y)<=x.y+eps)&(max(a.y,b.y)+eps>=x.y);}
};bool onright(line a,point s){return cross(a.a-s,a.b-s)<=0;}int relation(line a,line b)
{if(a.include(b.a)&&a.include(b.b))return -1;if(zcmp(cross(a.vec(),b.vec())))return 0;return 1;
}point intersect(line a,line b)
{db s1=cross(b.a-a.a,b.b-a.a),s2=cross(b.b-a.b,b.a-a.b);return a.a+(a.b-a.a)*(s1/(s1+s2));
}point perpend(line a,point b)
{point d=b+(a.vec()).rotate(pi/2);return intersect(a,(line){b,d});
}db dis(line a,point b,int f=1)
{if((a.a-a.b)==z)return -1;point p=perpend(a,b);if(a.include(p,0)||f)return dis(b,p);return min(dis(a.a,b),dis(a.b,b));
}int n,m,cs,cc;
point to,p[N];struct circle
{point o;db r;bool in(point x){return r>dis(x,o)+eps;}bool in(line x){return dis(x,o,0)+eps<r;}
}c[N],o;int intersectnum(line a,line b)
{if(relation(a,b)!=1)return 0;point x=intersect(a,b);return (a.include(x,0)&&b.include(x,0));
}struct square
{point a,dx,dy;bool in(point x){if(x.x>a.x+eps&&eps+x.x<(a+dx+dy).x&&x.y>a.y+eps&&eps+x.y<(a+dx+dy).y)return 1;return 0;}bool in(line x){if(in(x.a)||in(x.b))return 1;if(relation(seg(a,a+dx),x)==-1||relation(seg(a,a+dy),x)==-1||relation(seg(a+dx,a+dx+dy),x)==-1||relation(seg(a+dy,a+dx+dy),x)==-1)return 0;if(x.include(a)||x.include(a+dx)||x.include(a+dy)||x.include(a+dx+dy))return 0;int val=intersectnum(seg(a,a+dx),x)+intersectnum(seg(a,a+dy),x)+intersectnum(seg(a+dy,a+dy+dx),x)+intersectnum(seg(a+dx,a+dx+dy),x);return val==2;}bool chk(circle x){return x.in(seg(a,a+dx))|x.in(seg(a,a+dy))|x.in(seg(a+dx,a+dx+dy))|x.in(seg(a+dy,a+dx+dy));}
}s[N];bool chk(point x)
{for(int i=1;i<=cc;i++)if(c[i].in(x))return 1;for(int i=1;i<=cs;i++)if(s[i].in(x))return 1;return 0;
}bool chk(line x)
{for(int i=1;i<=cc;i++)if(c[i].in(x))return 1;for(int i=1;i<=cs;i++)if(s[i].in(x))return 1;return 0;
}bool chk(point o,point l,point r,point x)
{return onright(seg(o,r),x)&&!onright(seg(o,l),x);
}bool chk(circle o,point l,point r,circle x)
{if(dis(o.o,x.o)>=o.r+x.r)return 0;if(x.in(l)||x.in(r))return 1;return chk(o.o,l,r,x.o);
}bool chk(circle o,point l,point r,square x)
{if(x.in(l)||x.in(r))return 1;point a=x.a,b=a+x.dx,c=a+x.dy,d=a+x.dx+x.dy,t[6],q[6];int m=0,k=0;if(x.in(o.o)){if(dis(a,o.o)>o.r&&chk(o.o,l,r,a))return 1;if(dis(b,o.o)>o.r&&chk(o.o,l,r,b))return 1;if(dis(c,o.o)>o.r&&chk(o.o,l,r,c))return 1;if(dis(d,o.o)>o.r&&chk(o.o,l,r,d))return 1;return 0;}if(o.in(a))t[++m]=a;else q[++k]=a;if(o.in(b))t[++m]=b;else q[++k]=b;if(o.in(c))t[++m]=c;else q[++k]=c;if(o.in(d))t[++m]=d;else q[++k]=d;if(m==4)return 0;if(m==1)return chk(o.o,l,r,t[1]);if(m==2)return chk(o.o,l,r,q[1])|chk(o.o,l,r,q[2]);if(m==3)return chk(o.o,l,r,q[1]);if(!x.chk(o))return 0;return chk(o.o,l,r,a)+chk(o.o,l,r,b)+chk(o.o,l,r,c)+chk(o.o,l,r,d)>1;
}bool chk(circle o,point l,point r)
{for(int i=1;i<=cc;i++)if(chk(o,l,r,c[i]))return 1;for(int i=1;i<=cs;i++)if(chk(o,l,r,s[i]))return 1;return 0;
}db dis(circle o,point l,point r)
{r=r-o.o,l=l-o.o;return o.r*angle(l,r);
}struct edge
{int u,v;db w;int nxt;
}e[N];struct node
{int x;db w;friend bool operator<(node a,node b){return a.w>b.w;}
};int head[N],cnt;
db d[N];void add(int u,int v,db w)
{e[++cnt]=(edge){u,v,w,head[u]};head[u]=cnt;e[++cnt]=(edge){v,u,w,head[v]};head[v]=cnt;
}void dij()
{priority_queue<node>q;for(int i=1;i<=m;i++)d[i]=inf;d[1]=0;q.push((node){1,0});while(!q.empty()){int x=q.top().x;db w=q.top().w;q.pop();if(!equiv(w,d[x]))continue;for(int i=head[x];i;i=e[i].nxt){int v=e[i].v;if(d[v]>d[x]+e[i].w){d[v]=d[x]+e[i].w;q.push((node){v,d[v]});}}}if(equiv(d[2],inf))d[2]=0;cerr<<fixed<<setprecision(2)<<d[2]<<' ';
}point dx=mk(1,0),dy=mk(0,1);int find(circle o,point&a,point&b,point x)
{if(o.in(x))return 0;x=x-o.o;point rx=x;db angle=acos(o.r/x.len());x=tolen(x.rotate(angle),o.r);a=x+o.o;x=mirror(x,perpend(seg(O,rx),x));b=x+o.o;return 1;
}int h[N];bool cmp(int a,int b)
{return p[a]<p[b];
}vector<int>in[N];main()
{// freopen("in.txt","r",stdin);// freopen("out.txt","w",stdout);o.o.input(),scanf("%lf",&o.r);to.input();scanf("%d",&n);p[++m]=o.o,p[++m]=to;for(int i=1;i<=n;i++){point x;db r;x.input();scanf("%lf",&r);p[++m]=x-dx*o.r;p[++m]=x-dy*o.r;c[++cc]=(circle){x,o.r};in[cc].push_back(m),in[cc].push_back(m-1);x=x+dx*r;p[++m]=x+dx*o.r;p[++m]=x-dy*o.r;c[++cc]=(circle){x,o.r};in[cc].push_back(m),in[cc].push_back(m-1);x=x+dy*r;p[++m]=x+dx*o.r;p[++m]=x+dy*o.r;c[++cc]=(circle){x,o.r};in[cc].push_back(m),in[cc].push_back(m-1);x=x-dx*r;p[++m]=x-dx*o.r;p[++m]=x+dy*o.r;c[++cc]=(circle){x,o.r};in[cc].push_back(m),in[cc].push_back(m-1);x=x-dy*r;s[++cs]=(square){x-dx*o.r,dx*(2*o.r+r),dy*r};s[++cs]=(square){x-dy*o.r,dx*r,dy*(2*o.r+r)};}for(int i=1;i<=cc;i++)if(equiv(dis(p[1],c[i].o),c[i].r))in[i].push_back(1);for(int i=1;i<=cc;i++)if(equiv(dis(p[2],c[i].o),c[i].r))in[i].push_back(2);if(zcmp(o.r))cc=0;int mm=m;for(int i=1;i<=cc;i++)for(int j=i+1;j<=cc;j++){if(seg(O,dx).include(c[j].o-c[i].o))continue;if(seg(O,dy).include(c[j].o-c[i].o))continue;point x=c[j].o-c[i].o;x=x.rotate(pi/2);x=tolen(x,c[i].r);point A,B,C,D;A=c[i].o+x,B=c[i].o-x;C=c[j].o+x,D=c[j].o-x;if(!chk(seg(A,C)))p[++m]=A,p[++m]=C,add(m-1,m,dis(A,C)),in[i].push_back(m-1),in[j].push_back(m);if(!chk(seg(B,D)))p[++m]=B,p[++m]=D,add(m-1,m,dis(B,D)),in[i].push_back(m-1),in[j].push_back(m);}for(int i=1;i<=cc;i++)for(int j=i+1;j<=cc;j++){point x=c[j].o-c[i].o;x=c[i].o+tolen(x,x.len()*c[i].r/(c[i].r+c[j].r));point A,B,C,D;if(!find(c[i],A,B,x))continue;if(!find(c[j],C,D,x))continue;if(!zcmp(cross(A-x,C-x)))swap(A,B);if(!chk(seg(A,C)))p[++m]=A,p[++m]=C,add(m-1,m,dis(A,C)),in[i].push_back(m-1),in[j].push_back(m);if(!chk(seg(B,D)))p[++m]=B,p[++m]=D,add(m-1,m,dis(B,D)),in[i].push_back(m-1),in[j].push_back(m);}for(int i=1;i<=mm;i++)for(int j=1;j<=cc;j++)if(dis(p[i],c[j].o)>c[j].r){point x,y;if(!find(c[j],x,y,p[i]))continue;if(!seg(O,dx).include(p[i]-x)&&!seg(O,dy).include(p[i]-x)&&!chk(seg(p[i],x)))p[++m]=x,add(i,m,dis(p[i],x)),in[j].push_back(m);if(!seg(O,dx).include(p[i]-y)&&!seg(O,dy).include(p[i]-y)&&!chk(seg(p[i],y)))p[++m]=y,add(i,m,dis(p[i],y)),in[j].push_back(m);}for(int i=1;i<=cc;i++){int top=0;for(auto j:in[i])h[++top]=j,p[j].pre(c[i].o);sort(h+1,h+1+top,cmp);h[top+1]=h[1];for(int j=1;j<=top;j++)if(!chk(c[i],p[h[j]],p[h[j+1]]))add(h[j],h[j+1],dis(c[i],p[h[j]],p[h[j+1]]));}for(int i=1;i<=mm;i++)for(int j=i+1;j<=mm;j++)if(!chk(seg(p[i],p[j])))add(i,j,dis(p[i],p[j]));dij();
}

拜拜!