Transformer模型：多头注意力机制深度解析

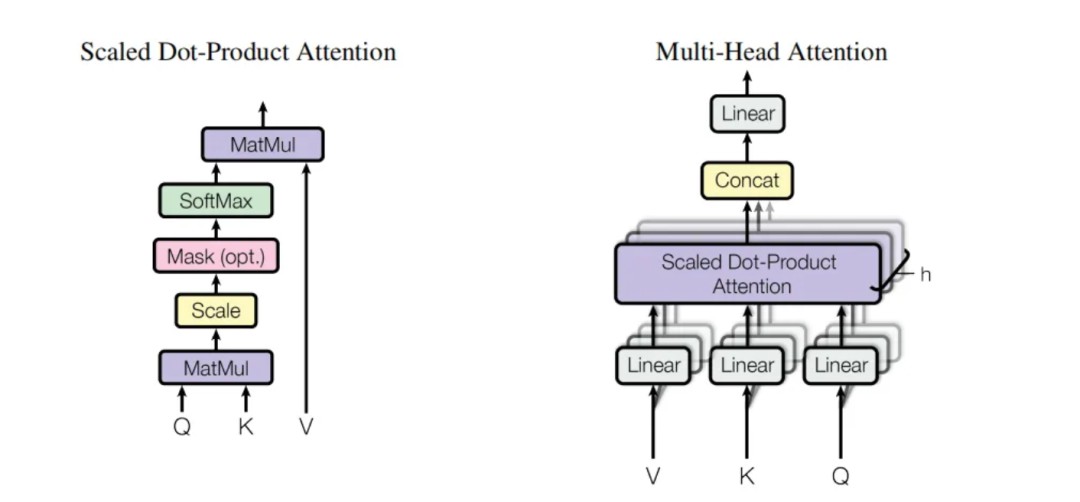
在多头注意力机制里，输入的查询（Query）、键（Key）和值（Value）会被投影到多个子空间（头）进行并行计算，每个头关注输入序列的不同方面。在所有头的注意力计算完成后，需要将这些头的结果拼接起来，然后通过一个线性层进行变换，以整合多头的信息，使其能够适应模型后续的计算需求。

 

一、线性层的定义

在PyTorch中，nn.Linear 类用于实现线性变换。当创建一个 nn.Linear 层时，会自动初始化一个权重矩阵W和一个偏置向量b。在 MultiHeadedAttention 类中，self.linears 是一个包含 4 个线性层的列表，其中 self.linears[-1] 是最后一个线性层，用于最终的线性变换。

class MultiHeadedAttention(nn.Module):    def __init__(self, h, d_model, dropout=0.1):        # ...        #- 4 线性层的列表        #- 线性层的输入和输出的维度都是 d_model        self.linears = clones(nn.Linear(d_model, d_model), 4)        # ...
    def forward(self, query, key, value, mask=None):        # ...        x = (            x.transpose(1, 2)            .contiguous()            .view(nbatches, -1, self.h * self.d_k)        )        # ...        return self.linears[-1](x)  

nn.linear的解释：
1.用于实现线性变换（也称为全连接层）的基础模块，其底层实现基于张量操作和自动微分系统。
2. 线性变换的数学表达式为：y = xW^T + b。其中：
x 是输入张量，形状为 [..., in_features]
W 是可学习的权重矩阵，形状为 [out_features, in_features]
b 是可学习的偏置向量，形状为 [out_features]
y 是输出张量，形状为 [..., out_features]
3. 实现步骤：
(1) 参数初始化在创建nn.Linear(in_features, out_features) 时，会初始化：
权重矩阵 W：形状为 [out_features, in_features]，通常用随机值初始化（如 Xavier 或 Kaiming 初始化）。
偏置向量 b：形状为 [out_features]，通常初始化为零。 
(2) 前向传播前向传播时，输入张量x会与权重矩阵W相乘，并加上偏置 b。矩阵乘法：x dot W^；添加偏置：结果加上 b。

(3) 自动微分PyTorch 的自动微分系统会跟踪 W和b的梯度，以便在反向传播时更新参数。  

二、Q、K、V线性变换

 

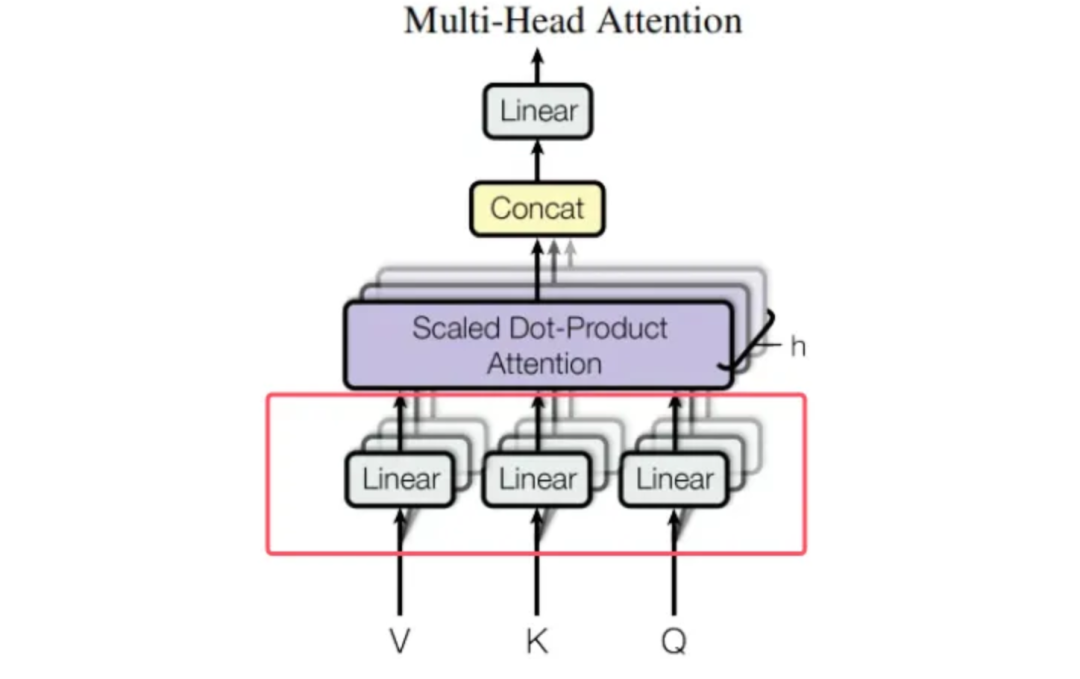
“我”“爱”“AI” 这三个经过词嵌入和位置编码后的输入向量，会分别通过与三个不同的权重矩阵W^Q、W^K 和W^V相乘来得到查询（Query）、键（Key）和值（Value）。

在模型中，通过线性层（神经网络）完成的，每个线性层都相当于一个可学习的权重矩阵。

下面详细解释它们之间的关系：

1. 输入向量的生成

“我爱 AI” 经过分词得到 “我”“爱”“AI”，对这些词进行词嵌入操作，将每个词映射为一个固定维度的向量。为了让模型能够感知词的位置信息，还会对这些词嵌入向量添加位置编码，最终得到 “我”“爱”“AI” 对应的三个输入向量。假设这些输入向量的维度为d_model（通常在 Transformer 中其值为512。

2. 线性投影的作用

在多头注意力机制中，为了让模型能够从不同的子空间关注输入序列的不同方面，需要将输入向量分别投影到查询、键和值的空间中。这是通过与三个不同的权重矩阵W^Q、W^K 和W^V相乘来实现的。

3. 具体的线性投影过程

在 the_annotated_transformer.py 文件中的 MultiHeadedAttention 类里，线性投影的实现如下：

class MultiHeadedAttention(nn.Module):    def __init__(self, h, d_model, dropout=0.1):        # ... 初始化代码 ...        self.linears = clones(nn.Linear(d_model, d_model), 4)        # ... 其他代码 ...
    def forward(self, query, key, value, mask=None):        # ... 其他代码 ...        query, key, value = [            lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)            for lin, x in zip(self.linears, (query, key, value))        ]        # ... 其他代码 ...

这里的 self.linears 包含了用于线性投影的线性层，其中前三个线性层分别对应 W^Q、W^K 和W^V。具体步骤如下： • 对 “我”“爱”“AI” 的输入向量进行投影： ◦ 假设 “我”“爱”“AI” 对应的输入向量分别为x1、x2、x3，它们的维度都是 d_model。 ◦ 对于查询向量 Q，将输入向量 x1、x2、x3 与 W^Q相乘，得到对应的查询向量q1、q2、q3。 ◦ 对于键向量 K，将输入向量x1、x2、x3 与 W^K相乘，得到对应的键向量 k1、k2、k3。 ◦ 对于值向量 V，将输入向量x1、x2、x3与 W^V相乘，得到对应的值向量v1、v2、v3。 • 多头处理：在得到查询、键和值向量后，还会将它们拆分为多个头（在 Transformer 中通常为 8 个头），以便并行计算。

小结

“我”“爱”“AI” 这三个经过词嵌入和位置编码后的输入向量，会分别与W^Q、W^K 和W^V相乘，得到对应的查询、键和值向量，用于后续的多头注意力计算。这样做可以让模型从不同的子空间关注输入序列的不同方面，提高模型的表达能力。

三、拼接后线性变换

 

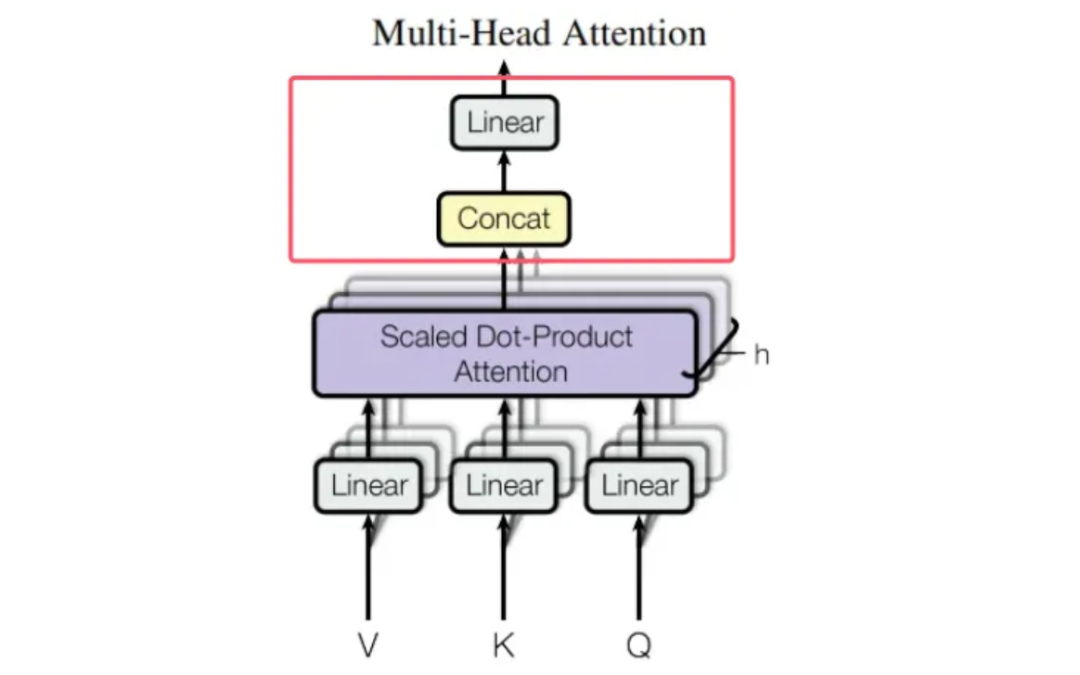
在多头注意力机制里，Concat（拼接）操作的目的是将多个头的注意力结果合并成一个张量，之后再通过一个线性层进行变换。  在 MultiHeadedAttention 类的 forward 方法里，Concat 操作是通过形状重塑和转置达成的。以下是相关代码：

class MultiHeadedAttention(nn.Module):    def __init__(self, h, d_model, dropout=0.1):        # ... 初始化代码 ...        self.linears = clones(nn.Linear(d_model, d_model), 4)        # ... 其他代码 ...
    def forward(self, query, key, value, mask=None):        # ... 其他代码 ...        # 1) 进行线性投影        query, key, value = [            lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)            for lin, x in zip(self.linears, (query, key, value))        ]
        # 2) 应用注意力机制        x, self.attn = attention(            query, key, value, mask=mask, dropout=self.dropout        )
        # 3) "Concat" 操作        x = (            x.transpose(1, 2)            .contiguous()            .view(nbatches, -1, self.h * self.d_k)        )        del query        del key        del value        return self.linears[-1](x)
 *******************        拼接操作步骤 ******************* 1. 转置维度：x = x.transpose(1, 2)    #-将头的维度和序列长度维度进行交换，使x的形状变为 (nbatches, seq_len, self.h, self.d_k)。 2. 确保内存连续：x = x.contiguous()   3. 重塑形状：x = x.view(nbatches, -1, self.h * self.d_k)    #-将多个头的结果拼接在一起，x的形状变为 (nbatches, seq_len, self.h * self.d_k)    #-self.h 代表头（head）的数量，self.d_k 是每个头的维度。    #-self.h * self.d_k 这一操作是为了算出所有头拼接后的总维度。    #-这个维度实际上等同于模型的总维度d_model
*********************线性变换*********************   return self.linears[-1](x)#-线性层 self.linears[-1] 用于对拼接后的结果进行线性变换#-self.linears[-1](x) 把拼接后的结果 x 传入最后一个线性层#-线性层中的可学习权重矩阵 W
*********************权重矩阵*********************1. 含义：   权重矩阵W是一个可学习的参数，它的作用是将拼接后的结果   从一个 d_model 维的向量空间映射到另一个 d_model 维的向量空间。   在训练过程中，模型会根据输入数据自动调整 W 的值，以学习到最优的映射关系。2. 线性层的工作原理示例代码import torchimport torch.nn as nn
# 假设 d_model = 512d_model = 512# 创建一个线性层linear_layer = nn.Linear(d_model, d_model)
# 输入张量，形状为 (batch_size, seq_len, d_model)batch_size = 32seq_len = 10x = torch.randn(batch_size, seq_len, d_model)
# 进行线性变换y = linear_layer(x)
# 查看输出形状print("输入形状:", x.shape)  # 输出: torch.Size([32, 10, 512])print("输出形状:", y.shape)  # 输出: torch.Size([32, 10, 512])
# 查看权重矩阵 W 和偏置向量 b 的形状W = linear_layer.weightb = linear_layer.biasprint("权重矩阵 W 的形状:", W.shape)  # 输出: torch.Size([512, 512])print("偏置向量 b 的形状:", b.shape)  # 输出: torch.Size([512])

拼接（Concat）后进行线性变换的主要目的是让模型能够学习如何整合不同头的信息，并将其映射到一个更有意义的表示空间。这一步骤是多头注意力设计的核心，下面从原理和代码两方面详细解释。

1. 拼接操作的局限性在多头注意力中，输入会被投影到多个子空间（头），每个头关注输入的不同方面。例如： 

• 一个头可能关注主语和谓语的关系。

• 另一个头可能关注实体之间的语义关联。当所有头的计算完成后，直接拼接这些结果只是简单地将不同视角的信息堆叠在一起，但并没有让模型学习如何融合这些信息。此时的输出只是多个子空间表示的罗列，缺乏整体的语义整合。

2. 线性变换的作用拼接后的线性变换（即代码中的 self.linears[-1]）通过一个可学习的权重矩阵 W 和偏置向量 b，让模型能够：

（1）整合多头信息：学习不同头之间的关联和权重，将分散的子空间表示融合为一个统一的表示。

（2）增加模型表达能力：线性变换引入了额外的参数，使模型能够学习更复杂的映射关系。

（3）保持维度一致性：确保输出维度与输入维度相同（即 d_model），便于后续层的处理。