MGAug：图像变形潜空间中的多模态几何增强|文献速递-深度学习医疗AI最新文献

Title

题目

MGAug: Multimodal Geometric Augmentation in Latent Spaces of ImageDeformations

MGAug：图像变形潜空间中的多模态几何增强

01

文献速递介绍

近年来，深度学习（DL）在图像分析任务中取得了显著进展，包括但不限于图像分类（Krizhevsky等，2017；Wang和Zhang，2022；Hossain等，2024）、分割（Hossain等，2019；Chen等，2021）、目标检测（Kim和Pavlovic，2016；Pang等，2019）和3D重建（Jayakumar等，2023）。研究表明，深度神经网络（DNN）在大量人工标注数据上训练时表现最佳。然而，由于隐私问题、法规限制、成本和疾病病例稀缺等原因，许多图像应用领域可用的标注数据集相对较小。在这种情况下，DNN往往因对数据变化的泛化能力不足而出现过拟合现象。数据增强（DA）是一种简单、高效且常用的策略，通过合成更多训练样本来人为扩大数据集规模（Cubuk等，2019；Zhao等，2019；Shen等，2020；Zoph等，2020）。它通常作为训练数据的预处理步骤，使DNN能够学习各种近似不变性，从而减少过拟合问题。在图像领域，常见的增强策略包括对图像强度进行变换（Chaitanya等，2019，2021；Gao等，2021；Hesse等，2020；Zhao等，2023），或通过随机生成的几何变换（如平移、旋转或缩放）对图像进行变形（Moreno-Barea等，2018）。基于强度的增强方法在严重依赖颜色和纹理信息的任务中特别有价值，而几何变换则能生成多样化、逼真的场景，为训练数据引入结构变化。这种训练数据的多样性提高了模型的泛化能力，因为模型学会了识别关键特征而不依赖于它们的空间排列。本文主要关注DA，特别是在表征图像中物体可变形形状（变化）的几何空间中的DA（Joshi等，2004；Beg等，2005；Zhang等，2013；Zhang和Fletcher，2015；Dalca等，2019b）。 在实践中，几何DA通常是一个手动过程，由人工指定一组认为能使DL模型具有不变性的仿射或可变形变换（Hendrycks等，2019；Yun等，2019）。然而，这种方法可能会产生不真实或不合理的图像变体。例如，将自然图像旋转180度是有意义的，但对数字图像（如数字'6'和'9'）则会产生歧义。在医学领域，随机生成的变形可能会将健康图像转换为疾病图像。为缓解这些问题，研究人员开发了一组自动DA方法，这些方法从数据本身学习最优增强策略（Cubuk等，2019；Lim等，2019；Zoph等，2020；Araslanov和Roth，2021；Muralikrishnan等，2022）。尽管这些方法在相对简单的数据集（如MNIST）上显示出令人鼓舞的结果，但它们似乎不适用于具有较大结构和几何变化的复杂数据集。 后来，生成模型（如VAE）被广泛用作在数据有限的情况下捕获复杂几何变化的实用有效解决方案（Moreno-Barea等，2020；Li等，2019；Pesteie等，2019；Tang等，2020）。在DA中使用VAE的基本原理在于它们能够学习和表示数据的潜在特征。通过从学习到的潜在空间中采样，VAE可以生成超出训练数据集范围的多样化且逼真的合成数据样本。此外，在DA的背景下，VAE通常不负责学习整个数据分布，而是生成与原始数据集分布一致的合成数据样本（Chadebec和Allassonnière，2021；Chadebec等，2022；Muralikrishnan等，2022）。 另一种常见方法是学习从训练图像导出的一组可变形变换的概率分布（Hauberg等，2016；Krebs等，2019；Dalca等，2019a；Zhao等，2019；Olut等，2020；Shen等，2020）。然而，这些方法假设图像间潜在变换服从单峰分布，无法提供学习训练数据中几何变换完整空间的适当方式。当处理自然具有多峰分布的多模态数据时，如时间序列数据/纵向图像（Di Martino等，2014；LaMontagne等，2019）或包含亚群体的图像（如涉及健康与疾病群体的人群研究，Jack Jr.等，2008；LaMontagne等，2019），这种局限性尤为明显。 本文提出了一种新型模型MGAug，首次在几何变形的多模态潜在空间中学习增强变换。受混合模型启发，该模型通过捕获群体图像变形的潜在分布，改进了群体研究分析（Zhang等，2015，2019；Luo和Zhuang，2020；Hertz等，2020）。MGAug的主要优势在于： 1. 将自动DA过程推广到允许隐藏多模态变换的几何空间； 2. 开发一种新的生成模型，通过在微分同胚切空间中定义的多元高斯混合先验学习增强变换的潜在分布； 3. 利用组内约束从训练数据本身的知识中提升增强样本的质量。 为实现这一目标，我们首先开发了一个深度学习网络，通过基于模板的图像配准将微分同胚变换的潜在几何空间学习嵌入VAE中。在微分同胚的切空间中定义多元高斯混合模型，并作为VAE潜在空间的先验。然后，通过对从学习到的多模态分布中随机采样的解码速度场对图像进行变形，增强原始训练数据集。我们在两个不同的领域特定任务中验证了模型的有效性：2D合成数据和真实3D脑磁共振图像（MRI）的多分类与分割任务。我们还将MGAug与基于变换的最先进增强算法（Olut等，2020；Dalca等，2019a）进行了比较。实验结果表明，我们的方法通过显著提高预测精度优于所有基线算法。 本文的其余部分组织如下：第2节讨论基于模板的图像配准的几何变形背景；第3节介绍我们提出的增强算法MGAug的方法发展及联合优化方案；第4节讨论在不同图像分析任务上验证模型有效性的实验评估；第5节总结并提出潜在的未来研究方向。

Abatract

摘要

Geometric transformations have been widely used to augment the size of training images. Existing methodsoften assume a unimodal distribution of the underlying transformations between images, which limits theirpower when data with multimodal distributions occur. In this paper, we propose a novel model, MultimodalGeometric Augmentation* (MGAug), that for the first time generates augmenting transformations in a multimodallatent space of geometric deformations. To achieve this, we first develop a deep network that embeds thelearning of latent geometric spaces of diffeomorphic transformations (a.k.a. diffeomorphisms) in a variationalautoencoder (VAE). A mixture of multivariate Gaussians is formulated in the tangent space of diffeomorphismsand serves as a prior to approximate the hidden distribution of image transformations. We then augmentthe original training dataset by deforming images using randomly sampled transformations from the learnedmultimodal latent space of VAE. To validate the efficiency of our model, we jointly learn the augmentationstrategy with two distinct domain-specific tasks: multi-class classification on both synthetic 2D and real 3Dbrain MRIs, and segmentation on real 3D brain MRIs dataset. We also compare MGAug with state-of-the-arttransformation-based image augmentation algorithms. Experimental results show that our proposed approachoutperforms all baselines by significantly improved prediction accuracy. Our code is publicly available atGitHub.

几何变换已被广泛用于扩大训练图像的规模。现有方法通常假设图像间潜在变换的单峰分布，这使其在处理具有多峰分布的数据时能力受限。在本文中，我们提出了一种新型模型多模态几何增强（MGAug），该模型首次在几何变形的多模态潜空间中生成增强变换。   为实现这一目标，我们首先开发了一个深度网络，将微分同胚变换（即diffeomorphisms）的潜几何空间学习嵌入到变分自编码器（VAE）中。在微分同胚的切空间中构造多元高斯混合模型，作为先验来近似图像变换的隐藏分布。随后，我们通过从VAE学习到的多模态潜空间中随机采样变换对图像进行变形，从而增强原始训练数据集。   为验证模型的有效性，我们将增强策略与两项不同的领域特定任务结合学习：合成2D和真实3D脑MRI的多分类任务，以及真实3D脑MRI数据集的分割任务。我们还将MGAug与最先进的基于变换的图像增强算法进行了比较。实验结果表明，我们提出的方法通过显著提高预测精度，优于所有基线方法。我们的代码已在GitHub上公开。

Background

背景

 我们首先简要回顾基于模板的可变形图像配准（Joshi 等，2004；Zhang 等，2013）的概念，该方法广泛用于从群体图像中估计可变形的几何变形。在这项工作中，我们采用大变形微分同胚度量映射（LDDMM）算法，该算法可确保变形场的平滑性并保留图像的拓扑结构（Beg 等，2005）。   给定一组 ( N ) 幅图像 ({I_1, \dots, I_N})，基于模板的图像配准问题旨在找到模板图像 ( I ) 与其余图像数据之间的最短路径（即测地线），并推导相关的变形场 ({\phi_1, \dots, \phi_N})，以最小化能量函数：   [ E(I, \phi_n) = \sum{n=1}^N \frac{1}{2\sigma^2} \text{Dist}[I \circ \phi_n(v_n(t)), I_n] + \text{Reg}[\phi_n(v_n(t))], ]   （1）   其中 (\sigma^2) 是噪声方差，(\circ) 表示通过估计的变换 (\phi_n) 对图像 ( I ) 进行变形的插值操作。(\text{Dist}[\cdot, \cdot]) 是衡量图像间差异的距离函数，例如平方差和（Beg 等，2005）、归一化互相关（Avants 等，2008）和互信息（Wells III 等，1996）。(\text{Reg}[\cdot]) 是正则化项，用于保证变换的平滑性，即：   [ \text{Reg}[\phi_n(v_n(t))] = \int_0^1 (Lv_n(t), v_n(t)) \, dt, ]   其中：   [ \frac{d\phi_n(t)}{dt} = v_n(t) \circ \phi_n(t), ]   （2）   这里 ( L: V \to V^* ) 是对称正定微分算子，将切向量 ( v_n(t) \in V ) 映射到其对偶空间的动量向量 ( m_n(t) \in V^* )。我们记 ( m_n(t) = Lv_n(t) ) 或 ( v_n(t) = Km_n(t) )，其中 ( K ) 是 ( L ) 的逆算子。算子 ( D ) 表示雅可比矩阵，(\cdot) 表示矩阵元素级乘法。在本文中，我们使用形式为 ( L = -\alpha\Delta + I ) 的度量，其中 (\Delta) 是离散拉普拉斯算子，(\alpha) 是正正则化参数，(I) 表示单位矩阵。   通过求解给定初始速度场条件 ( v_n(0) ) 的欧拉-庞加莱微分方程（EPDiff）（Arnold，1966；Miller 等，2006），可唯一确定方程（2）的最小值：   [ \frac{\partial v_n(t)}{\partial t} = -K\left[(Dv_n(t))^T \cdot m_n(t) + Dm_n(t) \cdot v_n(t) + m_n(t) \cdot \text{div } v_n(t)\right], ]   （3）   其中算子 ( D ) 表示雅可比矩阵，(\text{div}) 是散度算子，(\cdot) 表示元素级矩阵乘法。这被称为测地线射击算法（Vialard 等，2012），该算法很好地证明了基于变形的形状描述符 (\phi_n) 可以完全由初始速度场 ( v_n(0) ) 表征。   因此，我们可以将方程（1）中的能量函数等价地最小化为：   [ E(I, v_n(0)) = \sum{n=1}^N \frac{1}{2\sigma^2} \text{Dist}[I \circ \phi_n(v_n(0)), I_n] + (Lv_n(0), v_n(0)), \quad \text{s.t. 方程（3）}. ]   （4）   为简化符号，以下章节将省略时间索引。   许多研究工作将初始速度场 (\tilde{v}_n) 的先验定义为多元高斯分布，以确保测地线路径的平滑性（Zhang 等，2013，2016；Wang 和 Zhang，2021）。该先验通常表示为：   [ p(v_n) = \frac{1}{(2\pi)^{M/2} |L^{-1}|^{1/2}} \exp\left(-\frac{1}{2}(Lv_n, v_n)\right), ]   （5）   其中 ( M ) 表示初始速度的体素总数，(|\cdot|) 是矩阵行列式。需要注意的是，这里我们假设输入图像是在离散网格上测量的，即图像是有限维欧几里得空间的元素。我们还假设速度场和由此产生的微分同胚定义在离散网格上，这使得我们可以在通过微分算子 ( L ) 保持速度场平滑性的同时，处理定义良好的概率密度函数。在实践中，我们采用离散化算子 ( L )（如方程（2）中先前定义）（Beg 等，2005；Vialard 等，2012；Zhang 等，2013）。(|L^{-1}|) 指离散微分算子逆的行列式。

Method

方法

This section presents a novel algorithm, MGAug, that learns a multimodal latent distribution of geometric transformations represented bythe initial velocity fields 𝑣0 . We first introduce a generative model inlatent geometric spaces for DA based on VAE, followed by an approximated variational inference. The augmented data is then used to trainvarious image analysis tasks, i.e., image classification or segmentation.Similar to Zhao et al. (2019), Chen et al. (2022), we employ a jointlearning scheme to optimize the MGAug and image analysis tasks (IAT)network parameters. To simplify the notation, we omit the time indexof 𝑣0 in the following sections.

本节提出了一种新算法MGAug，该算法学习由初始速度场 ( v_0 ) 表示的几何变换的多模态潜在分布。我们首先介绍基于变分自编码器（VAE）的生成模型，用于数据增强（DA）的潜在几何空间学习，随后进行近似变分推理。增强后的数据将用于训练各种图像分析任务，如图像分类或分割。与Zhao等人（2019）、Chen等人（2022）类似，我们采用联合学习方案来优化MGAug和图像分析任务（IAT）的网络参数。为简化符号，以下章节将省略 ( v_0 ) 的时间索引。

Conclusion

结论

In this paper, we present a novel data augmentation model, MGAug,which learns augmenting transformations in a multimodal latent spaceof geometric deformations. In contrast to existing augmentation modelsthat adopt a unimodal distribution to augment data, our augmentation method fully characterizes the multimodal distribution of imagetransformations via introducing a mixture of multivariate Gaussians asthe prior. Our method significantly improves the performance of multiclass classification (on 2D datasets) and image segmentation (on 3Dbrain MRIs) and eliminates the artifacts of geometric transformationsby preserving the topological structures of augmented images. WhileMGAug focuses on LDDMM, the theoretical tool developed in our modelis widely applicable to various registration frameworks, for example,stationary velocity fields (Modat et al., 2012; Hadj-Hamou et al., 2016).To the best of our knowledge, we are the first to learn geometricdeformations in a multimodal manner via deep neural networks. Ouraugmentation model can be easily applied to different domain-specifictasks, e.g., image reconstruction and object tracking. Interesting future directions based on this work can be (i) investigating the modelinterpretability for classification tasks when geometric deformationsare learned in a multimodal manner, and (ii) the robustness study ofMGAug when image intensity variations occur, i.e., under adversarialnoise attacks.

在本文中，我们提出了一种新颖的数据增强模型MGAug，该模型在几何变形的多模态潜空间中学习增强变换。与现有采用单峰分布进行数据增强的模型不同，我们的增强方法通过引入多元高斯混合作为先验，充分刻画了图像变换的多模态分布。我们的方法显著提升了多分类任务（在2D数据集上）和图像分割任务（在3D脑MRI上）的性能，并通过保留增强图像的拓扑结构消除了几何变换的伪影。尽管MGAug聚焦于LDDMM（大变形微分同胚度量映射），但我们模型中开发的理论工具可广泛应用于各种配准框架，例如平稳速度场（Modat等，2012；Hadj-Hamou等，2016）。 据我们所知，我们首次通过深度神经网络以多模态方式学习几何变形。我们的增强模型可轻松应用于不同的领域特定任务，如图像重建和目标跟踪。基于这项工作，有趣的未来研究方向包括：（i）研究当以多模态方式学习几何变形时，分类任务的模型可解释性；（ii）研究MGAug在图像强度变化（如对抗噪声攻击）下的鲁棒性。

Figure

图

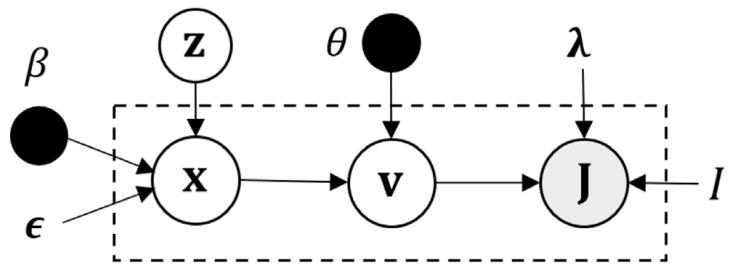
Fig. 1. Graphical representation of our proposed generative model in multimodalgeometric latent space.

图1. 所提出的多模态几何潜空间生成模型的图示。

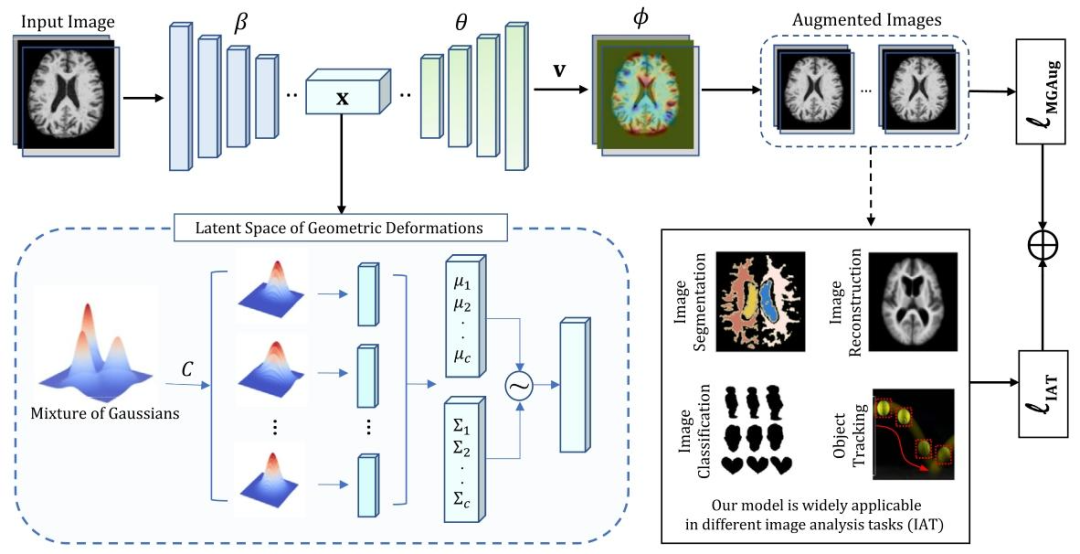
Fig. 2. An overview of our model MGAug for image analysis tasks.

图2. 用于图像分析任务的MGAug模型概览。

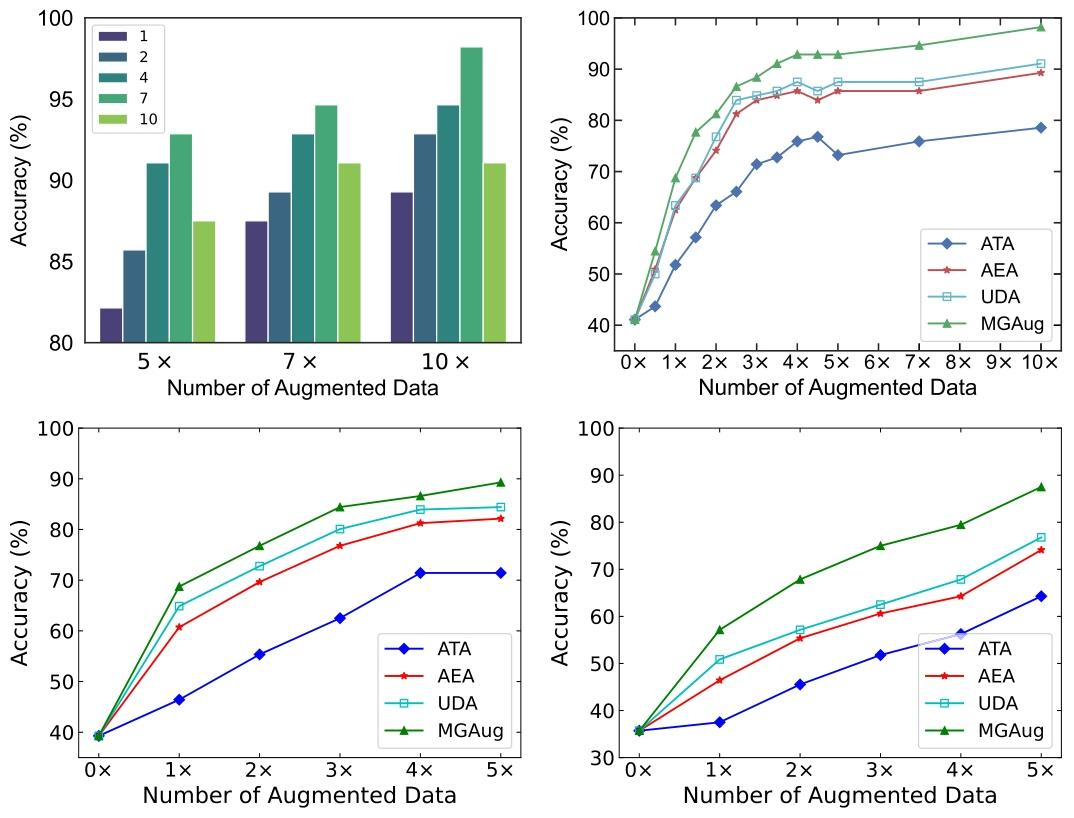
Fig. 3. Left: Accuracy comparison on various modes 𝐶 on 2D shape dataset. Right: A comparison of classification performance for all models over increasing number of augmenteddata taking all (top-right), 75% (bottom-left), and 50% (bottom-right) ground truth images

图3 左图：2D形状数据集上不同模式数𝐶的准确率对比。右图：使用全部（右上）、75%（左下）和50%（右下）真实标注图像时，各模型在增强数据量增加情况下的分类性能对比。

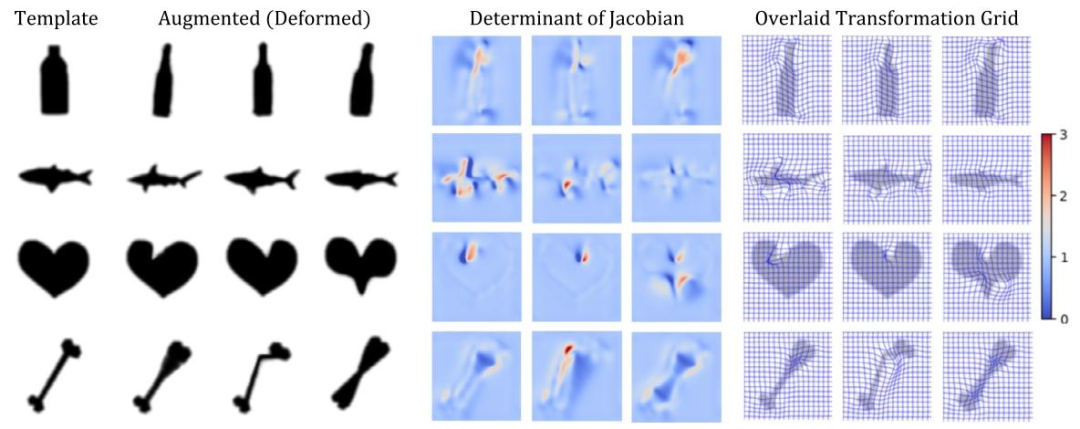
Fig. 4. Examples of DetJac generated by MGAug. Left to right: template, augmented (deformed), DetJac overlaid with augmented images.

图4. MGAug生成的DetJac示例。从左到右：模板图像、增强（变形）图像、叠加在增强图像上的DetJac（行列式雅可比）。

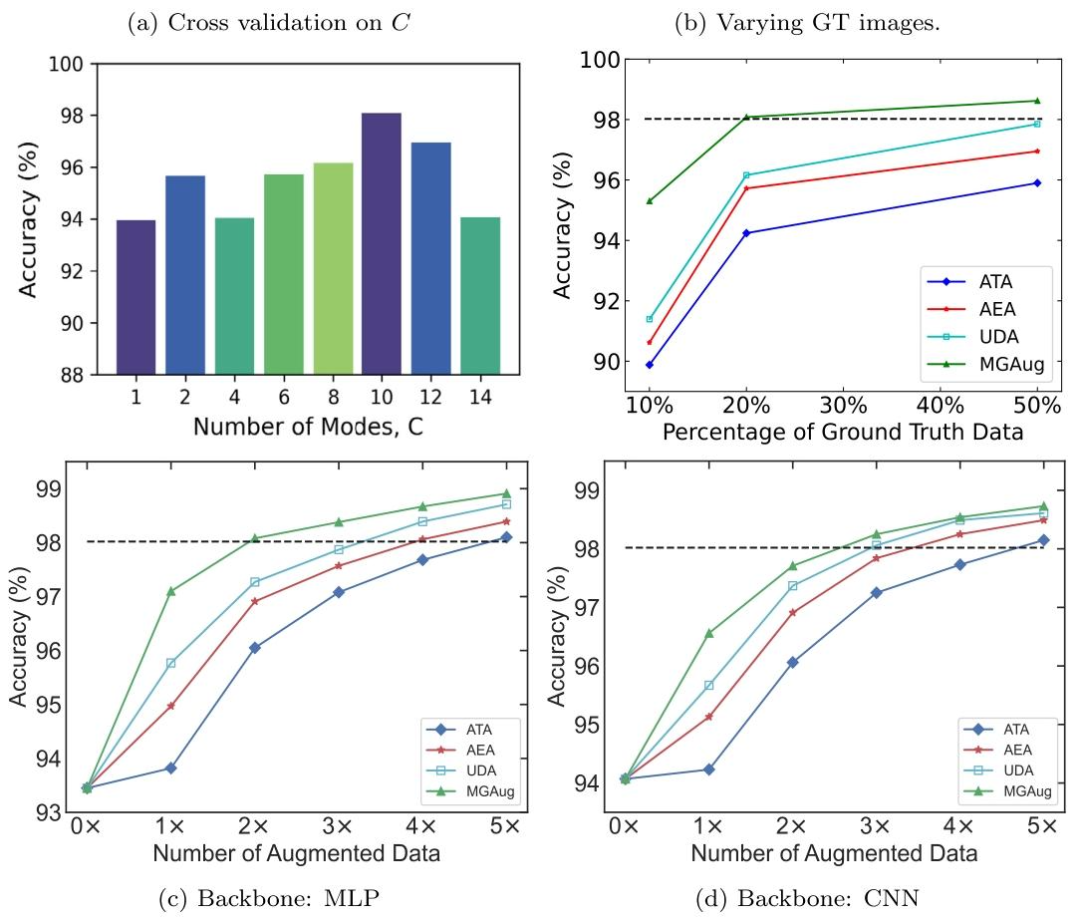
Fig. 5. Top: Accuracy comparison on various modes 𝐶 on 2D handwritten dataset taking 20% ground-truth images over 3× augmentations (left panel) and classification evaluationover increasing ground-truth images taking 3× augmentations (right panel). Bottom: A comparison of classification performance for all models on 2D handwritten digits overan increasing amount of augmented data taking 10% ground truth images under MLP (left panel) and CNN backbone (right panel). The horizontal dashed line (- -) serves as areference, representing the classification accuracy achieved when utilizing all available training images without any augmentation.

图5. 上图：使用20%真实标注图像并进行3倍增强时，2D手写数字数据集上不同模式数𝐶的准确率对比（左图），以及在3倍增强下随真实标注图像数量增加的分类性能评估（右图）。   下图：在MLP（左图）和CNN主干网络下，使用10%真实标注图像时，各模型在2D手写数字数据集上随增强数据量增加的分类性能对比。水平虚线（- -）作为参考，表示不使用任何增强、利用所有可用训练图像时的分类准确率。

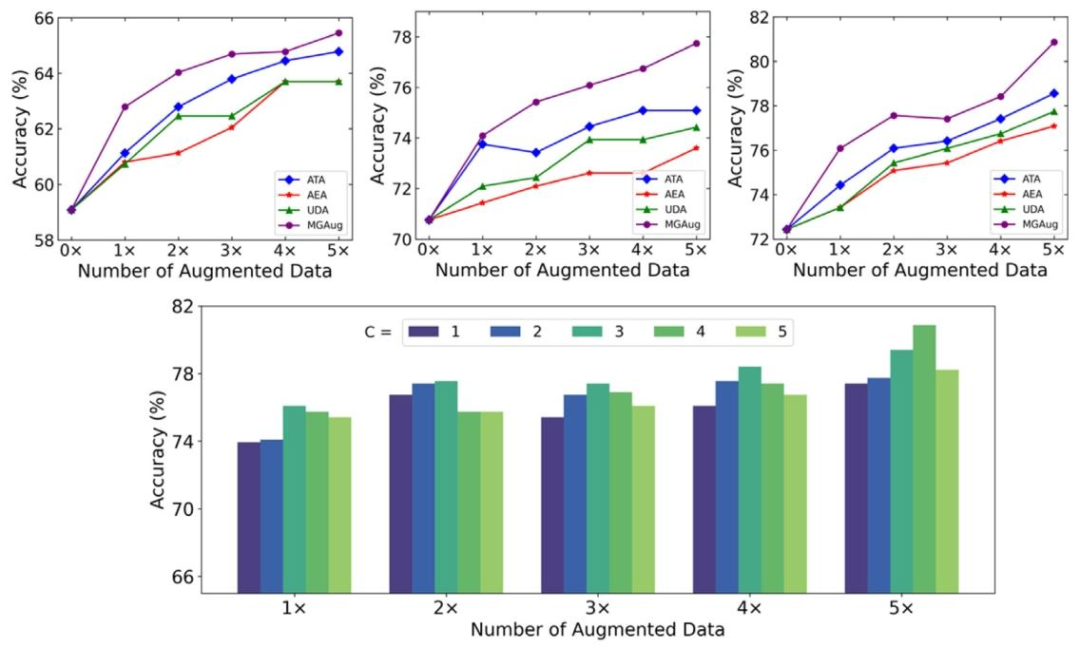
Fig. 6. Top: A comparison of classification performance for all models over increasing number of augmented data taking 25% (top-left), 50% (top-middle), and 75% (top-right)ground truth images. Bottom: Accuracy comparison on various modes C on 3D brain MRI dataset for classification tasks.

图6. 上图：使用25%（左上）、50%（中上）和75%（右上）真实标注图像时，各模型在增强数据量增加情况下的分类性能对比。   下图：3D脑MRI数据集分类任务中，不同模式数𝐶的准确率对比。

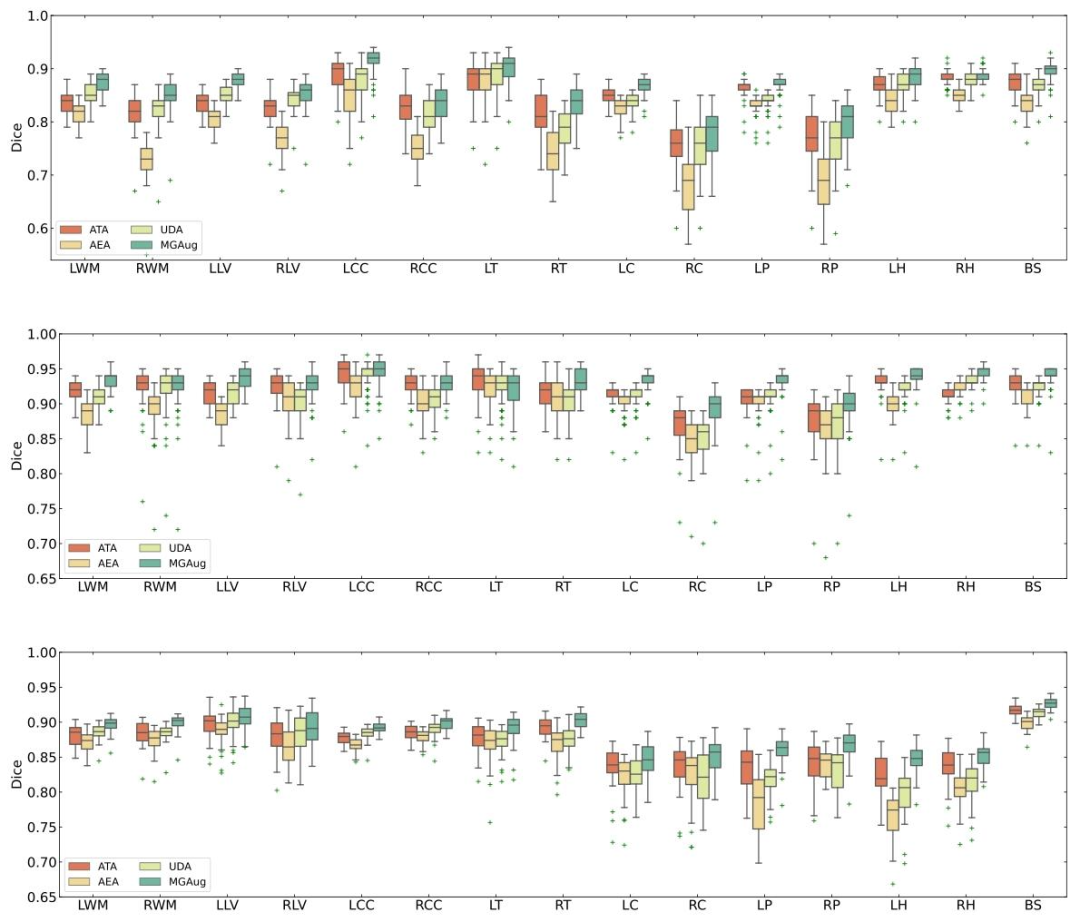
Fig. 7. Dice score comparison over fifteen anatomical brain structures (LWM - Left White Matter, RWM - Right White Matter, LLV - Left Lateral Ventricle, RLV - Right LateralVentricle, LCC - Left Cerebellum Cortex, RCC - Right Cerebellum Cortex, LT - Left Thalamus, RT - Right Thalamus, LC - Left Cudate, RC - Right Caudate, LP - Left Putamen, RP -Right Putamen, LH - Left Hippocampus, RH - Right Hippocampus, BS - Brain Stem) for four augmentation methods on 3× augmentations under UNet (top), UNetR (middle), andTransUNet (bottom) backbone. For fair comparison, we use 10%∕20%∕30% ground-truth images for UNet/UNetR/TransUNet backbones, respectively

图7：在UNet（上）、UNetR（中）和TransUNet（下）主干网络下，四种增强方法对15个脑部解剖结构（LWM - 左白质，RWM - 右白质，LLV - 左侧脑室，RLV - 右侧脑室，LCC - 左小脑皮层，RCC - 右小脑皮层，LT - 左丘脑，RT - 右丘脑，LC - 左尾状核，RC - 右尾状核，LP - 左壳核，RP - 右壳核，LH - 左海马，RH - 右海马，BS - 脑干）进行3倍增强后的Dice分数对比。为公平比较，UNet/UNetR/TransUNet主干网络分别使用10%/20%/30%的真实标注图像。

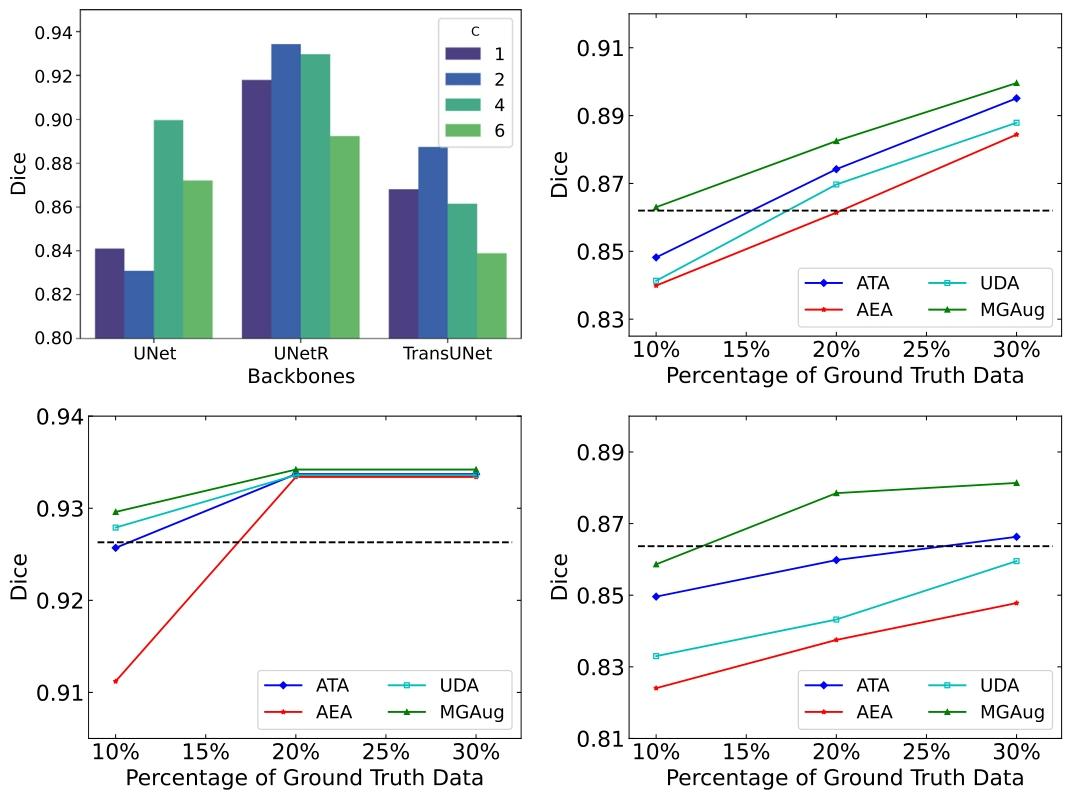
Fig. 8. Top-Left: Dice comparison on various modes 𝐶 on 3D brain MRI dataset. Right: A comparison of segmentation performance for all models over increasing number ofground-truth data (10% – 30%) under UNet (Top-Right), UNetR (Bottom-Left), and TransUNet (Bottom-Right) backbones. For fair comparison, we augment the data 3× to theground truth images. The horizontal dashed line (- -) serves as a reference, representing the segmentation dice score achieved when utilizing all available training images withoutany augmentation.

图8   左上：3D脑MRI数据集上不同模式数𝐶的Dice分数对比。   右侧：在UNet（右上）、UNetR（左下）和TransUNet（右下）主干网络下，所有模型随真实标注数据量（10%–30%）增加的分割性能对比。为公平比较，我们将真实标注图像增强3倍。水平虚线（- -）作为参考，表示不使用任何增强、利用所有可用训练图像时的分割Dice分数。

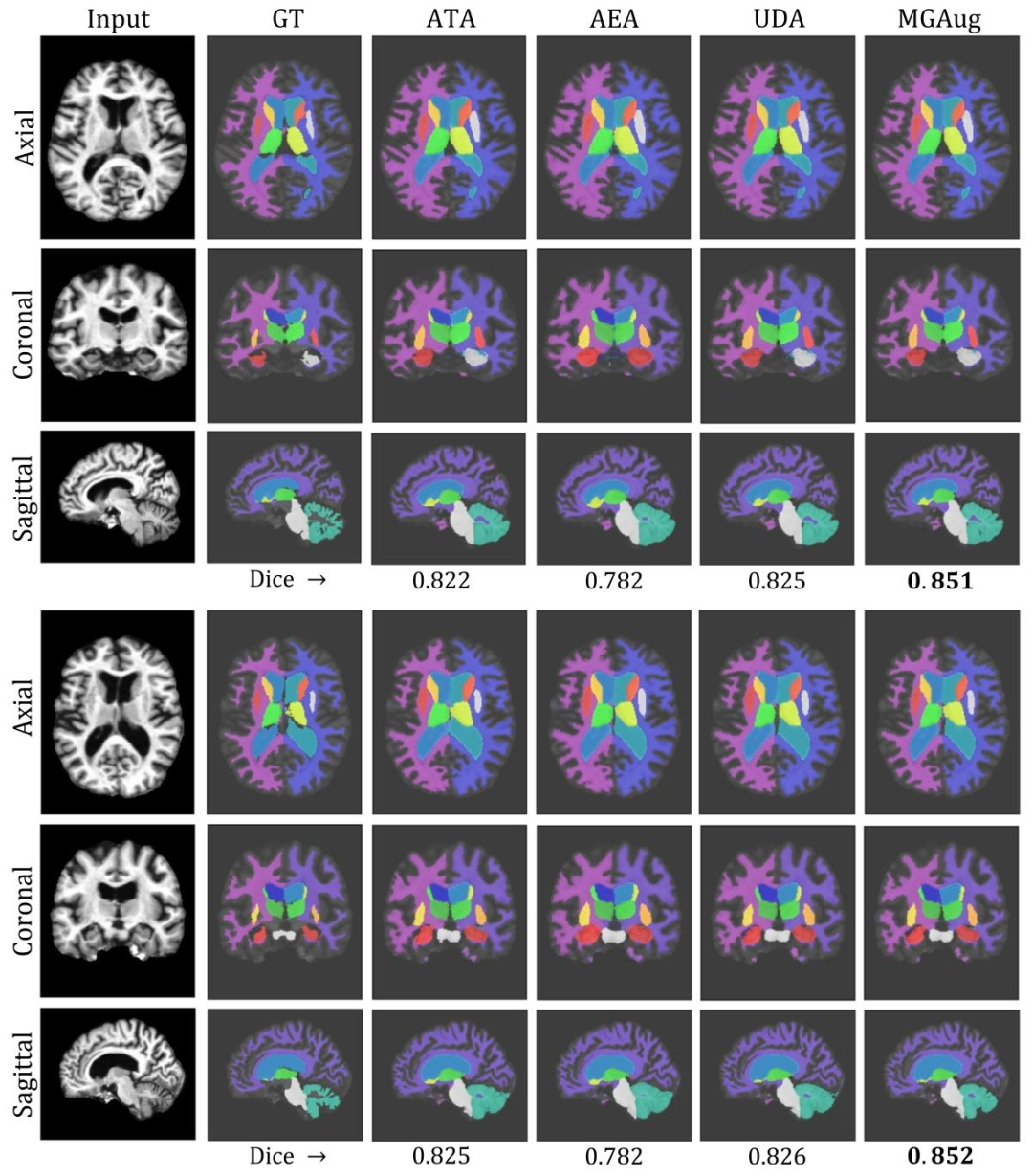
Fig. 9. Left to Right: Examples of segmentation (overlaid with input images) comparisons between the ground truth (GT) and predictions of all baselines including MGAug on 3Dbrain MRIs over three anatomical views (Top to Bottom: Axial, Coronal, and Sagittal)

图9 从左到右：在3D脑MRI的三个解剖视图（从上到下：轴位、冠状位、矢状位）上，真实标注（GT）与包括MGAug在内的所有基线模型预测的分割结果（叠加在输入图像上）对比示例。

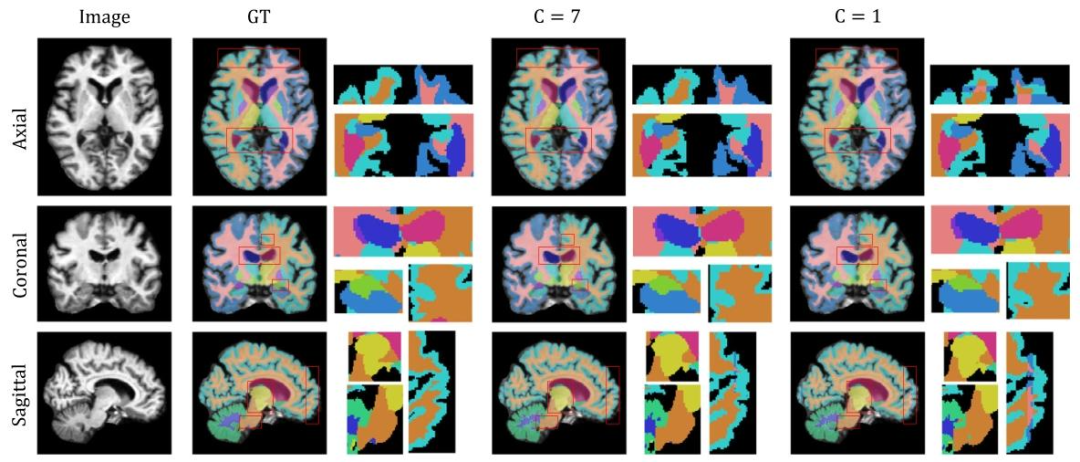
Fig. 10. Left to Right: Segmentation comparisons between ground truth (GT), multimodal (𝐶 = 7) and unimodal (𝐶 = 1) MGAug with a zoomed-in view, over three anatomicalviews (Top to Bottom: Axial, Coronal, and Sagittal).

图10 从左到右：真实标注（GT）、多模态（𝐶=7）和单模态（𝐶=1）MGAug的分割结果对比（含放大视图），展示三个解剖视图（从上到下：轴位、冠状位、矢状位）。

Table

表

Table 1Accuracy comparison on synthetic 2D shapes over all models with various network backbones

表1 基于不同网络主干的所有模型在合成2D形状上的准确率对比

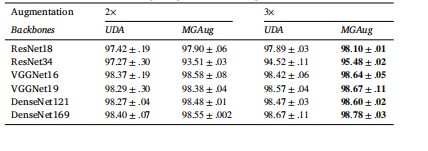
Table 2Accuracy comparison on 2D handwritten digits over unimodal UDA model acrossvarious network backbones using 2% ground truth images.

表2 基于单峰UDA模型在不同网络主干上使用2%真实标注图像的2D手写数字准确率对比

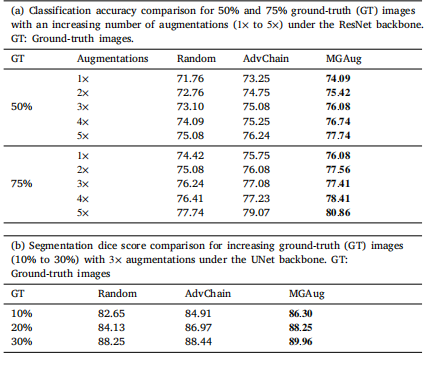
Table 3Performance comparison of random deformable augmentation (Random), adversarialdeformable augmentation (AdvChain), and MGAug on (a) multi-class classification and(b) segmentation dice on 3D brain MRI dataset.

表 3 随机可变形增强（Random）、对抗可变形增强（AdvChain）与 MGAug 在 3D 脑 MRI 数据集上的性能对比：(a) 多分类任务准确率；(b) 分割任务 Dice 分数

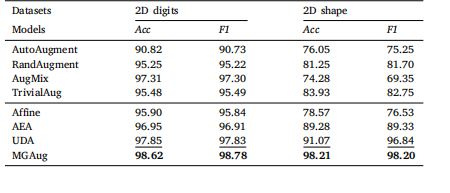
Table 4Accuracy comparison on both 2D digits and 2D shape datasets over a mix ofaugmentation methods (including intensity-based vs. transformation-based DA) on ViTbackbone.

表 4 在 ViT 主干网络上，混合增强方法（包括基于强度和基于变换的 DA）在 2D 数字和 2D 形状数据集上的准确率对比

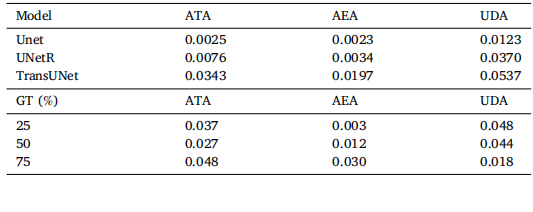
Table 5Statistical test of MGAug: (Left) p-values from paired student’s t-tests comparing MGAugwith baseline methods performing segmentation on 3D brain MRIs under differentsegmentation backbones; (Right) P-values for different ground truth percentages performing classification on 3D brain MRIs.

表 5 MGAug 的统计检验：（左）不同分割主干网络下，MGAug 与基线方法在 3D 脑 MRI 分割任务中配对学生 t 检验的 p 值；（右）3D 脑 MRI 分类任务中不同真实标注比例下的 p 值