当前位置：首页 > backend >正文

【卷积神经网络详解与实例】2——卷积计算详解

backend 2025/8/24 21:52:05

CNN中的卷积操作可以看做是输入和卷积核的内积运算。计算方法：一句话——对应元素相乘后求和再加上偏置项。

2.1 举例说明

2.1.1 简单例子

为了方便直接解释，我们首先以一个通道（若是彩图，则有RGB的颜色，所以是三个通道）为例进行讲解，首先明确概念：

输入是一个5*5的图片，其像素值如下：

$\begin{bmatrix} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ \end{bmatrix}$
卷积核（kernel）是需要训练的参数，这里为了讲解卷积运算的操作，所以最开始我们假设卷积核的值如下：

$\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \\ \end{bmatrix}$
通过窗口和卷积核的内积操作得到的结果叫做feature map。则卷积计算的过程如图所示：

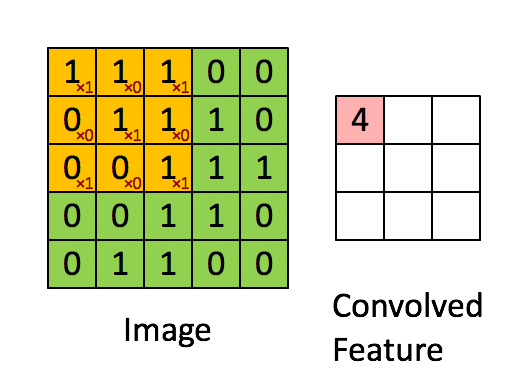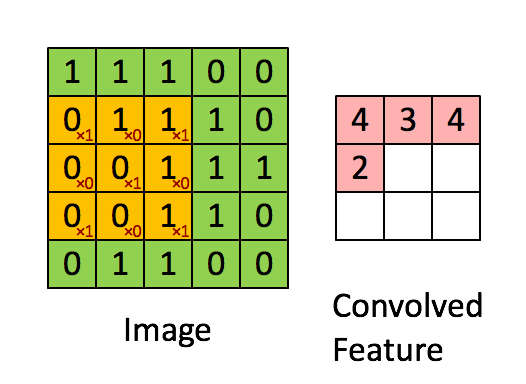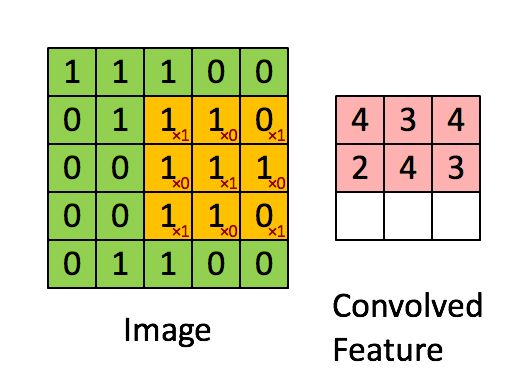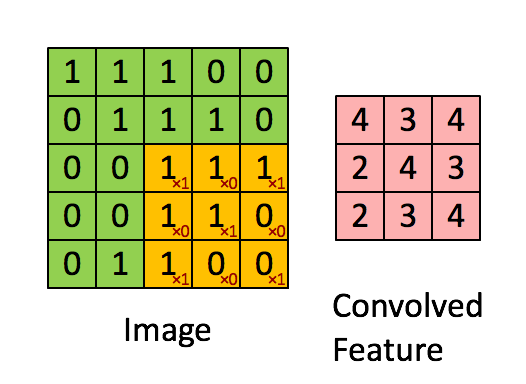
2.1.2 多个通道

若输入含有多个通道，则对于某个卷积核，分别对每个通道求feature map后将对应位置相加得到最终的feature map，如下图所示：

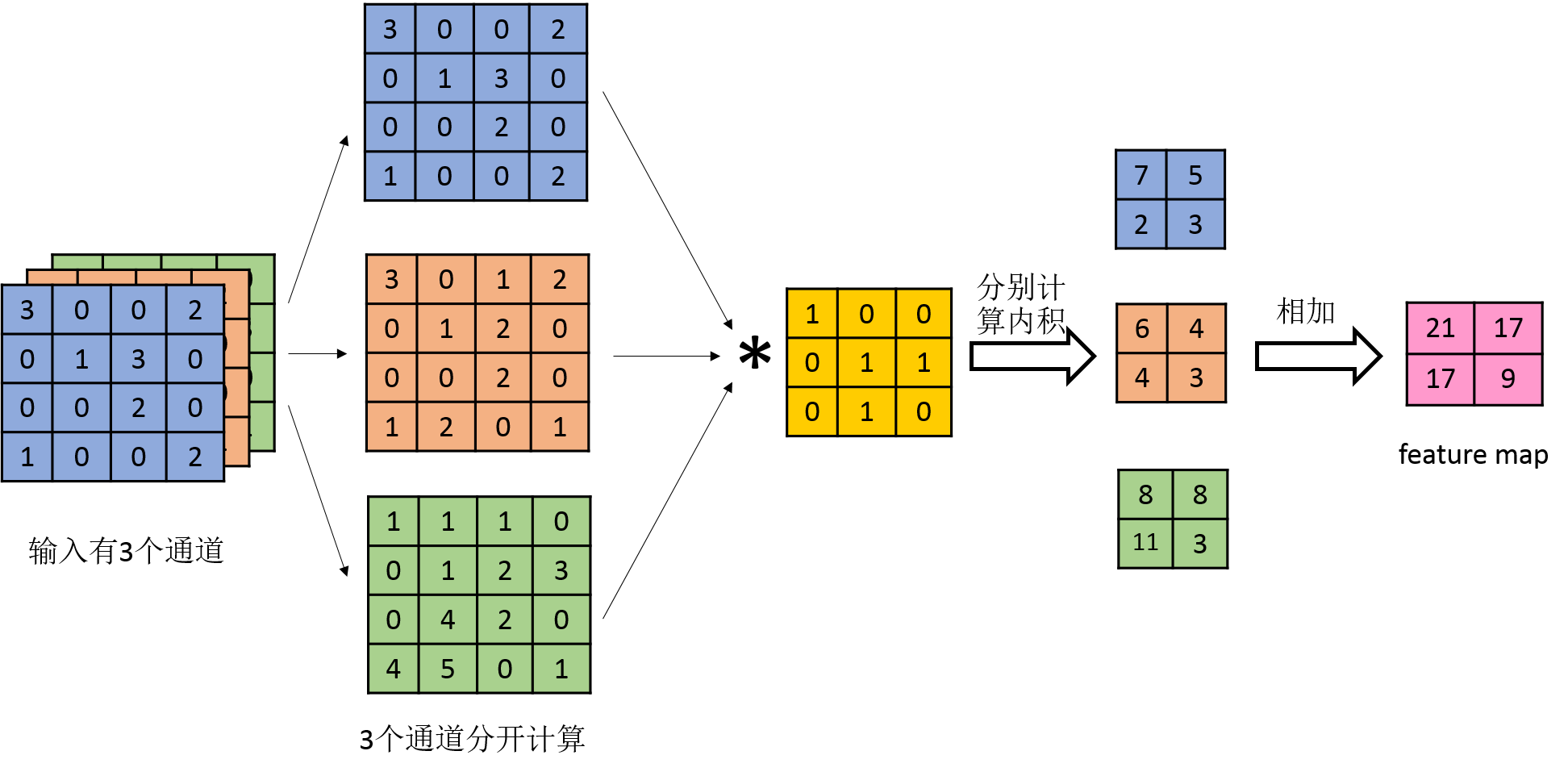
2.1.3 多个卷积核

若有多个卷积核，则对应多个feature map，也就是下一个输入层有多个通道。如下图所示：

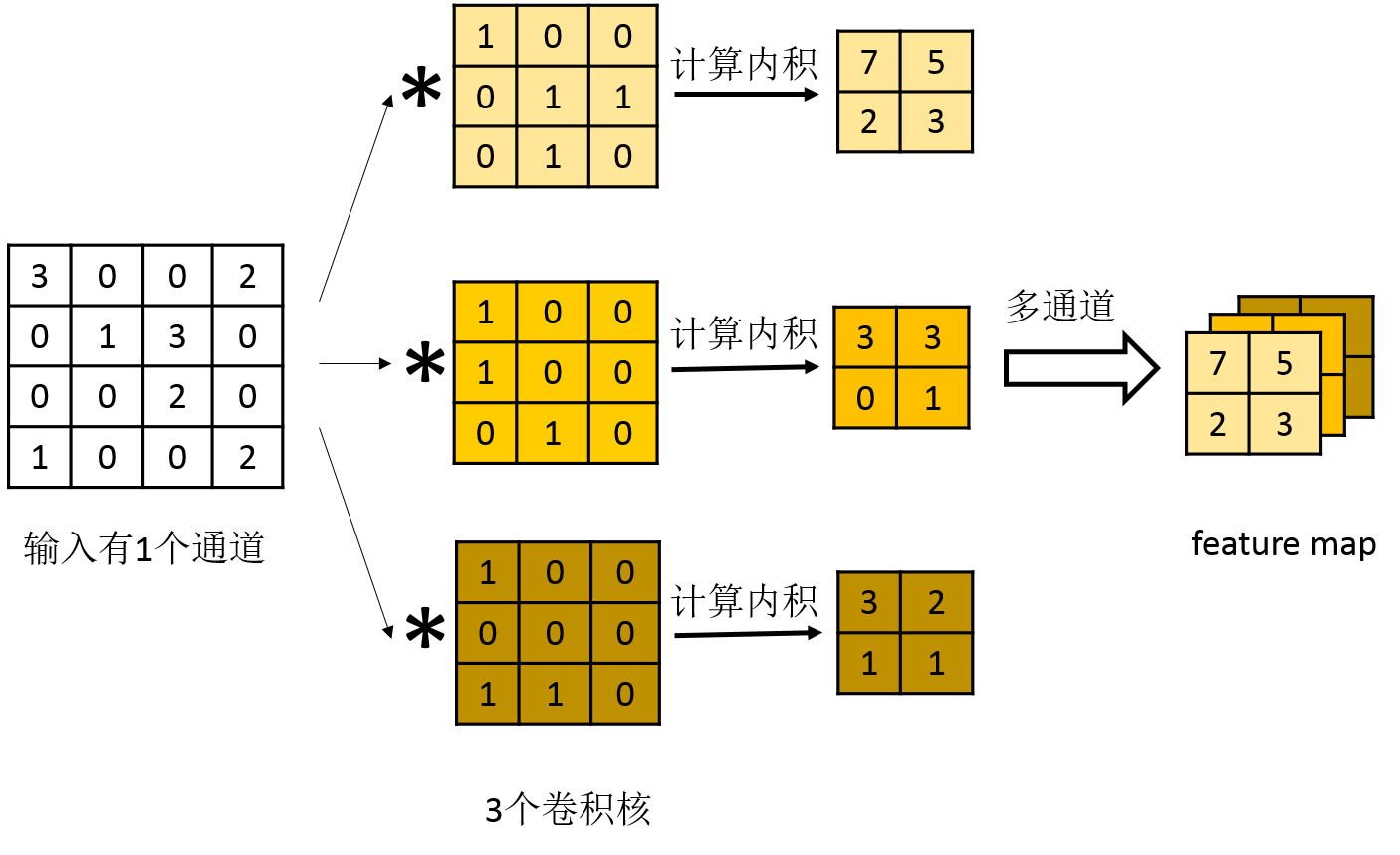
2.1.4 步长的解释

上述展示的步长（stride）为1的情况，若步长为2，则滑动窗口每2步产生一个，如下图所示：

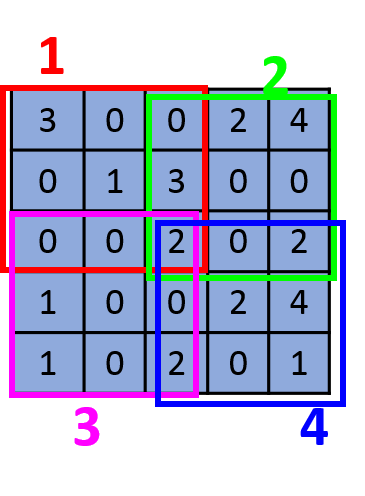
输入大小为 5 ∗ 5，卷积核的大小为 3 ∗ 3，最后的feature map的大小为 2 ∗ 2。

若假设输入大小是 $n \times n$ ，卷积核的大小是 $f \times f$ ，步长是 $s$ ，则最后的feature map的大小为 $o \times o$ ，其中 o 如下：

$o = \left\lfloor \frac{n - f}{s} \right\rfloor + 1$

2.1.5 详细例子：

Convolution Demo. Below is a running demo of a CONV layer. Since 3D volumes are hard to visualize, all the volumes (the input volume (in blue), the weight volumes (in red), the output volume (in green)) are visualized with each depth slice stacked in rows. The input volume is of size W1=5,H1=5,D1=3, and the CONV layer parameters are K=2,F=3,S=2,P=1. That is, we have two filters of size 3×3, and they are applied with a stride of 2. Therefore, the output volume size has spatial size (5 - 3 + 2)/2 + 1 = 3. Moreover, notice that a padding of P=1 is applied to the input volume, making the outer border of the input volume zero. The visualization below iterates over the output activations (green), and shows that each element is computed by elementwise multiplying the highlighted input (blue) with the filter (red), summing it up, and then offsetting the result by the bias.

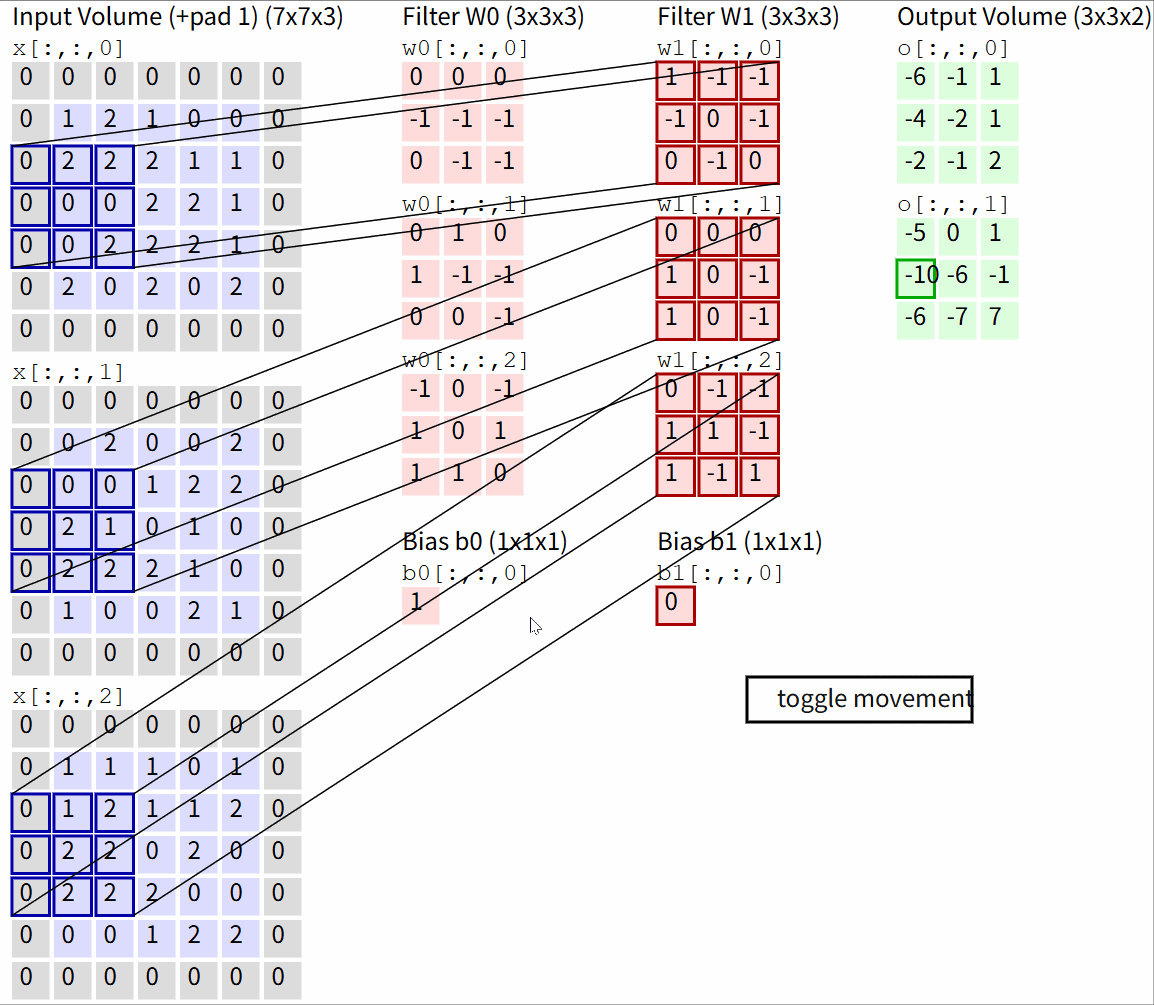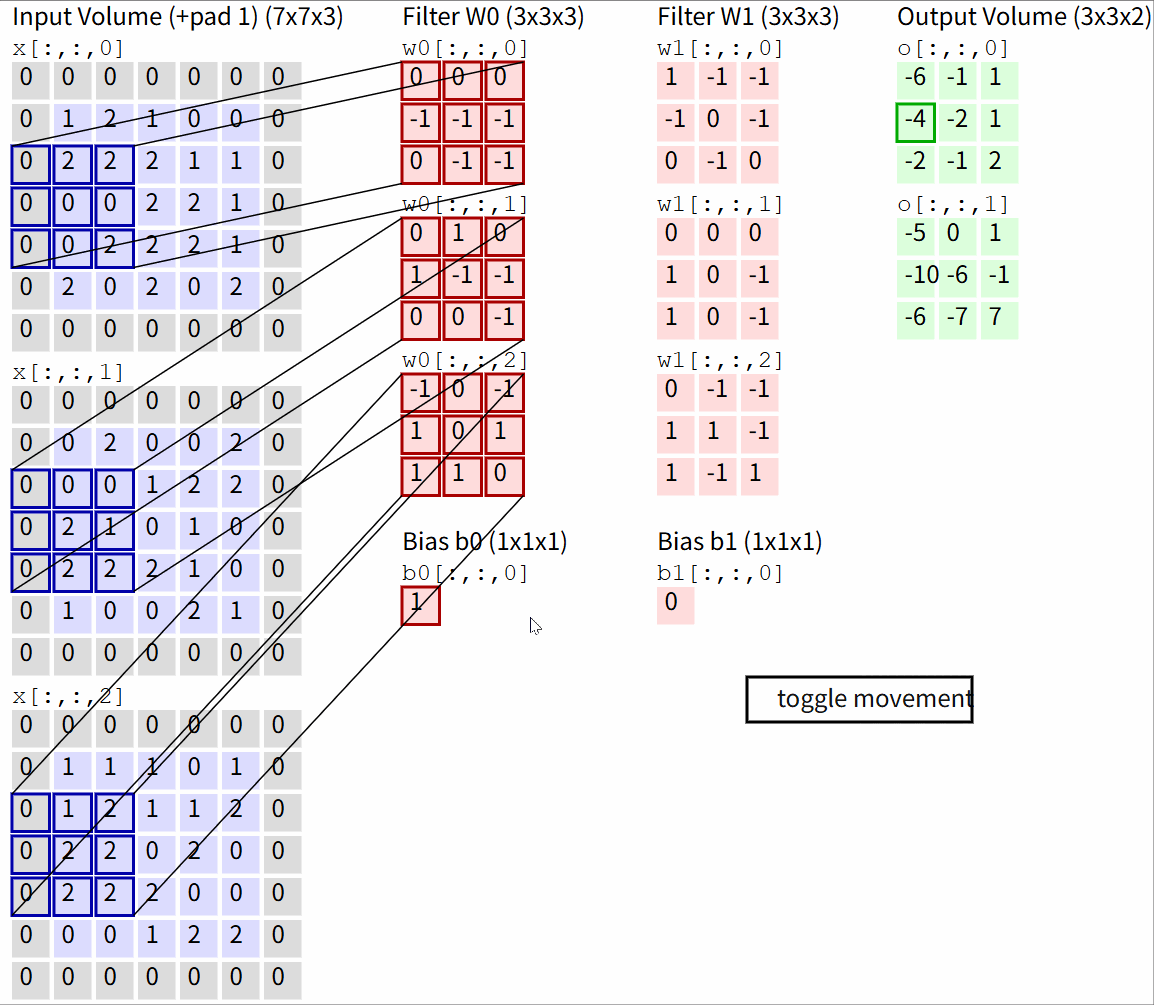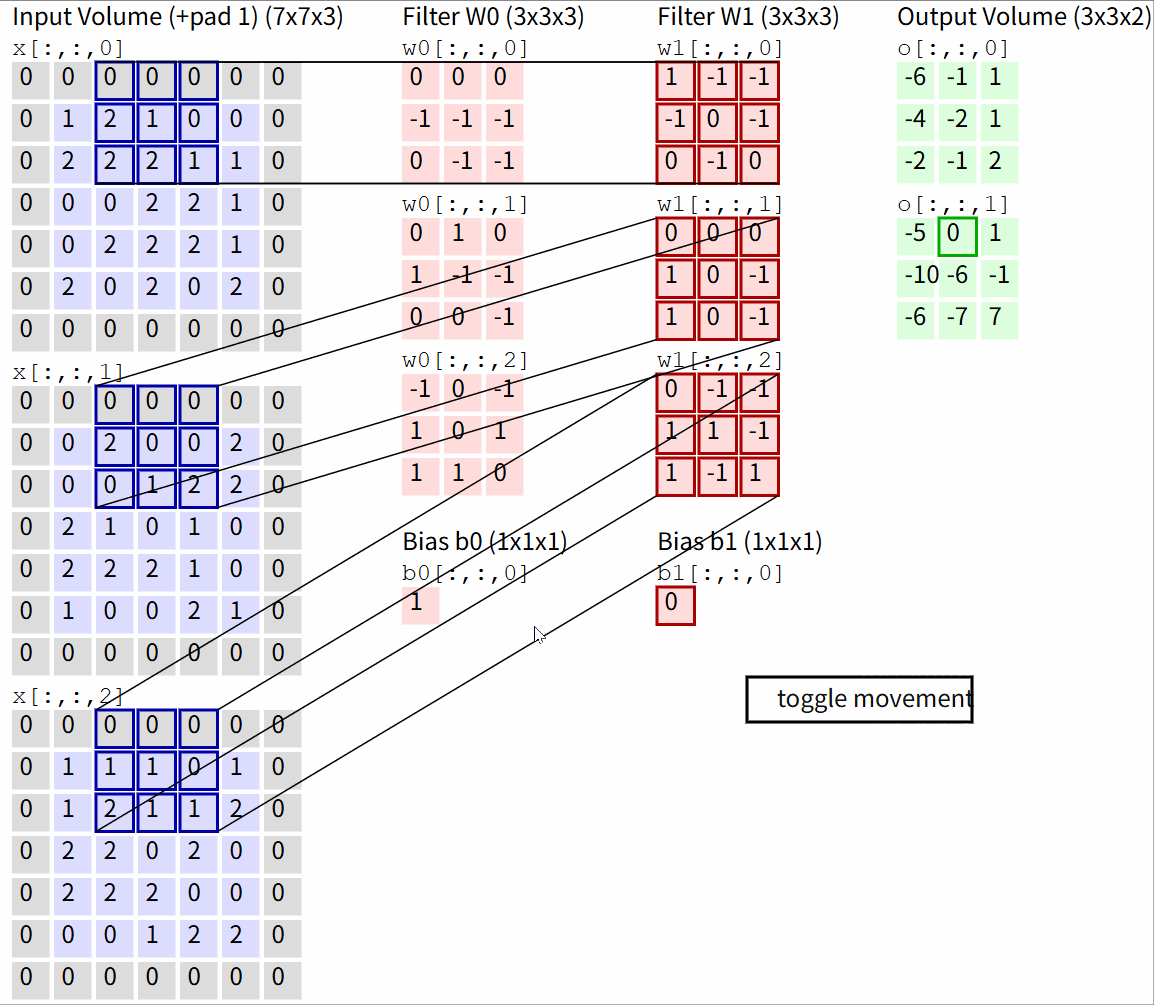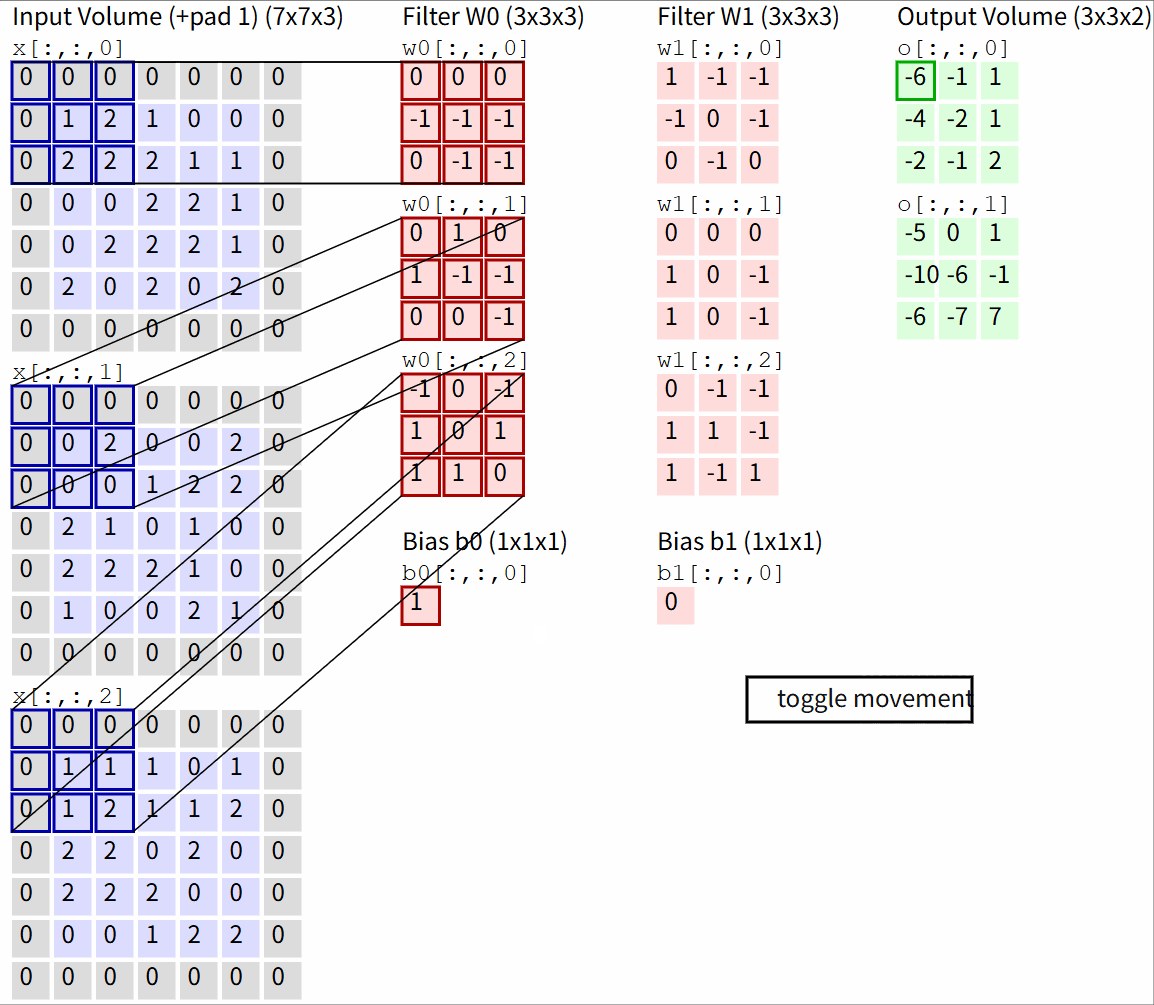
图源：CS231n Deep Learning for Computer Vision

2.2 三种卷积模式

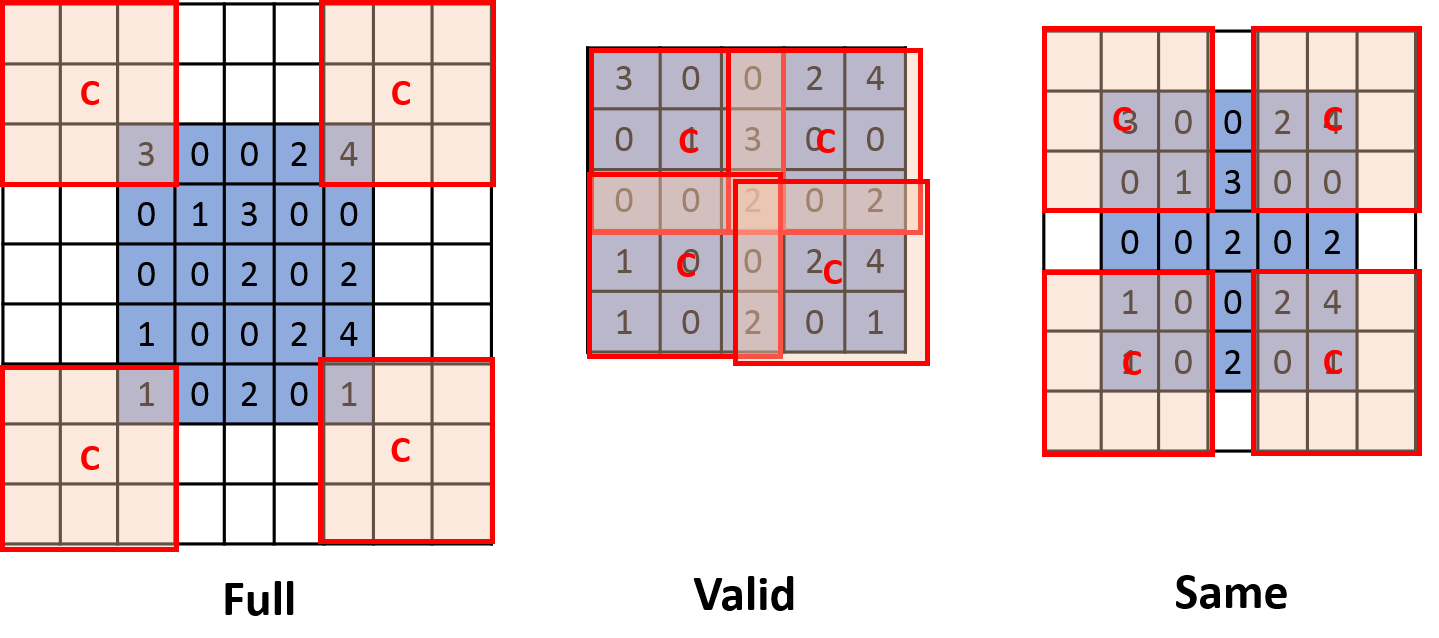
2.2.1 3种模式的区别

如上图所示，3种模式的主要区别是从哪部分边缘开始滑动窗口卷积操作：

Full模式：第一个窗口只包含1个输入的元素，即从卷积核（fileter）和输入刚相交开始做卷积。没有元素的部分做补0操作。
Valid模式：卷积核和输入完全相交开始做卷积，这种模式不需要补 0。
Same模式：当卷积核的中心 C 和输入开始相交时做卷积。没有元素的部分做补0操作。

在之前讲到的内容使用的是Valid的模式。

2.2.2 Full、Same和Valid下的feature map的大小

（1）若输入大小是 $n \times n$ ，卷积核大小为 $f \times f$ ，步长 (stride) 为 s ，若采用 Full 或 Same 模式，假设填充 (pad) 大小为 p （p为一边填充的大小，举例：如果输出 $5 \times 5$ ，卷积核 $3 \times 3$ ，采用 Full 模式，则 $p = 2$ ），则 feature map 的大小是：

$\left( \left\lfloor \frac{n + 2p - f}{s} \right\rfloor + 1 \right) \times \left( \left\lfloor \frac{n + 2p - f}{s} \right\rfloor + 1 \right)$

（2）若输入大小是 $n \times n$ ，卷积核大小为 $f \times f$ ，步长为 s ，若不补 0，即 Valid 模式下，feature map的大小为：

$\left( \left\lfloor \frac{n - f}{s} \right\rfloor + 1 \right) \times \left( \left\lfloor \frac{n - f}{s} \right\rfloor + 1 \right)$

（3）Same模式下，feature map的维度和输入维度相同。

注意：卷积核大小一般为奇数，原因如下：

当卷积核为偶数时，p不为整数，假设是Same模式，若想使得卷积之后的维度和卷积之前的维度相同，则需要对图像进行不对称填充，较复杂。

当kernel为奇数维时，有中心像素点，便于定位卷积核。

2.3 卷积的特点

局部视野

卷积操作在运算的过程中，一次只考虑一个窗口的大小，因此其具有局部视野的特点，局部性主要体现在窗口的卷积核的大小。
参数减少

比如，在上述输入为 $5 \times 5$ ，卷积核为 $3 \times 3$ （在ANN中，这相当于全连接层的权重矩阵），输出为 $3 \times 3$ 的例子中，如果是使用 ANN，则其参数个数为 $(5 \times 5) \times (3 \times 3)$ 。而在CNN中，其参数个数为卷积核的大小 $3 \times 3$ 。

这只是简单的情况，若输入非常大，卷积核通常不是很大，此时参数量的差距将会非常明显。
权重共享

从上面的讲解可以看到，对一个输入为 $5 \times 5$ ，卷积核为 $3 \times 3$ 的情况下，对于每一个滑动窗口，使用的都是同一个卷积核，所以其参数共享。