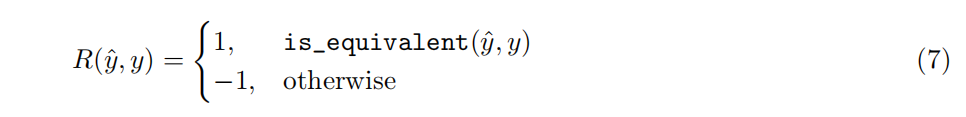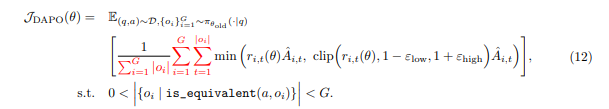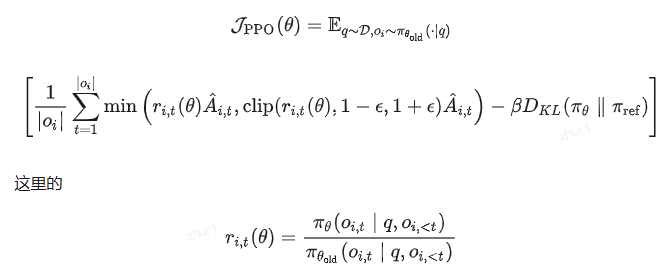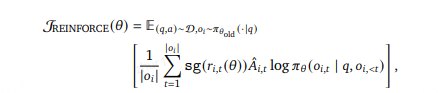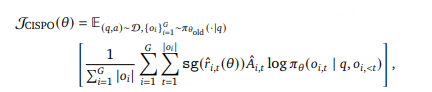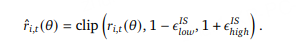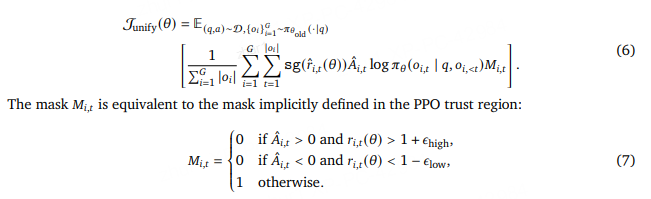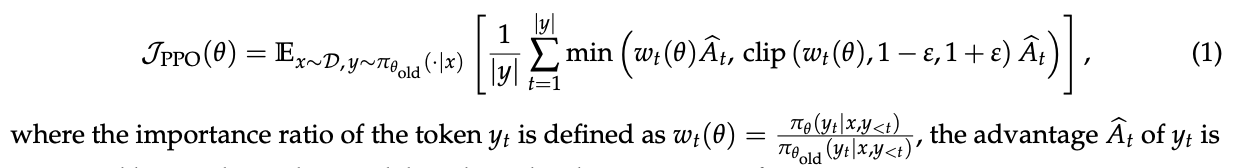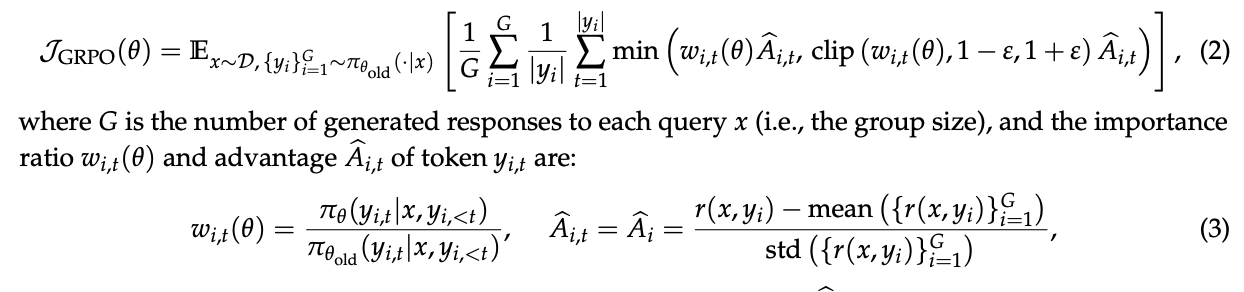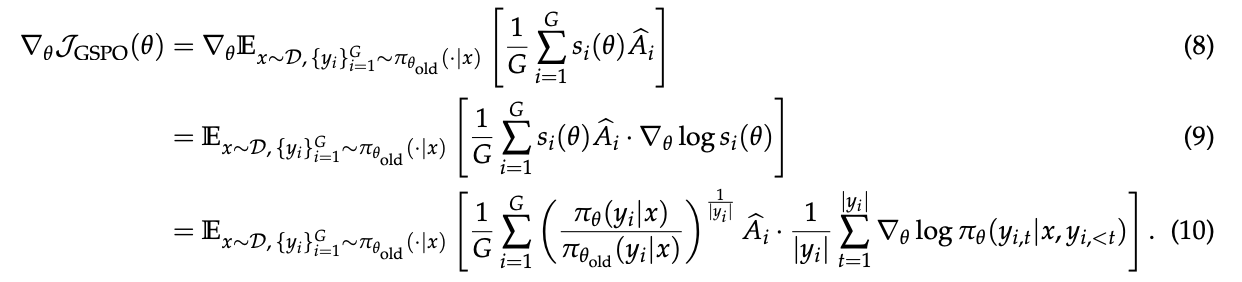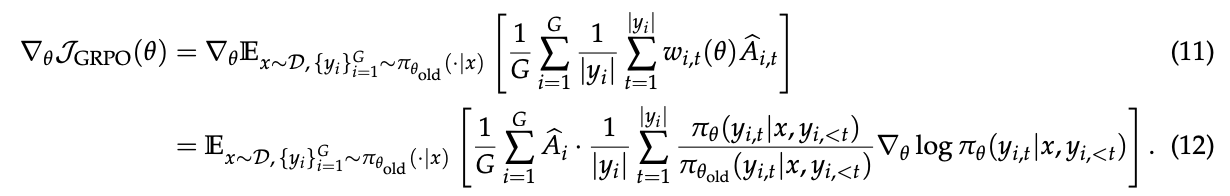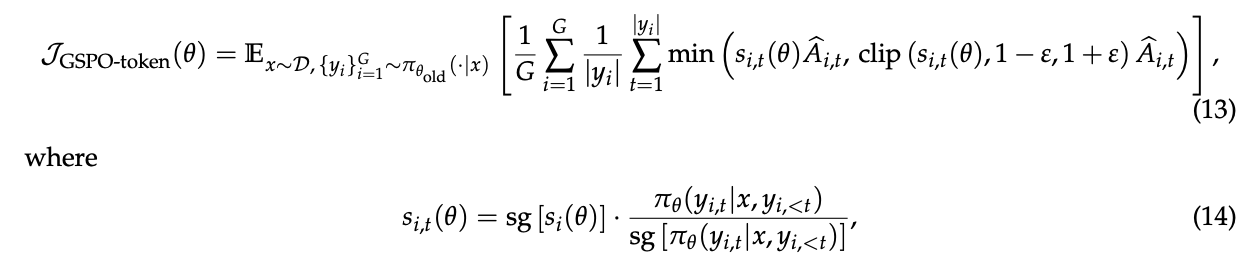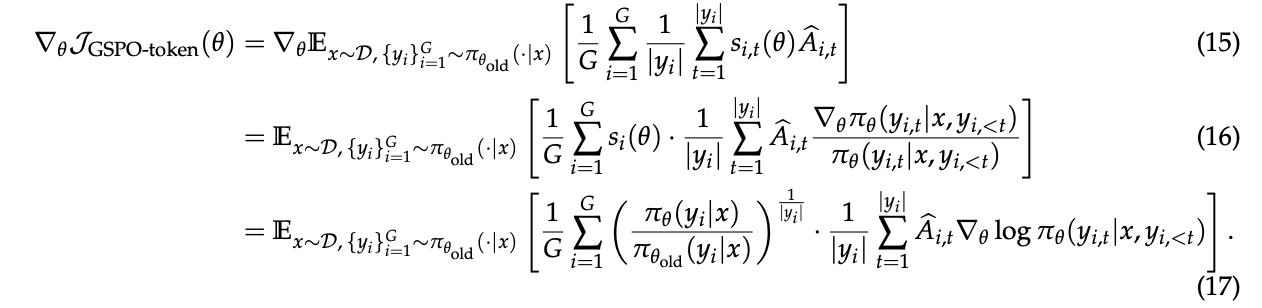强化学习进化之路(GRPO-＞DAPO-＞Dr.GRPO-＞CISPO-＞GSPO)

PPO:
Remax:从多个生成样本中选择reward最高的那个,仅针对最优样本更新模型,类似"优胜劣汰"
RLOO:对于同一 prompt 在线采样k次，取除自己外的其他k-1条回答的平均 reward 作为 baseline。
DPO:不需要奖励模型，一对数据学习
KTO:一个数据，只要告诉我这个回答是不是所期望的就行
ODPO:不会平等对待每个偏好对
ORPO:加入优势比，拉远正负样本的距离
simPO:解决了DPO训练和推理目标没有完全对齐的问题，去除了ref model的loss，增加长度归一化让模型生成更短的回答
强化学习进化之路(PPO-＞ReMax&RLOO-＞DPO-＞KTO-＞ODPO-＞ORPO-＞simPO)
如利用历史重采样的 SRPO、采用动态采样的 DAPO

GRPO:组
REINFORCE++：Token 级别的 KL 惩罚；小批量更新提高稳定性和效率；奖励归一化与截断增强稳定性避免爆炸；优势归一化
DAPO：移除KL散度，提高clip上限。Clip-Higher策略、动态采样、Token级梯度优化、智能长度惩罚
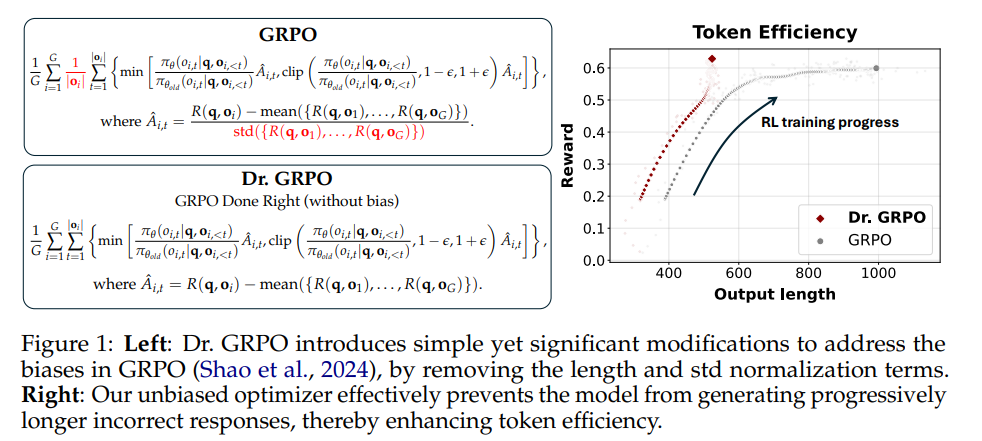
Dr.GRPO：从 GRPO 公式中删除了有问题的长度和奖励归一化项。具体来说，它消除了导致模型更新不平衡的响应长度和标准差缩放因子。修改后的算法可以更公平地计算不同响应和问题类型的梯度。
CISPO：token裁剪按照重要性采样
GSPO:将重要性比例的定义从“词元级别”提升到了“序列级别”

三 GRPO

GRPO 是一种在线学习算法（online learning algorithm），这意味着它通过使用训练过程中由训练模型自身生成的数据来迭代改进。GRPO 的目标直觉是最大化生成补全（completions）的优势函数（advantage），同时确保模型保持在参考策略（reference policy）附近。

为了理解 GRPO 的工作原理，可以将其分解为四个主要步骤：
生成补全（Generating completions）
计算优势值（Computing the advantage）
估计KL散度（Estimating the KL divergence）
计算损失（Computing the loss）

3.1. 生成补全（Generating completions）

在每一个训练步骤中，我们从提示（prompts）中采样一个批次（batch），并为每个提示生成一组 G个补全（completions）（记为 oi o_i o_i ）。

3.2. 计算优势值（Computing the advantage）

对于每一个 G序列，使用奖励模型（reward model）计算其奖励（reward）。
为了与奖励模型的比较性质保持一致——通常奖励模型是基于同一问题的输出之间的比较数据集进行训练的——优势的计算反映了这些相对比较。
其归一化公式如下：A

这种方法赋予了该方法其名称：群体相对策略优化（Group Relative Policy Optimization, GRPO）

GRPO通过优化PPO算法，解决了计算优势值时需要同时依赖奖励模型（reward model）和价值模型（value model）的问题，成功移除了value model（价值模型），显著降低了推理时的内存占用和时间开销。Advantage（优势值）的核心价值在于为模型输出提供更精准的评估，不仅衡量答案的绝对质量，还通过相对比较（与其他回答的对比）来更全面地定位其优劣。

3.3. 估计KL散度（Estimating the KL divergence）

在实际算法实现中，直接计算KL散度可能会面临一些挑战：

• 计算复杂度高：KL散度的定义涉及对两个概率分布的对数比值的期望计算。对于复杂的策略分布，直接计算KL散度可能需要大量的计算资源；
• 数值稳定性：在实际计算中，直接计算KL散度可能会遇到数值不稳定的问题，尤其是当两个策略的概率分布非常接近时，对数比值可能会趋近于零或无穷大。近似器可以通过引入一些数值稳定性的技巧（如截断或平滑）来避免这些问题；
• 在线学习：在强化学习中，策略通常需要在每一步或每几步更新一次。如果每次更新都需要精确计算KL散度，可能会导致训练过程变得非常缓慢。近似器可以快速估计KL散度，从而支持在线学习和实时更新。

Schulman et al. (2020) Approximating KL Divergence
提出的近似器可以根据当前策略和参考策略的差异动态调整估计的精度，从而在保证计算效率的同时，尽可能减少估计误差，其定义如下

这个近似器的核心思想是通过对当前策略和参考策略的概率比值的简单变换来估计KL散度。
具体来说：

这个近似器的优势在于它只需要计算当前策略和参考策略的概率比值，而不需要直接计算KL散度的积分或期望。因此，它可以在保证一定精度的同时，显著降低计算复杂度。

近似器的直观理解
这个近似器的设计灵感来自于泰勒展开。KL散度可以看作是两个分布之间的某种“距离”，而这个近似器通过一阶或二阶近似来估计这个距离。具体来说：
当兀与兀ref非常接近时，log(兀/兀ref)近似器的值趋近于零，符合KL散度的性质。
当兀与兀ref差异较大时，近似器会给出一个较大的正值，反映出两个分布之间的差异。

3.4. 计算损失（Computing the loss）

这一步的目标是最大化优势，同时确保模型保持在参考策略附近。因此，损失定义如下：

其中第一项表示缩放后的优势，
第二项通过KL散度惩罚与参考策略的偏离。

在原始论文中，该公式被推广为在每次生成后通过利用裁剪替代目标（clipped surrogate objective）进行多次更新：

其中 clip(⋅,1−ϵ,1+ϵ) 通过将策略比率限制在 1−ϵ 和 1+ϵ 之间，确保更新不会过度偏离参考策略。

在很多代码实现，比如Huggingface的TRL中，与原始论文一样每次生成只进行一次更新，因此可以将损失简化为第一种形式。

3.5 总结

GRPO通过优化PPO算法，移除了价值模型，降低了计算开销，同时利用群体相对优势函数和KL散度惩罚，确保策略更新既高效又稳定。

想象一下，你是个销售员，这个月业绩10万块，
PPO算法就像个精明的老会计，拿着算盘噼里啪啦一顿算，考虑市场行情、产品类型，最后得出结论：“嗯，这10万还算靠谱，但GAE一算，发现你的优势值还不够高，还得再加把劲啊”
而GRPO呢，就像老板直接搞了个“内卷大赛”，把所有销售员拉到一个群里，每天晒业绩：“你10万，他15万，她20万……”老板还时不时发个红包，刺激大家继续卷。你的10万块在群里瞬间被淹没，老板摇摇头：“你这水平，还得加把劲啊！”
GRPO这招绝了，它把PPO的“算盘”扔了，省了不少计算功夫，直接搞“内卷PK”，用KL散度惩罚来确保大家别躺平。这样一来，策略更新既快又稳，老板再也不用担心有人摸鱼了，毕竟大家都在拼命卷，谁敢松懈？

总结一下：
PPO是“单打独斗看实力”，
GRPO是“内卷大赛拼到死”，
最后GRPO还省了算盘钱，老板笑得合不拢嘴，而我们只能默默加班，继续卷。

GRPO的关键点一：分组采样与相对奖励
GRPO 中，“分组”非常关键

GRPO的核心思想是通过组内相对奖励来估计基线（baseline），从而避免使用额外的价值函数模型（critic model）。
传统的PPO算法需要训练一个价值函数来估计优势函数（advantage function），而GRPO通过从同一问题的多个输出中计算平均奖励来替代这一过程，显著减少了内存和计算资源的消耗。

1. 框架图

首先看一下PPO 与GRPO 的比较图。

从图上可以看出，GRPO 与PPO 的主要区别有：
GRPO 省略了 value function model.
GRPO reward 计算，改成了一个q 生成多个r, 然后reward 打分。
PPO 优势函数计算时，KL 是包含在GAE内部的。 GRPO 直接挪到了外面，同时修改了计算方法。

2. 算法原理

2.1 PPO 复习

直接上原文，首先是PPO 的目标函数：

这个比较熟悉，策略概率比与优势函数的乘积。 同时做了clip限制了参数更新范围。

公式2 是PPO 中优势函数的计算。 在reward 打分上，加一个per-token 的KL 散度惩罚。

2.2 GRPO的优化

由于 PPO 中使用的价值函数通常是与策略模型大小相当的另一个模型，因此会带来大量的内存和计算负担。此外，在强化学习（RL）训练期间，价值函数被视为计算优势以减少方差的基线。

然而，在大语言模型（LLM）的背景下，通常只有最后一个 Token 会被奖励模型赋予奖励分数，这可能会使在每个 Token 上都准确的价值函数的训练变得复杂。为了解决这个问题，我们提出了组相对策略优化（GRPO），它无需像 PPO 那样进行额外的价值函数近似，而是使用针对同一问题生成的多个采样输出的平均奖励作为基线。

去除value function , reward 直接对单个q生成的response进行打分，归一化后，作为替代的优势函数。

GRPO 利用组相对方式计算优势，与奖励模型的比较性质非常吻合，因为奖励模型通常在同一问题的输出比较数据集上进行训练。
另请注意，GRPO 不是在奖励中添加 KL 惩罚，而是通过直接将训练策略和参考策略之间的 KL 散度添加到损失中进行正则化，从而避免了Ait的计算复杂化。与PPO中使用的 KL 惩罚项不同，我们使用以下无偏估计器估计 KL 散度：将KL散度抑制，移到了优势函数计算的外面。可以见公式4. 为了保证KL散度为正值。

下图是基于group reward 计算优势函数的，归一化公式：

下面是GRPO 的计算伪代码：

GRPO的计算流程包括：

• 采样一组输出并计算每个输出的奖励。
• 对组内奖励进行归一化处理。
• 使用归一化后的奖励计算优势函数。
• 通过最大化目标函数更新策略模型。
• 迭代训练，逐步优化策略模型。

GRPO通过组内相对奖励估计基线，避免了传统PPO中价值函数的使用，显著减少了训练资源消耗，同时提升了模型在数学推理等复杂任务中的表现。

3. GRPO 计算总结

这里的公式缺了一部分，不要在意。可以查看查看原文截图。

GRPO 的确节约了显存和计算资源。 但是是否真的提升复杂任务能力保留疑问。

4. GRPO对比

4.1 为什么说GRPO中的概率比是重要性采样？

1. 重要性采样的基本概念：
   重要性采样是一种通过调整样本权重，用旧分布（旧策略）的样本来估计新分布（新策略）期望值的方法。其核心公式为：
   
2. GRPO中的重要性采样应用：
   
3. 与经典策略梯度方法的对比：
   传统策略梯度（如提到的Policy Gradient）直接通过蒙特卡洛采样估计梯度，但需要大量新策略的样本。而GRPO通过重要性采样，复用旧策略的样本来估计新策略的改进方向，显著降低了训练成本。

四 REINFORCE++

REINFORCE++ 的一个关键优势是，它比 GRPO 更加稳定，比 PPO 更加高效。

REINFORCE 是强化学习中一种重要且简单的策略梯度方法，旨在通过直接优化策略来最大化期望的累积奖励。该算法采用蒙特卡洛方法，按以下步骤执行：

4.1 REINFORCE++ 中的关键优化技巧

参考：

为了稳定模型训练，REINFORCE++ 中引入了多个优化技巧：

Token 级别的 KL 惩罚
Token 级别的 KL 惩罚的优势在于，它可以与过程奖励模型（PRM）无缝结合，实现信用分配，只需在奖励 Token 的位置添加 即可。最近，有研究者发现，在 REINFORCE++ 中与 GRPO 一起使用外部 KL 损失也能取得良好效果

小批量更新
小批量更新通过以下方式提高了训练效率和稳定性：将训练数据分成更小的批次，而不是使用整个数据集进行更新。允许每个小批次进行多个参数更新，从而加速收敛并减少内存消耗。引入随机性，帮助避免局部最优解，并提高模型的泛化能力。

奖励归一化与截断
该方法通过以下两种方式解决了奖励信号的波动性问题：
奖励归一化：对奖励进行标准化（例如，减去均值并除以标准差），使奖励信号更加平滑，增强训练的稳定性。
奖励截断：将奖励值限制在一定范围内，减少极端奖励对模型更新的影响，避免梯度爆炸。

优势归一化
优势归一化有助于管理 REINFORCE++ 中优势函数的方差。该优势函数的估计公式如下：

PPO-Clip

五 DAPO

字节跳动与清华大学联合推出的DAPO（Decoupled Clip and Dynamic sAmpling Policy Optimization）。

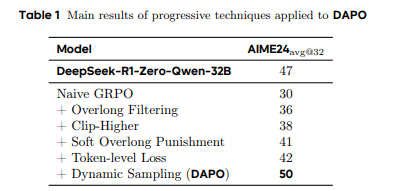
DAPO不仅以50分的惊人成绩刷新了数学竞赛AIME 2024的纪录（超越此前SOTA模型DeepSeek-R1的47分），更以完全开源的姿态，将算法、代码、数据集公之于众。更令人惊叹的是，DAPO仅用一半的训练步骤便达成这一里程碑，背后四大核心技术——Clip-Higher策略、动态采样、Token级梯度优化、智能长度惩罚——直指RL训练的痛点：熵崩溃、奖励噪声、长文本低效学习。

项目地址：https://dapo-sia.github.io/
数据：https://huggingface.co/datasets/BytedTsinghua-SIA/DAPO-Math-17k
代码：GitHub - BytedTsinghua-SIA/DAPO
论文：https://dapo-sia.github.io/static/pdf/dapo_paper.pdf

5.1 移除KL散度

在RLHF（人类反馈强化学习）场景中，KL散度用于限制在线策略与冻结参考策略之间的偏离。然而，在长链式推理模型的训练中，模型分布可能会显著偏离初始模型，因此这种限制并不必要。DAPO算法移除了KL散度项，从而允许模型在训练过程中自由探索。

5.2 基于规则的奖励建模

传统的奖励模型往往面临奖励黑客问题，即模型通过操纵奖励信号来获得高分，而非真正提升推理能力。DAPO直接使用可验证任务的最终准确率作为奖励，避免了奖励模型的复杂性。具体来说，奖励函数如下：

这种方法在自动定理证明、计算机编程和数学竞赛等多个领域被证明是有效的。

5.3 DAPO算法

DAPO算法的核心在于解耦裁剪和动态采样策略优化。DAPO通过以下目标函数优化策略：

DAPO的四大核心技术如下

5.3.1 提高上限：Clip-Higher

在初始实验中，研究人员发现PPO和GRPO算法存在熵崩溃现象，即策略的熵随着训练迅速下降，导致生成的响应趋于一致。
为了解决这一问题，DAPO提出了Clip-Higher策略，通过解耦上下裁剪范围，增加低概率token的探索空间。
具体来说，DAPO将下裁剪范围εlow​设置为0.2，上裁剪范围εhigh​设置为0.28，从而在保持稳定性的同时提升策略的多样性

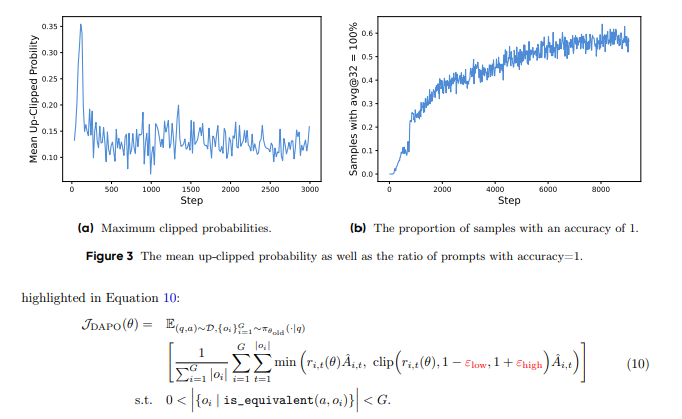
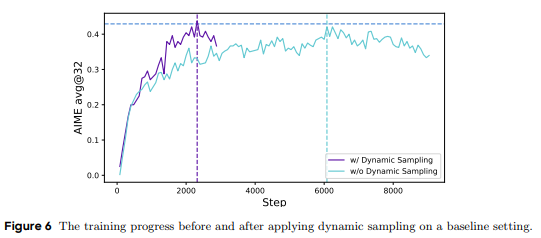
5.3.2 动态采样(The More the Merrier: Dynamic Sampling)

现有的RL算法在面对准确率为1的提示时，往往会出现梯度消失问题。
DAPO通过动态采样策略，过滤掉准确率为1和0的提示，确保每个批次中的提示都具有有效的梯度信号。
实验表明，动态采样不仅提升了训练效率，还加速了模型的收敛。

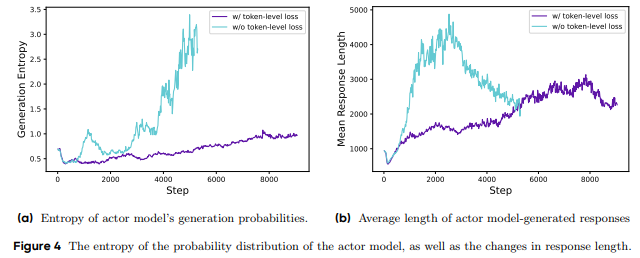
5.3.3 Token-Level策略梯度损失(Rebalancing Act: Token-Level Policy Gradient Loss)

传统的GRPO算法采用样本级损失计算，导致长响应中的token对整体损失的贡献较低。
DAPO引入了Token-Level策略梯度损失，确保长序列中的每个token都能对梯度更新产生同等影响。这一改进不仅提升了训练稳定性，还避免了过长响应中的低质量模式。

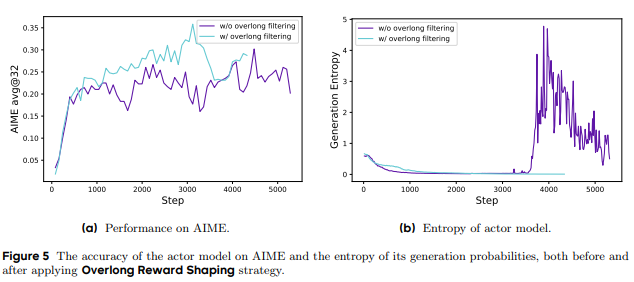
5.3.4 过长奖励整形(Hide and Seek: Overlong Reward Shaping)

在RL训练中，过长的响应通常会被截断，并受到惩罚。然而，这种惩罚可能会引入奖励噪声，干扰训练过程。DAPO提出了软过长惩罚机制，通过长度感知的惩罚区间，逐步增加对过长响应的惩罚，从而减少奖励噪声并稳定训练。

5.3.5 DAPO算法

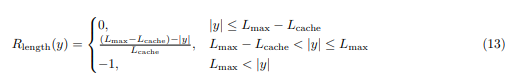
5.4 简单对比GRPO和DAPO

这部分内容是我整理的，对比DeepSeek提出的GRPO（Group Relative Policy Optimization）和DAPO（Decoupled Clip and Dynamic sAmpling Policy Optimization）。

• (1) 策略优化机制
  GRPO：通过群组相对奖励归一化估计优势，消除对价值函数的依赖。其目标函数包含KL散度惩罚项，以限制策略偏离参考模型，但这一设计在长链式推理（CoT）场景中可能限制模型探索空间。
  DAPO：移除了KL散度惩罚，允许模型在长推理任务中自由探索。通过解耦裁剪（Decoupled Clip）调整上下裁剪范围（ low =0.2，high =0.28），提升低概率token的探索能力，有效缓解熵崩溃问题。
• (2) 训练效率优化
  GRPO：在提示样本准确率趋近1时，梯度信号减弱，导致训练效率下降。此外，样本级损失计算可能忽略长序列中关键token的影响。
  DAPO：引入动态采样策略，过滤准确率为0或1的无效样本，确保批次内梯度有效性；采用Token级策略梯度损失，强化长序列中每个token的贡献，避免低质量模式（如重复生成）的干扰。
• (3) 奖励机制设计
  GRPO：依赖传统奖励模型，存在Reward Hacking风险，可能导致模型过度优化局部奖励而非全局推理质量。
  DAPO：采用基于规则的奖励建模，直接以任务最终准确率作为奖励信号（如AIME答案正确性），并结合过长奖励整形（Soft Overlong Punishment），对超长响应施加动态惩罚，减少噪声干扰。

六 Dr. GRPO

论文：Understanding R1-Zero-Like Training: A Critical Perspective，
代码：https://github.com/sail-sg/understand-r1-zero
是oat-zero同一个团队的最新成果。
没错，这虽然是一篇综合分析Base和RL的文章，但我们这里重点关注其中的RL部分，尤其是针对GRPO两个偏差的优化。它的发布时间就在DAPO发布一周后。

6.1 GRPO以及其他方法的问题分析

6.1.1 GRPO两个主要问题

(PPO) 等算法实现:经常包括一个响应长度归一化步骤，这无意中引入了偏向于更长或更短输出的偏差，具体取决于响应的正确性。
(GRPO) 作为一种变体被引入，以在组级别优化策略更新。虽然有效，但 GRPO 因嵌入了影响模型响应长度和质量的微妙优化偏差而受到批评。这些现有技术虽然具有创新性，但显示出局限性，掩盖了 reinforcement learning 的实际收益。

此方法从 GRPO 公式中删除了有问题的长度和奖励归一化项。具体来说，它消除了导致模型更新不平衡的响应长度和标准差缩放因子。修改后的算法可以更公平地计算不同响应和问题类型的梯度。

• 响应级别长度偏差：对积极的advantage，这种偏差导致较短的响应获得更大的梯度更新，从而使策略倾向于在正确答案中优先选择更简洁的表达。相反，对于消极的advantage，由于较长的响应具有更大的 |oi|，因此它们受到的惩罚较小，这导致策略在错误答案中倾向于选择较长的响应。
• 问题难度级别偏差：标准差较低的问题（例如，太简单或太困难的问题，结果奖励几乎全为 1 或 0）在策略更新时会被赋予更高的权重。问题级归一化导致不同问题在目标函数中的权重不同，从而在优化过程中产生了难度偏差。

稍微解释一下第一个，乍一看好像无论短还是长的响应，它们的损失函数在 token 级别上都是均值化的，似乎不会有长度偏差。但其核心问题在于：
由于归一化，导致每个响应（无论长短）的梯度贡献在整体 batch 里是一样的。
但是 advantage计算是基于完整的响应，而不是 token。

• 这就意味着短的响应和长的响应的 advantage 数值大小是一样的，但是短的响应的每个 token 都能获得更强的梯度更新，因为它的 token 数量少，梯度不会被均摊太多。反过来，短的错误答案被惩罚更严重，梯度更新大，模型更快地减少生成这种错误答案的概率；长的错误答案因为梯度更新小，惩罚力度不够，导致模型不太容易抑制长的错误答案。最终导致正确答案更倾向于短的表达，而错误答案更倾向于长的表达。

6.1.2 DAPO也发现了–如何做的

这两个发现和DAPO的其中两个发现不谋而合，非常类似（注意是类似，实际上两者是有明显区别的），前者对应的是Token级别的策略梯度损失，后者对应的是动态采样。

针对响应长度偏差，DAPO将损失计算从样本集改为token级，按token的贡献更新策略。DAPO除以的是所有token数，而Dr .GRPO则除以的是G。
针对问题难度偏差，则通过动态采样，去掉了准确度为1和0的样本，因为一个提示词的一组输出都是1或0时，Advantage直接为0了，没意义。这个和Dr. GRPO其实还是有区别的，后者针对的是几乎为1或0的情况，这种情况下DAPO并不会去掉该提示（样本）。所以，两者其实是可以结合的！

6.1.3 有偏来自预训练的mask？

神奇的是，现有很多框架的PPO（包括GRPO之前的PPO）实现也存在着长度偏差，见下面的代码清单。论文猜测这种偏差可能来源于预训练，因为预训练时token会被填充到固定长度上下文，而按上下文长度归一化损失有助于数值稳定性。但在强化微调阶段，响应长度是不固定的，这在无意中引入了长度偏差。

def masked_mean(tensor, mask, dim):return (tensor * mask).sum(axis=dim) / mask.sum(axis=dim)  # 原始实现（有偏）# 修改后的无偏实现（使用固定常数 MAX_TOKENS）return (tensor * mask).sum(axis=-1) / MAX_TOKENS  ppo_loss = ...  # 计算每个 token 的 PPO 损失
response_mask = ...  # 每个 token 的响应 mask# 方式 1：每个响应长度归一化（如 OpenRLHF）
loss_variant1 = masked_mean(ppo_loss, response_mask, dim=-1).mean()
# 方式 2：整个 batch 归一化（如 trl、verl）
loss_variant2 = masked_mean(ppo_loss, response_mask, dim=None).mean()

6.2 Dr. GRPO

为了解决这两个偏差，Dr. GRPO直接去掉了红色的两项（归一化项）。同时，为了忠实地实现无偏的优化目标，将masked mean 函数中的 mask.sum(axis=dim) 替换为一个常数值（例如生成预算，即最大长度）。

七 CISPO

论文：MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention
代码：https://github.com/MiniMax-AI/MiniMax-M1

7.1 背景：token裁剪的危害

7.1.1 传统PPO算法的局限性

p(x)/q(x)为重要性权重（IW：importance weight）
详见2.2
又可以写成：

是重要性采样权重，用来校正离线策略更新时的分布偏差。

7.1.2 GRPO的改进与不足

GRPO的改进与不足[详见3.2&3.4]
GRPO（Group Relative Policy Optimization）在PPO基础上做了简化，去掉了价值模型，将优势函数定义为相对于组内其他回答的奖励：

7.1.3 发现的核心问题：token裁剪的危害

研究团队在实验中发现了一个严重问题：传统的裁剪操作严重影响了长链思维推理的训练效果。

问题的具体表现
关键token被误伤：那些表示反思行为的token（比如"However"、“Recheck”、“Wait”、“Aha"等）在基础模型中概率很低
推理路径中断：这些token往往是推理路径的"分叉点”，但在策略更新时会产生很高的rit值(重要性采用权重-ppo)
梯度贡献丢失：经过第一次策略更新后，这些token就被裁剪掉了，无法在后续的离线策略梯度更新中发挥作用
这个问题在混合架构模型中尤其严重，进一步阻碍了强化学习的可扩展性。虽然DAPO试图通过提高裁剪上界来缓解这个问题，但在16轮离线策略更新的设置下效果并不理想。

7.2 CISPO思路

核心思想
CISPO（Clipped Importance Sampling Policy Optimization）的核心理念是：不再裁剪token更新，而是裁剪重要性采样权重。

算法推导
首先回顾标准的REINFORCE目标函数：其中 sg（） 表示停止梯度操作。

7.2.1 关键创新：裁剪重要性采样权重

算法优势

• 保留所有token的梯度贡献：特别是在长回答中，每个token都能参与梯度更新
• 减少方差：通过权重裁剪而非token裁剪来稳定训练
• 无需KL惩罚项：类似其他最新工作的简化设计

7.2.2 统一框架

在CISPO目标中引入标记级掩码，允许通过超参数调整来控制是否以及在什么条件下丢弃特定标记的梯度：

掩码的规则：
如果优势>0且重要性权重>1+ε_high，则M=0（不更新）
如果优势<0且重要性权重<1-ε_low，则M=0（不更新）
其他情况M=1（正常更新）
这个统一框架可以灵活表示不同的裁剪策略。

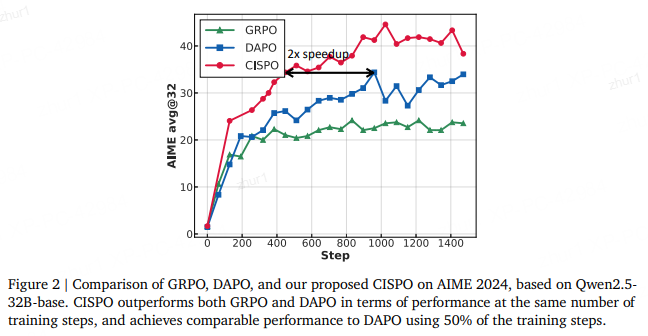
7.3 实验效果

性能优势明显：在相同训练步数下，CISPO显著优于DAPO和GRPO
训练效率大幅提升：CISPO只用50%的训练步数就能达到DAPO的性能水平
稳定性更好：避免了token裁剪带来的不稳定因素

八 GSPO 组序列策略优化

Group Sequence Policy Optimization

8.1 GRPO的问题

然而，作者们敏锐地指出了当前技术路径上的一个核心矛盾：要想通过投入更多计算资源来持续提升模型能力，一个稳定且鲁棒的训练动态是绝对前提。但以GRPO（Group Relative Policy Optimization）为代表的现有先进算法，在训练巨型模型时却暴露出了严重的稳定性问题。论文引用了Qwen和MiniMax在2025年的观测，指出模型崩溃是一种灾难性且不可逆的现象，极大地阻碍了研究者们通过持续的RL训练来探索模型能力的极限。

精准地“诊断”了GRPO算法不稳定的病根。作者们断言，问题出在重要性采样（importance sampling）权重在其算法设计中的根本性误用。GRPO在“词元（token）”级别上进行修正，这种做法引入了高方差的训练噪声。这种噪声会随着生成回复的长度增加而不断累积，并通过裁剪机制被进一步放大，最终导致了灾难性的模型崩溃。

1.2 GSPO

GSPO的“创新之钥”在于其回归了重要性采样的基本原则，将重要性比例的定义从“词元级别”提升到了“序列级别”，即基于整个回复序列的似然度进行计算。此外，GSPO还将奖励归一化为对同一问题的多个回复之间的“优势（advantage）”，确保了序列级别的奖励机制与优化目标保持一致。

实证评估雄辩地证明了GSPO在训练稳定性、效率和最终性能上均显著优于GRPO。尤为关键的是，GSPO内在地解决了大型混合专家（MoE）模型在RL训练中的稳定性挑战，不再需要复杂的稳定化策略（如后文会提到的Routing Replay）。这些卓越的特性，最终转化为Qwen3模型性能的巨大飞跃。作者们展望，GSPO将成为一个强大且可扩展的算法基石，为未来更大规模的RL训练和人工智能发展铺平道路。

1.2.1 核心动机 (Motivation)

作者指出，随着模型尺寸、稀疏性（尤其是在MoE模型中）和生成长度的增加，为了硬件效率最大化，RL训练必须采用大的批次（batch size）。而为了样本效率，通常会将一个大批次数据拆分成多个小批次（mini-batches）进行梯度更新。这个过程天然地引入了“离策略（off-policy）”学习的场景，即用于计算梯度的样本来自于旧策略，而非正在被优化的当前策略。PPO和GRPO中的裁剪机制，正是为了应对这种离策略带来的偏差。

然而，GRPO的问题比单纯的离策略偏差更为根本。作者一针见血地指出，GRPO的目标函数是构建失当的，这个缺陷在训练大型模型处理长回复任务时，会急剧恶化，并最终导致模型崩溃。

问题的根源在于对重要性采样原则的误用。
重要性采样的核心原理（如论文公式(4)所示）是，通过对从行为分布（π_beh）中采出的多个样本（N >> 1）进行加权平均，来估计目标分布（π_tar）下的期望值。
这个权重 π_tar(z) / π_beh(z) 能够有效地修正分布不匹配的问题，但其有效性的前提是基于群体（多个样本）的平均。

反观GRPO，它在每个词元位置 t 上都应用了一个重要性权重 w_i,t(θ)。这个权重是基于单个样本 y_i,t 计算得出的，它完全不具备修正分布失配的能力。

作者犀利地指出，这非但不能实现预期的分布校正，反而向训练梯度中注入了高方差的噪声。这种噪声会随着序列的增长而不断累积，而裁剪机制在试图限制离策略样本影响的同时，也无意中放大了这种噪声的破坏力，最终导致模型训练的“脱轨”和崩溃。一旦崩溃发生，即便是回退到早期的检查点（checkpoint）并细致地调整超参数，也往往无力回天。

这个观察揭示了一个核心原则：优化的基本单元，应该与奖励的基本单元相匹配。既然奖励是给予整个序列的，那么在词元级别进行离策略校正就显得不合时宜且问题重重。这启发作者们必须放弃词元级别的目标，转而在序列的宏观层面直接进行重要性加权和优化。

1.2.3 GSPO

使用序列级别的重要性权重si()
这个权重有着清晰的理论含义：它衡量了由旧策略采样的整个回复序列 y_i，在多大程度上偏离了当前策略，这与授予整个序列的奖励天然对齐。
基于此，GSPO的优化目标被定义为

• 组优势估计Â_i：与GRPO类似，采用公式(7)计算，基于组内相对奖励，无需价值模型。
• 序列级别重要性比例s_i(θ)：这是GSPO的灵魂，如公式(8)定义。它计算的是整个序列的似然度之比。值得注意的是，作者在定义s_i(θ)时引入了长度归一化（即取对数后除以序列长度|y_i|再取指数）。这一精巧的设计旨在降低方差，并使得不同长度回复的s_i(θ)值能被控制在一个统一的数值范围内，避免了短序列的几个词元概率剧变就导致整个s_i(θ)失控，也使得裁剪范围的设定更为简单和通用。

因此，GSPO的裁剪机制也是在整个回复层面生效的，而非针对单个词元。这种设计完美匹配了序列级别的奖励和优化逻辑。

1.2.4 梯度分析

GSPO的梯度（省略裁剪后，如公式(11)所示）：
最终的梯度是序列优势Â_i乘以整个序列的对数似然梯度∇_θ log π_θ(y_i|x)。
这意味着，在一个给定的优秀回复中（Â_i > 0），所有词元都受到同等权重的正向激励，共同为提升整个序列的概率做贡献。
它们“同甘共苦”，命运与共。

GRPO的梯度（如公式(13)所示）：
其梯度中，每个词元的对数似然梯度∇_θ log π_θ(y_i,t|x, y_i,<t)被其各自的、不稳定的重要性权重w_i,t(θ)所加权。
这意味着，即使在同一个优秀回复中，每个词元受到的激励强度也可能天差地别，有些甚至可能因为权重过小而几乎没有更新。
这些不均等的权重累积起来，导致了训练过程的不可预测性。

1.2.5 GSPO-token：一个词元级别的目标变体

论文还考虑了一些特殊场景，比如多轮对话的RL，可能需要更细粒度的、在词元级别上调整优势。
为此，作者设计了一个名为GSPO-token的变体（公式(14)）。其巧妙之处在于，它在计算每个词元的权重s_i,t(θ)时（公式(15)），使用了序列级别的重要性比例s_i(θ)的数值（通过sg，即stop_gradient或detach操作，使其不参与梯度计算），再乘上词元级别的似然比

通过梯度推导（公式(18)），作者证明了一个惊人的结论：
当一个序列中所有词元的优势都相同时（即Â_i,t = Â_i），GSPO-token在优化目标、裁剪条件和理论梯度上，与原始的GSPO是数值等价的。这意味着GSPO-token在享受为每个词元定制优势的灵活性的同时，依然保留了GSPO核心的稳定性和优化特性。

1.3 试验结果

1.3.1 GSPO更稳定,训练效率更高

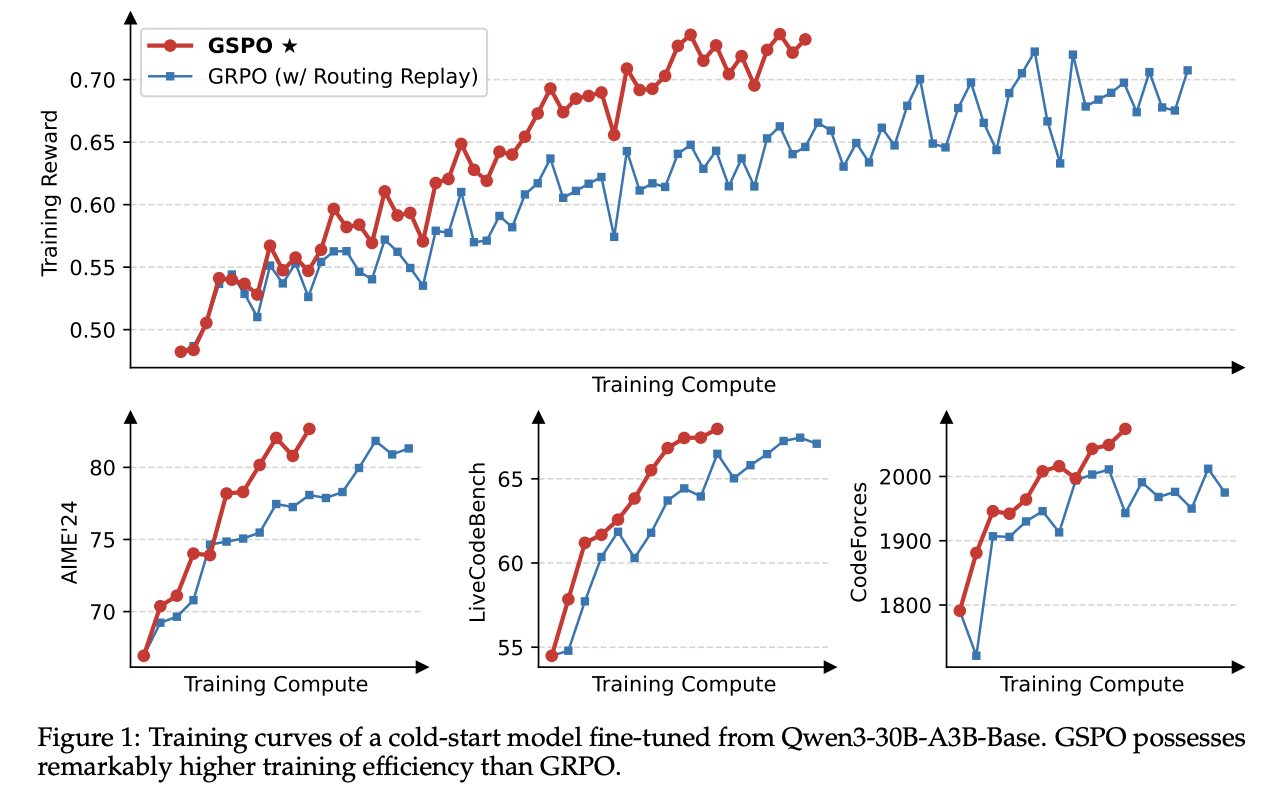
实验在一个从Qwen3-30B-A3B-Base微调的冷启动模型上进行，并在多个高难度基准（AIME’24数学竞赛、LiveCodeBench编程、CodeForces编程Elo评分）上评估模型性能。

图1的训练曲线清晰地显示，GSPO的训练过程全程稳定。随着训练计算量的增加，其性能持续提升。
在同等的训练资源和查询消耗下，GSPO比精心调优的GRPO展现出更高的训练效率，取得了更好的训练奖励和基准测试性能。
最重要的一点是，GRPO在训练MoE模型时，必须依赖一个名为“路由重放（Routing Replay）”的特殊策略才能正常收敛，而GSPO则完全不需要这个额外的复杂机制。

1.3.2 在训练中，GSPO裁剪掉的词元比例更高

下图揭示了一个极为反直觉但极具说服力的现象。在训练中，GSPO裁剪掉的词元比例高达0.15，而GRPO仅为0.0013，两者相差超过两个数量级！

按照传统认知，裁剪掉更多的样本意味着用于训练的有效数据更少，效率应该更低。
但GSPO恰恰相反，它在“抛弃”了远多于GRPO的更新机会后，反而取得了更高的训练效率。
这一发现强有力地佐证了第三部分的核心论断：

• GRPO的词元级别梯度估计是内在充满噪声且低效的。大量的更新其实是在噪声的指导下进行的“无用功”甚至“反向功”。

相比之下，GSPO的序列级别方法虽然看起来“更挑剔”（裁剪比例高），但它提供的学习信号更可靠、更有效。

1.3.3 GSPO对MoE训练的益处

这一节详细解释了为何GSPO是MoE模型RL训练的“特效药”。

• 背景问题：MoE模型在训练时具有稀疏激活的特性。

• 使用GRPO进行RL训练时，会出现一个致命问题——“专家激活不稳定性”。
  具体来说，对于同一个输入，经过一轮梯度更新后，新策略π_θ激活的专家集合，与旧策略π_θ_old激活的专家集合可能有显著不同（论文提到，在48层的Qwen3模型上，差异可达10%）。这导致词元级别的重要性权重w_i,t(θ)剧烈波动，因为计算它的分子和分母可能来自完全不同的子网络，从而破坏了训练的收敛性。

• 过去的解决方案：为了应对这一挑战，团队之前采用了“路由重放（Routing Replay）”策略。
  即在计算w_i,t(θ)时，强制新策略π_θ使用旧策略π_θ_old缓存的专家路由路径。这相当于给模型戴上了“镣铐”，虽然保证了稳定性，但也增加了额外的内存和通信开销，并可能限制了MoE模型的全部潜力。

GSPO的根本性解决：
GSPO的优势在于它只关心整个序列的似然度π_θ(y_i|x)。
由于MoE模型始终保持其作为语言模型的基本能力，整个序列的似然度不会因为专家路由的微小变化而剧烈波动。
因此，GSPO从根本上对专家激活的不稳定性“免疫”，不再需要任何复杂的变通方法。
如图1所示，没有Routing Replay的GSPO依然稳定收敛。这不仅简化和稳定了训练过程，还让MoE模型能够不受束缚地发挥其全部容量。

1.3.4 GSPO对RL基础设施的益处

最后，论文还指出了GSPO带来的一个实际工程上的巨大好处。在实践中，用于训练的引擎（如Megatron-LM）和用于推理采样的引擎（如SGLang, vLLM）在计算精度上存在差异。过去使用GRPO时，为了保证词元级别似然度的精确，通常需要在训练引擎中重新计算一遍由推理引擎采样出的回复的似然度（π_θ_old），这是一个非常耗时的步骤。

而GSPO只依赖于序列级别的似然度，这个宏观指标对微小的精度差异容忍度更高。因此，GSPO使得直接使用推理引擎返回的似然度进行优化成为可能，从而避免了代价高昂的重计算步骤。这在部分 rollout 或多轮 RL 等场景下，以及在训练-推理分离的框架中，能带来显著的效率提升。