【C++算法】77.优先级队列_数据流的中位数

---

题目链接：

295. 数据流的中位数

---

题目描述：

---

解法

解法一：直接sort（会超时）

来一个数就sort一下。通过元素个数找到下标和下标值来求中位数。

解法二：插入排序思想（会超时）

已经有一堆有序的数了，就从后往前扫描，把插入的数插进他合适的位置。

解法三：

大小堆来维护数据流中的中位数。

前面一半数存在大根堆（left堆），后面一半数存在小根堆（right堆）

左边一半元素放到大根堆，堆顶元素就是左边最右侧的元素。

右边一半元素放到小根堆，堆顶元素就是右边最左侧的元素。

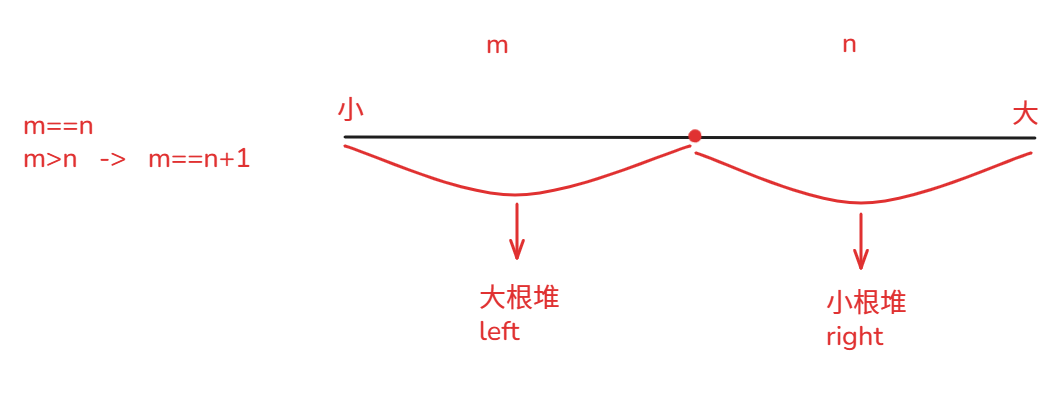
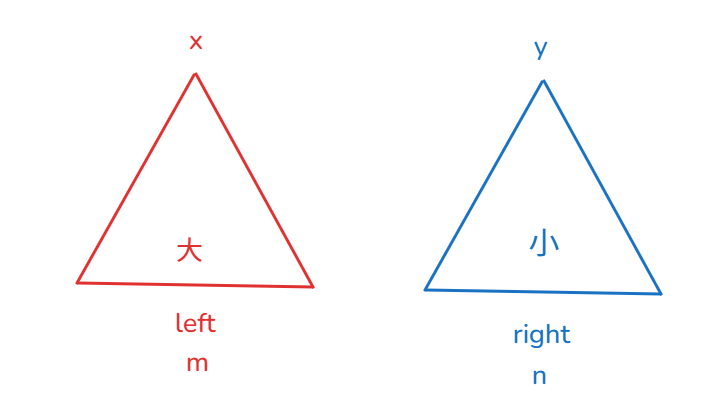
细节问题：add()

需要分类讨论，m== n和m==n+1

1. m== n

   • num<=x或者m==0，num进入left堆
   • num>x，num进入right堆，然后把右边的堆顶元素y进入left堆

2. m==n+1

   • num<=x，num进入left堆，然后把左边的堆顶元素x进入right堆
   • num>x，num进入right堆

---

C++ 算法代码：

class MedianFinder 
{// 维护两个堆：// left 是大根堆，保存较小的一半数据，堆顶是这些数中的最大值priority_queue<int> left;// right 是小根堆，保存较大的一半数据，堆顶是这些数中的最小值// 通过greater<int>比较器实现小根堆priority_queue<int, vector<int>, greater<int>> right;public:// 构造函数MedianFinder() {}// 添加新数字到数据流中void addNum(int num) {// 我们维护的不变量：// 1. left堆中的所有元素 <= right堆中的所有元素// 2. 两个堆的大小差不超过1// 情况1：两堆大小相等时，新元素要么进入left，要么进入right并调整if(left.size() == right.size()){if(left.empty() || num <= left.top()) // 如果新元素应该放入left{left.push(num);}else // 新元素应该放入right，但为了保持平衡，需要将right的最小值转移到left{right.push(num);left.push(right.top());right.pop();}}// 情况2：left比right多一个元素时else{if(num <= left.top()) // 如果新元素应该放入left，需要将left的最大值转移到right以保持平衡{left.push(num);right.push(left.top());left.pop();}else // 新元素大于left.top，直接放入right{right.push(num);}}// 添加结束后，我们始终保持：// 如果总数是偶数，left和right大小相等// 如果总数是奇数，left比right多一个元素}// 获取当前数据流的中位数double findMedian() {// 如果左右堆大小相等（总数为偶数），中位数是两个堆顶的平均值if(left.size() == right.size()) return (left.top() + right.top()) / 2.0;// 如果总数为奇数，中位数就是left堆顶（较小一半的最大值）else return left.top();}
};