当前位置：首页 > backend >正文

【机器学习-2】 | 决策树算法基础/信息熵

backend 2025/7/27 15:43:55

0 序言

本文将系统学习决策树算法，从决策树引入，理解信息熵、ID3与C4.5算法并剖析优缺点。

读完可初步掌握决策树核心原理及经典算法，

下篇再用一个项目实战来加深巩固知识点。

本文就先对此有个概念，理解下大概的原理就可以了，

具体从项目实战来更好去加强巩固。

以下是针对1、2章节补充数据集展示、详细计算及对比分析后的内容，更适合零基础读者理解：

1 决策树引入

1.1 案例背景

为了能更直观理解决策树的应用场景，

这边给出一个案例背景，

通过这个案例背景来更好理解。

我们先给出完整的14天气象数据集，

这里包含4个特征，

分别是outlook、temperature、humidity、windy

和1个标签，Travel决定是否适合旅游。

序号	outlook（天气）	temperature（温度）	humidity（湿度）	windy（风力）	Travel（是否旅游）
1	sunny	hot	high	FALSE	no
2	sunny	hot	high	TRUE	no
3	overcast	hot	high	FALSE	yes
4	rainy	mild	high	FALSE	yes
5	rainy	cool	normal	FALSE	yes
6	rainy	cool	normal	TRUE	no
7	overcast	cool	normal	TRUE	yes
8	sunny	mild	high	FALSE	no
9	sunny	cool	normal	FALSE	yes
10	rainy	mild	normal	FALSE	yes
11	sunny	mild	normal	TRUE	yes
12	overcast	mild	high	TRUE	yes
13	overcast	hot	normal	FALSE	yes
14	rainy	mild	high	TRUE	no

我们的目标是：根据新的气象指标，通过决策树模型预测是否适合出行旅游！！！

1.2 问题本质

决策树的核心实际上就是通过如果……就……的规则拆分数据。

例如，从14天气象数据集中可能提炼出规则：

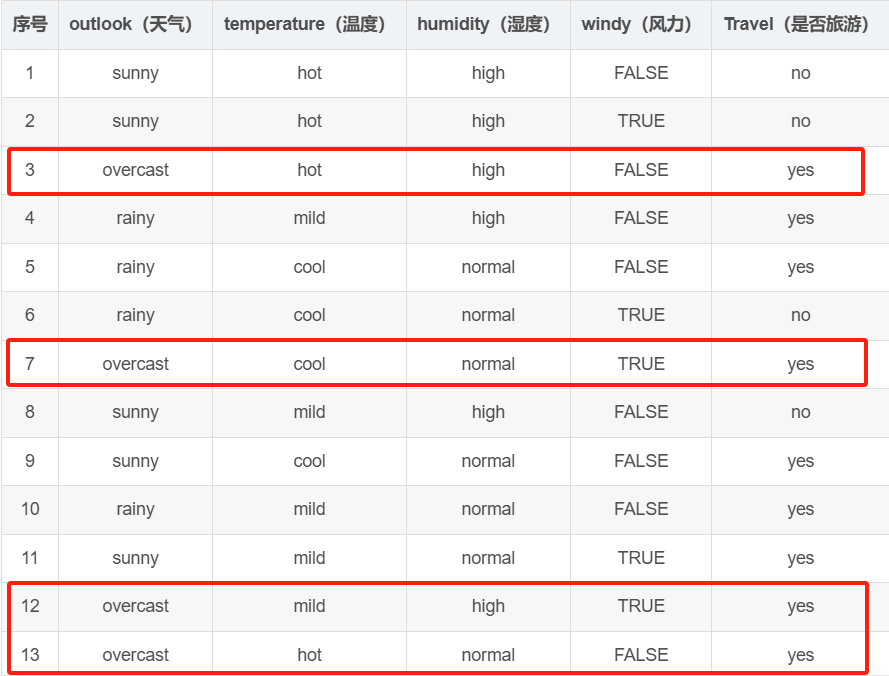
如果outlook=overcast，那么Travel=yes；

如下图红圈圈出来的就是符合要求的。
在这里插入图片描述

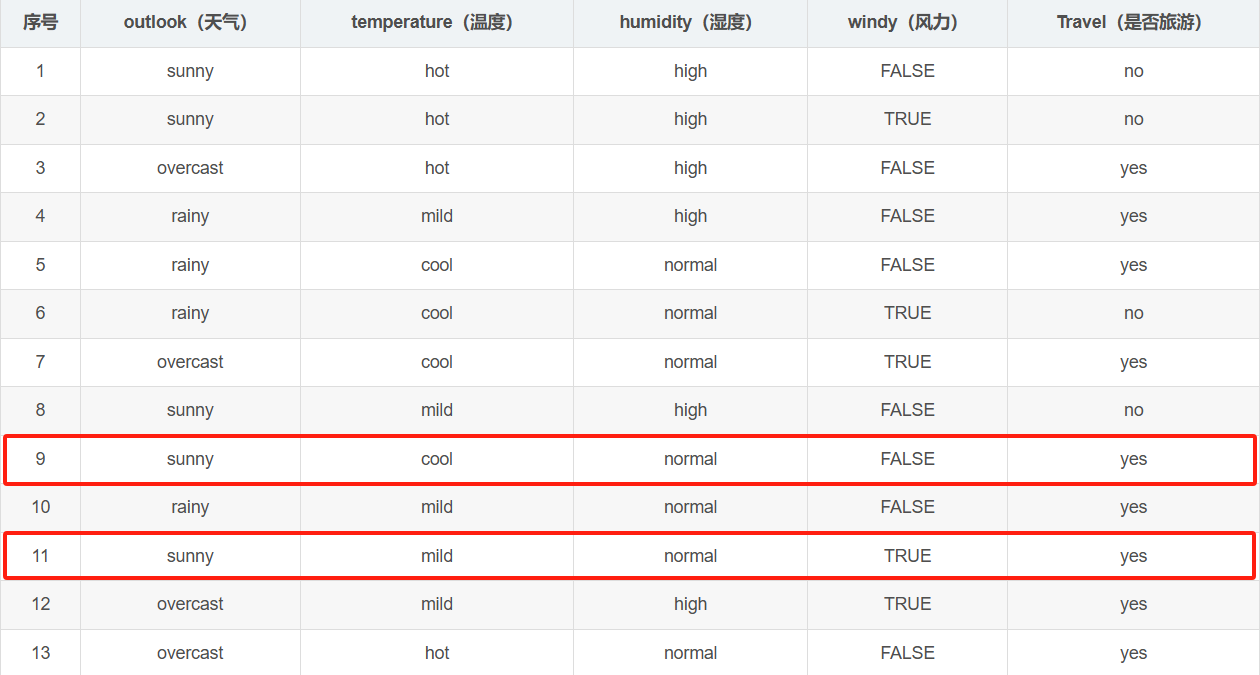
如果outlook=sunny且humidity=normal，那么Travel=yes。

如下图中9、11行均符合要求。

在这里插入图片描述

这些规则的构建依赖于对特征的优先级判断

先按哪个特征拆分数据更能降低分类的不确定性？

这就需要引入信息熵来量化不确定性。

2 信息熵基础

2.1 信息熵定义

熵是无序性（不确定性）的度量指标。

对于一个事件的所有可能结果（如旅游的结果为yes或no），

若各结果的概率为 $p_1, p_2, ..., p_n$ ，

则信息熵公式为：

$,pn)=−p1log⁡2p1−p2log⁡2p2−⋯−pnlog⁡2pnentropy(p_1,p_2,\cdots,p_n) = -p_1\log_2 p_1 - p_2\log_2 p_2 - \cdots - p_n\log_2 p_n$

概率分布越均匀，熵越大（不确定性越高）；
概率分布越集中（某一结果概率接近1），熵越小（不确定性越低）。

2.2 案例计算（基于前面的数据集）

我们以该表1的Travel标签为例，计算初始信息熵，

再对比不同特征分组后的熵，理解熵的变化规律。

步骤1：计算总熵（初始不确定性）

表中共有14条数据，其中：

Travel=yes的样本数：9（序号3、4、5、7、9、10、11、12、13）
Travel=no的样本数：5（序号1、2、6、8、14）

因此，yes的概率 $p_{yes} = 9/14$ ，no的概率 $p_{no} = 5/14$ ，

总熵为：
$entropy_{总} = -\frac{9}{14}\log_2\frac{9}{14} - \frac{5}{14}\log_2\frac{5}{14}$

代入计算:

$log2(9/14)≈−0.609log_2(9/14) \approx -0.609$ ， $log2(5/14)≈−1.485log_2(5/14) \approx -1.485$

因此有，

$entropy_{总} \approx -\frac{9}{14} \times (-0.609) - \frac{5}{14} \times (-1.485) \approx 0.940$

步骤2：按特征分组计算熵（以outlook为例）

outlook有3个取值：sunny、overcast、rainy，

先统计各组中Travel的分布：

sunny（共5条）：

yes=2（序号9、11），no=3（序号1、2、8）→ $p_{yes}=2/5$ ， $p_{no}=3/5$

overcast（共4条）：

yes=4（全为yes）→ $p_{yes}=1$ ， $p_{no}=0$

rainy（共5条）：

yes=3（序号4、5、10），no=2（序号6、14）→ $p_{yes}=3/5$ ， $p_{no}=2/5$

分别计算各组的熵：
$\begin{align*} entropy_{sunny} &= -\frac{2}{5}\log_2\frac{2}{5} - \frac{3}{5}\log_2\frac{3}{5} \approx 0.971 \\ entropy_{overcast} &= -1 \times \log_2 1 - 0 \times \log_2 0 = 0 \quad (\text{因结果确定}) \\ entropy_{rainy} &= -\frac{3}{5}\log_2\frac{3}{5} - \frac{2}{5}\log_2\frac{2}{5} \approx 0.971 \\ \end{align*}$