数据结构——队列

队列

概念与结构

概念：只允许在一端进行插入操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的特性。

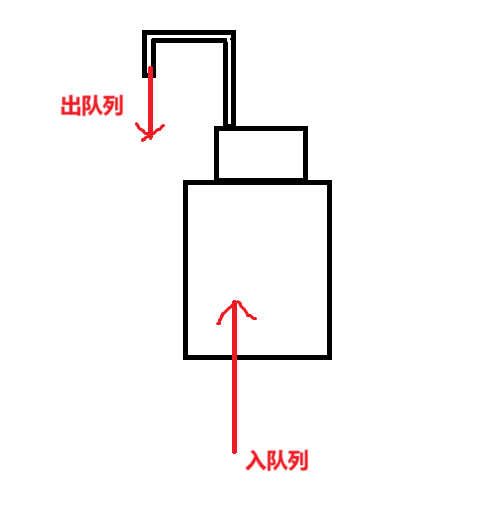
队列：进行插入操作的一端称为队尾。 

出队列：进行删除操作的一端称为队头。

类似一个饮水机：

 

队列底层结构选型

数组

链表

通过上图我们可以看出数组和链表的时间复杂度都差不多，队列可以由数组和链表实现，但是这里我们选择链表，因为如果我们使用数组的结构的话，出数列可以在数组头上出数据，效率会比较低。

队列的实现

我们使用链表，那是否能通过链表把时间复杂度降到O(1)呢？

答案是肯定的。只要我们能把ptail定出来，就可以实现尾插复杂度为O(1)。

队列结点结构

typedef int QDataType;
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;

队列的结构

typedef struct Quene
{struct QueueNode* phead;struct QueueNode* ptail;
}Queue;

初始化队列

void QueueInit(Queue* pq)
{pq->phead = NULL;pq->ptail = NULL;
}

队尾入队列

QNode* BuyQueueNode(QDataType x)
{QNode* cur = (QNode*)malloc(sizeof(QNode));if (cur == NULL){perror("malloc failed!");exit(1);}else{cur->data = x;cur->next = NULL;return cur;}}

void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* cur = BuyQueueNode(x);//如果队列为空if(pq->phead==NULL)pq->phead=pq->ptail = cur;else{pq->ptail->next = cur;pq->ptail = cur;}
}

队头出队列

void QueuePop(Queue* pq)
{assert(pq && pq->phead);if (pq->phead == pq->ptail){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}
}

 获取队列头部元素

QDataType QueueFront(Queue* pq)
{assert(pq && pq->phead);return pq->phead->data;
}

获取队列队尾元素 

QDataType QueueBack(Queue* pq)
{assert(pq && pq->phead);return pq->ptail->data;
}

获取队列中有效元素的个数 

int QueueSize(Queue* pq)
{assert(pq);QNode* pcur = pq->phead;int count = 1;while (pcur->next!=NULL){pcur = pcur->next;count++;}return count;
}

销毁队列 

void QueueDestroy(Queue* pq)
{if (pq->phead == NULL);else{while (pq->phead){QueuePop(pq);}}
}