【文献阅读】Hierarchical Reinforcement Learning: A ComprehensiveSurvey

Acm Computing Surveys (csur)

1区

2021年

分层强化学习：全面综述

分层强化学习（HRL）能够将具有挑战性的长时决策任务自主分解为更简单的子任务。在过去几年里，HRL 研究领域取得了显著发展，产生了大量方法。为了系统地研究 HRL，全面概述这一广阔领域十分必要。

我们对各种 HRL 方法进行综述，涉及学习分层策略、子任务发现、迁移学习以及使用 HRL 的多智能体学习等方面的挑战。本文根据一种新颖的方法分类法进行综述，并基于此提出一系列重要的开放性问题，以推动 HRL 未来的研究。此外，我们在补充材料中概述了一些评估 HRL 方法的合适任务领域，以及 HRL 在实际应用中的有趣示例。

1 引言

人工智能的主要目标之一是开发能够在环境中通过规划最优行动序列来执行各种复杂任务的自主智能体 [80]。强化学习（RL）是一种计算范式，用于学习一种策略，该策略在任务环境的各种状态下采取最优行动，以最大化执行智能体获得的累积奖励 [91]。

为了学习最优策略，智能体通过执行各种状态 - 行动 - 下一个状态的转换序列来探索与任务相关的状态和行动空间。这种序列的平均长度被称为任务时域 1。如果时域较长，且任务涉及较大的状态和行动空间，那么探索空间也会变得很大。

这导致在没有复杂探索技术的情况下，标准 RL 算法 [56, 68, 100] 在这类长时任务上性能较差 [10, 71, 75]。 分层强化学习（HRL）将长时强化学习任务分解为子问题或子任务的层次结构，使得高层策略通过选择最优子任务作为高层行动来学习执行任务。一个子任务本身可能是一个强化学习问题，由低层策略学习解决 [39]。

这种策略层次结构共同决定了智能体的行为。任务分解有效地将原始任务的长时域缩短为子任务序列的较小时域。这是因为每个子任务是一个高层行动，与低层行动相比，它在更长的时间尺度上持续存在，这种属性通常被称为时间抽象 [7, 20, 93]。

时间抽象还可以在更长的时间尺度上实现高效的信用分配 [99]。同时，一个子任务可能本身更容易学习，并且学习到的子任务在 HRL 智能体的训练过程中会导致更结构化的探索 [71]。 这些方面使得 HRL 成为将强化学习扩展到长时任务的有前途的方法 [19, 69, 99]。HRL 算法已被证明在几个长时问题中优于标准 RL，如连续控制 2 [25, 54, 69]、长时游戏 [51, 99]、机器人操作 [28, 33] 等。

不同的实证研究发现，HRL 的性能优势主要归因于使用子任务 / 子目标改进了探索 [43, 71]。 在过去三十年中，HRL 研究取得了显著进展，产生了大量方法来应对各种挑战，如学习层次结构中的策略、子任务的自主发现、迁移学习以及使用 HRL 的多智能体学习。

这给以系统的方式理解该领域的进展带来了很大困难。因此，有必要进行全面的综述，收集和整理重要的 HRL 方法，并为其分类提供通用的分类法。 

本综述与以往的综述有何不同？Barto 等人 [7] 对截至 2003 年的 HRL 进展进行了综述。该综述对经典方法进行了重要概述，主要包括 MAXQ、选项 [93] 和 HAMs [73]。

自该综述发表以来，HRL 领域发生了重大发展，如使用图分析、变分推断、自动编码进行子任务发现，统一 HRL，多智能体 HRL 中的子任务发现，HRL 的迁移学习等。我们的综述与 Barto 等人 [7] 的主要区别在于，除了他们涵盖的经典方法外，我们还回顾了在他们的综述之后出现的新 HRL 方法。

Al - Emran 等人 [21] 从 HRL 实际应用的角度进行了综述。然而，它没有包括一些不适用于所选应用的重要方法，如最近的统一 HRL 技术、HRL 的迁移学习、多智能体 HRL 等。

相比之下，我们对 HRL 方法进行了广泛的综述，并提供了一种与应用无关的通用分类法。 Mendonca 等人 [67] 最近的综述对基于图的子任务发现方法进行了详细回顾。

由于范围有限，他们的综述深入探讨了基于图的子任务发现，但排除了 HRL 研究的其他重要方面，如学习策略层次结构的技术、使用变分推断的子任务发现、统一 HRL、HRL 的迁移学习、多智能体 HRL 等。

然而，我们本着提供 HRL 研究更广阔视角的精神，回顾了所有这些方法以及基于图的子任务发现（第 3.3.1 节）。 本综述的贡献。本综述的目的是全面回顾 HRL 的文献，并概述迄今为止开发的方法。主要贡献如下： 

（1）我们对 HRL 领域迄今为止的工作进行了全面综述。该综述包括学习策略层次结构的方法、独立子任务发现、统一 HRL、HRL 的多任务 / 迁移学习以及多智能体 HRL。 

（2）我们提供了一种新颖的分类法，根据重要的特征维度（如单智能体与多智能体、单任务与多任务、无子任务发现与有子任务发现）来组织 HRL 方法。 

（3）我们确定了一组重要的开放性问题，为 HRL 在可扩展性、效率和理论稳健性方面的未来研究提供方向。 我们致力于使本综述在 HRL 研究的概述和分类方面尽可能全面，而不是对所有现有具体方法进行回顾。HRL 文献过于广泛，无法在有限的篇幅内涵盖。因此，本综述中包含了每个类别的主要代表性方法，而省略了其他类似方法以节省篇幅。 

本文的其余部分组织如下：在第 2 节中，我们回顾强化学习、任务分解和 HRL 的一般概念。第 3 节介绍各种 HRL 方法的分类法和综述，以及它们解决的主要挑战。第 4 节讨论 HRL 未来研究的重要开放性问题。我们在第 5 节中总结本综述。除了本文，我们还提供了一份补充材料文档，其中概述了一些评估和基准测试 HRL 方法的任务领域，并包含了 HRL 在实际问题中实际应用的一些有趣示例。

2 预备知识

2.1 强化学习

RL 指的是学习如何在环境的不同状态下采取行动，以最大化累积未来奖励 [91]，其中奖励是与任务相关的一种反馈形式，是对行动的响应而获得的。目前大多数 RL 研究都建立在马尔可夫决策过程（MDPs）理论基础上 [12]。MDP 是一个使用元组\(<S, A, P, r>\)定义的控制过程。这里，S是环境的状态空间，状态\(s \in S\)表示环境的一种情况。A是智能体可以采取的行动集。\(r: S ×A \to \mathbb{R}\)是作为状态和行动函数获得的数值奖励。行动对未来状态的影响由概率转移函数\(P(s_{t+1} | s_{t}, a_{t}) \to [0,1]\)捕捉，其中\(s_{t+1} \in S\)是在时间t在状态\(s_{t} \in S\)中采取行动\(a_{t} \in A\)后观察到的下一个状态。如果存在一个状态 - 行动对\((s_{t}, a_{t})\)使得\(P(s_{t+1} | s_{t}, a_{t}) ≠1\)，则 MDP 是随机的，因为行动的效果不是确定性的。相反，如果对于每个状态 - 行动对\((s_{t}, a_{t})\)，\(P(s_{t+1} | s_{t}, a_{t})=1\)，则 MDP 是确定性的。智能体根据策略\(\pi: S ×A \to [0,1]\)采取行动。该策略可能是随机的。 智能体与环境的一步交互会产生从当前状态\(s_{t}\)到下一个状态\(s_{t+1}\)的转换，作为经验数据样本\((s_{t}, a_{t}, r_{t}, s_{t+1})\)被观察到。这样的转换序列构成一条轨迹。从任何起始状态和行动对\((s_{t}, a_{t})\)出发的轨迹受策略和状态转换中的随机性影响（根据\(P(s_{t+1} | s_{t}, a_{t})\)）。因此，在状态\(s_{t}\)中采取行动\(a_{t}\)的价值被正式计算为在所有可能轨迹上获得的预期（或平均）累积奖励，如下所示：

这里，\(Q^{\pi}(s_{t}, a_{t})\)是智能体遵循策略\(\pi\)时状态 - 行动对的 Q 值。\(\gamma \in[0,1)\)是折扣因子。\(a ~ \pi(s)\)意味着使用策略\(\pi\)对行动进行采样。RL 的核心目标是学习一个最优策略\(\pi^{*}\)，满足以下条件：

2.2 分层强化学习

从公式 (1) 和 (2) 可以推断，RL 智能体的目标是搜索一种策略，该策略在智能体遵循该策略时，对其可能采取的各种轨迹的累积奖励进行平均最大化。在探索状态和行动空间以学习最优策略时，智能体采取各种轨迹，其预期长度为任务时域（公式 (1) 中时域理论上是无限的，但在实践中可能是有限的）。

如第 1 节所述，当状态和行动空间较大且任务时域较长时，使用标准 RL 方法进行探索变得具有挑战性 [10, 71, 75]。 HRL 提供了一种通过使用通过强化学习学习的策略层次结构将具有挑战性的任务分解为更简单的子任务来执行该任务的机制。

在这样的层次结构中，最高层策略通常选择主要任务的子任务作为其行动 [39]。该策略通过使用在主要任务中获得的奖励，根据其子任务序列进行训练以执行主要任务。在层次结构的较低层，由高层选择的子任务本身是一个强化学习问题。

低层策略使用与其相关的内部奖励（可选地，也可以添加主要任务奖励）学习执行该子任务。最低层策略选择基本行动，此后称为原始行动。 图 1 使用 Russell 等人 [80] 给出的任务分解示例说明了 HRL 的过程。在这个示例中，一个 HRL 智能体分解并执行一个长时任务 “去夏威夷”（GTH）。HRL 智能体由一个策略层次结构组成。任务策略\(\pi_{GTH}\)将原始任务 GTH 分解为一系列最高层子任务 “预订机票”（BT）、“去机场”（GTA）等。任务策略最初选择 BT。

然后，BT 执行多个时间步，直到在时间\(T_{3}\)终止。在此期间，子任务 BT 的策略\(\pi_{BT}\)本身依次选择不同的较短子任务。这些子任务是 “打开预订网站”（OBW）、“输入航班信息”（EFI）等。在\(T_{3}\)BT 终止后，任务策略选择 GTA，GTA 本身选择一个较短的子任务 “去出租车站”（GTS）。

在每个时间步，最低层子任务策略选择一个原始行动a，例如由\(\pi_{OBW}\)、\(\pi_{EFI}\)、\(\pi_{GTS}\)等选择。HRL 智能体对原始行动做出响应，获得任务奖励\(r^{GTH}\)，该奖励在不同时间尺度上累积并给予不同层次。对于低于最高层的策略，任务奖励可能是可选的，这些策略可以使用与子任务相关的奖励进行训练。以这种方式，HRL 过程在时间上持续进行，直到 GTH 完成。

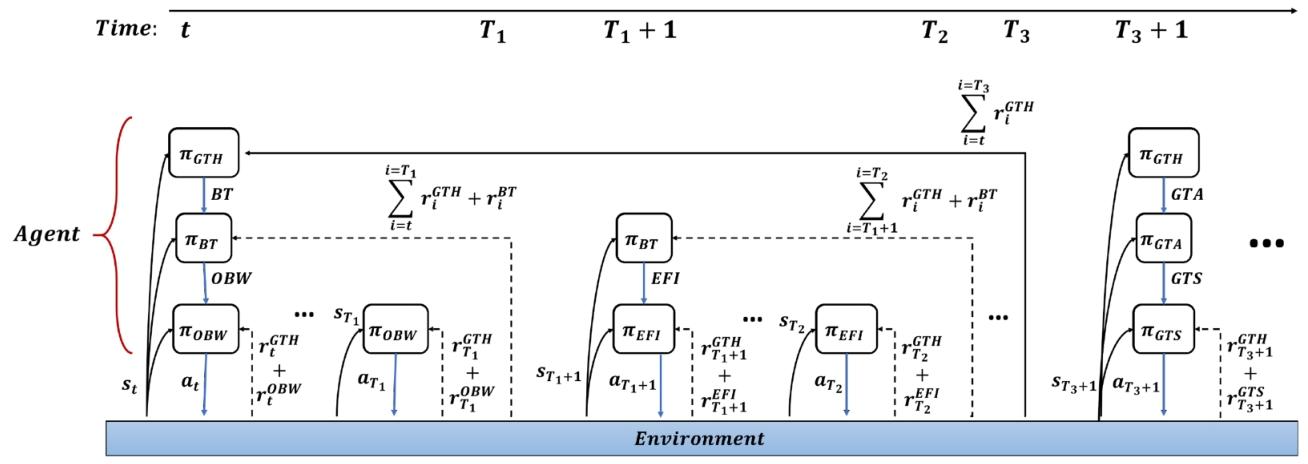
图 1 分层强化学习的时间过程

展示了智能体（Agent）与环境（Environment）在不同时间步交互的分层强化学习过程，以下是详细解释：

整体框架

图中展示了一个智能体在环境中随时间进行决策和行动的过程，时间轴从左到右延伸，标记了不同的时间点t、\(T_1\)、\(T_1 + 1\)、\(T_2\)、\(T_3\)、\(T_3 + 1\) 等。智能体内部包含多个层次的策略，这些策略在不同时间步指导智能体的行动，并从环境中获取奖励。

智能体的策略层次

• 顶层策略\(\pi_{GTH}\) ：是智能体的最高层策略，负责在不同时间点做出高层决策，选择下一层要执行的策略。例如在时间t选择\(\pi_{BT}\)，在时间\(T_3 + 1\)选择\(\pi_{GTA}\) 。
• 中间层策略（以\(\pi_{BT}\)为例） ：由顶层策略\(\pi_{GTH}\)调用，在其执行期间进一步选择更底层的策略。如\(\pi_{BT}\)在时间t到\(T_1\)期间调用\(\pi_{OBW}\)，在时间\(T_1 + 1\)到\(T_2\)期间调用\(\pi_{EFI}\) 。
• 底层策略（以\(\pi_{OBW}\)、\(\pi_{EFI}\)为例） ：根据上层策略的指示，在环境中执行具体行动。如\(\pi_{OBW}\)在状态\(s_t\)执行行动\(a_t\) ，\(\pi_{EFI}\)在状态\(s_{T_1 + 1}\)执行行动\(a_{T_1 + 1}\) 。

行动与状态转移

• 行动选择：在每个时间步，底层策略根据当前状态选择行动。例如在状态\(s_t\)，\(\pi_{OBW}\)选择行动\(a_t\)；在状态\(s_{T_1 + 1}\)，\(\pi_{EFI}\)选择行动\(a_{T_1 + 1}\) 。
• 状态转移：智能体执行行动后，环境状态发生变化。如执行\(a_t\)后，状态从\(s_t\)转移到\(s_{T_1}\)；执行\(a_{T_1 + 1}\)后，状态从\(s_{T_1 + 1}\)转移到\(s_{T_2}\) 。

奖励机制

• 即时奖励：每个底层策略执行行动时会获得即时奖励。如\(\pi_{OBW}\)在时间t获得奖励\(r_t^{GTH}+r_t^{OBW}\) ，在时间\(T_1\)获得奖励\(r_{T_1}^{GTH}+r_{T_1}^{OBW}\) ；\(\pi_{EFI}\)在时间\(T_1 + 1\)获得奖励\(r_{T_1 + 1}^{GTH}+r_{T_1 + 1}^{EFI}\) ，在时间\(T_2\)获得奖励\(r_{T_2}^{GTH}+r_{T_2}^{EFI}\) 。
• 累积奖励：在特定时间段内，中间层策略也会积累奖励。例如在时间t到\(T_1\)，\(\pi_{BT}\)积累奖励\(\sum_{i = t}^{i = T_1}r_i^{GTH}+r_t^{BT}\) ；在时间\(T_1 + 1\)到\(T_2\) ，\(\pi_{BT}\)积累奖励\(\sum_{i = T_1 + 1}^{i = T_2}r_i^{GTH}+r_i^{BT}\) 。

这种分层结构使得智能体可以在不同层次上进行决策，通过各层策略的协同工作，在环境中逐步学习并优化行动，以获取最大的累积奖励。

2.2.1 子任务的形式定义

本子节提供了 HRL 形式背景下子任务的定义。这个定义是不同 HRL 方法定义子任务的不同方式的总结。因此，它应被视为一个通用定义。特定的 HRL 方法可能只使用通用定义的选择性组件。具体细节将在第 3 节中进一步讨论。 

首先，我们将主要的长时任务表示为\(\Gamma\)，任务策略表示为\(\pi_{I}\)。任务策略位于层次结构的顶部，例如图 1 中的\(\pi_{GTH}\)。子任务表示为\(\omega\)。它使用以下组件定义：

• \(\pi_{\omega}\)，即子任务的策略。它将环境状态映射到原始行动或\(\omega\)的子任务 [93]。
• 目标组件：
  • \(r_{\omega}\)，用于训练\(\pi_{\omega}\)的子任务奖励。这通常与主要任务相关的奖励不同 [51, 69, 99]。
  • \(g_{\omega}\)，与\(\omega\)相关的一个子目标或一组子目标。子目标可能是状态\(s \in S\) [64, 84, 87]、状态的抽象形式 [54, 69]、学习到的嵌入 [70, 88, 99] 等。奖励\(r_{\omega}\)可能根据子目标来定义。
• 执行组件：
  • \(I_{\omega}\)，\(\omega\)的启动条件。它可以定义为一组状态，在这些状态中可以选择执行\(\omega\) [93]，也可以定义为一个函数，该函数调制在特定状态下选择\(\omega\)的概率 [45]，还可以定义为一组逻辑条件 [74] 等。
  • \(\beta_{\omega}\)，\(\omega\)的终止条件。它可以定义为一组状态，如果\(\omega\)正在执行，则应在这些状态中终止 [19, 51]，也可以定义为一个函数，该函数调制在特定状态下终止\(\omega\)的概率 [3, 93]，还可以定义为一个固定的时间限制 [54, 69] 等。如果定义了\(g_{\omega}\)，那么子目标状态通常也包含在\(\omega\)必须终止的状态中 [51]。 在本文的其余部分，“子任务” 一词应按照这个形式定义来理解。

2.2.2 基于半马尔可夫决策过程的 HRL 形式化

HRL 基于半马尔可夫决策过程（SMDP）理论进行形式化 [9]。SMDP 是一个随机控制过程，类似于 MDP（第 2.1 节），但与 MDP 不同的是，它还涉及选择行动后执行该行动的时间概念。在 HRL 的背景下，具有时间概念的行动是子任务。从状态\(s_{t} \in S\)开始，假设智能体选择一个子任务\(\omega_{t} \in \Omega\)，其中\(\Omega\)是子任务集（或子任务空间）。那么，SMDP 的转移函数定义为一个联合分布： 

(3)\) 这里，\(c_{\omega_{t}}\)表示从状态\(s_{t}\)开始执行\(\omega_{t}\)的时间步数。\(c_{\omega_{s}}\)实际上由终止条件\(\beta_{\omega_{t}}\)确定，\(\beta_{\omega_{t}}\)是在第 2.2.1 节中定义的执行组件之一。 从状态\(s_{t}\)开始执行子任务\(\omega_{t}\)获得的奖励表示为\(R(s_{t}, \omega_{t})\)，计算如下： 

公式 (4) 表明，奖励\(R(s_{t}, \omega_{t})\)等于在从时间t开始遵循子任务策略\(\pi_{\omega_{t}}\)直到\(\omega_{t}\)在 (c_{\omega_{t个时间步后终止期间获得的预期累积奖励。现在，一个最优任务策略将是导致以下期望的最大 Q 值的策略：

对于所有\(s \in S\)和所有\(\omega \in \Omega\)。
应该注意的是，公式 (5) 中的 Q 值还取决于\(R(s_{t}, \omega_{t})\)和\(P(s_{t+c_{\omega_{t}}}, c_{\omega_{t}} | s_{t}, \omega_{t})\) 。这两个量由使用其策略\(\pi_{\omega_{t}}\)执行\(\omega_{t}\)来确定。因此，智能体实际上需要在任务分解层次结构的不同级别学习多个策略，包括\(\pi_{\Gamma}\)和所有子任务的策略（例如，图 1）。我们扩展了用于多级层次结构的子任务和策略的符号，如下所定义。请参考图 2，了解这些符号在具有三级层次结构的 HRL 智能体上下文中的示例。

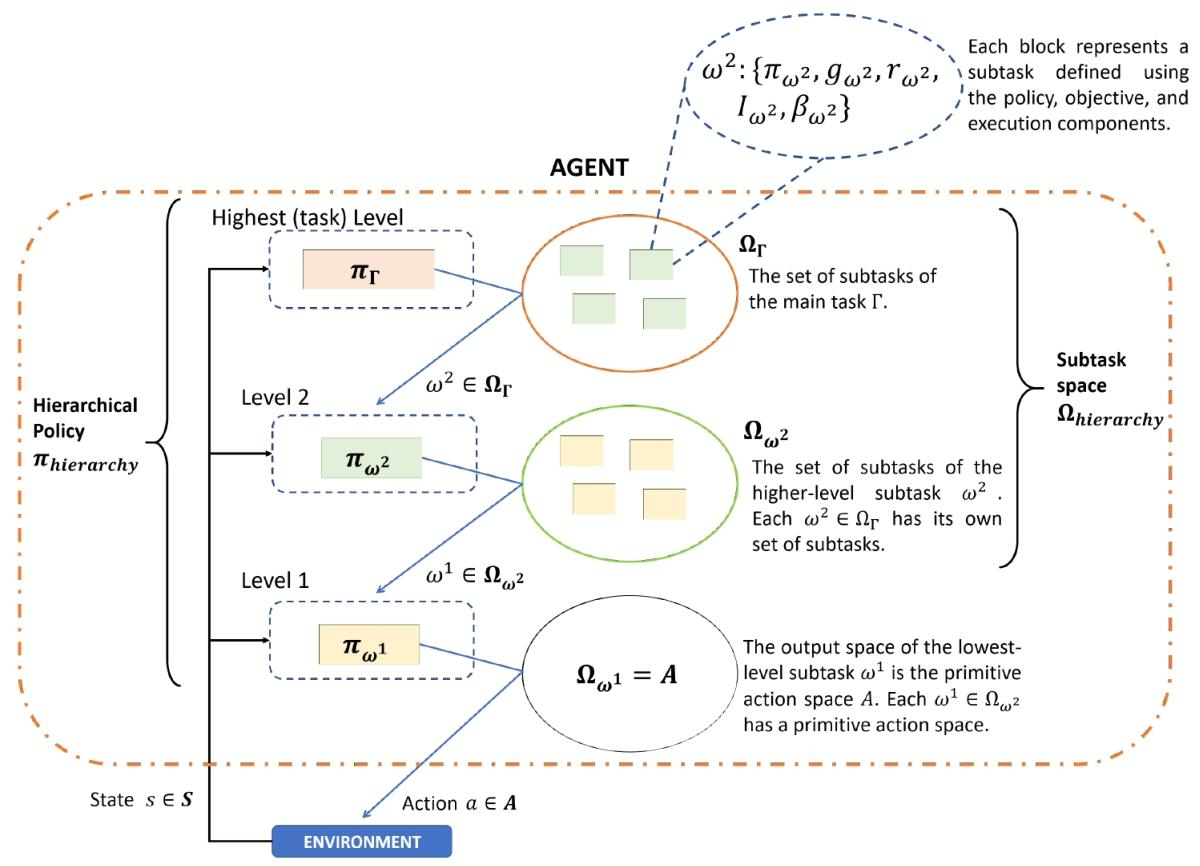
图 2 分层强化学习智能体的概念。此图展示的是一个三级层次结构，但该概念可以扩展到超过三级。

• \(\omega^{l}\)：层次结构第l级的子任务。
• \(\Omega_{\omega^{l}}\)：子任务\(\omega^{l}\)下的子任务集，使得\(\omega^{l - 1} \in \Omega_{\omega^{l}}\)。
• \(\pi_{\omega^{l}}: S ×\Omega_{\omega^{l}} \to [0,1]\)：子任务\(\omega^{l}\)的策略。换句话说，\(\omega^{l - 1}\)由\(\pi_{\omega^{l}}\)选择。
• \(\Omega_{\omega^{1}} = A\)，即最低级别（\(l = 1\)）子任务的输出空间是原始行动空间A。 \(\pi_{\Gamma}\)和\(\Omega_{\Gamma}\)分别表示主要任务策略和最高级别的子任务集。 综合以上所有定义，HRL 智能体有两个主要部分：
• 子任务空间\((\Omega_{hierarchy})\)。这是层次结构中使用的所有子任务的超集，即\(\Omega_{hierarchy} = {\Omega_{\omega^{2}}, \Omega_{\omega^{3}}, \Omega_{\omega^{4}}, \cdots, \Omega_{\Gamma}}\)。
• 分层策略\((\pi_{hierarchy})\)。HRL 智能体采取的原始行动是子任务递归选择的结果。考虑图 2 中描绘的三级层次结构。在这个层次结构中，主要策略\(\pi_{\Gamma}\)选择一个 2 级子任务，即\(\omega^{2} = \pi_{\Gamma}(s)\)，其中\(\omega^{2} \in \Omega_{\Gamma}\)。\(\omega^{2}\)的策略根据\(\beta_{\omega^{2}}\)执行，直到其终止。它选择最低级别的子任务\(\omega^{1} = \pi_{\omega^{2}}(s)\)，其中\(\omega^{1} \in \Omega_{\omega^{2}}\)。\(\omega^{1}\)的策略根据\(\beta_{\omega^{1}}\)执行，直到其终止。这个最低级别的策略选择一个原始行动，即\(a = \pi_{\omega^{1}}(s)\)。从\(\pi_{\omega^{1}}\)的这个完整的状态到子任务再到行动的映射称为分层策略，表示为\(\pi_{hierarchy}\)。现在，HRL 智能体整体采取的原始行动可以等效地表示为\(a = \pi_{hierarchy}(s)\)。这个描述可以扩展到超过三级的层次结构。 基于上述定义，HRL 智能体获得的预期折扣累积奖励可以写成：
• 其中\(a \sim \pi_{hierarchy } | \Omega_{hierarchy }\)表示根据可用的子任务空间\(\Omega_{hierarchy}\)使用分层策略\(\pi_{hierarchy}\)对原始行动a进行采样。

展示了分层强化学习（HRL）智能体的结构，描述了智能体如何通过分层策略在环境中执行任务

整体框架：图中主要分为智能体（AGENT）和环境（ENVIRONMENT）两大部分。智能体内部采用分层策略（Hierarchical Policy \(\pi_{hierarchy}\)），由不同层次的子任务和对应的策略组成，通过与环境交互来执行任务。

智能体的分层结构

• 最高（任务）层（Highest (task) Level）
  • 策略\(\pi_{\Gamma}\) ：位于最高层，负责从主任务\(\Gamma\)的子任务集\(\Omega_{\Gamma}\)中选择子任务\(\omega^{2}\) 。
  • 子任务集\(\Omega_{\Gamma}\) ：主任务\(\Gamma\)的子任务集合，每个子任务\(\omega^{2}\)由策略\(\pi_{\omega^{2}}\)、目标\(g_{\omega^{2}}\) 、奖励\(r_{\omega^{2}}\) 、启动条件\(I_{\omega^{2}}\)和终止条件\(\beta_{\omega^{2}}\) 定义 。
• 第二层（Level 2）
  • 策略\(\pi_{\omega^{2}}\) ：根据上层策略\(\pi_{\Gamma}\)选择的子任务\(\omega^{2}\) ，从\(\omega^{2}\)对应的子任务集\(\Omega_{\omega^{2}}\)中进一步选择子任务\(\omega^{1}\) 。
  • 子任务集\(\Omega_{\omega^{2}}\) ：每个\(\omega^{2} \in \Omega_{\Gamma}\)都有自己的子任务集，包含多个子任务 。
• 第一层（Level 1）
  • 策略\(\pi_{\omega^{1}}\) ：根据上层策略\(\pi_{\omega^{2}}\)选择的子任务\(\omega^{1}\) ，在原始行动空间A中选择具体行动a 。
  • 子任务集\(\Omega_{\omega^{1}}\) ：最低层子任务\(\omega^{1}\)的输出空间就是原始行动空间A ，即每个\(\omega^{1} \in \Omega_{\omega^{2}}\)都对应一个原始行动空间 。

子任务空间（Subtask space \(\Omega_{hierarchy}\)）：包含了智能体层次结构中使用的所有子任务，是一个超集，涵盖了\(\Omega_{\omega^{2}}\) 、\(\Omega_{\omega^{1}}\)等不同层次的子任务集合。每个子任务块都用策略、目标和执行组件来定义，体现了子任务的具体属性和执行方式。

智能体与环境的交互：智能体接收来自环境的状态\(s \in S\) ，通过分层策略\(\pi_{hierarchy}\)从高层到低层逐步选择子任务和行动，最终在环境中执行行动\(a \in A\) ，并根据环境反馈的奖励等信息进行学习和优化策略。

2.2.3 HRL 的问题定义

HRL 的一般问题定义是找到最优分层策略\(\pi_{hierarchy}^{*}\)和最优子任务空间\(\Omega_{hierarchy}^{*}\)，作为以下问题的解决方案：

公式 (7) 中表达的 HRL 问题可以分为两部分。第一部分是学习分层策略，指的是在可用子任务空间的条件下找到最优分层策略（即\(\underset{\pi_{hierarchy } | \Omega_{hierarchy }}{\arg\max}\)）。

这是至关重要的，因为分层策略决定了 HRL 智能体在任何给定任务上的行为。\(\pi_{hierarchy}\)各级的策略可以以端到端的方式同时学习 [3, 21, 52, 54, 69]，也可以以自底向上的方式一次学习一级 [25, 28, 60]。第二部分是子任务发现，指的是使用 HRL 智能体的经验数据自动找到最优子任务空间（即\(\underset{\Omega_{hierarchy }}{\arg\max}\) ）。

子任务发现不是必需的，因为子任务空间可以使用精确的领域知识手工制作。然而，对于不依赖于手动制作的通用 HRL 来说，它是必要的。

2.3 常用术语和概念的定义

这里定义了本文其余部分中常见的一些重要术语和概念。

• 技能：“技能” 是一个语义术语，用于指代学习来执行子任务的原始行动策略，从这个意义上说，这样的策略代表了智能体做好某件事情的能力。
• 通用策略：在本文中，“通用策略” 是指一种策略，它可以通过将相应的子目标 [19, 54, 99] 或指令 [41] 作为输入来学习所有可能的子任务，即\(\pi_{\omega}(s)=\pi(s, g_{\omega})\)，其中\(\pi(s, g_{\omega})\)是通用策略。
• 状态抽象：状态抽象是一种映射，例如\(\phi\)，它将原始状态空间S映射到某个有限的低维抽象空间。如果对于一对\(s, s' \in S\)，\(\phi(s)=\phi(s')\)，那么原始状态空间中的这两个状态在抽象空间中由同一个状态表示。
• 奖励抽象：奖励抽象意味着作为主要任务一部分给出的奖励对子任务策略隐藏，仅由最高层策略接收。
• “全局” 启动条件：在第 3 节提供的表格中对子任务的定义中，无论何时在启动条件\(I_{\omega}\)的引用中使用 “全局” 一词，都意味着子任务可以在全局状态空间的任何状态下被选择执行。

3 分层强化学习方法

本节对为分层强化学习开发的广泛方法进行回顾和分类。回顾是根据图 3 中描绘的一种新颖的分类法进行组织的。为了设计这种分类法，所调查的 HRL 方法沿着三个独立的维度进行排列，如下所示：

（1）有子任务发现或没有子任务发现的方法。

（2）训练单个智能体或多个智能体的方法。

（3）在单个任务或多个任务上学习的方法。这个三维空间可以有八种可能的划分（八分圆）。我们发现大多数 HRL 方法位于其中六个划分中。这些方法进一步根据它们解决的主要挑战分为五个主要类别 ——LHP、UNI、ISD、MAHRL 和 TransferHRL。划分和类别如下： 

（1）单智能体、单任务、无子任务发现：这个划分中的方法被归类为一个主要类别，称为学习分层策略（LHP）。LHP 方法解决了在不涉及子任务发现的情况下学习 HRL 智能体分层策略\(\pi_{hierarchy}\)的挑战。它们使用手工制作的子任务。 

（2）单智能体、单任务、有子任务发现：这个划分中的方法被分为两个主要类别。第一个类别称为与子任务发现统一的学习分层策略（UNI）。UNI 方法解决了以统一或端到端的方式学习子任务空间\(\Omega_{hierarchy}\)和分层策略\(\pi_{hierarchy}\)的挑战。第二个类别称为独立子任务发现（ISD）。

这个类别的方法解决了独立于任何特定任务发现与任务无关的子任务的挑战。子任务发现通常在预训练阶段进行，然后使用这些子任务在下游任务上学习 HRL 智能体。 

（3）多智能体、单任务、无子任务发现。 

（4）多智能体、单任务、有子任务发现。划分 3 和 4 中的方法被归类为一个类别，称为多智能体 HRL（MAHRL）。MAHRL 方法广泛解决了在单个联合任务上学习协调多个 HRL 智能体的挑战。 

（5）单智能体、多任务、无子任务发现。 

（6）单智能体、多任务、有子任务发现。划分 5 和 6 中的方法被归类为一个类别，称为使用 HRL 的迁移学习（TransferHRL）。TransferHRL 方法广泛解决了学习在多个任务之间转移 HRL 智能体的分层策略、子任务或其他知识的挑战，其中子任务可以是手工制作的，也可以是在多个任务上从头开始发现的。 

我们在其余两个划分中没有找到大量的工作，这两个划分代表了多智能体、多任务、有 / 无子任务发现的方法。以下小节将详细讨论上述主要类别、它们相关的挑战以及解决这些挑战的方法。在继续之前，我们鼓励读者回顾第 2.3 节中提供的常用术语的重要定义。

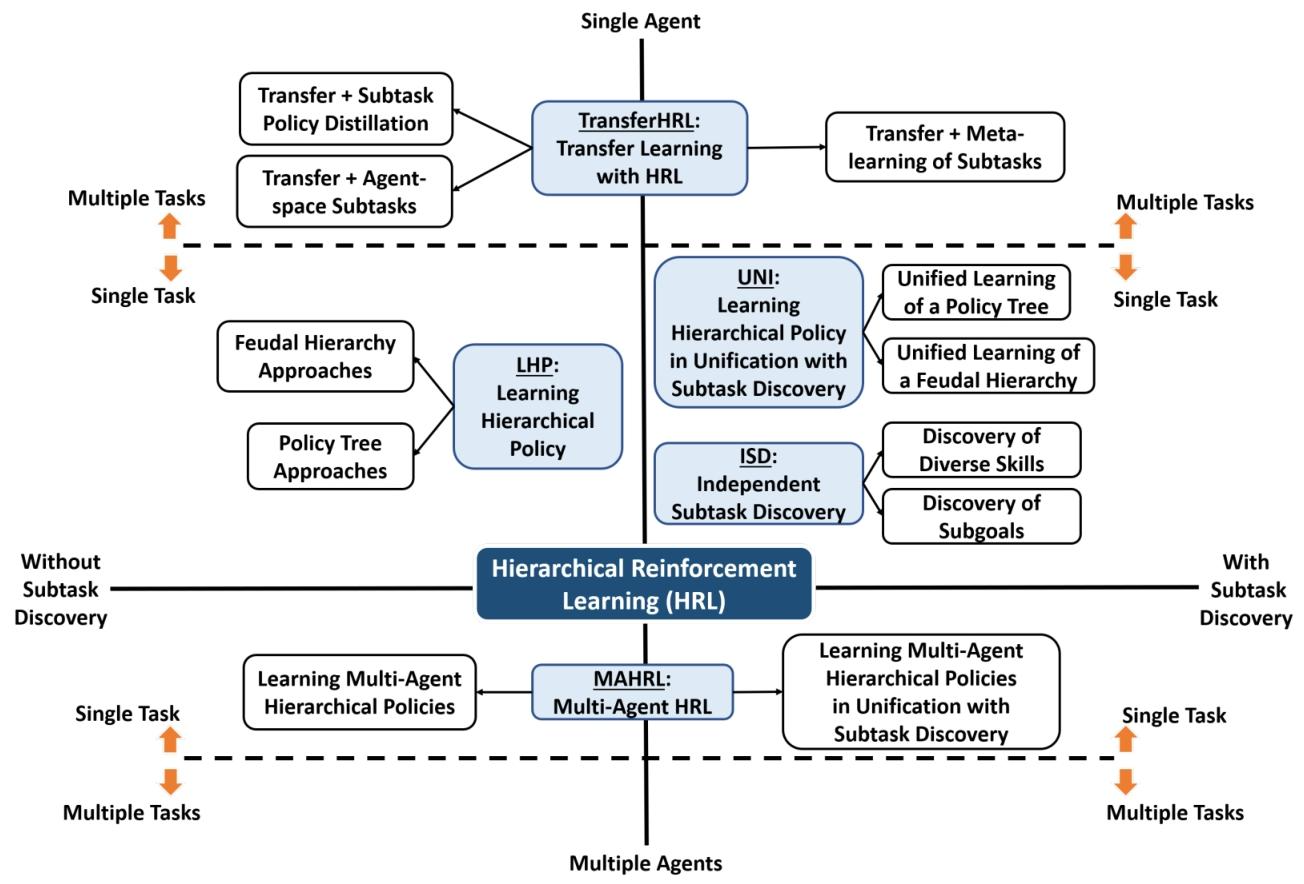
图 3 HRL 方法的分类。这些方法沿着以下三个维度排列：有无子任务发现、单智能体或多智能体、单任务或多任务。

3.1 学习分层策略（LHP）

本小节回顾在单智能体和单任务设置下，解决学习分层策略\(\pi_{hierarchy}\)而无子任务发现挑战的方法。即使子任务是手工制作的，学习分层策略也是一个具有挑战性的问题。这是因为任何学习分层策略的方法都必须解决以下关键问题：仔细设计算法来学习层次结构各级的策略（包括奖励传播、价值函数分解、状态 / 行动空间设计等），处理由于策略同时变化而导致的非平稳性，确保分层策略整体的最优性，分层策略的可解释性等其他问题。

请参考表 1 对 LHP 方法的总结。 LHP 方法大致可以分为两个子类。第一个子类称为封建等级结构，其中高层策略的行动空间由对应于各种子任务的子目标组成。高层策略选择的子目标作为低层通用策略 3 的输入。这个低层通用策略的目标是实现输入的子目标。

每个级别的通用策略可以被视为一个子智能体（作为 HRL 智能体的一部分），它可以执行该级别所有可能的子任务。这导致了 “管理者” 子智能体（高层策略）指导 “工作者” 子智能体（低层策略）的封建概念 [19, 51, 69]。相应的方法将在第 3.1.1 节中讨论。 第二个子类称为策略树。这个名称是为了本综述中的分类目的而引入的，在 HRL 文献中可能找不到。

在策略树中，高层策略的行动空间由子任务的不同低层策略组成。子任务不是由单个通用低层策略表示；相反，每个子任务都有一个单独的策略。高层策略和各种低层策略形成一个 “树”。高层策略直接选择一个低层策略进行执行，而无需中间子目标 [73, 93]。相应的方法将在第 3.1.2 节中讨论。 表 1 学习分层策略（LHP）的方法

3.1.1 封建等级结构方法

Dayan 和 Hinton [19] 引入了基础的封建等级结构，称为封建强化学习（封建 RL）。封建 RL 简要描述如下：一个高层管理者设置一个子任务，由低层工作者执行。这是一种成对关系，使得如果等级结构有超过两个级别，工作者就成为其下一级的管理者。管理者通过子目标将子任务传达给工作者，其中子目标只是原始或抽象状态空间中的一个状态。

工作者的目标是到达给定的子目标。每个级别的工作者都是一个通用策略。任务奖励可能仅由最高层的管理者观察到，而其他级别的工作者使用到达子目标的奖励进行学习。作者在网格世界环境中的迷宫导航任务上评估封建 RL，使用在不同空间距离的预定义状态作为子目标。封建 RL 比标准 Q 学习更快地收敛到迷宫中到达主要目标状态的更短路径。

本文中讨论的其余封建等级结构方法都基于上述封建 RL 的概念。 Kulkarni 等人 [51] 提出了一种深度 HRL 方法，由表示管理者和工作者的两级深度 Q 网络（DQNs）[68] 组成。管理者网络从一组预定义的子目标中选择一个子目标。它使用任务奖励进行学习。工作者网络将子目标作为输入，并选择原始行动来实现子目标。它使用到达子目标的奖励进行学习。

子目标可以是原始状态或状态的抽象表示，例如从代表原始状态的图像中提取的对象。用于评估的任务之一是 Atari 蒙特祖玛的复仇，在这个任务中，标准 DQN 在 200 万个时间步内几乎没有获得任何奖励。然而，具有预定义子目标的深度 HRL 随着训练的进行逐渐获得更高的奖励。 同时学习多层策略会导致非平稳性问题 [54, 69]。

这意味着由执行低层策略生成并由高层策略观察到的状态 - 行动 - 下一个状态转换数据，即使在环境的相同状态下选择相同的子目标，在不同的时间实例中也会有所不同。这是因为低层策略不是平稳的，并且它对（状态，子目标）对的响应在学习过程中会发生变化。非平稳性可能会导致许多无用的数据样本，为了高效学习，需要解决这个问题。

为了解决非平稳性问题，Nachum 等人 [69] 提出了一种带有子目标重新标记机制的两级封建等级结构。这种方法称为带有离策略校正的分层强化学习（HIRO）。HIRO 中的子目标重新标记可以描述如下：

一个两级 HRL 智能体与环境交互并收集经验数据。这些数据由高层策略的转换元组\((s_{t}, g_{t}, \sum r_{t: t + c}, s_{t + c})\)组成，其中r是任务奖励，以及低层策略的\((s_{t + i}, g_{t}, a_{t + i}, r_{t + i}^{g_{t}}, s_{t + i + 1})\)，对于所有\(0 < i < c\)。

这里，c是实现每个子目标的固定时间范围，\(r^{g_{t}}\)是实现\(g_{t}\)的奖励。这些数据随后用于训练 HRL 智能体的分层策略。然而，如果智能体在c个时间步后没有实现\(g_{t}\)，那么在转换数据中，子目标将被重新标记为从最大化观察到的转换概率的子目标分布中抽取的另一个子目标\(g_{t}'\)。

然后，高层策略将\(g_{t}'\)视为其后见之明中的输出，这与观察到的转换更相关。通过这种方式，HIRO 降低了有效的非平稳性。HIRO 中的子目标通过从原始状态空间中的状态中选择选择性特征来定义。HIRO 在 MuJoCo [97] 连续控制任务上进行评估，结果表明它比标准 RL 和其他一些 HRL 方法表现更好 [25, 99]。 

与 HIRO 同时，Levy 等人 [54] 提出了一种称为分层演员 - 评论家（HAC）的方法，该方法也通过子目标重新标记来解决非平稳性问题。在这个方案中，高层数据中的输出子目标和低层数据中的输入子目标被智能体实际达到的状态事后替换，而不是像 HIRO 中那样基于概率采样新的子目标。这个简单的方案也使得将等级结构扩展到超过两级成为可能。

HAC 在 MuJoCo [97] 连续控制任务上进行评估，结果表明它比标准 RL 和 HIRO 表现更好。此外，作者发现在这些任务上，三级等级结构比两级等级结构表现更好。 封建等级结构也可以

通过使用自然语言指令而非子目标状态来实现。Jiang 等人 [41] 提出了一种名为基于语言的分层抽象（HAL）的方法。他们假设从状态\(s \in S\)到语言指令\(l \in L\)的映射由人类监督者给出，或使用预定义程序生成，作为指令空间L中指令上的概率分布。在此基础上，定义了一个布尔函数\(\Psi: S ×L \to (0,1)\) 。

现在，如果高层策略选择一个指令l，那么所有满足\(\Psi(s, l)=1\)的状态都是该指令的子目标状态。就本文使用的符号而言，语言指令l是一个子任务\(\omega\)，所有满足\(\Psi(s, l)=1\)的状态都属于\(\omega\)的子目标集，即\(g_{\omega}\) 。

语言指令使用循环神经网络 [16] 进行编码，其输出作为输入提供给低层策略。用于训练低层策略的子任务奖励\(r_{\omega}\)是一个二进制奖励，用于奖励达到满足给定指令的状态。HAL 还使用一种称为事后指令重新标记的机制来处理非平稳性。HAL 在与 CLEVR 语言数据集 [42] 集成的 MuJoCo 连续控制域 [100] 中的物体排列任务上进行评估，发现其性能优于标准 RL 和其他一些 HRL 方法 [3, 69]。

3.1.2 策略树方法

Sutton 等人 [93] 引入了选项框架，其中默认的马尔可夫决策过程（MDP）5（称为核心 MDP）通过将一组称为选项的子任务纳入智能体的行动空间进行扩展。原始行动本身被视为单步选项。一个选项\(\omega\)使用元组\((<I_{\omega}, \pi_{\omega}, \beta_{\omega}>)\)定义。\(I_{\omega} \subset S\)是一组状态，在这些状态中选项\(\omega\)可以被启动或有效。\(\beta_{\omega}: S \to [0,1]\)给出了在状态\(s \in S\)中\(\omega\)终止的概率。

\(\pi_{\omega}: S ×A \to [0,1]\)是选项的策略。一个选项可能有也可能没有相关的奖励函数\(r_{\omega}\)。通常假设选项由程序员预先定义。选项的策略\((\pi_{\omega})\)被预定义为初始策略，可以在特定任务的上下文中使用一种称为选项内学习的机制进行微调。选项内学习即使在给出特定选项奖励\(r_{\omega}\)的情况下也使用任务奖励。此外，任何选项\(\omega\)的 Q 值函数，即\(Q_{\omega}(s, a)\)，表示直到主要任务结束的预期累积奖励，而不仅仅是直到选项本身的时间范围（或终止）。

因此，一个选项不是一个独立的子任务单元，而是融入到核心 MDP 中。这限制了学习到的选项转移到其他任务的能力，但从理论上保证了学习到的分层策略的最优性。Sutton 等人 [93] 在网格世界任务上评估了选项框架，发现它比标准 RL 更快地收敛到最优性能。 Dietterich 提出的 MAXQ 值函数分解将核心 MDP 分解为较小的子 MDP 组件。每个子 MDP 与一个子任务相关联，其策略可以与其他子任务分开学习。这是通过将主要的 Q 值函数分解为子任务的单独 Q 值函数来实现的。由于这种分解，任何子任务\(\omega\)的 Q 值，即\(Q_{\omega}(s, a)\)，仅表示直到该子任务的时间范围（或终止）的预期累积奖励。

因此，每个子任务策略可以作为一个独立的单元进行学习。这与选项 [93] 形成对比，在选项中，子任务融入到核心 MDP 中。值分解的好处是，使用 MAXQ 在一个任务上学习到的子任务策略可以很容易地转移到不同的任务或不同的 MAXQ 智能体。将子任务视为独立单元的缺点是分层策略的最优性受到影响。MAXQ 层次结构只是递归最优的，这意味着 MAXQ 可以学习子任务的最优策略，但整体分层策略通常不是最优的。在 MAXQ 中，子任务\(\omega\)的预定义组件是其终止条件\(\beta_{\omega}\)（例如，事件、条件、子目标状态）和奖励函数\(r_{\omega}\)。子任务除了选择其他子任务外，还可以选择原始行动。MAXQ 在网格世界出租车领域进行评估，在该领域它优于标准 Q 学习。 Parr 和 Russell [73] 提出的抽象机器层次结构（HAMs）使用随机有限状态机（FSMs）[13] 来表示子任务。HAMs 由一组随机 FSMs H定义。每个 FSM \(\mathbb{H}_{i} \in{\mathbb{H}}\)使用各种机器状态定义。机器状态与环境状态不同。一个 FSM 由四种类型的机器状态组成：行动、调用、选择和停止。可能有多个相同类型的机器状态。例如，Parr 和 Russell [73] 展示了一个 FSM，其中有两个调用机器状态 ——“靠墙走” 和 “后退”，可以从该 FSM 的选择机器状态中选择。选择机器状态非确定性地选择\(\mathbb{H}_{i}\)的下一个机器状态。可能的选择包括\(\mathbb{H}_{i}\)的各种行动、调用或停止机器状态。一个 Q 表捕获（状态，选择）对的值。选择使用贪婪策略进行。因此，强化学习（具体来说，Q 学习）用于学习在给定当前环境状态下，在选择状态中要做出的最优选择。如果选择了行动机器状态，则它在环境中执行一个原始行动。如果选择了调用机器状态，则它暂停\(\mathbb{H}_{i}\)的执行并启动另一个 FSM（例如\(\mathbb{H}_{j}\) ）的执行。这相当于从一个子任务转移到另一个子任务。如果选择了停止机器状态，则它终止\(\mathbb{H}_{i}\)的执行并将控制权返回给调用\(\mathbb{H}_{i}\)的 FSM。HAMs 是一个有用且详细的框架，用于对领域中的转移动态进行先验知识编程。然而，由于其复杂的结构，HAMs 在 HRL 中没有得到广泛应用。

3.2 与子任务发现统一的学习分层策略（UNI）

本小节回顾在单智能体和单任务设置下，将子任务发现与分层策略学习统一起来的方法。为了使 HRL 智能体能够在特定任务上部署而无需预定义或手工制作的子任务，在学习智能体的分层策略时，同时发现子任务空间\(( \Omega_{hierarchy })\)至关重要。这需要一种统一或端到端的学习方法，该方法使用相同的数据进行子任务发现和学习分层策略，这些数据是在执行给定任务时收集的。这种统一涉及的一些重要问题如下：发现保持分层策略最优性的子任务空间，在发现过程中从头开始学习子任务的各个组件（终止条件、启动条件、子目标等），发现动态数量的子任务等其他问题。 此后讨论的 UNI 方法基于两种类型的 LHP 方法 —— 封建等级结构（第 3.1.1 节）和选项（策略树方法，第 3.1.2 节）。请参考表 2 对这些方法的总结。 表 2 统一子任务发现与分层策略学习的方法（UNI）

3.2.1 策略树的统一学习

本小节讨论的策略树方法在学习分层策略的同时发现选项 [93]。如第 3.1.2 节所述，一个选项是一个子任务，使用三个关键组件表示：启动条件\(I_{\omega}\)、策略\(\pi_{\omega}\)和终止概率函数\(\beta_{\omega}\)。统一选项发现主要涉及学习与每个选项\(\omega\)相关的\(\pi_{\omega}\)和\(\beta_{\omega}\)，同时学习高层任务策略\((\pi_{\Gamma})\) 。启动条件\(I_{\omega}\)也可以学习或设置为全局。这些组件都不是手工制作的。 Daniel 等人 [17] 提出了一种用于统一选项发现的图形模型。在任何时间步t，这个图形模型的观察变量是环境状态\(s_{t}\)和原始行动\(a_{t}\)。隐藏变量是在该时间步活动的选项\(\omega_{t}\)和终止标签\(b_{t}\)（二进制，0 或 1），表示前一个选项\(\omega_{t - 1}\)是否终止\((b_{t}=1)\)或未终止\((b_{t}=0)\) 。该模型由激活策略\(\mu(\omega | s ; \theta_{O})\)组成，该策略使用\(\theta_{0}\)进行参数化，并在当前状态\(s_{t}\)的条件下提供所有选项的概率分布。每个选项\(\omega\)由一个子策略\(\pi(a | s ; \theta_{A}^{\omega})\)和一个终止函数\(\beta(b | s ; \theta_{B}^{\omega})\)组成。所有选项的\(\theta_{A}^{\omega}\)参数集表示为\(\theta_{A}\)。类似地，所有选项的\(\theta_{B}^{\omega}\)参数集表示为\(\theta_{B}\) 。然后，使用期望最大化（EM）[8] 在最大化步骤中使用加权估计来学习参数\({\theta_{O}, \theta_{A}, \theta_{B}}\) 。EM 算法以一组轨迹作为输入，并学习最能解释这些轨迹的参数。这些轨迹是从 HRL 智能体的探索中获得的。在最大化步骤中，每个状态 - 行动\((s, a)\)对根据优势值\(Q(s, a)-V(s)\)进行加权。通过这种方式，选项学习过程纳入了预期的任务奖励。总体而言，在 EM 过程中共同学习激活策略、所有子策略和所有终止函数的参数\({\theta_{O}, \theta_{A}, \theta_{B}}\) 。因此，这是一种统一的 HRL 方法。该方法在具有离散状态 - 行动空间的网格世界导航任务和具有连续状态 - 行动空间的摆锤摆动任务上进行评估。发现它比标准 RL 和其他一些子任务发现方法表现更好 [66, 85]。这种方法的主要限制是选项的数量需要预先定义和固定。 Konidaris 等人 [50] 提出了一种称为技能链接的方法，在学习 HRL 智能体时逐步构建选项。技能链接过程从创建一个选项\(\omega\)开始，其目标集\((g_{\omega})\)包含主要任务的目标状态。学习选项策略\(\pi_{\omega}\)以达到这些子目标。然后学习一个分类器来找到\(\omega\)的启动状态。那些可以在预定义的时间步数内到达\(\omega\)子目标的状态被分类为正，而那些在时间限制内无法到达子目标的状态被分类为负。正状态被添加到启动集\(I_{\omega}\)中。现在，创建另一个选项\(\omega'\)，其目标集\(g_{\omega}\)等于\(I_{\omega}\) 。然后，对\(\omega'\)重复上述分类和策略学习过程，依此类推，创建一个选项（或技能）链。技能链接可以发现灵活数量的选项。作者在弹珠控制领域对其进行评估，发现它优于标准 RL。最近，Bagaria 等人 [4] 使用深度强化学习将技能链接扩展到连续控制。技能链接的主要限制是它仅适用于具有明确目标状态的任务，并且需要在没有选项的情况下进行大量初始探索才能到达目标状态。 在上述所有方法中，智能体在学习的初始阶段无法使用子任务（选项）。这是因为智能体必须首先收集经验轨迹，以用于发现初始的选项集。Bacon 等人 [3] 提出了一个选项框架，该框架可以从学习过程的开始就与整个分层策略一起学习选项。这种方法称为选项评论家（OC）。在 OC 中，固定数量的选项被随机初始化，带有参数化的策略和终止函数。高层策略也被随机初始化。然后，使用从主要任务奖励导出的策略梯度来学习高层策略和所有选项（策略和终止函数）。OC 不使用子目标或特定选项的奖励，并且从理论上保证使用策略梯度学习最优分层策略。在评估中，OC 在 Atari 游戏（如《海魂》、《吃豆人女士》等）中使用深度学习优于标准 RL。在弹珠领域的学习初始阶段，它也比技能链接 [50] 表现更好。OC 的一个限制是它需要预先定义选项的数量。此外，策略梯度严重依赖于主要任务奖励。因此，OC 在稀疏奖励任务上可能表现不佳 [69, 99]。由于其强大的理论基础，OC 已成为统一 HRL 的流行框架。这导致了各种基于 OC 的方法的出现 [46, 48, 78]，这些方法列在表 2 中。 选项评论家（OC）框架需要为基于选项的半马尔可夫决策过程（SMDP）[93] 定制的策略优化算法。这限制了以现成的方式将其他先进的策略优化算法 [34, 82] 用于 HRL。为了解决这个问题，Zhang 等人 [104] 提出将 HRL 层次结构表述为两个并行的增强马尔可夫决策过程（MDPs）[55]，其中每个 MDP 使用增强状态空间，该空间是原始状态空间和选项集的叉积。高层 MDP 对在选项及其相应终止条件上学习策略的问题进行建模，而低层 MDP 对学习选项策略的问题进行建模。两个 MDP 都仅使用任务奖励，不使用子目标或子任务奖励。所提出的方法称为双演员 - 评论家（DAC），因为它应用演员 - 评论家算法来学习两个级别的策略。由于增强的 MDP 表述，DAC 与各种现成的演员 - 评论家算法兼容，用于策略优化。它在各种机器人模拟任务上表现出比 OC 显著更好的性能。然而，与 OC 类似，DAC 需要预先定义选项的数量。 已经观察到，OC 和 DAC 方法在长时间训练后，当每个选项的终止概率变得非常高时，可能会遇到高层策略退化现象 [36, 104]。这导致高层策略几乎在每个时间步都从一个选项切换到另一个选项，并且学习到的选项没有专门针对任何可识别的行为。Harb 等人 [36] 认为，从策略优化的理论角度来看，时间扩展的选项不是必需的，因为最优策略实际上是通过原始行动实现的。为了学习时间扩展的选项，他们引入了一个称为审议成本的正则化项，这是高层策略在切换选项时收到的惩罚。这鼓励高层策略更长时间地保留每个选项，从而在经验上比频繁切换的选项表现更好。审议成本被纳入 OC 框架，但 DAC 的作者将这种成本的集成留作未来的工作。另一种形式的退化可能发生在高层策略在整个任务持续时间内选择单个选项时。这可能是因为如果每个选项使用全局启动条件\(I_{\omega}\)，则它可以在状态空间的任何地方启动。Khetarpal 和 Precup [46] 提出了一种称为兴趣 - 选项 - 评论家（IOC）的方法，该方法基于 OC 框架构建，使用策略梯度学习每个选项的启动条件，以便各种选项可以专门针对不同的行为，从而防止退化。

3.2.2 封建等级结构的统一学习

在封建 UNI 等级结构中，子目标空间和所有级别的通用策略以统一的方式学习。 Vezhnevets 等人 [99] 提出了一种神经网络的封建等级结构，其中一个称为 “管理者” 的高层网络在学习到的潜在子目标空间中采样一个子目标。子目标可以是潜在空间中的一个点，也可以是表示潜在空间中方向的单位向量。子目标作为输入被一个称为 “工作者” 的低层网络接收，工作者必须学习一种策略，使用到子目标的距离作为奖励来实现该子目标。工作者使用从基于子目标的奖励导出的常规策略梯度进行训练。管理者使用作者引入的转换梯度进行训练。这个梯度是使用任务奖励以及分配给工作者的子目标与工作者实际进行的状态转换之间的距离导出的。因此，管理者从任务奖励和工作者的行为中学习。转换梯度用于学习管理者策略和潜在子目标空间。这种称为封建网络（FuN）的方法在 Atari 游戏（如《蒙特祖玛的复仇》）上比 DQN [68] 和选项评论家 [3] 表现更好。 封建网络不能保证学习到的子目标空间导致最优分层策略。Nachum 等人 [70] 在基于 HIRO [69] 开发的子目标表示学习方法中解决了这个问题（HIRO 在第 3.1.1 节中讨论）。作者基于分层策略的次优性理论界限推导出一个优化目标。这个目标用于学习一个函数\(f_{\theta}(s)\)，该函数将状态空间转换为低维子目标空间。因此，学习到的子目标空间表示最小化了次优性，并且基于 HIRO 的分层策略解决了非平稳性问题。该方法在 MuJoCo 连续控制任务 [97] 上进行评估，使用低维状态空间和高维状态空间（例如，用作状态的图像）。它优于各种其他子目标表示方案，如直接使用原始状态（例如，图像）作为子目标、以 FuN [99] 的方式学习潜在空间、使用从变分自动编码器 [47] 导出的子目标嵌入等。

3.3 独立子任务发现（ISD）

本小节回顾在单智能体和单任务设置下独立子任务发现的方法。当目标是自动找到与任务无关且可转移到各种未知任务的 HRL 智能体的子任务时，就会出现 ISD 挑战。这意味着子任务发现过程应该独立于智能体分层策略的学习过程。ISD

方法背后的共同思想与机器学习一般背景下的预训练类似 [22]。在 ISD 方法中，子任务发现通常发生在预训练阶段。然后，发现的子任务用于学习分层策略，以执行特定的目标任务。这种预训练方法导致了 ISD 中的一些关键问题，如下所示：确保子任务发现过程的数据效率，发现能够独立于任何特定任务对状态空间进行多样化探索的子任务，学习连续子任务空间，以便通过在目标任务上采样新子任务实现泛化等其他问题。 需要明确的是，我们并不绝对地将某一方法归类为 ISD，因为其使用的子任务发现算法也有可能通过与智能体分层策略训练同时运行，且使用相同任务数据，从而适用于统一学习。在后续讨论中，只要适用，我们都会提及这一点。请参考表 3 对 ISD 方法的总结。 表 3 独立子任务发现（ISD）的方法

3.3.1 子目标的发现

可以通过发现相应的子目标（第 2.2.1 节提到的目标组件之一），然后学习一个子任务策略来达到一个子目标或一组相关子目标，从而构建一组子任务。 一种直接的子目标发现方法是在任务领域的状态空间中寻找瓶颈。瓶颈是指连接各种初始状态和各种目标状态的多条路径汇聚的状态。移除这些瓶颈可能会切断通往状态空间中可能目标状态的通道。因此，发现的瓶颈被视为重要的子目标，并学习子任务策略以达到它们。 McGovern 和 Barto [64] 提出了一种基于频率的瓶颈发现方法。该方法利用多样密度 [63] 的思想来寻找有趣的瓶颈。智能体使用初始策略探索状态空间，并收集从各种初始状态到各种终端状态的轨迹。根据终端状态是否为期望的目标状态，每个轨迹被分类为正或负。这里，期望的目标状态与预训练任务相关。然后，使用多样密度（DD）度量来估计一个状态出现在正轨迹上的概率与出现在负轨迹上的概率。具有较高 DD 的状态被选为瓶颈子目标。Simsek 和 Barto [84] 也提出了一种基于频率的瓶颈发现方法，该方法可能更具数据效率，因为他们从成功和不成功的经验中构建部分状态 - 行动转移图。在这个图中，每个节点是一个状态，每条边是一个行动。该图可通过简单地沿着各个节点之间的连接来模拟新的轨迹。作者使用一种称为中介中心性的度量，定义为\(\sum_{s ≠t ≠v} \frac{\sigma_{s t}(v)}{\sigma_{s t}} w_{s t}\) ，其中\(\sigma_{s t}\)是从节点s到节点t的最优路径总数，\(\sigma_{s t}(v)\)是通过节点v的此类路径数量，\(w_{s t}\)是\((s, t)\)对的权重。如果节点v的中介中心性得分比其邻居高出一定阈值，则v被选为子目标。 频率统计需要生成大量轨迹来估计各种状态的出现频率。一种更有效的方法是简单地构建一次状态 - 行动转移图，其中每个节点是一个状态，每条边是一个行动，然后通过分析不同子图之间的连通性来寻找瓶颈。Menache 等人 [66] 提出了一种称为 Q - cut 的方法，该方法在全局环境上构建状态 - 行动转移图，然后使用最大流 / 最小割算法 [18] 找到瓶颈节点。每个瓶颈被视为一个子任务的子目标，并学习子任务的策略以达到它。由于需要构建全局图，这需要多样化的探索，所以 Q - cut 不太容易扩展到大型和 / 或连续状态空间。Simsek 和 Barto [85] 提出了一种类似的图割方法来寻找瓶颈，但他们使用局部子图而不是在整个状态空间上构建的全局图。这被称为 L - cut。L - cut 可以增量式地找到局部瓶颈，并且可以应用于大型状态空间，因为智能体不需要构建全局图。然而，它不容易扩展到连续状态空间，因为该算法使用的图需要离散状态作为节点。 瓶颈发现可能不适用于不一定包含可识别瓶颈的任务领域。当通往各种期望目标状态的路径分布多样且没有充分汇聚在特定瓶颈上时，就可能出现这种情况。Machado 等人 [60] 提出了一种寻找分布在状态空间不同区域而非仅在瓶颈处的子目标的方法。该方法使用原型价值函数（PVFs）7 [61]。子目标位于定义在状态空间上的不同 PVFs 的局部最大值处。PVFs 是从状态转移图的拉普拉斯矩阵 8 的特征分解中导出的。Bakker 和 Schmidhuber [5] 提出在状态空间中直接进行无监督聚类，以在不同区域发现子目标。智能体探索状态空间，并使用在线自适应资源分配向量量化（ARAVQ）算法 [57] 对状态进行聚类。各种聚类的中心被用作子目标。探索和聚类过程不依赖于任何特定任务，因此子目标发现与任务无关或独立。作者还提供了一种使用已发现的子目标学习分层策略的算法。在该算法中，子目标构成高层策略的行动空间，高层策略使用任务奖励进行学习。低层由多个策略组成，每个策略可以专门用于达到子目标空间的一个子集，并使用实现子目标的奖励进行学习。学习一个映射函数，将子目标分配给适当的低层策略。还有一个类似于 HIRO [69] 或 HAC [54]（第 3.1.1 节）的子目标重新标记机制，用于处理非平稳性。完整的方法称为子目标到子策略学习的分层分配（HASSLE）。 到目前为止回顾的所有子目标发现方法的一个显著限制是发现的子目标空间是离散的。在这样的离散空间中，无法对新子目标进行插值，从而限制了使用发现的子目标空间可以执行的任务范围（或多样性）。发现连续子目标空间对于解决这个问题很重要。Sukhbaatar 等人 [88] 提出了一种称为分层自博弈（HSP）的方法，通过非对称自博弈 [89] 学习子目标的连续嵌入。非对称自博弈是一个无监督的预训练阶段，如下所示：在非对称自博弈开始时，初始化两个标准（非分层）RL 策略，例如 Alice（\(\pi_{A}\)）和 Bob（\(\pi_{B}\)）。设初始状态为\(s_{0}\) 。首先，Alice 从\(s_{0}\)开始在环境中采取\(T_{A}\)步。设\(s^{*}=s_{T_{A}}^{A}\)是 Alice 到达的最终状态。接下来，环境重置为\(s_{0}\) ，并将\(s^{*}\)作为目标提供给 Bob。在每个时间步，\(s^{*}\)使用学习到的编码器E编码为低维潜在子目标嵌入，即\(g_{t}=E(s_{t}^{B}, s^{*})\) ，其中\(s_{t}^{B}\)是 Bob 执行时的时间t的状态。Bob 策略选择原始行动为\(a_{t}^{B}=\pi_{B}(s_{t}^{B}, g_{t})\) 。Bob 有\(T_{B}\)步来实现目标状态\(s^{*}\) ，否则失败。如果达到目标，Bob 获得奖励\(R^{B}=1\) ，否则为 0。Alice 获得奖励\(R_{A}=1 - R_{B}\) 。作者选择\(T_{B} \sim T_{A}\) 。这导致了一种非对称自博弈机制，其中 Bob 学习达到 Alice 设置的目标，而 Alice 学习实现超出 Bob 能力范围的新的、未探索的目标。通过这种方式，由这两个策略组成的智能体在没有外部监督的情况下有效地探索环境。 HSP 的子目标编码器\(E(s_{t}^{B}, s^{*})\)基本上将各种目标状态\((s)\)编码到低维子目标空间中。一旦在非对称自博弈的预训练阶段发现了子目标空间，它就简单地用作执行特定任务的 HRL 智能体高层策略的连续行动空间。智能体的低层使用 Bob 策略初始化，然后在任务上进行微调。

3.3.2 多样化技能的发现

子目标发现方法不适合寻找没有明确相关子目标的子任务。考虑一个子任务示例 “在交通中驾驶”，这是到达目的地的较长时域任务的一部分。这个子任务要求智能体在没有任何特定子目标的情况下在交通中操纵车辆。子目标发现不适合找到这样的子任务。因此，需要通用的方法，能够直接发现一组多样化的技能，而不是通过子目标来学习它们。如第 2.3 节所定义，“技能” 在语义上指的是子任务的策略，代表了做好某件事情的能力。发现后，技能可以作为低层策略添加到 HRL 智能体中，并在特定任务上进行微调。 一种发现多样化技能的策略是最大化技能\(\omega\)与使用该技能到达的状态或生成的轨迹之间的互信息（MI ）9。这是通过使用潜在技能向量（例如\(z_{\omega}\) ）并将技能策略定义为\(\pi_{\omega}(s)=\pi(s, z_{\omega})\)来实现的，其中\(\pi(s, z_{\omega})\)是一个通用策略，将技能向量作为输入。在大多数此类方法中，\(z_{\omega}\)通常是一个独热编码向量 [1, 24, 25, 31]。最大化\(z_{\omega}\)与遵循\(\pi(s, z_{\omega})\)到达的状态或生成的轨迹之间的MI ，会导致发现一组与不同终端状态或轨迹相关的多样化技能。下面概述基于这种策略的具体方法。 Florensa 等人 [25] 提出了一种称为 SSN4HRL 的方法，其中通用策略\(\pi(s, z_{\omega})\)由随机神经网络 [98] 表示。该策略通过最大化MI奖励\(P(z_{\omega} |(x, y))\)来学习，其中\((x, y)\)是智能体在空间环境中的位置，\(P(z_{\omega} |(x, y))\)是通过观察\((x, y)\)预测\(z_{\omega}\)的概率。只有当执行不同技能到达的位置足够不同时，这个概率才能最大化。Gregor 等人 [31] 提出了变分内在控制（VIC），通过最大化包含技能向量\(z_{\omega}\)与策略\(\pi(s, z_{\omega})\)到达的终端状态\(S_{T}\)之间的MI项\(P(z_{\omega} | s_{0}, s_{T})\)（在起始状态\(S_{0}\)的条件下）的目标来发现技能。Eysenbach 等人 [24] 提出了一种称为 “多样性就是你所需要的一切”（DIAYN）的方法，通过优化一个目标函数来发现技能，该目标函数旨在最大化技能向量\(z_{\omega}\)与\(\pi(s, z_{\omega})\)生成的轨迹中的每个状态之间的MI ，而不考虑状态在轨迹中的顺序。 所有这些方法都可以发现一组多样化的技能，但也有一些共同的局限性，例如它们只能发现预定义数量的技能，并且它们的MI目标要么忽略轨迹，要么不考虑轨迹中状态的顺序。为了解决这些局限性，Achiam 等人 [1] 提出了通过强化学习进行选项的变分自动编码学习（VALOR）。在这种方法中，策略\(\pi(s, z_{\omega})\)基本上是一个将\(z_{\omega}\)编码为轨迹的编码器。轨迹表示为\(\tau\) 。它被输入到一个解码器中，解码器必须将其映射回\(z_{\omega}\) 。这导致了一个旨在最大化\(P(z_{\omega} | \tau)\)的优化目标。因此，VALOR 发现了一组本质上与智能体采取的各种轨迹相关的多样化技能。VALOR 还提供了一种逐步发现越来越多技能的过程。 到目前为止讨论的 ISD 方法只能发现离散的技能集。一个可能的原因是，在估计MI时，计算连续技能空间上的概率分布很复杂。然而，发现连续的技能空间对于泛化很重要，这样可以在这样的连续空间中轻松插值新的技能。Co - Reyes 等人 [77] 提出了一种称为自一致轨迹自动编码器（SeCTAR）的方法，其中一个编码器 LSTM [40] 将状态转换轨迹（即\({s_{t}, s_{t + 1}, s_{t + 2} \cdots}\)）嵌入到低维连续潜在向量空间中，一个解码器 LSTM 学习将潜在向量解码为策略。一个潜在向量代表相似的轨迹，因此从潜在向量解码的策略被认为代表一种技能。通过使用生成多样化轨迹的探索机制来学习多样化的潜在空间。这个编码器 - 解码器模型在预训练阶段用于技能发现。预训练阶段之后，编码器模块被移除，编码的潜在空间作为连续的技能空间可用。HRL 智能体的高层策略在这个连续空间中采样一个技能，然后由解码器模块以策略的形式解码。除了独立的技能发现，作者还将 SeCTAR 扩展用于在特定任务上的统一学习。这是通过一个探索器策略实现的，该策略探索与任务相关的状态及其邻域，使得 SeCTAR 编码器模块编码的轨迹与给定任务相关。通过这种方式，发现的技能空间与 HRL 智能体同时训练的任务相关。 Hausman 等人 [38] 提出了一种变分推理方法，用于学习多样化的技能以及技能的连续潜在嵌入。用于学习的目标是最小化基于独热技能向量的潜在嵌入分布与基于执行该技能生成的轨迹的潜在嵌入分布之间的交叉熵 10。学习到的潜在嵌入是连续的技能空间，在其中可以插值新的技能。

3.4 使用 HRL 的迁移学习（TransferHRL）

本小节回顾通过多任务或迁移学习在多个任务上学习单个 HRL 智能体的方法。TransferHRL 类别代表了所有这些有或没有子任务发现的方法。HRL 迁移学习的概念源于这样一种想法，即某些子任务在多个相关任务中是可共享的。在一个任务的上下文中学习执行子任务的策略也可以用于加速智能体在其他相关任务上的适应。因此，这是 HRL 中需要解决的一个重要挑战。 在 RL 的背景下，迁移学习通过将经验数据、行动策略或 Q 值函数从一个任务转移到另一个任务来加速后者的学习 [55, 81]。在 HRL 的背景下，转移主要任务策略（分层策略中的最高层）的问题可以使用 RL 转移方法来解决。然而，子任务成为额外的可转移组件，包括它们的策略、终止 / 启动条件、子目标等。与标准 RL 的迁移学习相比，这给使用 HRL 的迁移学习（TransferHRL）带来了一些独特的问题。TransferHRL 特有的一些问题如下：

• 在终身迁移学习中有效扩展到大量子任务。
• 在具有不同状态空间的任务域之间转移子任务。
• 在多个相关任务上从头开始学习子任务。 本小节将讨论这些问题以及解决它们的相应方法。我们重申，ISD 方法（第 3.3 节）学习与任务无关的子任务，可以转移到各种任务。然而，ISD 方法没有解决上述问题。

3.4.1 迁移 + 子任务策略蒸馏

HRL 智能体在从一个任务转移到另一个任务（如在终身学习 [15] 期间）时，可能会学习并积累大量子任务策略。天真地将大量子任务添加到高层策略的行动空间中，由于需要存储多个子任务策略，可能会导致内存效率低下。Tessler 等人 [96] 提出了一个深度 HRL 框架，称为分层深度强化学习网络（H - DRLN），用于以内存高效的方式转移和保留一组针对各种子任务的预训练策略（无子任务发现）。这些策略是使用手动定义的目标进行预训练的。通过作者引入的多技能蒸馏，这些策略被转移到 HRL 智能体（在目标任务中）。多技能蒸馏是一种策略蒸馏 [81] 形式，使 H - DRLN 能够有效地将几个子任务的策略组合成一个单一的蒸馏策略。这使得 H - DRLN 在内存方面高效。在执行目标任务时，H - DRLN 智能体使用高层策略选择一个由蒸馏策略（在低层）执行的子任务。H - DRLN 在 Minecraft 游戏 11 中学习执行多个任务，与标准 RL 相比，具有更低的样本复杂度和更好的性能。H - DRLN 的主要限制是子任务的策略需要在蒸馏之前使用手动定义的目标进行预训练。此外，H - DRLN 能够将现有策略蒸馏到目标策略中，但没有提供持续发现新子任务的方法。

3.4.2 迁移 + 智能体空间子任务

在特定任务域中学习的子任务策略是基于该特定域的状态空间S的。如果该策略转移到一个新的任务域，其状态空间与S不同，那么该策略可能不再是最优的。为了解决这个问题，需要实现域不变转移，使得子任务策略对变化的状态空间具有鲁棒性。Konidaris 等人 [49] 提出了一种学习可以转移到具有不同状态空间的各种任务的选项的方法。选项是如第 3.1.2 节所定义的子任务表示。通过使用两个单独的状态表示 —— 一个在任务空间中，另一个在智能体空间中，来实现不变性。智能体空间表示包含依赖于智能体且在各种任务中不变的特征。选项策略在智能体空间中学习，只要智能体空间在这些任务中保持相同，它们就可以转移到具有不同任务空间的各种任务中。

选择执行选项的高层策略则使用任务空间进行学习，并根据当前任务进行调整。作者设计了多个自己的任务领域版本来评估该方法。结果发现，引入智能体空间选项相较于常规基于选项的技术，提升了智能体的性能。该方法的主要局限在于，选项并非自动发现的，因为其策略是通过预定义奖励学习得到的，而且智能体空间与任务空间的区分需要手动定义。

3.4.3 迁移 + 子任务的元学习

除了高效转移预训练的子任务外，在多个任务中从头发现子任务也很重要。Frans 等人 [29] 提出了一种深度 HRL 方法，通过在多个相关任务上进行元学习来发现选项。这种方法称为元学习共享层次结构（MLSH），它包含一组在不同任务间共享参数的选项，这些选项通过联合最大化在所有任务中获得的预期奖励（元学习）从头开始学习。MLSH 不使用任何其他手工制作的奖励或子目标。学习到的选项通过特定任务的高层策略转移到未见过的任务中。MLSH 在 MuJoCo [97] 运动控制领域进行评估，结果优于标准 RL 和选项评论家（Option-Critic）[3]。MLSH 的主要局限在于选项的数量需要固定，这限制了使用 MLSH 可以执行的任务的多样性。简单增加选项数量会使智能体需要存储和学习大量的选项策略，在内存和计算方面可能效率较低。

3.5 多智能体分层强化学习（MAHRL）

本小节回顾在单个联合任务上学习协调多个 HRL 智能体的方法。MAHRL 类别代表了所有这些有或没有子任务发现的方法。在标准多智能体强化学习（MARL）[26, 27, 59, 94] 中，多个智能体通过优化联合任务目标，偶尔还通过共享关于它们状态和行动的共同信息，来学习协调它们的原始行动策略。超越标准 MARL，任务分解的好处也可以用于多智能体协调，将联合任务划分为分布在不同 HRL 智能体上的多个子任务。每个智能体可以执行多个子任务，并且不同智能体学习协调它们选择子任务的高层策略，而不仅仅是原始行动策略。在某些情况下，智能体可能只在高层进行协调，而将它们的原始行动策略视为相互独立 [58]。学习在 HRL 智能体之间进行协调被称为多智能体 HRL（MAHRL）[30]。 开发 MAHRL 智能体是一个具有挑战性的任务，因为涉及不同的复杂问题。标准 MARL 中存在的所有常见问题也适用于 MAHRL，例如由于多个智能体同时学习导致的非平稳性、由于有限通信导致的部分可观测性，以及在异构智能体情况下奖励分配的困难。然而，使用分层策略（对于所有智能体）也引入了一些 MAHRL 特有的额外问题，描述如下：

• 不同智能体间子任务终止的同步。不同智能体做出的决策的同步受到它们子任务的终止（即\(\beta_{\omega}\)）的影响 [79]。可以通过在任何一个智能体的子任务终止时强制终止所有智能体的子任务，或者引入等待时间直到所有子任务自然终止，来同步所有智能体的子任务终止。这种方案使决策协调变得容易，但也对终止条件施加了强制偏差，这可能导致次优行为。另一种方案是异步终止，其中每个智能体的子任务独立于其他智能体的子任务终止。这种方案没有任何强制中断，但由于决策异步发生，使得决策协调变得困难。
• 在其他智能体行为背景下的子任务发现。智能体在子任务发现过程中必须考虑环境中其他智能体的存在。由于其他智能体是智能体环境中的非平稳元素，发现的子任务空间本身可能变得非平稳。这也使得独立子任务发现（ISD）极具挑战性，因为一个智能体发现的子任务的适用性不仅取决于目标任务的动态，还取决于目标任务中存在的其他智能体。

定义关键术语和概念

本小节在 HRL 背景下使用的一些重要术语和概念定义如下。

• 集中式智能体意味着一种范式，其中所有智能体使用单个中央策略（例如中央管理器策略 [2]）共享它们分层策略的最高层。
• 具有集中式学习的分散式智能体意味着一种范式，其中所有智能体都有自己独立的分层策略（没有中央策略），但它们通过集中式信息共享（或通信）进行学习。信息通常包括状态观察和不同智能体正在执行的子任务。
• 完全分散式智能体意味着一种范式，其中所有智能体都有分散式分层策略，并且在部分可观测性下学习，无需信息共享或中央策略。
• 同质智能体是指那些具有相似子任务空间和分层结构的智能体。这意味着每个智能体可能有能力独立执行任务，并且不同智能体之间可能没有显著的相互依赖关系。
• 异质智能体是指那些具有不同子任务空间和分层结构的智能体。因此，它们在能力上有所不同，单个智能体可能无法独自执行整个任务。这些智能体可能有很强的相互依赖关系，例如一个智能体协助另一个智能体，或者除非另一个智能体完成其子任务，否则一个智能体不可能获得任务奖励。 随后将讨论关键的 MAHRL 方法。请参考表 4 对这些方法的总结。 表 4 多智能体分层强化学习（MAHRL）的方法

3.5.1 学习多智能体分层策略

Ghavamzadeh 等人 [30] 提出了一种在不同任务分解层次上的同质智能体之间进行合作的方法。这种方法称为合作 HRL。作者使用 MAXQ 来定义和学习每个智能体的分层策略。该方法是在 Makar 等人 [62] 早期工作的基础上开发的。每个智能体的子任务空间是预定义的，为每个子任务手工制作奖励函数。每个智能体的任务分解层次结构可能由两个以上的级别组成，并且每个级别可以定义为合作或独立级别。智能体在子任务方面进行合作。原始行动级别对所有智能体都是独立的。此外，不同智能体的子任务使用预定义的异步事件终止。这种方法使用具有集中式学习的分散式智能体范式。所有智能体都是同质的，它们通过共享关于它们局部状态和所选子任务的信息来学习它们的分散式分层策略。作者报告称，在仓库管理的自动导引车（AGV）任务和垃圾收集任务中，合作 HRL 比标准 MARL 表现更好。为了减轻持续信息共享的要求，作者还提出了该方法的一个变体，在每个智能体层次结构的更高级别进行通信和非通信决策。 合作 HRL 解决了通常没有强相互依赖关系的同质智能体之间的协调和通信问题。然而，这种方法在异质环境中应用并不容易，在异质环境中，各种智能体执行任务的不同部分，通常有很强的相互依赖关系，例如一些智能体可以到达奖励状态，而其他智能体则起到辅助作用，使这些智能体能够到达奖励状态。这意味着对于某些智能体来说，任务奖励可能过于稀疏或延迟，使得学习过程变得困难。在复杂领域中设计智能体特定的奖励可能具有挑战性。合作 HRL 的另一个局限是它使用需要为所有子任务手动指定的终止事件。 Pateria 等人 [74] 提出了一种基于选项 [93] 的方法来解决上述两个问题。这种方法称为基于子任务赋能的多智能体选项（ISEMO）。它利用异质智能体之间的相互依赖关系来推导称为子任务赋能奖励（ISER）的内部奖励。相互依赖关系基于不同智能体之间各种子任务的预定义启动条件。当一个智能体通过创造满足另一个智能体子任务启动条件的环境条件来赋能另一个智能体时，ISER 作为正奖励给予该智能体。ISER 被添加到智能体观察到的（外部）任务奖励中，从而增强了任务奖励。因此，即使特定智能体的任务奖励很稀疏，它仍然可以使用 ISER 来学习对其他智能体有帮助的行为。此外，ISEMO 借鉴选项评论家（Option-Critic）[3] 的思路，使用基于梯度的方法学习每个子任务的终止函数。学习到的终止是异步的。作者在一个包含异质和同质智能体混合的搜索与救援任务中，将 ISEMO 与合作 HRL 方法进行比较。发现由于 ISER 和学习到的终止，ISEMO 比合作 HRL 表现更好。ISEMO 和合作 HRL 的一个相似之处在于，ISEMO 也使用具有集中式学习的分散式智能体范式，其中智能体共享它们的局部状态和所选子任务的信息。ISEMO 的主要局限是需要手动定义各种子任务的启动条件来生成 ISER。此外，ISEMO 只学习子任务的终止函数，但需要预定义子任务的策略。 Tang 等人 [95] 提出了一种具有预定义子任务（使用手工制作的子任务奖励定义）的 MAHRL 深度学习方法。他们通过将深度 MARL 方法（如 QMIX [76] 和 CommNet [90]）应用于 MAHRL，使用具有集中式学习的分散式智能体。还提出了不同子任务同步和异步终止的不同方案。该方法在修改后的垃圾收集任务 [30] 和一个在线手机游戏上进行评估。结果发现它优于标准 MARL 和独立学习的 HRL 智能体。然而，它仅适用于同质智能体。 到目前为止讨论的方法适用于具有集中式学习的分散式智能体。另一种方法是学习在最高层具有共同中央策略的集中式智能体。Ahilan 等人 [2] 提出了一种深度 MAHRL 方法，其中中央管理器策略同时为一组工作者选择子任务。子任务使用子目标预定义。这是一个封建等级结构，其中每个工作者策略是一个通用策略。每个工作者策略属于一个单独的智能体。只有中央管理器接收任务奖励，而工作者使用实现子目标的奖励进行学习。这种方法称为封建多智能体层次结构（FMH）。工作者可以是同质的或异质的。不同工作者执行的不同子任务的终止由管理器同步。FMH 在多智能体粒子环境 13 中的合作通信和导航任务上进行评估，发现它优于标准 MARL。 到目前为止讨论的方法都假设不同智能体之间可以通过通信或使用中央策略来共享信息。一个更具挑战性但更现实的范式是学习协调完全分散式智能体。这个范式在训练或执行期间不假设通信或集中化的可用性。因此，智能体需要在部分可观测性下学习 [44]。Omidshafiei 等人 [72] 引入了一个使用子任务（宏观行动）进行分散式多智能体协调的理论框架，称为分散式部分可观测半马尔可夫 MDP（Dec-POSMDPs）。Liu 等人 [58] 提供了一种基于 Dec-POSMDPs 的 MAHRL 方法。在这种方法中，所有智能体的子任务都是预定义的，并且假设智能体从专家演示中获得了一组包含子任务序列的高级轨迹。然后，使用作者开发的一种称为基于策略的期望最大化（PoEM）的算法来学习分散式智能体的策略层次结构。所有策略都将状态转换的历史作为输入，以解决部分可观测性问题。PoEM 在多智能体推箱任务上进行评估，发现它优于动态规划方法。它适用于同质或异质智能体。子任务的终止可以是异步的。然而，这种方法的一个关键局限是需要预先提供演示轨迹。

3.5.2 与子任务发现统一的学习多智能体分层策略

Yang 等人 [101] 提出了一种基于变分推断 [1]（第 3.3.2 节）的具有技能 14 发现的 MAHRL 方法。这种方法称为分层技能发现（HSD）。其范式是具有集中式学习的分散式智能体，其中智能体是同质的。HSD 使用 QMIX [76] 进行集中式学习。在 HSD 中，每个智能体使用由两个级别组成的分散式封建等级结构。它使用其高层策略选择一个独热编码的技能向量。低层通用策略将这个技能向量作为输入并生成轨迹。这个通用策略通过最大化各种输入技能向量与相应轨迹之间的互信息（MI）来学习，从而发现多样化的技能。然而，智能体还必须使技能发现与和其他智能体的协调保持一致。因此，HSD 将任务奖励添加到低层通用策略的 MI 目标中，这样学习到的技能不仅多样化，而且与多智能体任务目标相关。每个智能体的高层策略仅使用任务奖励进行学习。不同智能体的技能在固定时间步后同步终止。HSD 在 STS2 模拟器中的足球游戏上进行评估 15。它比标准 MARL 和独立训练的 HRL 智能体表现更好。作者还报告了一些可识别的发现技能，例如进攻移动、防守移动、射门等。他们还发现，仅使用 MI 目标而不添加任务奖励发现的技能不会带来良好的性能。这表明发现的技能不能与任务无关。HSD 的主要局限是技能 / 子任务的数量必须预先定义和固定。没有提供增加这个数量或学习大量技能空间的技术。 Chakravorty 等人 [14] 提出了一种 MAHRL 方法，将单智能体选项评论家（Option-Critic）框架 [3] 扩展到多智能体协调。这种方法称为分布式选项评论家（DOC）。他们为所有智能体使用单个中央高层策略（因此是集中式智能体范式）。低层选项策略是分散式的。智能体还有一个学习到的广播函数，用于与中央高层策略共享局部信息。高层策略、低层选项策略和选项终止函数仅使用从任务奖励导出的策略梯度进行学习。学习到的终止是异步的。作者在简单的网格世界任务上评估 DOC，发现它与标准 MARL 相比具有竞争力。

3.6 方法综述的关键要点

通过对本节中广泛的 HRL 方法的综述，我们旨在提供关于 HRL 研究的广泛进展和当前状态的重要见解。在这方面，随后讨论从所综述的方法中得出的一些关键要点。

• 学习分层策略没有统一的框架 —— 不同的方法应根据不同的需求选用。学习分层策略的两类方法提供了不同但重要的好处。封建等级结构方法使用子目标（或指令）来表示各种可能的子任务 [19, 41, 51, 69]。这类方法有扩展子任务空间的空间，可以通过使用大量子目标或低维连续子目标空间来实现。这种扩展也是可能的，因为每个级别都使用通用策略，这意味着大量子任务不需要学习和存储许多单独的策略，不像策略树方法。
• 然而，策略树方法 [73, 93] 不像封建方法那样局限于仅学习基于子目标（或基于指令 [41]）的子任务。不同的子任务策略可以代表不同类型的行为，例如基于子目标的、基于轨迹的（例如 “绕圈移动”）、通用技能（例如 “在交通中驾驶”）等等。总之，不同的方法提供不同的好处，但没有一个统一的框架涵盖所有方面。
• 子任务发现可使用多种原则。对于发现的子任务的质量没有单一的标准。HRL 研究人员对于子任务发现所使用的原则有多种想法 —— 划分状态 - 行动转移图 [66, 85]、聚类 [5]、多样化探索 [60, 88]、变分推断 [1] 等等。这些原则大多基于与任务奖励最大化目标不同的目标。因此，从理论上无法保证发现的子任务的最优性。一些 UNI 方法 [3, 70, 99] 表明，任务奖励本身也可用于子任务发现。但是，即使在这些方法中，将奖励纳入子任务发现过程的方式也各不相同，例如使用策略梯度 [3, 99]、使用次优性目标 [70] 等等。因此，目前还没有标准的子任务发现原则。读者必须根据所需的特征来评估特定的方法。
• 大规模技能发现方向可能会出现新趋势。近年来，强化学习社区对连续控制和机器人操作问题表现出越来越浓厚的兴趣 [32, 35]。受此影响，HRL 研究也开始产生用于发现机器人技能 [1, 77] 和学习连续控制分层策略 [54, 69, 102] 的方法。在不久的将来，这一趋势可能会持续下去，特别是在大规模获取机器人连续控制技能方面，例如 “跳跃”、“奔跑”、“移动物体”、“在交通中驾驶”、“停车” 等等，在各种任务领域 [83]，以及将 UNI 方法应用于端到端学习大量此类技能。这一趋势很重要，因为多样化的机器人技能对于 HRL 的各种实际应用（如仓库管理、手术机器人、自动驾驶等）是必要的。

4 未来研究的开放性问题

HRL 在强化学习社区中受到越来越多的关注。然而，关于 HRL 的可扩展性、效率和理论稳健性仍然存在不同的开放性问题。随后讨论其中一些开放性问题，旨在确定未来研究的更广泛方向。本讨论排除了增量问题和任何特定方法的扩展。

• 构建可转移技能的终身知识库。人类在一生中学习各种技能，这些技能作为有价值的知识被保留下来，并在不同场景中选择性地应用。对于实现能够在其生命周期中持续学习、保留和重用广泛技能的通用 HRL 智能体来说，同样的能力至关重要。构建技能的终身知识库需要整合多种操作，例如技能发现、技能转移以及使用相关技能作为子任务进行分层学习以执行新任务。目前，这些必要的操作由不同的方法提供，特别是用于无监督技能发现 [1, 38, 83]、技能转移 [29, 96]、技能组合 [6]、技能重用 [37] 以及在训练 HRL 智能体时选择性启动技能 [45]。需要进一步的研究和开发来设计一个集成的 HRL 框架，将这些操作整体结合起来，以维护可转移技能的终身知识库。
• 利用高级规划改进学习和适应性。用基于模型的规划取代 HRL

  智能体的无模型高层策略，利用学习到的子任务到子任务（或子目标到子目标）的转移动态，有可能加速智能体在长时任务上的学习，并使其更好地适应具有共享动态的新任务 [23, 86]。Zahavy 等人 [103] 提出了一种通过使用一组子奖励分解任务奖励，将高级规划与 HRL 相结合的方法。该方法假设子奖励是预先定义的，为收集每个子奖励定义了一个子任务策略。高级规划启发式算法通过解决旅行商问题 [11] 来找到子任务的最优序列。Sohn 等人 [86] 提出了神经子任务图求解器（NSGS）用于规划。该方法使用一个子任务图，其中子任务、它们的前置条件以及相互依赖关系都是预先定义的。高级规划器是一个图求解器，在子任务图上进行规划。该图可用于以零样本的方式推广到新任务。上述两种方法的共同局限在于，子任务和 / 或它们的相互依赖关系需要手工制作。Eysenbach 等人 [23] 提出了一种名为搜索回放缓冲区（SoRB）的方法，该方法自动从经验回放缓冲区 16 中提取子目标状态，并在这些状态上构建一个图。在这个图中，每个节点是一个状态，一对节点之间的转移边的权重等于使用学习到的 Q 值函数估计的节点之间的距离。高级规划启发式算法在图中找到子目标之间的最短路径以达到目标。通过强化学习训练的低级原始动作策略来遍历该路径。虽然 SoRB 相较于无模型强化学习表现出性能提升，但它要求在构建用于规划的高级图之前先训练原始动作策略。因此，SoRB 不是端到端统一的，并且它仅解决了在学习了先前目标导向任务的原始动作策略和高级图之后，在新的目标导向任务上快速适应的问题。
  总而言之，在将高级规划与 HRL 集成时需要考虑多个方面。自动发现子任务至关重要，还需要进一步研究如何自动学习子任务之间的相互依赖关系，而不是手工制作它们。此外，还应开发新的方法，实现高级规划和低级策略学习的端到端统一。

• 为 HRL 提供理论支持。在许多长时任务领域中，HRL 相较于标准 RL 在实践（或经验）上具有明显的优势 [3, 51, 54, 69, 99]。然而，从理论上讲，仅从 Q 值最大化的角度来看，使用分层策略并没有优势。标准强化学习，尤其是 Q 学习 [100]，从理论上保证仅使用原始动作策略就能收敛到期望的最大 Q 值 [65]。HRL 在经验上的大多数性能优势可能仅仅是由于改进了探索 [43, 71]。不过，Nachum 等人 [71] 也表明，一个复杂的非分层探索方案与标准 RL 智能体相结合，可能会提供与 HRL 智能体相当的性能。因此，需要进行更多的理论研究来支持 HRL 在经验上的优势，并确定在哪些问题领域中 HRL 在最优性能方面具有明显优势。

• 5 结论

  本综述全面概述了分层强化学习（HRL）领域迄今为止的研究，涵盖了从经典方法到最新进展的内容。我们设计了一种新颖且通用的分类法，根据 HRL 方法所解决的关键挑战，将其分为五大类：（i）学习分层策略（LHP），（ii）与子任务发现统一的学习分层策略（UNI），（iii）独立子任务发现（ISD），（iv）使用 HRL 的迁移学习（TransferHRL），以及（v）多智能体 HRL（MAHRL）。我们还根据具体方法对这些方法进行了进一步分类。通过本综述，我们发现，在解决 HRL 的两个主要子问题 —— 如何学习分层策略以及如何自动发现子任务（如 HRL 问题陈述（第 2.2.3 节）中所述）方面，已经取得了显著进展。目前，该领域在使用 HRL 进行迁移学习和多智能体学习方面正在取得进展，在这些方面可能会出现新的趋势，特别是在子任务发现方面。
  尽管取得了这些显著进展，但 HRL 仍有进一步发展的空间，以促进其作为一种可扩展且稳健的范式被更广泛地接受。在这方面，我们确定了一组重要的开放性问题，以推动未来的研究和发展。这些选定的问题涉及：（i）为可扩展的 HRL 进行终身技能发现和利用，（ii）通过利用高级规划提高数据效率，以及（iii）为 HRL 方法提供更多关于最优性的理论保证。