四、不确定性推理方法

写在前面

现实世界中由于客观上存在的随机性，模糊性，反映到知识以及由观察所得到的证据上来，就分别形成了不确定性的知识及不确定性的证据。因而还必须对不确定性知识的表示及推理进行研究。这就是下面需要讨论的不确定性推理。

下面首先讨论不确定性推理中的基本问题，然后着重介绍基于概率论的有关理论发展起来的不确定性推理方法，主要介绍可信度方法、证据理论，最后介绍目前在专家系统、信息处理、自动控制等领域广泛应用的依据模糊理论发展起来的模糊推理方法。

4.1 不确定性推理的基本概念

推理：从已知事实（证据）出发，通过运用相关知识逐步推出结论或者证明某个假设成立或不成立的思维过程。
不确定性推理：从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。

4.1.1.不确定性的表示与量度

（1）知识不确定性的表示（在专家系统中知识的不确定性一般是由领域专家给出的，通常是一个数值——知识的静态强度）
（2）证据不确定性的表示——证据的动态强度（ 用户在求解问题时提供的初始证据。
在推理中用前面推出的结论作为当前推理的证据。）
（3）不确定性的量度
① 能充分表达相应知识及证据不确定性的程度。
② 度量范围的指定便于领域专家及用户对不确定性的估计。
③ 便于对不确定性的传递进行计算，而且对结论算出的不确定性量度不能超出量度规定的范围。
④ 度量的确定应当是直观的，同时应有相应的理论依据。

4.1.2. 不确定性匹配算法及阈值的选择

• 不确定性匹配算法：用来计算匹配双方相似程度的算法。
• 阈值：用来指出相似的“限度”。

4.1.3. 组合证据不确定性的算法:

• 最大最小方法、Hamacher方法、概率方法、有界方法、Einstein方法等。

4.1.4. 不确定性的传递算法

1. 在每一步推理中，如何把证据及知识的不确定性传递给结论。
2. 在多步推理中，如何把初始证据的不确定性传递给最终结论。

4.1.5. 结论不确定性的合成

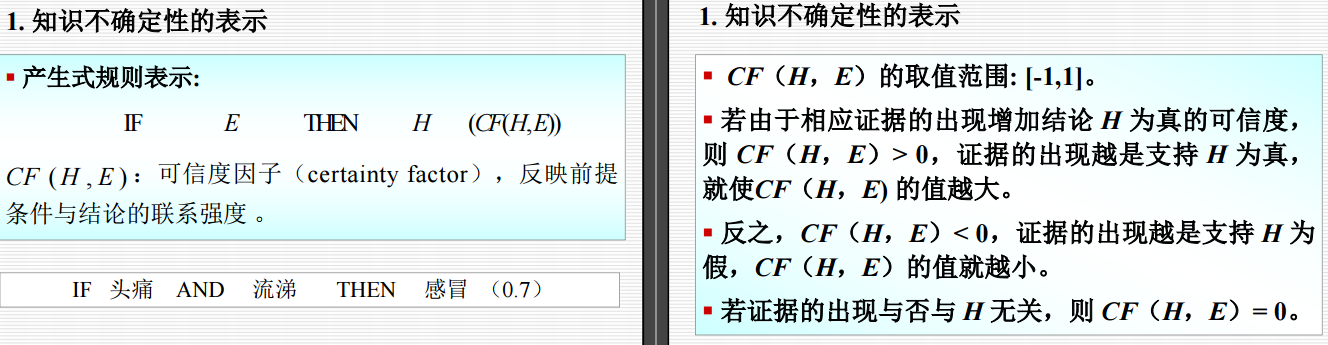
4.2 可信度方法

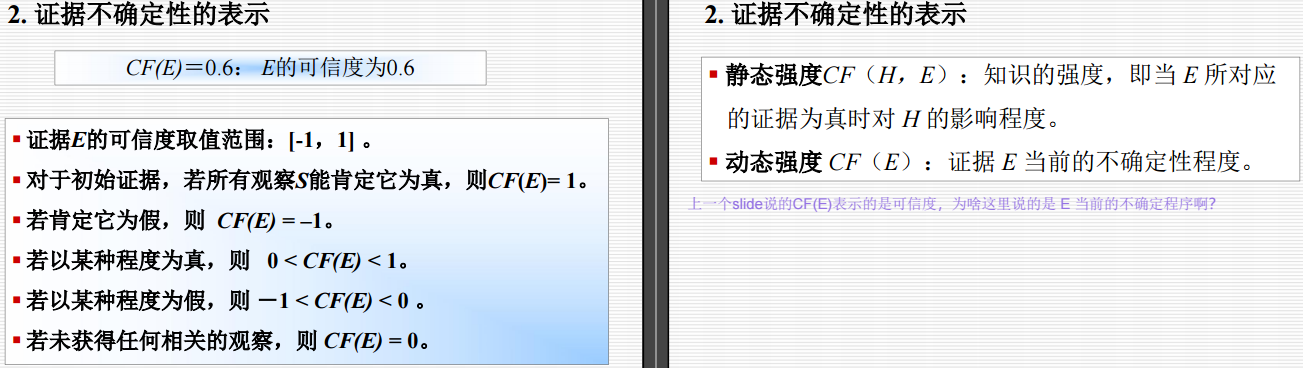
4.3 证据理论

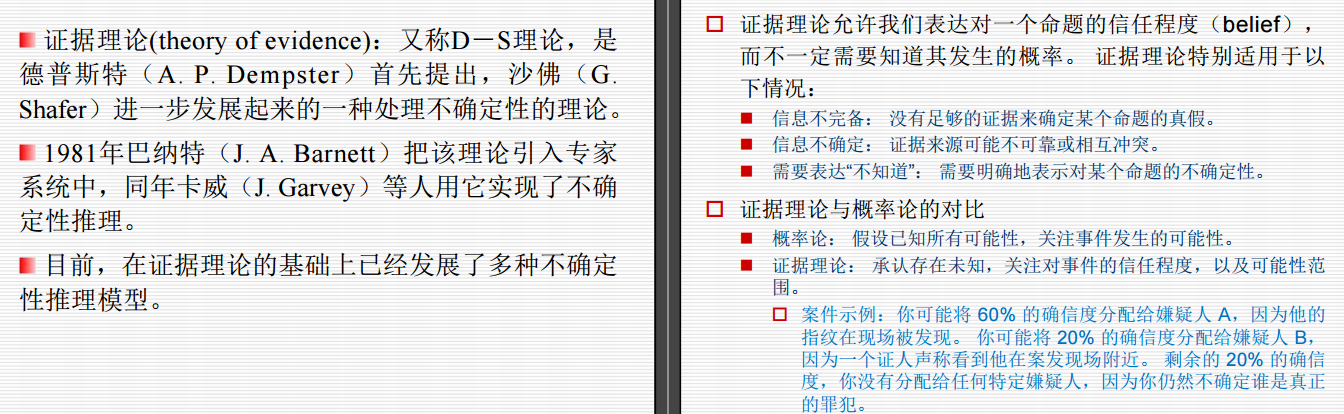
4.4 模糊推理方法

4.4.1 模糊逻辑的提出与发展

4.4.2 模糊集合

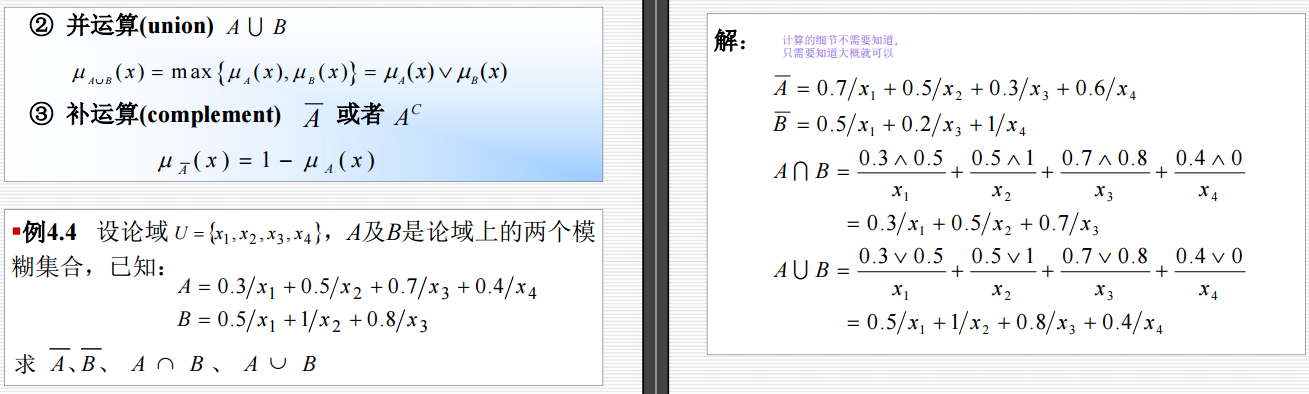
4.4.3 模糊集合的运算

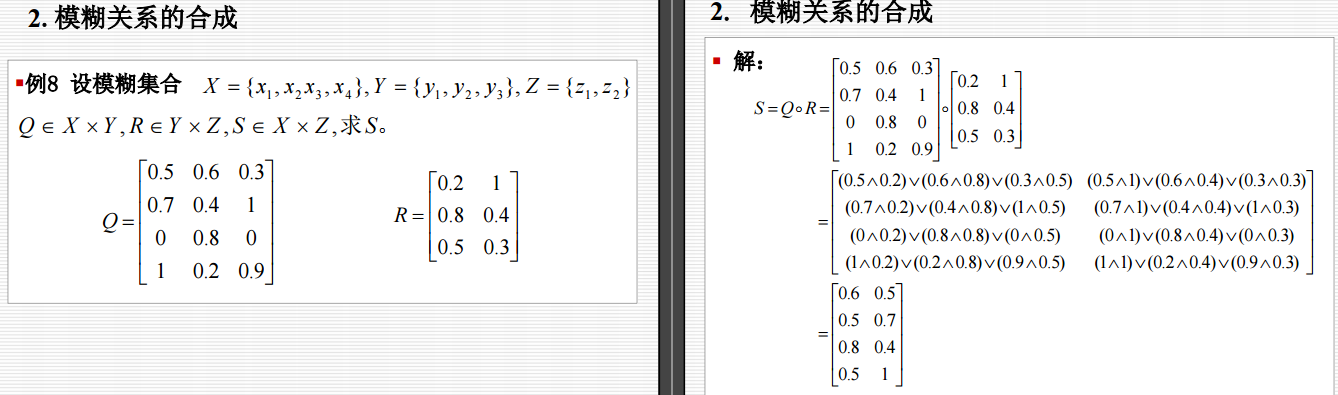
4.4.4 模糊关系与模糊关系的合成

4.4.5 模糊推理

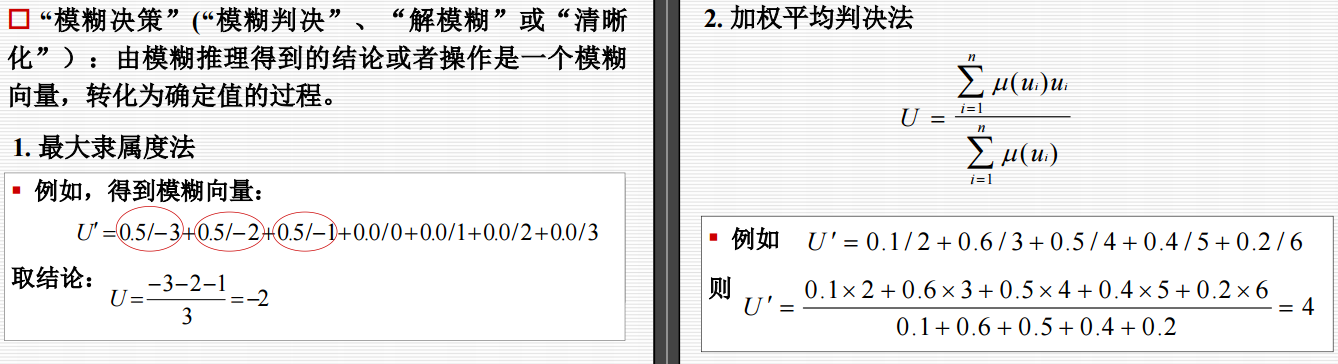
4.4.6 模糊决策

4.4.7 模糊推理的应用