当前位置：首页 > ai >正文

运筹学之引力搜索

ai 2025/7/21 22:23:16

一、历史

问：谁在什么时候提出引力搜索算法？
答：引力搜索算法（Gravitational Search Algorithm，GSA）是由伊朗学者 Esmaeil Rashedi、Hossein Nezamabadi-pour 和 Seyed S. Saryazdi 于 2009年提出的。。
论文：Rashedi, E., Nezamabadi-pour, H., & Saryazdi, S. (2009).
“GSA: A Gravitational Search Algorithm”
Information Sciences, 179(13), 2232–2248.
DOI: 10.1016/j.ins.2009.03.004
动机：群体智能优化。

二、精髓思想

精髓：万有引力！
解释：“利用解之间的引力相互作用，引导搜索群体向最优解聚集。”核心思想和传统的基于位置和速度的群体智能（如粒子群）不同，GSA 将每个个体看作有“质量”的物体，质量代表其优劣，质量越大越有吸引力，越能“拉动”其他解靠近自己。这种吸引力推动群体动态更新位置，从而寻找最优解。
通俗：就这么说吧，万有引力连解空间都适用！
伟哉，这个让牛吃草停顿了一下的男人。

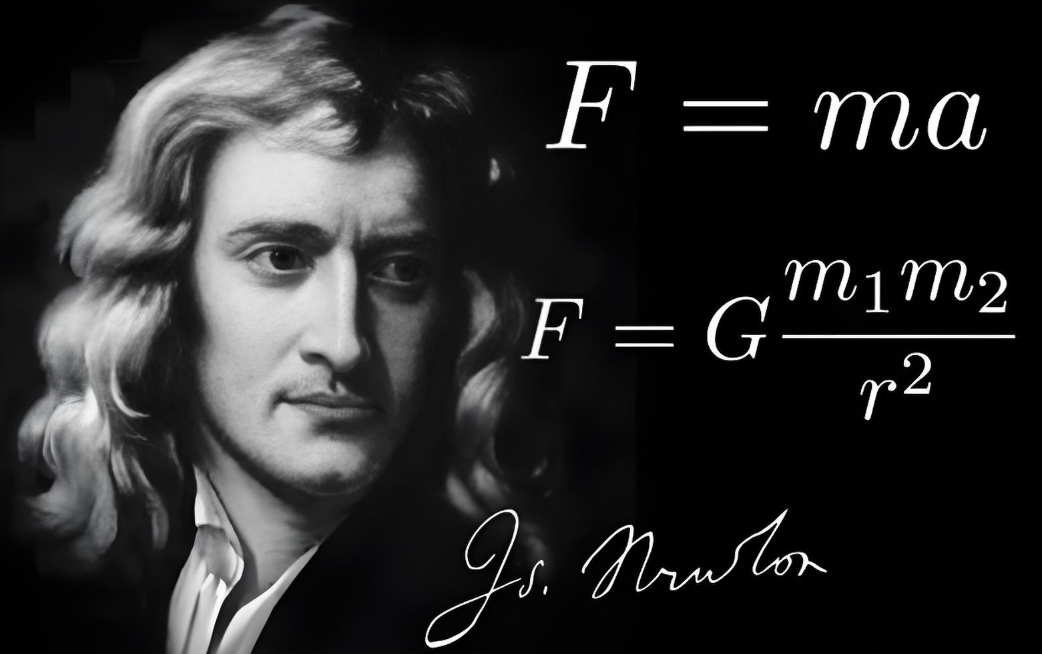
总结下来其实就5个step：

初始化一个宇宙，里面有一堆小星球（解空间→解）
计算星球（解）的质量Mass
计算两个星球（解）之间的距离R
套用万有引力公式
动起来，更新位置

三、案例与代码实现

题干：
6艘船靠3个港口，已知达到时间arrival和卸货时长handling，求最优停靠方案，即等待时长最短。
数据：

ships = {'S1': {'arrival': 0.1, 'handling': 4},'S2': {'arrival': 2.1, 'handling': 3},'S3': {'arrival': 4.2, 'handling': 2},'S4': {'arrival': 6.3, 'handling': 3},'S5': {'arrival': 5.5, 'handling': 2},'S6': {'arrival': 3.9, 'handling': 4},'S7': {'arrival': 3.7, 'handling': 4},'S8': {'arrival': 3.4, 'handling': 4},
}

实现：
step1：初始化一个宇宙，里面有一堆小星球（解空间→解）

# 初始化星球（每个个体是一个泊位分配方案）
ship_ids = list(ships.keys())   # 船名
num_ships = len(ship_ids)   # 船数
num_berths = 3  # 泊位数
population_size = 20    # 粒子数def initialize_population():return [np.random.randint(0, num_berths, size=num_ships) for _ in range(population_size)]

step2：计算星球（解）的质量Mass

质量的大小对应到就是自适应函数的值，自适应度函数如下：

# 计算适应度（总等待时间）
def calculate_fitness(assignment):berths = {i: [] for i in range(num_berths)}for i, berth in enumerate(assignment):berths[berth].append((ship_ids[i], ships[ship_ids[i]]['arrival'], ships[ship_ids[i]]['handling']))total_wait_time = 0for b in berths.values():b.sort(key=lambda x: x[1])  # 到达时间排序current_time = 0for ship_id, arrival, handling in b:start_time = max(arrival, current_time)wait_time = start_time - arrivaltotal_wait_time += wait_timecurrent_time = start_time + handlingreturn total_wait_time

那么质量如何定义呢？

# 计算每个解的得分
fitness = np.array([calculate_fitness(ind) for ind in population])
# 取最好和最差，上下限
best_idx = np.argmin(fitness)
best_solution = population[best_idx]
best_fitness = fitness[best_idx]worst = np.max(fitness)
best = np.min(fitness)# 离最差的值越远，mass就越大，同时值域放缩到0-1。1e-9意图是分母不为0。
masses = (worst - fitness) / (worst - best + 1e-9)# 使得加起来等于1，例如：
# masses = [2.1, 0.5, 1.4, 0.8]
# np.sum(masses) = 2.1 + 0.5 + 1.4 + 0.8 = 4.8
# masses = [2.1/4.8, 0.5/4.8, 1.4/4.8, 0.8/4.8] ≈ [0.4375, 0.1042, 0.2917, 0.1667]
masses = masses / np.sum(masses)

step3：计算两个星球（解）之间的距离R

如何计算两个星球的距离R（即两个泊位分配方案之间的差异程度）

# 如何计算两个粒子的距离R（即两个泊位分配方案之间的差异程度）
# 举例说明：
# 假设有4艘船：
# population[0] = [0, 1, 1, 2]  表示 S1->泊位0，S2->泊位1，S3->泊位1，S4->泊位2
# population[1] = [1, 1, 0, 2]  表示 S1->泊位1，S2->泊位1，S3->泊位0，S4->泊位2
# 差异向量为 population[0] - population[1] = [-1, 0, 1, 0]
# 欧几里得距离 R = √((-1)^2 + 0^2 + 1^2 + 0^2) = √2 ≈ 1.414
# R 表示两个方案在搜索空间中的距离，距离越小表示越相似，引力越强
R = np.linalg.norm(population[i] - population[j]) # 两个粒子的距离

step4：套用万有引力公式

有了质量，有了距离，再来个G常数，就可以直接套用万有引力公式了~

G0 = 100 # 初始引力常数
alpha = 20  # 控制G衰减的速度
max_generations = 50    # 迭代次数G = G0 * np.exp(-alpha * gen / max_generations) # 引力慢慢变小，gen 是指某次迭代gravity = compute_gravity(masses, i, j, R, G) # 引力公式# 引力函数
def compute_gravity(masses, i, j, R, G):return G * (masses[i] * masses[j]) / (R + 1e-9)

有了力还需要有方向，再加点随机因素，得到最后的合力！如下：

direction = population[j] - population[i] # 向量方向
force += random.random() * gravity * direction  # 随机扰动后的合力

step5：动起来，更新位置

有了力和方向，那就动起来吧，怎么动？那不就是物理题嘛~

acc = force / (masses[i] + 1e-9)    # 加速度a，F=m*a
velocities[i] = random.random() * velocities[i] + acc   # 速度更新 vt = v0 + at
new_pos = population[i] + velocities[i] # 更新位置

附上完整代码：

import random
import numpy as np# 船舶数据
ships = {'S1': {'arrival': 0.1, 'handling': 4},'S2': {'arrival': 2.1, 'handling': 3},'S3': {'arrival': 4.2, 'handling': 2},'S4': {'arrival': 6.3, 'handling': 3},'S5': {'arrival': 5.5, 'handling': 2},'S6': {'arrival': 3.9, 'handling': 4},'S7': {'arrival': 3.7, 'handling': 4},'S8': {'arrival': 3.4, 'handling': 4},
}ship_ids = list(ships.keys())   # 船名
num_ships = len(ship_ids)   # 船数
num_berths = 3  # 泊位数
population_size = 20    # 粒子数
max_generations = 50    # 迭代次数
G0 = 100 # 初始引力常数
alpha = 20  # 控制G衰减的速度# 初始化种群（每个个体是一个泊位分配方案）
def initialize_population():return [np.random.randint(0, num_berths, size=num_ships) for _ in range(population_size)]# 计算适应度（总等待时间）
def calculate_fitness(assignment):berths = {i: [] for i in range(num_berths)}for i, berth in enumerate(assignment):berths[berth].append((ship_ids[i], ships[ship_ids[i]]['arrival'], ships[ship_ids[i]]['handling']))total_wait_time = 0for b in berths.values():b.sort(key=lambda x: x[1])  # 到达时间排序current_time = 0for ship_id, arrival, handling in b:start_time = max(arrival, current_time)wait_time = start_time - arrivaltotal_wait_time += wait_timecurrent_time = start_time + handlingreturn total_wait_time# 引力函数
def compute_gravity(masses, i, j, R, G):return G * (masses[i] * masses[j]) / (R + 1e-9)# 主函数：引力搜索算法
def gsa_schedule():population = initialize_population()    # 初始化20个个体velocities = [np.zeros(num_ships) for _ in range(population_size)]  # 每个个体在解空间中的“速度”，初始化为 0for gen in range(max_generations):# 计算每个解的得分fitness = np.array([calculate_fitness(ind) for ind in population])# 取最好和最差，上下限best_idx = np.argmin(fitness)best_solution = population[best_idx]best_fitness = fitness[best_idx]worst = np.max(fitness)best = np.min(fitness)# 离最差的值越远，mass就越大，同时值域放缩到0-1。1e-9意图是分母不为0。masses = (worst - fitness) / (worst - best + 1e-9)# 使得加起来等于1，例如：# masses = [2.1, 0.5, 1.4, 0.8]# np.sum(masses) = 2.1 + 0.5 + 1.4 + 0.8 = 4.8# masses = [2.1/4.8, 0.5/4.8, 1.4/4.8, 0.8/4.8] ≈ [0.4375, 0.1042, 0.2917, 0.1667]masses = masses / np.sum(masses)G = G0 * np.exp(-alpha * gen / max_generations) # 引力慢慢变小# 两两粒子计算for i in range(population_size):force = np.zeros(num_ships)for j in range(population_size):if i != j:# 如何计算两个粒子的距离R（即两个泊位分配方案之间的差异程度）# 举例说明：#   假设有4艘船：#     population[0] = [0, 1, 1, 2]  表示 S1->泊位0，S2->泊位1，S3->泊位1，S4->泊位2#     population[1] = [1, 1, 0, 2]  表示 S1->泊位1，S2->泊位1，S3->泊位0，S4->泊位2#   差异向量为 population[0] - population[1] = [-1, 0, 1, 0]#   欧几里得距离 R = √((-1)^2 + 0^2 + 1^2 + 0^2) = √2 ≈ 1.414#   R 表示两个方案在搜索空间中的距离，距离越小表示越相似，引力越强R = np.linalg.norm(population[i] - population[j]) # 两个粒子的距离gravity = compute_gravity(masses, i, j, R, G) # 引力公式direction = population[j] - population[i] # 向量方向force += random.random() * gravity * direction  # 随机扰动后的合力acc = force / (masses[i] + 1e-9)    # 加速度a，F=m*avelocities[i] = random.random() * velocities[i] + acc   # 速度更新 vt = v0 + atnew_pos = population[i] + velocities[i] # 更新位置# 保证位置合法new_pos = np.clip(np.round(new_pos), 0, num_berths - 1)population[i] = new_pos.astype(int)return best_solution, best_fitnessif __name__ == "__main__":# 执行算法best_assignment, best_total_wait = gsa_schedule()# 输出调度结果berth_assignments = {i: [] for i in range(num_berths)}for idx, berth in enumerate(best_assignment):ship = ship_ids[idx]berth_assignments[berth].append((ship, ships[ship]['arrival'], ships[ship]['handling']))# 展示调度排序（按到达时间排序）for berth, ship_list in berth_assignments.items():ship_list.sort(key=lambda x: x[1])print(f"\n泊位 {berth + 1}：")for ship_id, arrival, handling in ship_list:print(f"  {ship_id}: 到达 {arrival}, 作业 {handling}")print(f"\n🚢 最小总等待时间：{best_total_wait:.2f}")