用整数划分整理结构

在行列可自由变换的平面上4点结构有16个

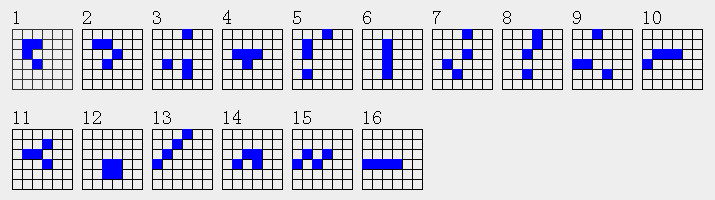
4的整数划分有5种，

4
1111	5	9,10,13,15,16,
112	5	2,4,7,11,14,
22	3	1,8,12,
13	2	3,5,
4	1	6

列分布为1111的结构有4个，9,10,13,15,16,

用同样的方法统计2，3，4，5，6点结构得到

2	3		3	6		4	16		5	34		6	90
11	2		111	3		1111	5		11111	7		111111	11
1	1		12	2		112	5		1112	9		11112	17
			3	1		22	3		122	7		1122	19
						13	2		23	3		222	8
						4	1		113	5		1113	10
									14	2		123	10
									5	1		33	4
												114	5
												24	3
												15	2
												6	1

很直观

2			3			4			5			6
11	2		111	3		1111	5		11111	7		111111	11	p(a)
1	1		3	1		4	1		5	1		6	1	n

显然每组的第一行就是整数划分，如p（6）=11，则当a=6时，111111分布共可容纳11个不同的结构。

而最后一行就是a个点排成一列，就是一个。

3			4			5			6
12	2		13	2		14	2		15	2	1n

在第a=3，4，5，6组中都有一种分布1n,可容纳结构的数量都是2个。

当a=3时

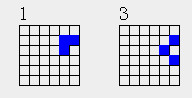
只有两种可能，1与2同行，1与 2不同行。

当a=4，5时

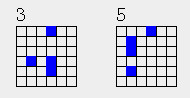
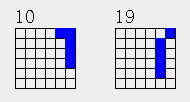
明显，这种1n类分布，只要n>=1,都只能有2个

4			5			6
22	3		23	3		24	3	2n

在4，5，6中都有2n类分布，数量都是3个

当a=4时

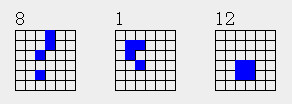
只有0，1，2行相交3种情况

当a=5时同样。所以对于这种2n类分布，只要n>=2都有3个结构。

4			5			6
112	5		113	5		114	5	11n

在4，5，6中都有11n类分布，数量都是5个

11n类分布有3层，其中11是已知有2个

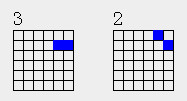
一种有2个

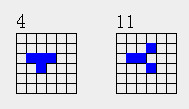
第2种有3个

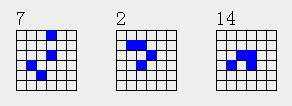
因此只要这种11n类分布，n>=2都有5个。

5				6
122	7	12n	x	123	10	12n

在5中有122，在6中有123，他们都是12n类分布，12值已知有2个

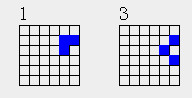
同样可以按照相交点的数量计算结构的总数

1	1		0	1		3
	1				2	3

一个结构只有4种相交方式

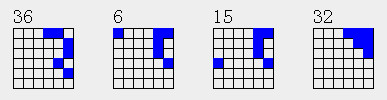
1			0	1			4	5
	1					3	4	5
	1				2	3		5

1个有6种相交方式

所以12n类分布，当n>=3的时候都有10个。

122分布，

1	1		0	1		3
	1				2	3

一种结构仍然有4个

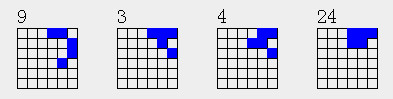
1			0	1			4
	1					3	4
	1				2	3

一个结构可以有5个

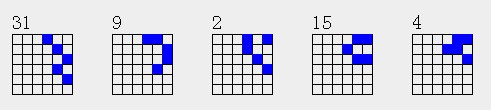
但9重复了一次，4重复了1次，因此122只有7个，是不饱和的。

5				6
1112	9	111n	x	1113	10	111n

在5和6中都有111n类分布，分布111已知有3个

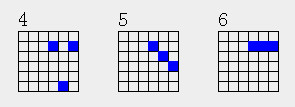
先考虑1113分布

1	1	1		0
					1

一种情况有2个

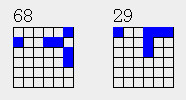
1	1			0	1		3
		1				2	3

一种情况有4个

 

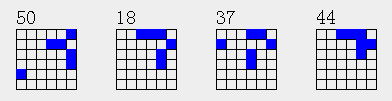
		1		0	1	2	3
	1					2	3
1							3

第3种情况也有4个

 

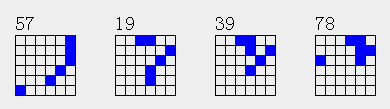
所以111n只要n>=3都有10个

当分布为1112时

第3组为

		1		0	1	2
	1					2
1

前2组不变，且没有简并的情况，因此1112只有9个，是不饱和的。

因此得到表格

2			3			4			5				6
11	2	1n	111	3		1111	5		11111	7			111111	11
													11112	17	x
													1122	19	x
													222	8	x
									1112	9	111n	x	1113	10	111n
									122	7	12n	x	123	10	12n
													33	4
						112	5	11n	113	5	11n		114	5	11n
						22	3	2n	23	3	2n		24	3	2n
			12	2	1n	13	2	1n	14	2	1n		15	2	1n
1	1	n	3	1	n	4	1	n	5	1	n		6	1	n

2，3，4，5的数量都可以被解释，其中2，3，4都是由饱和分布构成，而5由5个饱和分布和2个不饱和分布构成。