机器学习周报-文献阅读

摘要

本周阅读了一篇基于深度分解结构和自相关的大规模水质预测的论文，文章介绍了一种大规模水质预测模型–SVD-Autoformer。该算法结合了Savitzky-Golay（SG）滤波器、变分模式分解（VMD）、自相关机制和深度分解结构，并在Transformer改造中实现。第一，SG滤波器去除噪声，同时保留有价值的数据特征。SVDAutoformer采用SG滤波器作为数据预处理工具，以减少噪声并防止非线性模型过拟合。其次，VMD提取了信号的主要模态及其中心频率，从而为预测提供了更丰富的特征。第三，具有嵌入式分解模块的深度分解架构允许在预测过程期间进行渐进分解。SVD-Autoformer利用该架构从复杂的水质时间序列中提取出更具可预测性的成分，用于长期预测。最后，利用自相关机制捕捉时间相关性，提高信息利用率。

Abstract

This week, I read a paper on large-scale water quality prediction based on deep decomposition structures and autocorrelation. The paper introduces a large-scale water quality prediction model called SVD-Autoformer. This algorithm integrates the Savitzky-Golay (SG) filter, Variational Mode Decomposition (VMD), autocorrelation mechanisms, and deep decomposition structures, implemented within a Transformer framework. First, the SG filter removes noise while preserving valuable data features. SVD-Autoformer employs the SG filter as a data preprocessing tool to reduce noise and prevent overfitting in nonlinear models. Second, VMD extracts the main modes of the signal and their central frequencies, providing richer features for prediction. Third, a deep decomposition architecture with an embedded decomposition module enables progressive decomposition during the prediction process. SVD-Autoformer leverages this architecture to extract more predictable components from complex water quality time series for long-term forecasting. Finally, the autocorrelation mechanism is used to capture temporal dependencies, improving information utilization.

1 文章内容

1.1 相关工作

1.1.1 时间序列预测模型

该研究中的SG滤波器在消除噪声的同时有效地保留了基本的时间序列特征。外部分解模块的VMD提高了时间序列中信息的利用率。深度分解架构的内部序列分解模块利用数据的抽象特征。这些优点的结合使得模型能有效提高预测精度。;

1.1.2 时间序列的降噪

该研究利用SG滤波器作为数据预处理工具来降低噪声。它可以成功地消除噪声分量，同时保留数据的特征。另一方面，SG滤波器提供了一种计算复杂度低的线性方法，特别是在处理大规模时间序列数据时。相比之下，小波变换和经验模式分解（EMD）涉及多级分解和重构过程，具有更高的计算复杂度。

1.1.3 时间序列的分解

该研究创新性地设计了外部和内部分解模块。
在外部分解模块中采用了自适应信号分解方法VMD。它捕捉时间序列中的局部变化，并为后续的预测建模提供更丰富的特征。
在内部分解模块中，我们引入了深度分解架构，它可以更好地捕获时间序列中更可预测的成分。 提出的模型中，外部分解模块的VMD更好地捕捉了时间序列中的局部变化。内部分解模块的深度分解体系结构进一步利用数据的抽象特征来更好地表示全局特征。这两个分解模块相互补充，从而增强了模型的预测性能。

1.2 模型框架

水质预测涉及使用水质指标传感器收集数据，然后分析历史时间序列数据以预测这些指标的未来趋势。利用水质指标，如pH值，电导率（EC），总氮（TN）和溶解氧（DO）。传感器定期对这些指标进行采样，以监测水质。设$Y=y_1，y_2，...，y_l$表示来自过去l个时间点的水质时间序列,SG滤波器应用于Y，产生$\bar{Y}={\bar{y}}_1，{\bar{y}}_2，...，{\bar{y}}_l$表示过去l个时间点的噪声降低后的水质指标。该研究预测了接下来n个时间点的数据，表示为${\hat{H}}_n={\hat{h}}_{l+1}，{\hat{h}}_{l+2}，...，{\hat{h}}_{l+n}$。此外，${\hat{H}}_n={\hat{h}}_{l+1}，h_{l+2}，...，h_{l+n}$}表示真实的未来水质指标。

1.2.1 SG Filter

噪声的存在会导致非线性方法过拟合。使用SG滤波器对原始数据进行平滑处理，从而降低噪声并防止非线性模型过度拟合。SG滤波器应用线性最小二乘法将低阶多项式拟合到相邻数据点的连续子集，如下所示

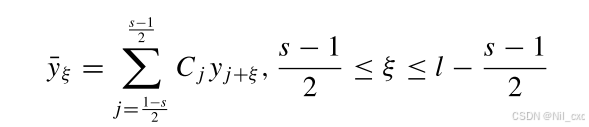
其中，${\hat{y}}_{\zeta }$表示经过SG滤波器处理后的水质指标数据，${\hat{y}}_{j+\zeta }$表示窗口中的水质指标，s和l表示SG过滤器的尺寸和水指示器的长度。采用s卷积系数最小二乘法拟合水质时间序列指标${\hat{y}}_{j+\zeta }$

1.2.2 变分模式分解(VMD)

时间序列数据通常包含不同尺度和频率的各种成分，例如趋势，季节，周期项和噪声。这些组成部分相互作用，使时间序列预测变得复杂和困难。基于时频的分解可以将时间序列数据分解为一组固有模态函数（IMF）和残差，从而更好地表示不同尺度的分量。常用的分解方法是EMD，它将时间序列分解为不同频率范围的IMF。每个IMF代表一个局部振动模式，因此，EMD可以适应非光滑和非线性时间序列。然而，EMD有可能在包含大量噪声的时间序列中产生模态混叠，从而影响最终分解数据的可用性。

为了克服EMD的局限性，这项工作引入VMD方法作为一个更有利的分解技术。VMD可以提取信号的中心模式函数及其各自的中心频率。它是一种非递归的信号分解技术，每个模式主要集中在中心频率周围。在变分框架中，信号分解的问题被转化为约束变分模型的最优解，如下所示

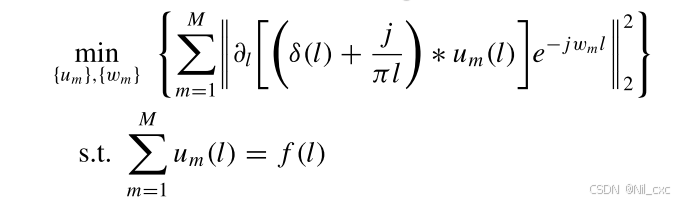
1.2.3 SVD-Autoformer Model

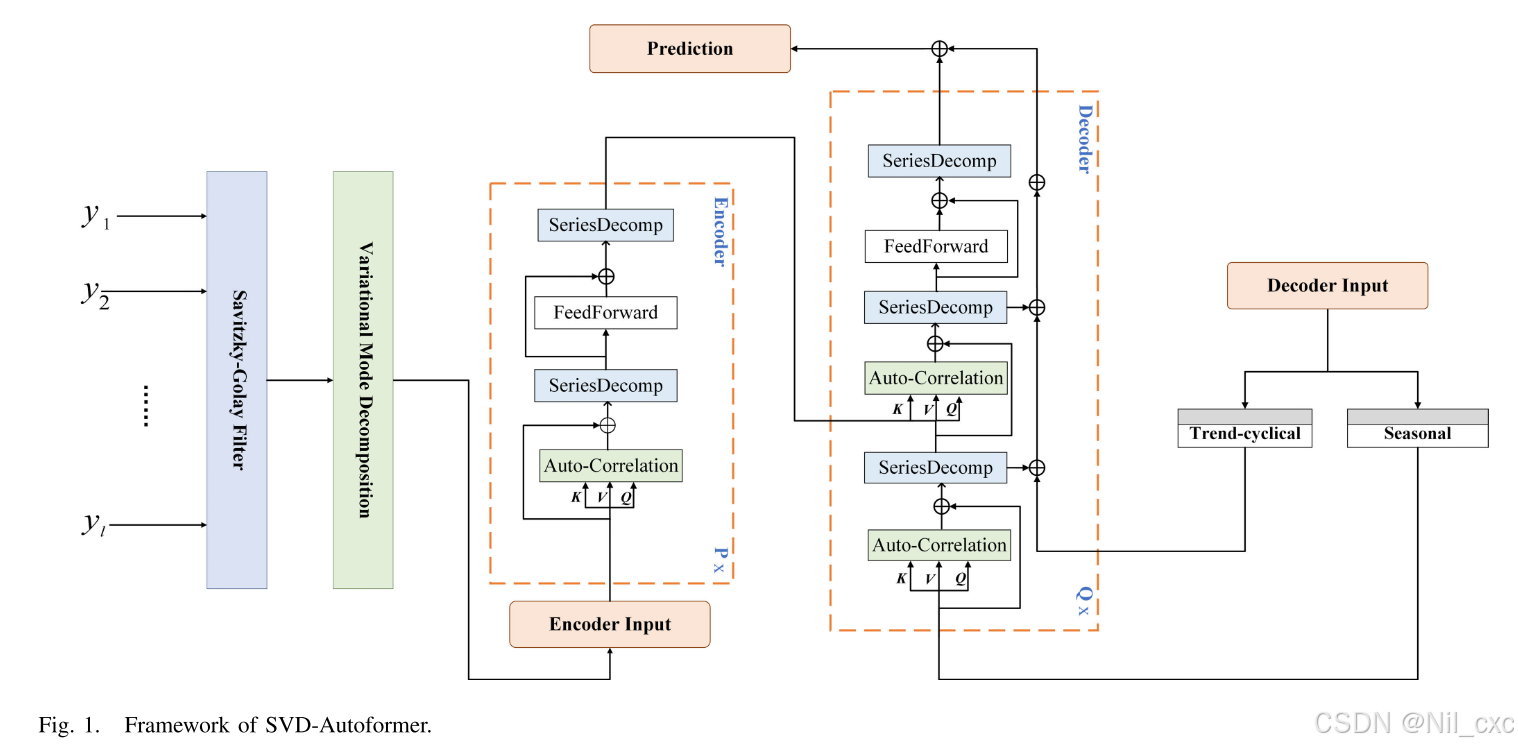
如图所示，深度分解架构包括内部分解模块、自相关机制以及相关联的编码器和解码器组件。深度分解架构基于Transformer 。编码器-解码器架构在结构内具有显著变化。首先，将添加的分解模块嵌入内部。此外，自相关机制被用来代替Transformer的自我注意机制。
首先，SG过滤器执行对水质时间序列进行去噪处理。VMD用于分解，以获得更丰富的预测特征。此外，SVD-Autoform的编码器还包含自相关机制和分解模块。它通过内部序列分解模块对趋势周期分量进行分解，并对残差进行分析。最后，季节分量被送入解码器，并与编码器中的趋势周期分量累积，以创建未来预测。此外，SVD-Autoform的伪代码和总体流程图分别如算法1和图2所示。

1.内部序列分解

时间序列数据可以被认为是几个组成部分的组合，表示如下：$Y_l=C_l+T_l+R_l$，其中，$Y_l$表示水质指标的时间序列数据，$C_l$表示趋势-周期分量，$T_l$表示季节分量，$R_l$表示残差分量。

一般来说，预测方法使用分解作为时间序列数据的预处理步骤，但这种操作错过了未来时间序列中组件之间的相互作用。相比之下，SVD-Autoformer使用分解作为嵌入式操作模块，从复杂的水质时间序列中提取更有价值的特征。首先，SVDAutoformer应用移动平均线来平滑周期性波动，突出长期趋势。然后，应用填充操作以保持序列长度的一致性。这里， Y = { y 1 ， y 2 ， . . . ， y l } Y = \{y_1，y_2，...，y_l \} Y={y1​，y2​，...，yl​}表示长度为l的水质指标时间序列。分解过程描述如下：

$Y_c=AvgPool(Padding(Y))$

$Y_t=Y-Y_c$

其中$Y_c$表示趋势周期分量，使用AvgPool（·）导出，并进行填充以保留时间序列长度。$Y_t$表示季节分量，由Y去除$Y_c$得出。

2.Encoder

编码层由两个内部序列分解模块组成。首先，编码器输入长度为L的时间序列Y，两个模块使用AvgPool(·)去除趋势周期分量。然后，编码器分离出剩余的分量，去除趋势周期分量，并专注于对季节分量进行建模。编码器的输出分量由季节分量组成，其用于在解码器中细化预测结果。第1个编码器可以表示为$Y_{en}^j=Encoder（Y_{en}^{j-1}）$。编码器的过程如下所示：

$T_{en}^{j,1}=Decomp(Auto-Correlation(Y_{en}^{j-1})+Y_{en}^{j-1})$
$T_{de}^{j,2}=Decomp(FeedForawrd(T_{en}^{j,1})+T_{en}^{j,1})$

其中$T_{en}^{j,k}$表示第j层编码器中第k级数分解模块提取的季节分量，其中j∈[1，…，P]和k∈[1，2]。$Y_{en}^j$表示第j层编码器的结果

3.Decoder

解码器的输入包括两个分量，即，趋势-周期成分和从内部序列分解获得的季节成分。解码器的左侧部分侧重于通过将剩余分量与趋势周期性分量分离来细化趋势。右侧部分累积来自编码器的细化趋势和趋势循环分量。解码器的过程如下：

$T_{de}^{j,1},C_{de}^{j,1}=Decomp(Auto-Correlation(Y_{de}^{j-1})+Y_{de}^{j-1})$
$T_{de}^{j,2},C_{de}^{j,2}=Decomp(Auto-Correlation(T_{de}^{j,1},Y_{en}^p)+T_{de}^{j,1})$

$T_{de}^{j,3},C_{de}^{j,3}=Decomp(FeedForward(T_{de}^{j,2})+T_{de}^{j,2})$

其中$T_{de}^{j,k}$和$C_{de}^{j,k}$表示第j层解码器中的第k个系列分解模块的季节性和趋势循环分量，其中j∈[1，…，Q]和k∈[1，2，3]。$Y_{de}^j$表示第j层解码器的输出。P表示编码器的数量。$Y_{en}^P$表示具有P层的编码器的输出。

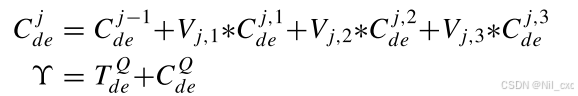
其中$V_{j,k}$表示第j层解码器中的趋势投影，其中k个系列分解模块细化趋势。表示第j层解码器中累积的趋势循环分量。Q表示解码器的数量。$T_{de}^Q$和$C_{de}^Q$表示季节性分量和趋势周期性分量，它们在由第Q层解码器处理后获得的。${\rm Y}$表示通过累积Q层解码器的趋势循环和季节分量而获得的未来预测。

4.自相关机制(Auto-correlation Mechanism)

自相关机制可以提供基于时间序列数据的周期性的序列级连接，这扩展了信息利用。首先，我们利用快速傅立叶变换来计算自相关系数，从而捕获时延相似性。自相关机制通过计算序列自相关来识别基于周期的依赖性，并最终通过时延聚合来组合相似的依赖性。随机过程理论表明，对于离散时间过程，可以获得自相关系数，其中：

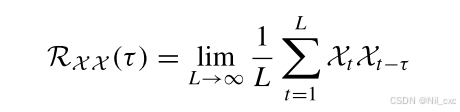
其中$R_{XX}(\tau )$表示自相关系数。$X_t$和$\tau$表示离散时间过程和时间延迟。

1.3 实验

两个真实世界的水质数据集被用来验证SVD的预测性能。京津冀和亚拉巴马数据集：数据1和数据2。京津冀数据集来自国家地表水水质自动实时监测系统。该数据集涵盖2018年8月至2022年12月。它包括每四小时采集的大约8000个样本。水质指标包括pH、EC、TN和DO。在多指标预测中，利用这四个水质指标对TN的未来值进行预测。亚拉巴马数据集记录了美国亚拉巴马的卡哈巴河的水质数据。数据集涵盖2017年5月至2019年8月。它包括每小时采集的约20，000个样本。水质指标为DO，该数据集用于在单指标预测中预测未来的DO。按照70%、10%和20%的比例，数据集被分为训练集、验证集和测试集。

1.3.1 评估指标

为了评估SVD-Autoformer和代表性方法的准确性，我们采用了三个评估指标，包括均方根误差（RMSE），平均绝对百分比误差（MAPE），平均绝对误差（MAE）。这些指标的值越低，表示预测性能越好。它们被定义为：

1. $\text{RMSE}=\sqrt{\frac{1}{L}{\sum }_{l=1}^L(y_l-{\hat{y}}_l{)}^2}$
2. $\text{MAPE}=\frac{1}{L}{\sum }_{l=1}^L\left|\frac{y_l-{\hat{y}}_l}{y_l}\right|\times 100\%$
3. $\text{MAE}=\frac{1}{L}{\sum }_{l=1}^L|y_l-{\hat{y}}_l|$

其中L表示原始数据的总数。$y_l$和${\hat{y}}_l$表示地面实况和预测值。

1.3.2 实验对比

数据预处理
首先，我们使用z分数标准化方法对数据进行标准化，该方法将数据转换为均值为0、方差为1的标准正态分布。这里，y表示原始数据，y '表示标准化数据，μ表示原始数据的平均值，σ表示原始数据的标准差。公式如下：$y^{\prime }=\frac{y-\mu }{\sigma }$。然后，我们应用SG滤波器来降低数据噪声。证明SG滤波器在增强模型预测方面优于其他滤波器方法，我们将其与典型的移动平均（MA）滤波器和移动中值（MM）滤波器。我们在数据1和数据2上进行实验以比较SG、MM和MA滤波器。表I给出了具有不同窗口大小的三个滤波器的RMSE值。SG滤波器对于各种窗口大小具有最低的RMSE值，表明模型预测改进更好。
为了优化SG滤波器的降噪能力，我们采用不同多项式阶数（k）的SG滤波器，窗口大小对数据1和数据2执行实验。表II给出了不同k和s的RMSE值。结果表明，对于数据1（数据2），当k =3和s =5（k =3和s =7）时，SVD-Autoformer具有最佳预测。

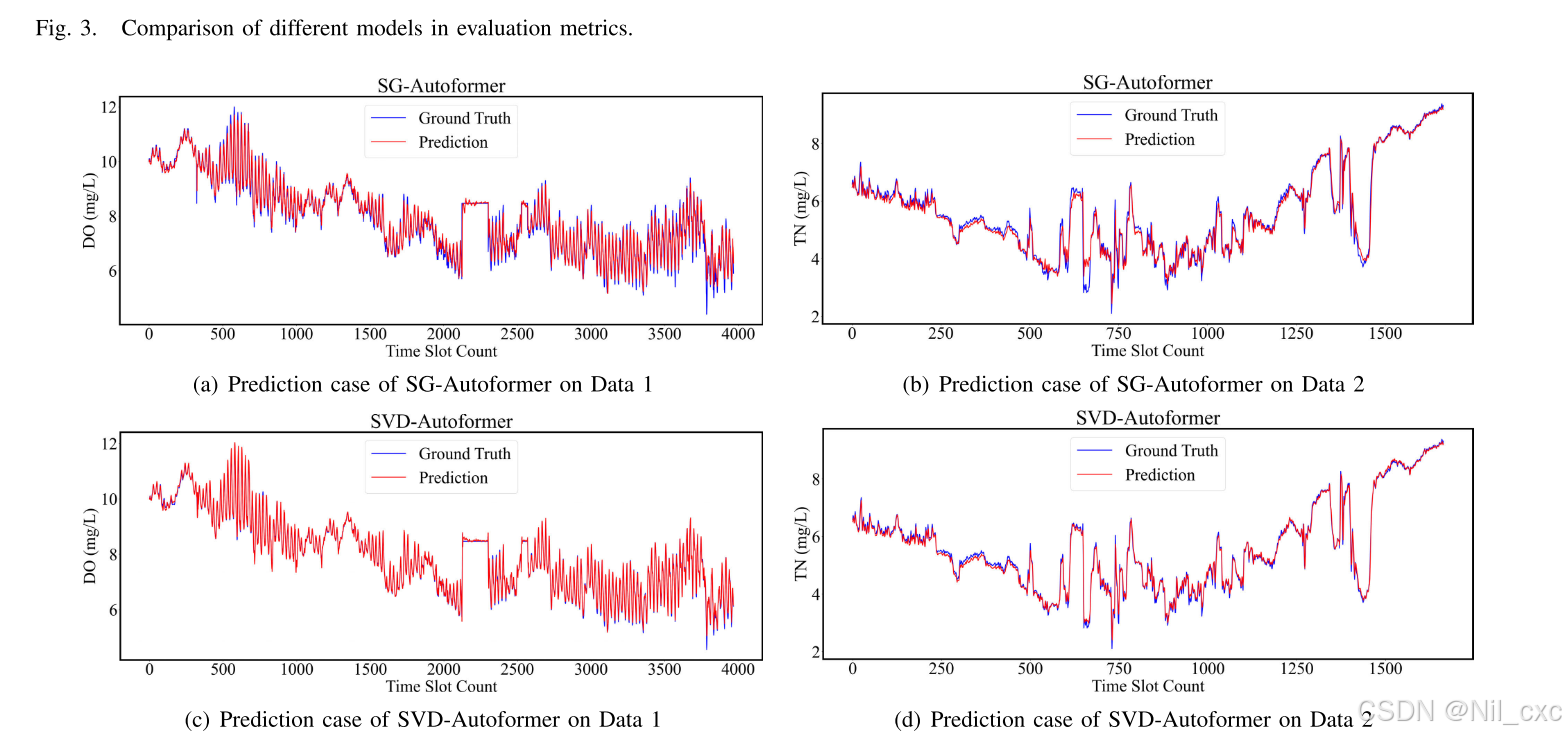
如图显示了SVD自动生成器对长期预测的评价指标。实验结果表明，SVD-Autoformer在长步长预测方面优于其他基准模型。例如，在一步预测中，RMSE、MAE和MAPE值分别下降了61%、65%和73%。它们在五步、十步和十五步预测中也有显著下降。

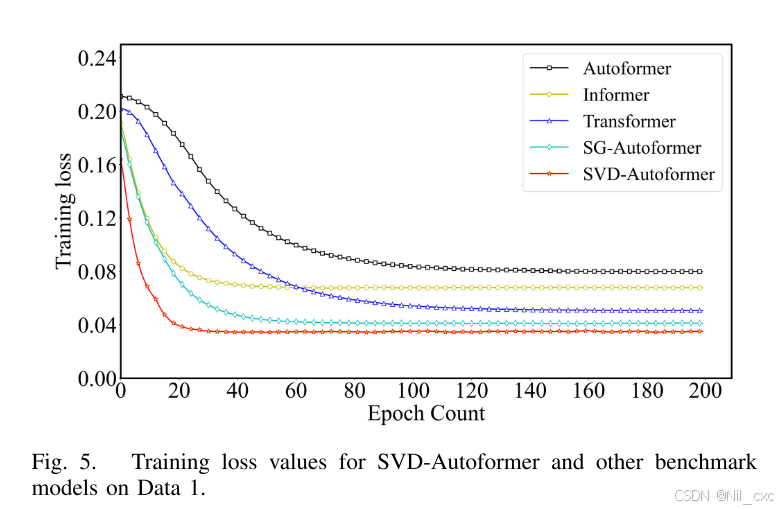
为了直观地显示SVD-Autoformer具有更好的预测性能，文章中将预测步长的长度设置为1。然后，对SG-Autoformer和SVD-Autoformer进行了对比实验。上图（a）和上图（c）示出了数据1的实际TN值和预测TN值的拟合结果。红色曲线表示预测值，而蓝色曲线表示实际值.SVD-Autoformer的TN预测值与真实值之间具有较好的拟合性能。在不同的迭代中，SVD自动生成器和基准模型的训练损失值如下图所示。SVD-Autoformer的训练损失值较低，且随着迭代次数的增加而保持稳定。

2 相关知识

2.1 变分模式分解（VMD）

变分模式分解（Variational Mode Decomposition, VMD）是一种用于信号处理的自适应信号分解方法，特别适用于处理非平稳和非线性信号。VMD通过将信号分解为多个固有模态函数（Intrinsic Mode Functions, IMFs），每个IMF具有不同的中心频率和带宽，从而能够有效地提取信号中的多尺度特征。
VMD的核心思想是通过变分优化问题来寻找信号的最佳分解方式，确保每个IMF在频域上是紧凑的，并且能够很好地表示信号的局部特征。

VMD的基本原理
VMD的目标是将一个输入信号$f(t)$分解为K个IMF，每个IMF$u_k(t)$都具有明确的中心频率$w_k$。VMD通过求解一个约束变分问题来实现这一目标，具体步骤如下：

1. 希尔伯特变换：首先对每个IMF$u_k(t)$ 进行希尔伯特变换，得到其解析信号：
   $\left(\delta (t)+\frac{j}{\pi t}\right)\ast u_k(t)$
   其中，$\delta$是单位脉冲函数，$j$是虚数单位，*表示卷积运算。
2. 频率调制：对每个IMF的解析信号进行频率调制，将其频谱移动到基带：
   $\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast u_k(t)\right]e^{-j{\omega }_{k}t}$
   其中， $w_k$是第k个IMF的中心频率。
3. 带宽约束：通过施加带宽约束，确保每个IMF在频域上是紧凑的。VMD的约束变分问题可以表示为：
   min ⁡ { u k } , { ω k } { ∑ k ∥ ∂ t [ ( δ ( t ) + j π t ) ∗ u k ( t ) ] e − j ω k t ∥ 2 2 } \min_{\{u_k\},\{\omega_k\}} \left\{ \sum_k \left\| \partial_t \left[ \left(\delta(t) + \frac{j}{\pi t}\right) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 \right\} min{uk​},{ωk​}​{∑k​ ​∂t​[(δ(t)+πtj​)∗uk​(t)]e−jωk​t ​22​}
   约束条件为：${\sum }_k{u}_k=f(t)$
   其中， ${\partial }_t$表示时间导数， $|{|}_2^2$表示$L_2$范数
4. 增广拉格朗日函数：为了求解上述约束变分问题，引入增广拉格朗日函数 L：
   L ( { u k } , { ω k } , λ ) = α ∑ k ∥ ∂ t [ ( δ ( t ) + j π t ) ∗ u k ( t ) ] e − j ω k t ∥ 2 2 + ∥ f ( t ) − ∑ k u k ( t ) ∥ 2 2 + ⟨ λ ( t ) , f ( t ) − ∑ k u k ( t ) ⟩ \begin{aligned} \mathcal{L}(\{u_k\},\{\omega_k\},\lambda) &= \alpha \sum_k \left\|\partial_t \left[ (\delta(t)+\frac{j}{\pi t})*u_k(t) \right] e^{-j\omega_k t}\right\|_2^2 \\ &\quad + \left\| f(t) - \sum_k u_k(t) \right\|_2^2 \\ &\quad + \langle \lambda(t), f(t) - \sum_k u_k(t) \rangle \end{aligned} L({uk​},{ωk​},λ)​=αk∑​ ​∂t​[(δ(t)+πtj​)∗uk​(t)]e−jωk​t ​22​+ ​f(t)−k∑​uk​(t) ​22​+⟨λ(t),f(t)−k∑​uk​(t)⟩​
   其中，$\alpha$是惩罚因子，$\lambda (t)$是拉格朗日乘子。

VMD的优点

1. 自适应性强：VMD不需要预先设定基函数，能够根据信号的特征自适应地分解出多个IMF，每个IMF都具有明确的物理意义。
2. 抗噪能力强：VMD通过带宽约束和频率调制，能够有效抑制噪声，提取信号中的有用信息。
3. 避免模态混叠：与经验模态分解（EMD）相比，VMD能够有效避免模态混叠问题，确保每个IMF在频域上是紧凑的。

变分模式分解（VMD）是一种强大的信号分解方法，能够有效处理非平稳和非线性信号。通过将信号分解为多个IMF，VMD能够提取信号中的多尺度特征，降低信号的复杂性和非平稳性。在风电功率预测中，VMD能够显著提高预测模型的精度和稳定性。尽管VMD存在参数选择和计算复杂度较高的局限性，但其在信号处理领域的应用前景广阔，特别是在处理复杂信号和噪声抑制方面表现出色。

相关代码

import torch
import torch.fft
import numpy as np
import matplotlib
matplotlib.use('TkAgg')  # 切换到 TkAgg 后端
import matplotlib.pyplot as pltdef vmd(signal, num_modes=3, alpha=2000, tau=0, max_iter=500, tol=1e-7):"""Variational Mode Decomposition (VMD) using PyTorch.参数:signal (torch.Tensor): 输入信号 (1D tensor)num_modes (int): 分解的模态数量 Kalpha (float): 带宽惩罚参数tau (float): 时间步长参数 (通常设为 0)max_iter (int): 最大迭代次数tol (float): 收敛容差返回:u (torch.Tensor): 分解得到的模态分量 (num_modes x signal_length)omega (torch.Tensor): 每个模态的中心频率"""# 确保输入信号是 PyTorch 张量if not torch.is_tensor(signal):signal = torch.tensor(signal, dtype=torch.float32)signal = signal.to(torch.float32)N = signal.shape[0]  # 信号长度# 初始化模态分量和中心频率u = torch.zeros((num_modes, N), dtype=torch.float32)  # 模态分量omega = torch.linspace(0, 0.5, num_modes, dtype=torch.float32)  # 初始中心频率lambda_ = torch.zeros(N, dtype=torch.float32)  # 拉格朗日乘子# 计算单边频谱f = torch.fft.rfft(signal)freqs = torch.fft.rfftfreq(N)# 迭代优化for _ in range(max_iter):u_old = u.clone()for k in range(num_modes):# 更新每个模态分量# 计算残差residual = signal - torch.sum(u, dim=0) + u[k]# 傅里叶变换u_hat = torch.fft.rfft(residual)lambda_hat = torch.fft.rfft(lambda_)  # 对 lambda_ 进行傅里叶变换# 频域更新公式denominator = 1 + 2 * alpha * (freqs - omega[k]) ** 2u_hat_k = (u_hat - lambda_hat / 2) / denominator# 逆傅里叶变换回到时域u[k] = torch.fft.irfft(u_hat_k, n=N)# 更新中心频率for k in range(num_modes):u_hat_k = torch.fft.rfft(u[k])power_spectrum = torch.abs(u_hat_k) ** 2omega[k] = torch.sum(freqs * power_spectrum) / torch.sum(power_spectrum)# 更新拉格朗日乘子（时域）lambda_ = lambda_ + tau * (torch.sum(u, dim=0) - signal)# 检查收敛if torch.norm(u - u_old) / torch.norm(u_old) < tol:breakreturn u, omega# 示例使用
# 示例使用
if __name__ == "__main__":# 生成一个测试信号t = torch.linspace(0, 1, 1000)signal = (torch.sin(2 * np.pi * 5 * t) +0.5 * torch.sin(2 * np.pi * 15 * t) +0.2 * torch.randn(1000))# 运行 VMDnum_modes = 2u, omega = vmd(signal, num_modes=num_modes, alpha=2000, tau=0)# 打印结果print("模态分量形状:", u.shape)print("中心频率:", omega)# 可视化plt.figure(figsize=(10, 6))plt.subplot(num_modes + 1, 1, 1)plt.plot(signal.numpy(), label="Original Signal")plt.legend()for k in range(num_modes):plt.subplot(num_modes + 1, 1, k + 2)plt.plot(u[k].numpy(), label=f"Mode {k + 1}")plt.legend()plt.tight_layout()plt.show()

其中，对于模态分量形状，2表示指定的模态数量，1000为输入信号的长度。中心频率是每个模态分量在频域中的主要振荡频率。VMD 通过优化算法调整这些频率，使每个模态的带宽最小化，同时保持分解的有效性。

原始信号（第一张子图）：显示输入信号的波形，例如一个包含 5 Hz 和 15 Hz 正弦波以及噪声的混合信号。
分解后的模态分量（后续子图），每个模态单独绘制，展示它们各自的波形。

2.2 SVD-Autoformer代码

SVD-Autoformer伪代码

import torch
import torch.nn as nn
import mathclass SVDAutoformer(nn.Module):def __init__(self, input_length, num_encoder_layers, num_decoder_layers, d_model=512):super(SVDAutoformer, self).__init__()self.input_length = input_lengthself.d_model = d_modelself.num_encoder_layers = num_encoder_layersself.num_decoder_layers = num_decoder_layers# Embedding layersself.encoder_embedding = nn.Linear(1, d_model)self.decoder_embedding = nn.Linear(1, d_model)# Encoder and Decoder layersself.encoder_layers = nn.ModuleList([AutoCorrelationLayer(d_model) for _ in range(num_encoder_layers)])self.decoder_layers = nn.ModuleList([DecoderLayer(d_model) for _ in range(num_decoder_layers)])# Final output layerself.output_layer = nn.Linear(d_model, 1)def decompose(self, x):U, S, V = torch.svd(x)return U, S, Vdef forward(self, Y):# Step 1: Decompose input seriesY_ens, Y_ent = self.decompose(Y[:, :self.input_length//2])# Step 2: Concatenate with placeholdersY0 = torch.zeros_like(Y_ent)Y_mean = torch.mean(Y_ent, dim=1, keepdim=True)Y_des = torch.cat([Y_ent, Y0], dim=1)Y_det = torch.cat([Y_ent, Y_mean], dim=1)# Step 3: Embed encoder inputY_en = self.encoder_embedding(Y[:, :, None])# Step 4-7: Encoder layersfor j in range(self.num_encoder_layers):# Auto-CorrelationTj1 = self.encoder_layers[j].auto_correlation(Y_en) + Y_en# Feed ForwardTj2 = self.encoder_layers[j].feed_forward(Tj1) + Tj1Y_en = Tj2# Step 9: Embed decoder inputY_de = self.decoder_embedding(Y_des[:, :, None])C0_de = torch.zeros_like(Y_de)# Step 10-15: Decoder layersfor j in range(self.num_decoder_layers):# Auto-CorrelationTj1, Cj1 = self.decoder_layers[j].auto_correlation(Y_de) + Y_de# Cross AttentionTj2, Cj2 = self.decoder_layers[j].cross_attention(Tj1, Y_en) + Tj1# Feed ForwardTj3, Cj3 = self.decoder_layers[j].feed_forward(Tj2) + Tj2Y_de = Tj3C_de = Cj1 + Tj1 * Cj1 + Tj2 * Cj2 + Tj3 * Cj3# Step 16-17: Final outputY_pred = self.output_layer(Y_de)Y_pred = Y_pred.squeeze(-1) + C_dereturn Y_predclass AutoCorrelationLayer(nn.Module):def __init__(self, d_model, num_heads=8):super(AutoCorrelationLayer, self).__init__()self.d_model = d_modelself.num_heads = num_headsself.query_projection = nn.Linear(d_model, d_model)self.key_projection = nn.Linear(d_model, d_model)self.value_projection = nn.Linear(d_model, d_model)self.out_projection = nn.Linear(d_model, d_model)self.feed_forward = nn.Sequential(nn.Linear(d_model, d_model * 4),nn.ReLU(),nn.Linear(d_model * 4, d_model))def auto_correlation(self, x):batch_size, seq_len, _ = x.size()Q = self.query_projection(x)K = self.key_projection(x)V = self.value_projection(x)# Reshape for multi-head attentionQ = Q.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)K = K.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)V = V.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)# Scaled dot-product attentionscores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_model // self.num_heads)attention = torch.softmax(scores, dim=-1)out = torch.matmul(attention, V)out = out.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)out = self.out_projection(out)return outdef feed_forward(self, x):return self.feed_forward(x)class DecoderLayer(AutoCorrelationLayer):def __init__(self, d_model, num_heads=8):super(DecoderLayer, self).__init__(d_model, num_heads)self.cross_query = nn.Linear(d_model, d_model)self.cross_key = nn.Linear(d_model, d_model)self.cross_value = nn.Linear(d_model, d_model)self.cross_out = nn.Linear(d_model, d_model)def cross_attention(self, x, encoder_output):Q = self.cross_query(x)K = self.cross_key(encoder_output)V = self.cross_value(encoder_output)batch_size, seq_len, _ = x.size()Q = Q.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)K = K.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)V = V.view(batch_size, seq_len, self.num_heads, -1).transpose(1, 2)scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_model // self.num_heads)attention = torch.softmax(scores, dim=-1)out = torch.matmul(attention, V)out = out.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)out = self.cross_out(out)return out, attention# Example usage:
if __name__ == "__main__":input_length = 96num_encoder_layers = 2num_decoder_layers = 2model = SVDAutoformer(input_length, num_encoder_layers, num_decoder_layers)# Dummy input (batch_size, sequence_length)Y = torch.randn(32, input_length)output = model(Y)print(output.shape)  # Should be [32, 96]

总结

预测水质并及时采取行动至关重要。然而，传统的预测方法不能有效地捕捉时间序列中的时间相关性，并且容易受到噪声的干扰。文章所提出的SVD-自整定器结合了Savitzky-Golay滤波器、变分模式分解、自相关机制和改进的Transformer。其SG滤波和VMD能有效地降低噪声干扰，提取水质数据的非线性特征。此外，SVD-Autoformer利用深度分解架构和自相关机制。一方面，从水质数据中分解出更多的可预测成分。另一方面，实现了序列级链接，提高了信息利用率。